【05】方向梯度直方图（HOG）详解：从原理到实现

简介

方向梯度直方图（Histogram of Oriented Gradients, HOG）是计算机视觉领域经典的目标检测特征描述子，由法国研究员Dalal等人于2005年CVPR会议提出，最初用于解决行人检测问题。其核心思想可概括为：目标的局部形状与表象，能通过边缘/轮廓的梯度方向密度分布有效刻画——将图像划分为多个局部区域（cell），统计每个区域内像素的梯度方向直方图，再通过归一化与拼接形成全局特征向量。HOG因出色的形状描述能力，至今仍是目标检测、图像识别任务的基础工具之一。

算法流程：从像素到特征向量的五步拆解

HOG特征提取的核心逻辑是“局部梯度统计+归一化”，具体分为五大步骤（流程如图1）：

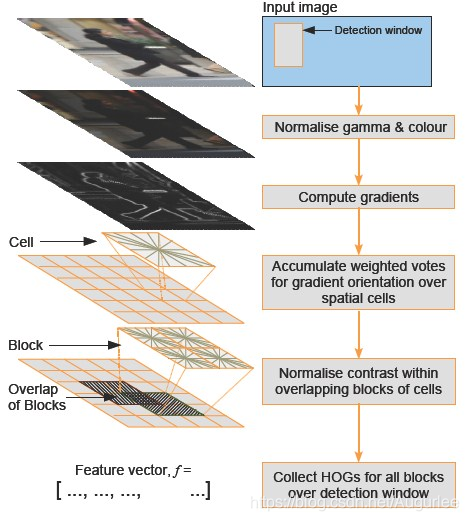
1. 灰度化与Gamma校正：抵消光照干扰

光照变化是计算机视觉的常见噪声（如阴影、过曝），HOG通过两步预处理降低其影响：

（1）灰度化

HOG聚焦梯度信息（边缘/轮廓的本质是梯度突变），而色彩对形状描述无贡献。将RGB图像转换为灰度图的公式为：$$Gray=0.3\times R+0.59\times G+0.11\times B$$（权重基于人眼对绿光更敏感的视觉特性，确保灰度图保留足够的形状信息。）

（2）Gamma校正

通过幂运算调整图像亮度，抵消局部光照不均。常用平方根法（$\gamma =0.5$），公式为：$$I^{\prime }(x,y)=I(x,y{)}^{\gamma }$$

• 当$\gamma <1$时，图像整体变暗，突出暗部细节；
• 当$\gamma >1$时，图像整体变亮，突出亮部细节。

2. 计算梯度：捕捉边缘的“强度与方向”

梯度是HOG的核心信息——它同时反映像素的“边缘强度”（梯度大小）与“边缘方向”（梯度方向）。HOG采用简单差分算子计算梯度：

• 水平梯度（$G_x$）：捕捉垂直边缘（如物体的左右轮廓），算子为$[-1,0,1]$（左像素减右像素）；
• 垂直梯度（$G_y$）：捕捉水平边缘（如物体的上下轮廓），算子为$[-1,0,1{]}^T$（上像素减下像素）。

对每个像素$(x,y)$，计算梯度大小$G$与方向角$\theta$：$$G=\sqrt{G_x^2+G_y^2}$$$$\theta =\arctan 2(G_y,G_x)$$（$\arctan 2$确保方向角范围为$[-\pi ,\pi ]$，对应0°~360°的物理方向。）

3. 统计cell的梯度方向直方图：局部形状的“直方图表达”

将灰度图划分为多个cell（如8×8像素的正方形区域），每个cell内的梯度方向被量化为 bins（通常9个，对应0°、20°、…、160°，每20°一个bin）。

对cell内每个像素，根据其梯度方向$\theta$归属到对应的bin，并将梯度大小$G$作为“权重”加到该bin的计数中。例如：

• 若某像素的梯度方向为30°，则加到“20°~40°”的bin中；
• 若梯度大小为5，则该bin的计数加5。

最终，每个cell生成一个长度为$nbins$（如9）的直方图向量，示例如图2：

【在此处插入cell梯度直方图示意图：8×8 cell的9-bin梯度方向分布】

4. Block块内归一化：消除光照强度的影响（重点）

cell直方图仍受光照强度干扰（如亮区域的梯度大小普遍更大），需通过Block归一化抵消这种差异。Block是由多个cell组成的重叠区域（如2×2 cell，即16×16像素），步长通常为1个cell（重叠率50%）。

对每个Block内的所有cell直方图向量拼接成的长向量$v$，采用L2归一化处理（最常用的方式）：$$v_{\text{norm}}=\frac{v}{\sqrt{\Vert v{\Vert }_2^2+ϵ}}$$（$ϵ=1e-5$，避免分母为0；$\Vert v{\Vert }_2$是向量的L2范数，即各元素平方和的平方根。）

归一化后的Block特征对光照变化更鲁棒，是HOG性能的关键保障——例如，同一物体在亮处与暗处的梯度大小不同，但归一化后的直方图形状一致。

5. 生成HOG特征：拼接所有Block的归一化向量

将图像中所有Block的归一化直方图向量按空间顺序拼接，形成最终的HOG特征向量。以64×128像素的行人图像为例：

• cell大小8×8 → 图像分为$64/8\times 128/8=8\times 16$个cell；
• Block大小2×2 cell → Block数量为$(8-1)\times (16-1)=7\times 15$（步长1 cell）；
• 每个Block特征长度为$2\times 2\times 9=36$ → 总特征长度为$7\times 15\times 36=3780$。

HOG特征的优缺点：适合什么场景？

HOG的设计逻辑决定了它的优势与局限，需根据任务场景选择：

优点

1. 形状刻画精准：直接以梯度方向分布描述目标局部形状，契合边缘/轮廓的视觉本质；
2. 抗干扰能力强：位置与方向量化抑制小范围平移/旋转，局部归一化抵消光照变化；
3. 维度合理：忽略色彩信息，特征维度远低于原始图像（如64×128图像仅3780维）；
4. 局部关系保留：分块分cell的结构，保留了像素间的局部空间关系（如“眼睛在鼻子上方”的位置信息）。

缺点

1. 实时性差：多步骤流程（尤其Block归一化）导致特征生成速度慢，难用于实时检测；
2. 遮挡敏感：依赖完整的局部梯度分布，遮挡会破坏直方图的连续性（如行人被遮挡后，HOG特征无法完整描述人体形状）；
3. 噪点敏感：梯度对孤立噪点的响应强，易干扰直方图统计（如椒盐噪声会产生虚假梯度）；
4. 无颜色信息：仅用灰度图，丢失颜色带来的目标区分度（如红色汽车与蓝色汽车的HOG特征可能相似）。

OpenCV实现HOG特征提取：从理论到代码

OpenCV提供cv2.HOGDescriptor类，封装了HOG特征提取的所有步骤，只需设置关键参数即可快速使用。

关键参数说明

参数	含义	常用值
`winSize`	检测窗口大小（需与训练数据一致）	(64, 128)
`blockSize`	Block大小（需是cellSize的整数倍）	(16, 16)
`blockStride`	Block步长（重叠率=1 - 步长/blockSize）	(8, 8)
`cellSize`	cell大小	(8, 8)
`nbins`	梯度方向 bins 数量	9

代码示例：提取行人图像的HOG特征

import cv2
import numpy as np# 1. 读取并预处理图像（转为灰度图+ resize到检测窗口大小）
img = cv2.imread('pedestrian.jpg', 0)  # 0表示灰度模式
img_resized = cv2.resize(img, (64, 128))  # 调整为64×128像素# 2. 初始化HOG描述符
hog = cv2.HOGDescriptor(winSize=(64, 128),    # 检测窗口大小blockSize=(16, 16),   # Block大小（2×2 cell）blockStride=(8, 8),   # Block步长（重叠50%）cellSize=(8, 8),      # cell大小nbins=9               # 9个梯度方向bin
)# 3. 计算HOG特征
hog_features = hog.compute(img_resized)# 输出特征维度（64×128图像的HOG特征长度为3780）
print("HOG特征维度：", hog_features.shape)  # 输出：(3780, 1)

总结

HOG是**“用局部梯度分布描述形状”**的经典方法，其核心优势在于“聚焦形状本质+抗光照干扰”。尽管深度学习时代（如YOLO、Faster R-CNN）的特征提取能力更强，但HOG的思想仍值得学习——它揭示了计算机视觉的本质：从像素中提取“有意义的统计信息”。

无论是行人检测、车牌识别还是物体分类，HOG都是理解“特征提取”的重要起点。结合SVM分类器，HOG曾是行人检测的“黄金组合”；即使在今天，HOG仍可作为传统计算机视觉方法的基准，帮助我们理解深度学习特征的底层逻辑。