当前位置：首页 > news >正文

【计算几何 | 那忘算 11】旋转卡壳（附详细证明）

news 2025/11/13 9:57:55

专栏：再来一遍一定记住的算法_proMatheus的博客-CSDN博客

前置知识：

凸多边形的直径：凸多边形上任意两点间距离的最大值。

对踵（zhǒng）点对：如果过凸包上的两个点可以画一对平行直线，使凸包上的所有点都夹在两条平行线之间或落在平行线上，那么这两个点叫做一对对踵点。

由于代码中需要大量向量辅助计算，不了解的话建议你先看这个。

0.前导

旋转卡壳算法是解决一些与凸包（给定点集的最小凸多边形）有关问题的高效算法，

计算时就像一对平行直线卡壳卡住凸包旋转而得名。

模板题：P1452 【模板】旋转卡壳 / [USACO03FALL] Beauty Contest G - 洛谷 (luogu.com.cn)

旋转卡壳的精髓，就是利用凸多边形的直径一定在对踵点处取得的特性，

以及一个凸多边形中对踵点最多只有 3n / 2 对的性质（n 和下文的 N 都指多边形的点数），

来将原来 $O(N^2)$ 的枚举点对求凸多边形直径，

优化成双指针单调移动的 $O(N)$ 算法。

1.算法流程

首先题目给了 n 个点，想求凸包直径。

我们就先求出凸包（用 Andrew 单调链算法，后面会细讲，这里先假设已经求出来了）。

接着我们了解定理（后面会证明，先记着）：凸多边形的直径一定在对踵点处取得。

又知道对踵点的定义：

过两个对踵点画两条平行直线，那凸包上的所有点都夹在两条平行线之间或落在平行线上。

就先假设其中的一条直线是多边形的一条边 E，为了另一条平行直线也能 “括住” 所有点，

我们就寻找离边 E 垂直距离最远的点，过点作一条与边 E 相平行的直线。

这样满足对踵点的定义，使凸包上的所有点都夹在两条平行线之间或落在平行线上。

（因为垂直距离最远的点能 “括住” 的范围最大，并且因为是凸多边形，所以满足要求）

如图，确定边 AB，求出离 AB 垂直距离最远的点 E。

点对 {A,E} 和 {B,E} 都满足对踵点要求，也就都有可能成为多边形直径。

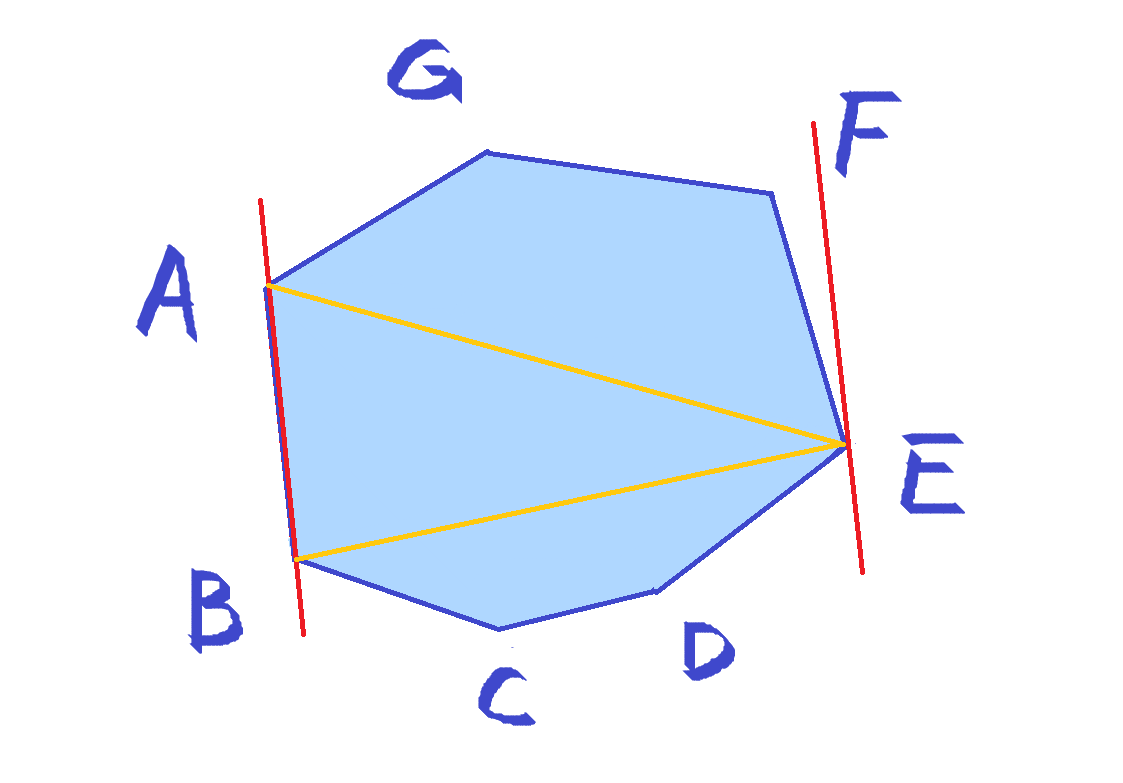
然后我们想要逆时针枚举边，即下一条边是 BC，同样找出离 BC 垂直距离最远的点。

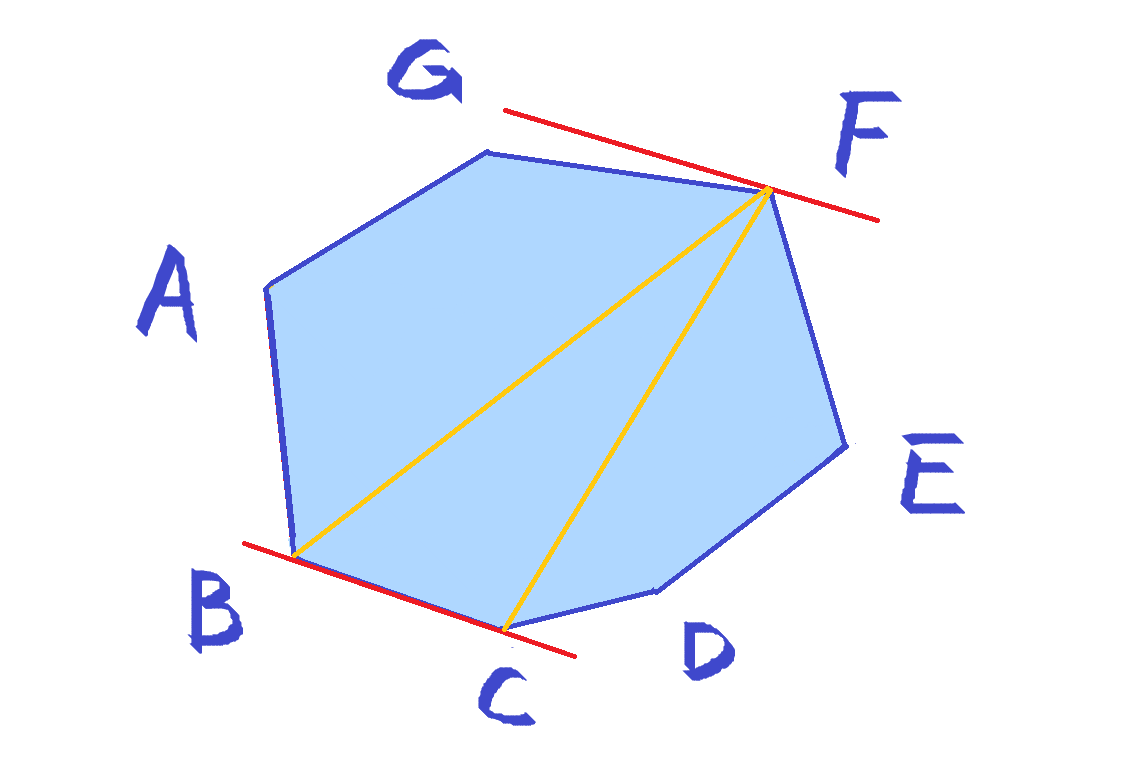
（点对 {B,F} 和 {C,F} 都满足对踵点要求，也就都有可能成为多边形直径）

发现距离最远的点变成了 F，即 AB -> BC，E -> F，边和点都同样逆时针旋转。

因为多边形是凸的，所以我们大胆猜测一下：距离最远点是单调移动的（不会顺时针 “后退”）。

那么可以双指针一个枚举边一个枚举点，点的指针随着边的指针移动。

又因为枚举出来的对踵点最多只有 3n / 2 对，所以时间复杂度是 $O(N)$ 的。

好像是做完了？但其实还有几个疑问：

（1）为什么凸多边形的直径只能在对踵点处取得？

（2）为什么距离最远点一定是单调移动的？

（3）为什么对踵点最多只有 3n / 2 对？

我们一个一个解决。

1.1 为什么凸多边形的直径只能在对踵点处取得

还是之前那个多边形，不过被我小小改了下：

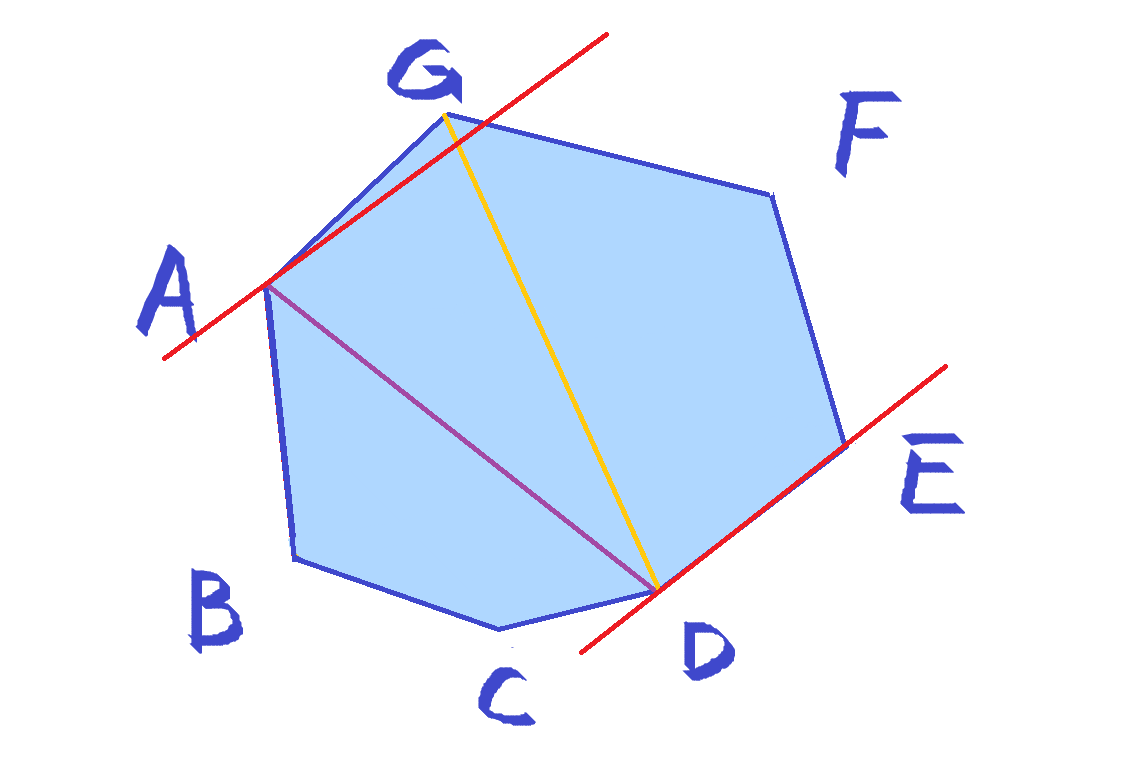
假设直径是 AD，但很明显 {A,D} 不是对踵点。

那应该怎么证明真正的对踵点 {G,D} 连成的线段 GD 长度比 AD 长？

首先根据余弦定理：

对于任意三角形，有： $a^2=b^2+c^2+2bc\ cos\ \angle A$

当 $0<\angle A<90^{\circ}$ ， $cos\ \angle A>0$ ，有 $a^2<b^2+c^2$ 。

当 $\angle A=90^{\circ}$ ， $cos\ \angle A=0$ ，有 $a^2=b^2+c^2$ 。

当 $90^{\circ}<\angle A<180^{\circ}$ ， $cos\ \angle A<0$ ，有 $a^2>b^2+c^2$ 。

当 $\angle GAD\geq 90^{\circ}$ 时， $AG^2+AD^2\leq GD^2$ ，GD 长度绝对大于 AD。

而 $\angle GAD<90^{\circ}$ 的情况，即 $AG^2+AD^2> GD^2$ ，好像并不能判断。

这时过 D 点作垂直 AG 与点 H：

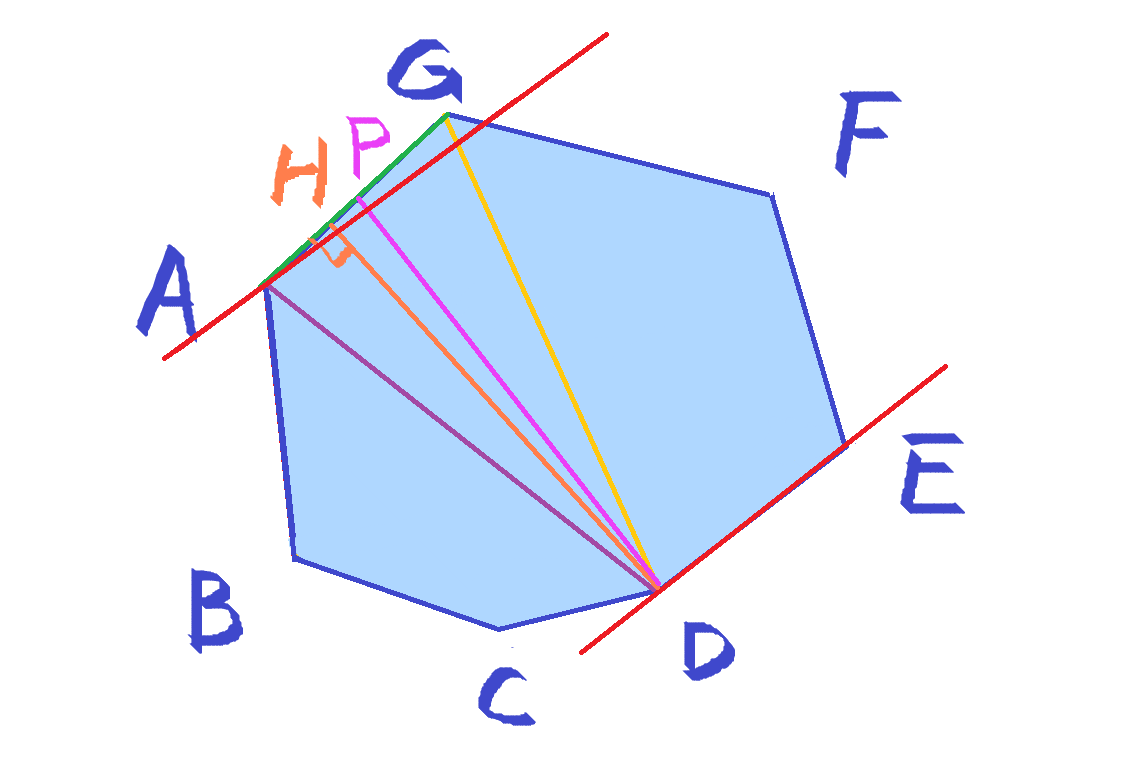
由于 {A,D} 不是对踵点，点 H 一定在 AG 偏点 A 那侧，即 AG 中点 P 的左侧。

（这里可以感性理解为 {A, D} 不是对踵点的原因是：在 ADG 这个锐角三角形中）

（D 点在偏向 A 点的那一侧，让 G 点能离的更远，更有可能当对踵点）

（可以自己尝试画几个图，在固定 AD 的情况下改变 AG 的角度）

因为 $AH>HG$ ， $AH^2+HD^2=AD^2$ ， $HG^2+HD^2=GD^2$ 。

所以 $AD<GD$ 。

这保证了整个算法的基础理论。

1.2 为什么距离最远点一定是单调移动的 & 3n / 2

（2）和（3）可以一起讲。

想象用两块平行木板夹住凸多边形旋转。固定左木板在顶点 A，右木板会接触对面的某个位置。

当左木板从 A 转到逆时针邻顶点 B 时，右木板的接触点只能向前移动，不能后退（凸性决定）。

在 A 到 B 的旋转过程中，右木板最多经历三种状态：

接触一个顶点 C（形成 A - C 对）
接触一条边 CD（此时 A 同时与 C、D 构成对踵对，因为木板可以贴着整条边）
再接触下一个顶点 E

所以每个顶点最多产生 3 个对踵关系。

n 个顶点共 3n 个，但每对 (A,C) 被计算了两次（A 找 C 和 C 找 A），所以总数不超过 3n / 2。

关键在于凸性保证了接触点只能单调移动，同时保证只有 3n / 2 个点对，

保证时间复杂度 $O(N)$ （可能还得乘个常数级但差不了多少）。

2.代码

可以先返回我开头给的那个链接学习叉积的作用。

代码在最后面！

Andrew 算法中维护栈（建议结合代码看）

维护下凸壳时，要求新的节点在 top 的前面的左边（new 1）。

那么就从 top - 1 连到 new，看看是否在向量 top - 1 连到 top 的左边。

这里直接计算两条向量的的叉积，看是否小于等于 0（右手定则），如果是就把 top 踢掉。

反之不踢，放到栈里。

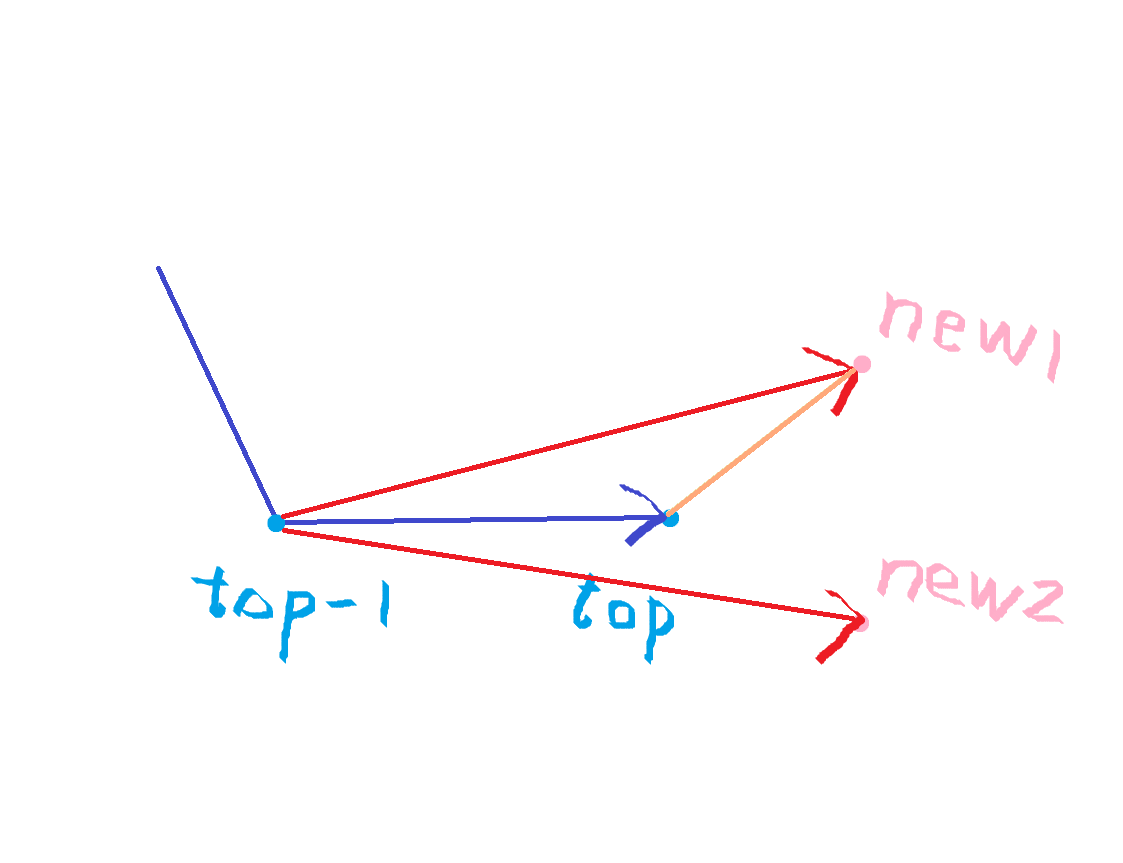
维护上凸壳时，要求新的节点在 top 的后面的左边（new 2）。

那么就从 top - 1 连到 new，看看是否在向量 top - 1 连到 top 的左边。

这里直接计算两条向量的的叉积，看是否小于等于 0（右手定则），就把 top 踢掉。

反之不踢，放到栈里。

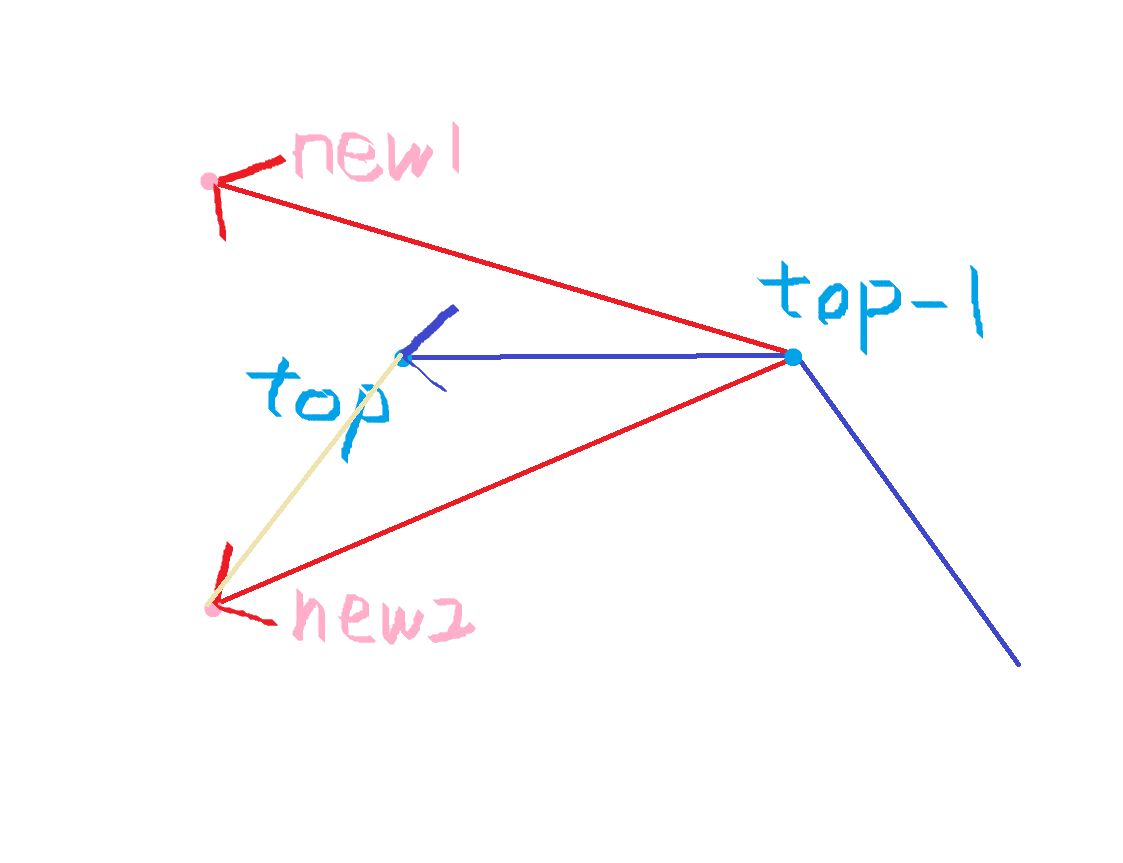
Rotating Calipers 旋转卡壳算法中比较距离（建议结合代码看）

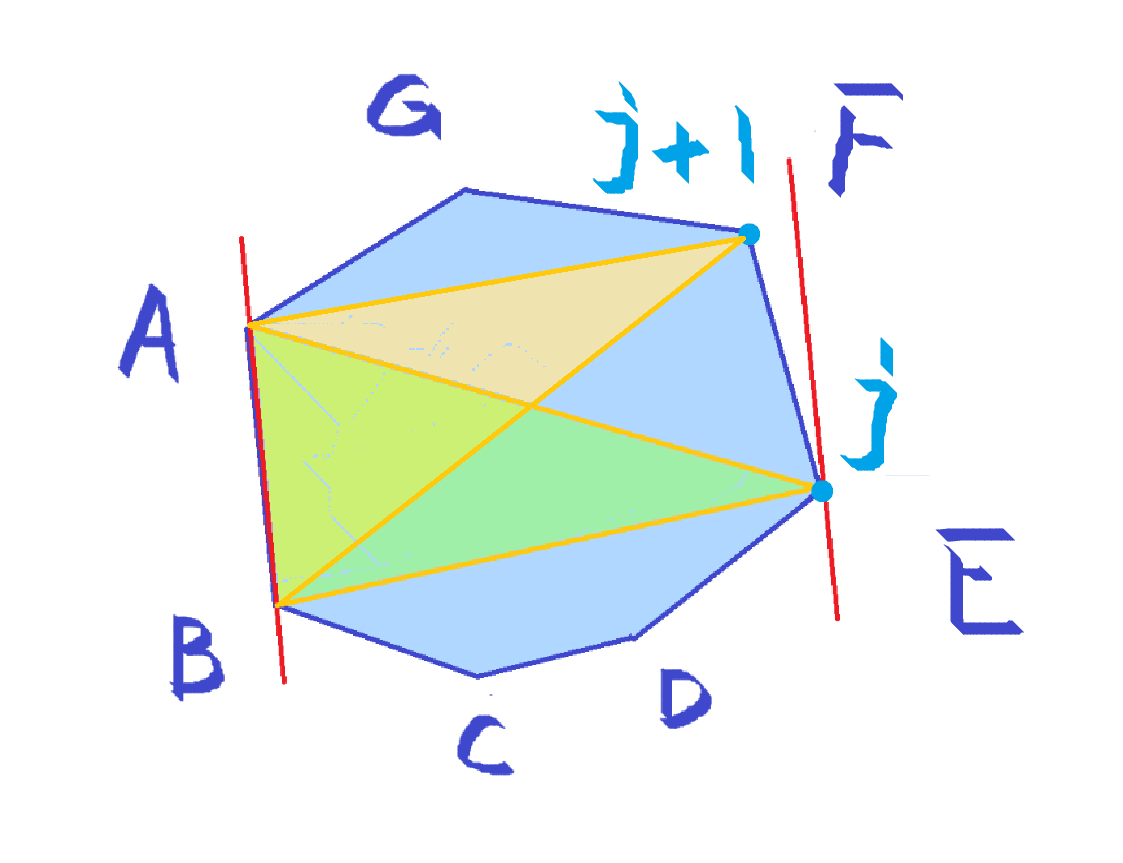
如上图，指针 j 是最远距离点的指针。

每次比较三角形 AFB 和三角形 AEB 的面积，因为俩三角形同底，所以面积大的那个高就大。

然后尝试用 AE 和 BE 更新直径。

（求三角形的面积用的也是叉积，比如说求 ABE 就是 $\vec{AB}*\vec{AE}$ 叉乘出来的）

注释代码

求凸包时间复杂度是 $O(Nlog\ N)$ （瓶颈是排序），旋转卡壳是 $O(N)$ 。

#include<bits/stdc++.h>
using namespace std;const int N = 5e4 + 10;int n, top;   // P：输入点集, sta：凸包点集
struct Point {double x, y;
} P[N], sta[N];   // n：点数, top：凸包栈顶指针Point operator-(Point na, Point nb) {return {na.x - nb.x, na.y - nb.y};
}bool operator<(Point na, Point nb) {   // 从小到大排序：第一关键字 x，第二关键字 y if (na.x != nb.x) {return na.x < nb.x;}return na.y < nb.y;
}double operator*(Point na, Point nb) {   // 叉积 return na.x * nb.y - na.y * nb.x;
}double dis(Point a, Point b) {Point c = a - b;return c.x * c.x + c.y * c.y;
}void Andrew() {   // 安卓算法（apple？ sort(P + 1, P + n + 1);top = 0;    // 清空栈// x 从左到右构建下凸壳，每一条边都要在前一条边的左边 for (int i = 1; i <= n; i ++) {// 维护栈的凸性：如果新点与栈顶两点构成非左转（右转或共线），弹出栈顶while (top > 1 && (sta[top] - sta[top - 1])* (P[i] - sta[top - 1]) <= 0) {top --;}top ++;sta[top] = P[i];} int t = top;    // 保存下凸壳终点位置// x 从右到左构建上凸壳，每一条边都要在前一条边的左边 for (int i = n - 1; i >= 1; i --) {// *注意！这里从 n - 1 开始遍历 // 因为求下凸壳时，最右点一定是 P[n]，这里要拐回去往左边求上凸壳// 为了不重复，从 n - 1 开始 // 维护栈的凸性：如果新点与栈顶两点构成非左转（右转或共线），弹出栈顶while (top > t && (sta[top] - sta[top - 1])* (P[i] - sta[top - 1]) <= 0) {top --;}top ++;sta[top] = P[i];}  n = top - 1; // 更新 n 为凸包顶点数（首尾点重复，减 1）
}double RC() {    // 旋转卡壳算法求凸包直径（最远点对距离平方）double res = 0;for (int i = 1, j = 2; i <= n; i ++) {    // i：当前边起点, j：对踵点// 寻找 i -> i + 1 边的对踵点：比较相邻点到边的距离，用叉积计算出同底三角形面积后比较 // 当 j + 1 到边 i -> i + 1 的距离大于 j 到该边的距离时，j 向前移动while ((sta[i + 1] - sta[i]) * (sta[j] - sta[i]) < (sta[i + 1] - sta[i]) * (sta[j + 1] - sta[i])) {j = j % n + 1; // 循环处理（j 到达末尾时回到开头）}// 更新最远距离：比较当前边的两个端点到对踵点j的距离res = max(res, max(dis(sta[i], sta[j]), dis(sta[i + 1], sta[j])));}return res;
}int main () {ios::sync_with_stdio(false);cin.tie(0);cin >> n;for (int i = 1; i <= n; i ++) {cin >> P[i].x >> P[i].y;}Andrew();     // 构建凸包cout << fixed << setprecision(0) << RC() << "\n";return 0; 
}