变分自编码器VAE
VAE是什么
VAE是一种生成模型。它的目标是学习训练数据(比如人脸图片)的潜在分布,然后从这个分布中采样,生成新的、类似但又不完全相同的数据。
你可以把它想象成一个“智能的压缩与再造”系统:
编码器(Encoder):接收一张输入图片(例如,数字“2”的手写图片),不是将其压缩成传统的字节码,而是压缩成两个向量:一个表示均值(μ),一个表示标准差(σ)。这组(μ, σ)定义了一个概率分布(通常是高斯分布)。我们可以认为,这个分布代表了“所有可能的数字‘2’的抽象特征”。
潜在空间(Latent Space):这是一个比原始数据维度低得多的空间。上面的(μ, σ)就是在这个空间里定义了一个分布。关键一步:VAE从这个分布中随机采样一个点 z。这个随机性正是生成多样性的来源。
解码器(Decoder):将采样得到的潜在点 z 作为输入,尝试将其重建回原始的图片尺寸,输出一张生成的图片。
如果只有重建任务,模型可能会“作弊”——它可能让编码器学会把每个输入图片都编码成潜在空间里一个互不重叠的、孤立的点(即标准差σ趋近于0)。这样解码器就能完美重建。但这样做的后果是,潜在空间是不连续的、没有结构。当我们从两个“2”的编码点之间采样时,解码出来的可能是一团乱码,无法实现真正的“生成”。
KL散度
KL散度,全称Kullback-Leibler Divergence,中文常译作“相对熵”。它是一个衡量两个概率分布之间差异的工具。
假设有两个分布 P 和 Q。KL散度 KL(P || Q) 衡量的是:当我们用分布 Q 来近似真实分布 P 时,所损失的信息量。
如果 P 和 Q 的形状完全一样,那么 KL(P || Q) = 0。
如果 P 和 Q 的形状差异越大,KL(P || Q) 的值就越大。
重要性质:KL散度是非对称的,即 KL(P || Q) ≠ KL(Q || P)。它衡量的是从 P 到 Q 的“方向性”信息损失。
在VAE中的具体角色
在VAE中,我们希望潜在空间是有规律的、连续的、平滑的。一个理想的状态是,所有输入图片编码后的潜在分布都趋近于一个简单的标准正态分布 N(0, 1)。
为什么?
如果所有编码分布都像 N(0, 1),那么潜在空间就会充满整个区域,而不是挤在几个孤立的点上。
由于所有分布都类似于 N(0, 1),它们之间会有重叠,空间是连续的。
这样,我们就可以放心地从 N(0, 1) 中任意采样,并相信解码器能生成一个有意义的输出。
因此,在VAE的损失函数中,KL散度的作用就是:
计算编码器为每个输入产生的分布 Q(z|X)(由μ和σ定义)与标准正态分布 P(z) = N(0, 1) 之间的差异,并最小化这个差异。
VAE的损失函数——两大组成部分
VAE的总损失函数是两项的加权和:
损失 = 重建损失 + KL散度损失
-
重建损失(Reconstruction Loss)
目的:确保解码器生成的图片与原始输入图片尽可能相似。
实现:对于输入图片 X 和重建图片 X’,通常使用:
二元交叉熵(Binary Cross-Entropy):如果像素值在 [0, 1] 之间。
均方误差(MSE):(X - X‘)² 的平均值。
作用:驱使模型保留输入数据的关键信息。 -
KL散度损失(KL Divergence Loss)
目的:规范潜在空间,使其逼近标准正态分布。
公式:对于由一个输入数据产生的分布 N(μ, σ²) 和标准正态分布 N(0, 1),其KL散度有一个漂亮的解析解:
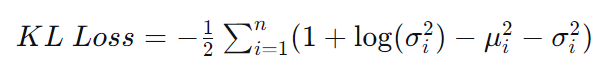
这里的 n 是潜在空间的维度,μ_i 和 σ_i 是第 i 维的均值和标准差。
两者的平衡
如果只强调重建损失,模型会忽略潜在空间的结构,导致过拟合,生成能力差。
如果只强调KL散度损失,模型会强迫所有潜在分布都变成 N(0, 1),而完全忽略输入数据,导致重建效果极差(“后验坍塌”现象)。
VAE通过同时优化这两项,找到一个平衡点:既能让重建图片尽可能像原图,又能让潜在空间规整有序。
其它:
为什么只有重建任务,模型可能会“作弊”——它可能让编码器学会把每个输入图片都编码成潜在空间里一个互不重叠的、孤立的点(即标准差σ趋近于0)。
核心思想:没有KL散度,模型会选择“最轻松”的路径
想象一下,你是一位老师,给学生(模型)布置了一项任务:
“记住这100个复杂的数学公式(训练数据),然后我随时抽查,你要能默写出来。”
场景一:只有“重建损失”(没有KL散度)
学生的目标只有一个:在抽查时,默写得和原公式一字不差。
最聪明的“作弊”策略是什么?
学生会给每个公式分配一个独一无二的、极其简短的暗号。
比如,第1个公式的暗号是 A,第2个是 B,……,第100个是 #。
当老师抽查第1个公式时,学生看到暗号 A,就在脑海里调出对应的完整公式,然后默写出来。结果完全正确,重建损失为0!
这对应到VAE中:
编码器:学会了将每张输入图片(如数字“2”的图片A)映射到潜在空间一个确定的点(比如点 (0, 0, 0))。为了确保万无一失,它会让这个点的方差(σ)无限趋近于0。这意味着:“看到图片A,必须且只能输出点 (0,0,0),没有任何随机性。”
解码器:学会了看到潜在空间的点 (0,0,0),就必须且只能输出图片A。
结果:
重建效果极好:因为是一对一的精确映射,输入什么就能完美重建什么。
潜在空间结构:100张图片,在潜在空间就是100个孤立的、互不联系的“针尖”一样的点。点与点之间是巨大的空白和无效区域。
为什么这是灾难性的?
现在,老师(我们)想测试学生的真正理解能力(生成能力),说:“不要默写我教过的了,请你自己创造一个新公式。”
学生傻了。因为他只知道 A, B, …, # 这100个暗号。你让他从 A 和 B 中间取一个暗号,比如 A.5,他完全不知道这是什么意思,只能胡乱写一通。生成的结果是一团糟。
在VAE中,这就是“无法生成新数据”。 我们从潜在空间的两个有效点之间采样,解码器根本没见过这种输入,输出自然是无意义的噪声。
场景二:加入“KL散度损失”
现在,老师改变了任务要求:
“你不仅要能默写公式,而且你用的暗号必须符合我给你的‘暗号规则手册’(标准正态分布)。我会根据你的暗号是否符合规则来扣分。”
这个“暗号规则手册”规定:暗号不能是固定的几个点,而应该是在一个连续的、以0为中心的范围内随机生成。
学生的新策略是什么?
他不能再使用固定的暗号 A, B了。他必须学会“概括”和“归纳”。
他看到第1个公式(比如是勾股定理 a²+b²=c²),他需要用一个符合“规则手册”的暗号来表示它,比如 (主题=几何,变量=3,次数=2)。
他看到第2个公式(比如是球体体积公式 V=4/3πr³),他用另一个符合规则的暗号表示,比如 (主题=几何,变量=1,次数=3)。
KL散度损失 就像老师在检查他的暗号是否真的在遵循规则手册。如果他试图把某个公式的暗号固定成一个特殊值,就会被扣分。
这对应到VAE中:
编码器:被迫为每张输入图片输出一个分布(而不是一个点)。比如,对于数字“2”的图片,它可能输出一个以 μ_2 为中心,σ_2 为方差的高斯分布。这个分布必须与标准正态分布 N(0,1) 相似。
采样:我们从“数字2的分布”里采样,每次得到的点都略有不同,但都围绕着 μ_2。
解码器:它被训练得要能够将所有围绕 μ_2 的点都解码成看起来像“2”的图片。这就迫使解码器学习到“2”的本质特征(比如有个圈,下面一条横线),而不是去记忆某一张具体的图片。
结果:
重建效果稍差:因为引入了随机性,重建的图片可能不如场景一那么完美像素级复现,但依然很像。
潜在空间结构:所有“2”的编码分布聚集在一起,所有“3”的聚集在一起,并且这些分布都彼此重叠,整个空间被有效点填满,形成一个连续、平滑的流形。
强大的生成能力:现在,我们从标准正态分布中任意采样一个点 z,这个点很可能落在某个数字的分布范围内,或者落在两个分布的交界处。解码器因为见过它“邻居”的样子,能够合理地推断出这个新点 z 应该长什么样,从而生成一个新颖且合理的数字图片。
