INT303 Big Data Analysis 大数据分析 Pt.8 聚类

1. 聚类概述

聚类（Clustering）是数据分析中的一种方法，用于将数据集中的对象分组。这些对象在某些特征或属性上具有相似性，因此可以被归为一类。聚类的目标是识别数据中的自然分组或模式，以便更好地理解数据的结构和内在关系。

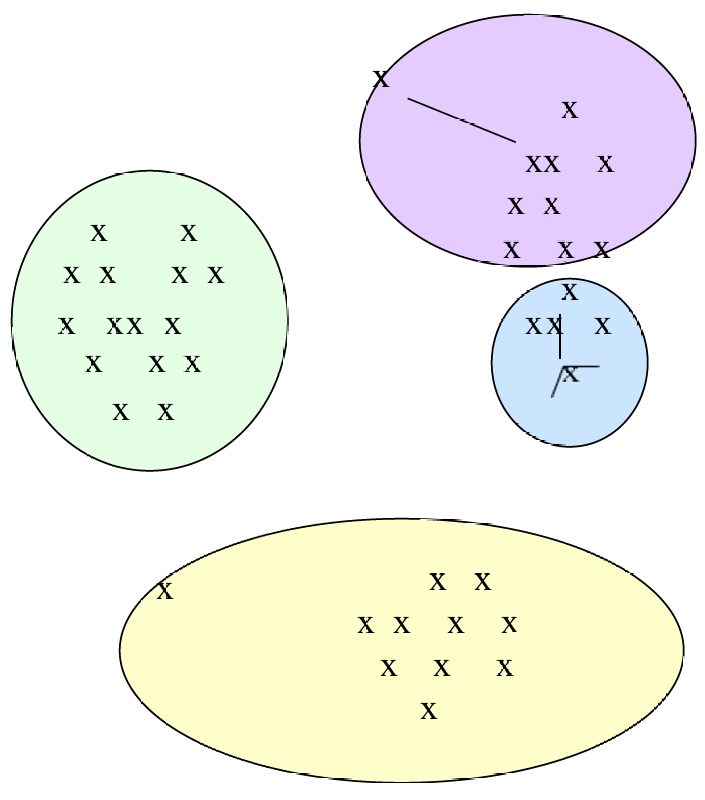
例如我们使用聚类理解下图数据的结构。

聚类问题涉及给定一组点（数据对象），这些点之间存在某种距离度量。
目标是将这些点分成若干个聚类（clusters），使得：
同一聚类中的成员彼此之间“接近”或“相似”。
不同聚类中的成员彼此“不接近”或“不相似”。

在聚类过程中，通常需要定义一个距离度量来衡量点之间的相似性或不相似性。
常用的距离度量包括：
欧几里得距离（Euclidean distance）：最常用的距离度量，计算两点之间的直线距离。
余弦距离（Cosine distance）：衡量两个向量之间的角度，常用于文本数据。
Jaccard距离：衡量两个集合的相似性，常用于二进制数据。
编辑距离（Edit distance）：衡量将一个字符串转换为另一个字符串所需的最少编辑操作次数，如插入、删除或替换字符。

我们不会把所有点都放进聚类中，聚类分析中同样存在异常值，如下图所示。

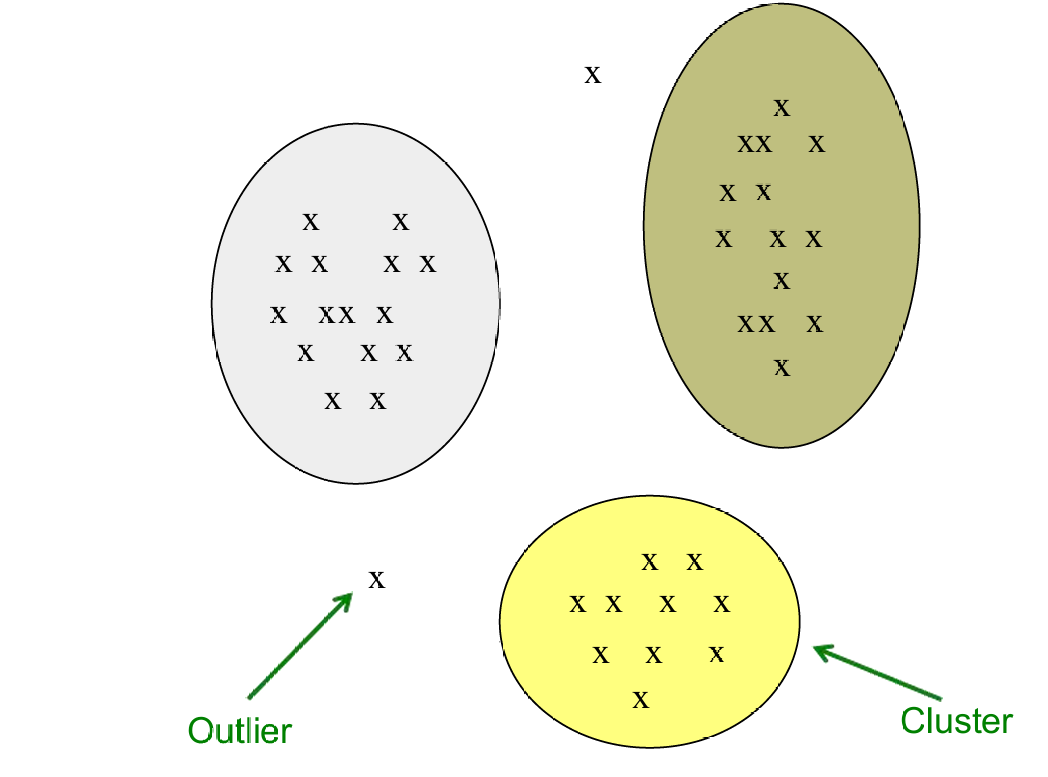
图中有三个不同颜色的椭圆形区域，每个区域代表一个聚类。
远离任何聚类的点就是异常值（Outliers）。

在二维空间中进行聚类分析看起来相对容易，因为人类可以直观地观察和理解二维图形。当处理的数据量较小时，聚类分析看起来也相对简单，因为可以手动检查和分类每个数据点。
但聚类问题通常处理的是高维空间中的数据点。高维数据可能包含数百或数千个特征。
因此在这些高维空间中，数据点之间的距离计算和聚类变得更加复杂。而且高维空间中的数据点看起来非常不同：几乎所有的数据点对之间的距离大致相同。（称为“维度的诅咒”），这意味着随着维度的增加，数据的可分性降低，聚类变得更加困难。
此外，高维空间中的数据点可能非常稀疏，使得聚类变得更加困难。

聚类问题包括

1. 对星系进行聚类分析。
   斯隆数字巡天（Sloan Digital Sky Survey），这是一个大型天文项目，它提供了一份包含20亿个“天体”（sky objects）的目录。这些天体根据它们在7个维度（频率带）上的辐射来表示。这些维度可能包括不同的光谱带，如紫外线、可见光、红外线等。
   面临的挑战是将这些天体聚类成相似的对象，例如星系、邻近的恒星、类星体等。这涉及到在高维空间中识别和分组相似的数据点。
   
2. 对音乐CD进行聚类分析。
   音乐通常可以根据不同的风格或类型进行分类，例如摇滚、流行、古典等。
   顾客在购买音乐CD时往往有偏好，他们可能倾向于购买某些特定的音乐类别。
   问题的核心是确定音乐CD的真正类别。尽管我们直观上知道音乐可以分成不同的类别，但这些类别具体是什么，以及如何定义这些类别，可能并不明确。
   每个音乐CD可以由购买它的顾客集合来表示。这意味着，如果两个CD被相似的顾客群体购买，那么这两个CD在某种程度上是相似的。
   如果两个CD有相似的顾客群体，那么这两个CD在顾客偏好上是相似的。反之，如果两个CD的顾客群体差异很大，那么这两个CD在顾客偏好上是不相似的。
   通过聚类分析，可以将音乐CD分成不同的类别，这有助于理解顾客的偏好，以及音乐的市场细分，帮助音乐商店或在线音乐平台更好地组织和推荐音乐。
   想象一个空间，其中每个维度代表一个顾客。在这个空间中，每个维度的值只有0或1，表示顾客是否购买了特定的CD。
   一个CD在这个空间中表示为一个点，其坐标$(x_1,x_2,...,x_k)$，其中$x_i=1$当且仅当第$i$个顾客购买了该CD时。
   对于像亚马逊这样的大型在线零售商，顾客的数量可能达到数百万甚至更多。因此，表示所有CD的这个空间的维度可能达到数百万级别。
3. 对文档进行聚类分析。
   每个文档被表示为一个向量$(x_1,x_2,...,x_k)$，其中$x_i=1$当且仅当第$i$个词（在某个顺序中）出现在文档中。这意味着每个词在文档中出现时，相应的维度值为1，否则为0。
   尽管理论上维度$k$可以是无限的，因为我们不限制词汇表的大小，但实际上在实践中，我们通常会选择一个有限的词汇表来表示文档。
   任务是找到具有相似词汇集的文档。这意味着如果两个文档包含相似的词集，它们可能讨论相同的主题。
   通过聚类分析，可以将文档分组到相关的主题中。这对于文本挖掘、信息检索、推荐系统等应用非常有用。
   我们前面说可以使用Jaccard距离、欧几里得距离（Euclidean distance）和余弦距离（Cosine distance）衡量点之间的相似性或不相似性，在这个例子中。

• 文档 = 词集（Document = set of words）
  当文档被视为一个词集时，可以使用Jaccard距离来度量文档之间的相似性。
  Jaccard距离计算两个集合交集大小与并集大小的比例，从而衡量文档的相似度。
• 文档 = 词空间中的点（Document = point in space of words）
  当文档被视为词空间中的一个点时，可以使用欧几里得距离来度量文档之间的距离。
  每个文档表示为一个向量$(x_1,x_2,...,x_N)$，其中$x_i=1$当且仅当第$i$个词出现在文档中。
  欧几里得距离计算两个点之间的直线距离。
• 文档 = 词空间中的向量（Document = vector in space of words）
  当文档被视为词空间中的一个向量时，可以使用余弦距离来度量文档之间的相似性。
  每个文档表示为从原点到$(x_1,x_2,...,x_N)$的向量。
  余弦距离基于向量之间的角度来度量相似性，常用于文本分析中，因为它考虑了向量的方向而不仅仅是大小。

聚类方法分为层次聚类和点分配。

1. 层次聚类（Hierarchical Clustering）
   凝聚型（Agglomerative，自底向上）：
   初始时，每个数据点都被视为一个单独的聚类。
   然后，算法反复将两个“最近”的聚类合并为一个聚类，直到所有点合并为一个聚类或达到某个停止条件。
   这种方法从底层开始，逐步向上构建聚类层次结构。
   分裂型（Divisive，自顶向下）：
   初始时，所有数据点被视为一个大聚类。
   然后，算法递归地将这个聚类分裂为更小的聚类，直到每个点成为一个单独的聚类或达到某个停止条件。
   这种方法从顶层开始，逐步向下构建聚类层次结构。
2. 点分配聚类（Point Assignment）
   这种方法涉及维护一组聚类，并将每个数据点分配到最近的聚类中。
   每个数据点根据其与各个聚类中心的距离被分配到最近的聚类中。

2. 层次聚类（Hierarchical clustering）

我们前面说了层次聚类分两种：

1. 凝聚型（Agglomerative，自底向上）：
   初始时，每个数据点都被视为一个单独的聚类。
   然后，算法反复将两个“最近”的聚类合并为一个聚类，直到所有点合并为一个聚类或达到某个停止条件。
   这种方法从底层开始，逐步向上构建聚类层次结构。
2. 分裂型（Divisive，自顶向下）：
   初始时，所有数据点被视为一个大聚类。
   然后，算法递归地将这个聚类分裂为更小的聚类，直到每个点成为一个单独的聚类或达到某个停止条件。

2.1 凝聚型（Agglomerative，自底向上）

我们这次主要学习聚集型，另一种分类型其实思想上是一样的。
凝聚型（Agglomerative）聚类方法的关键操作是重复合并两个最近的聚类。通过重复地合并最相似的两个聚类来构建聚类层次结构。

2.1.1 如何表示一个包含多个点的聚类？

当聚类合并时，如何表示每个聚类的位置以确定哪对聚类是最接近的，这是一个关键问题。
在欧几里得空间中，每个聚类可以由其质心（centroid）来表示，质心是聚类中所有数据点的平均值。

2.1.2 如何确定聚类的“接近度”？

确定聚类之间的接近度通常涉及到测量质心之间的距离。
质心之间的距离可以作为聚类距离的度量，用于决定哪两个聚类应该合并。
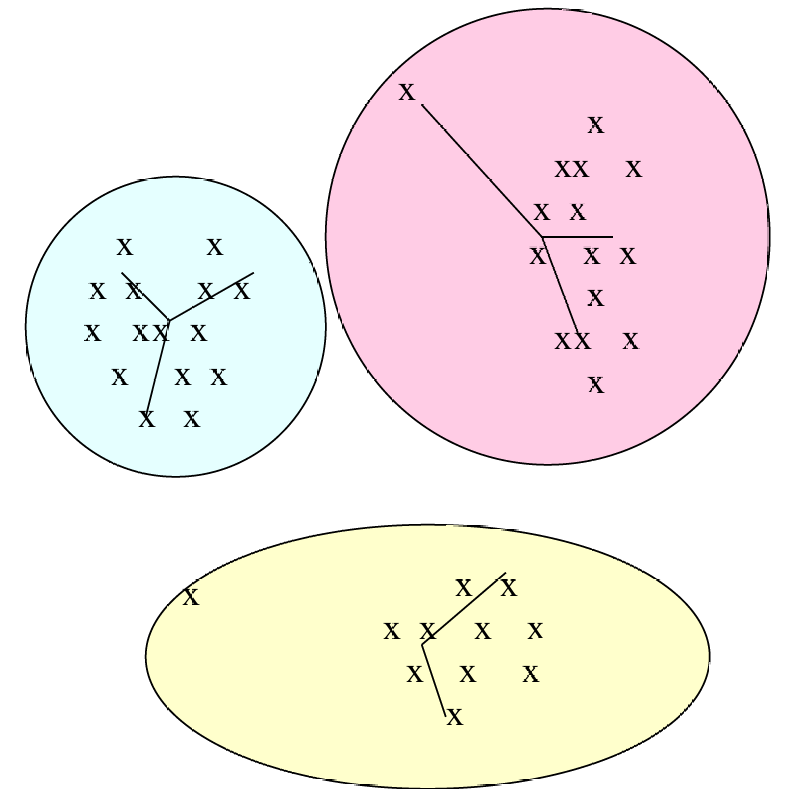
如下图所示。

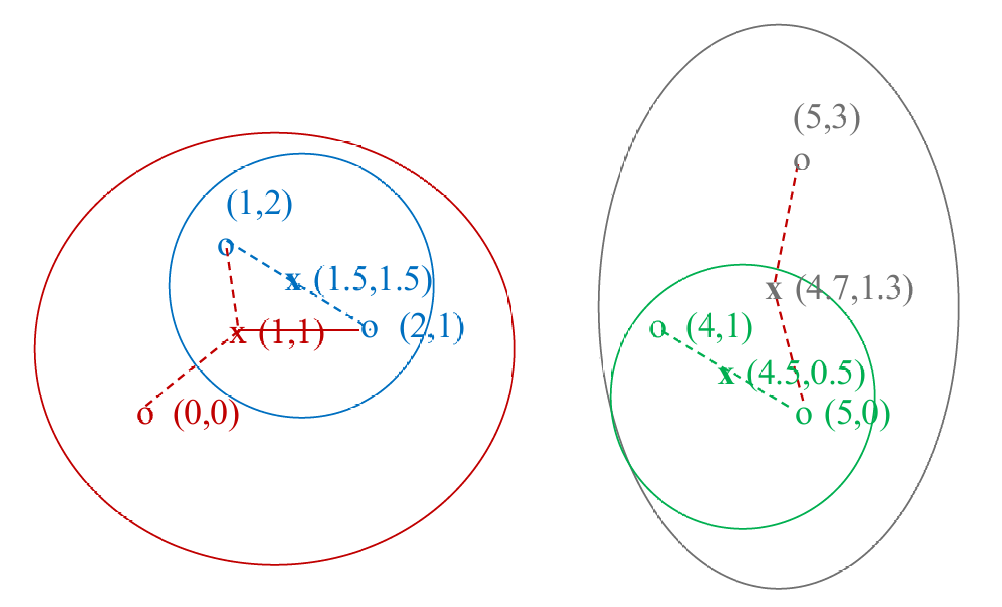
我们初始的六个数据点是：(0,0)，(1,2)，(2,1)，(4,1)，(5,0)，(5,3)
我们第一步计算可以得到(1,2)，(2,1)和(4,1)，(5,0)相距最近，但我们这里以先合并(1,2)，(2,1)为例，我们将其合并为一个聚类，我们得到的这个新聚类的质心计算可以得出是(1.5,1.5)。下一步我们合并(4,1)，(5,0)，同样地得到质心为(4.5,0.5)。
我们现在剩余4个聚类，我们计算它们之间的距离，发现(0,0)和(1.5,1.5)最近，因此这次合并这两个聚类，计算得到新的质心为(1,1)。剩余的三个聚类，同样地，我们发现(4.5,0.5)和(5,3)最近，合并得到新的质心为(4.7,1.3)，最后合并这两个聚类。
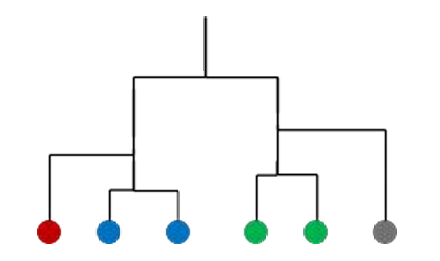
因此我们获得了树状图（Dendrogram）展示了这次聚类的层次结构，如下图所示。

2.1.3 在非欧几里得（Non-Euclidean）

在非欧几里得空间中，传统的距离度量（如欧几里得距离）可能不适用，或者空间的结构更加复杂。
在非欧几里得空间中，我们只能讨论点本身的位置，而不能像在欧几里得空间中那样计算两个点的“平均值”或质心。
在非欧几里得空间中，一个聚类可以由一个“簇心”（clustroid）表示，这个簇心是聚类中其他点“最近”的一个点。
在计算聚类之间的距离时，可以将簇心视为质心，并使用它来计算聚类之间的距离。

这听起来有一些困惑，我们下面的这张图。

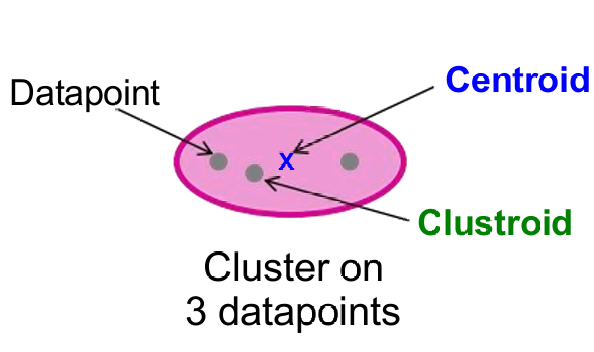
质心（Centroid）：
质心是聚类中所有数据点的平均位置。这意味着质心是一个“人工”点，它通过计算聚类中所有点的坐标平均值得到。
质心用于表示聚类的位置，特别是在聚类算法中，如 k-均值聚类，质心被用作聚类的代表点。
簇心（Clustroid）：
簇心是聚类中现有的数据点，它是“最接近”聚类中所有其他点的点。
与质心不同，簇心是一个实际存在于数据集中的点，而不是计算得到的平均点。
在层次聚类中，簇心用于确定聚类之间的距离，特别是在分裂型（Divisive）层次聚类中，簇心被用作计算聚类间距离的基础。

这里的最接近有三种可能的方案：

1. 最小最大距离（Smallest maximum distance）：
   这个定义关注的是簇心到聚类中其他点的最大距离。如果一个点是聚类中距离最远的点最近的，那么它就是聚类中的“最近”点。
2. 最小平均距离（Smallest average distance）：
   这个定义计算簇心到聚类中所有其他点的平均距离。如果一个点是聚类中所有其他点的平均距离最近的，那么它就是聚类中的“最近”点。
3. 最小平方和距离（Smallest sum of squares of distances）：
   这个定义考虑的是簇心到聚类中所有其他点的距离平方和。这种方法通常用于最小化误差平方和，是许多聚类算法（如 k-均值聚类）中常用的方法。

下面给出第三种方案的数学表达式。
对于聚类$C$中的任意点$x$，簇心$c$是使得以下距离度量最小的点：${\min }_c{\sum }_{x\in C}d(x,c{)}^2$，其中$d(x,c)$是点$x$和$c$之间的距离。

2.1.4 停止条件（Termination Condition）

何时停止合并聚类是一个关键问题，因为它决定了聚类的数量和结构。

方案 1：预先确定聚类数量 k：
在聚类开始之前，预先选择一个聚类数量 k。
当达到 k 个聚类时停止合并聚类。
这种方法适用于当我们对数据的自然分类数量有先验知识时，即数据自然地可以分成 k 个类别。

方案 2：当合并会导致低“凝聚力”时停止：
当下一次合并会导致创建一个“坏”聚类时停止。
这里的“坏”聚类指的是凝聚力（cohesion）低的聚类，即聚类中的点彼此之间不相似，或者聚类与其他聚类之间的距离太近。
这种方法不依赖于预先设定的聚类数量，而是根据聚类的质量来决定何时停止。

下面给出评估凝聚力（cohesion）的三种方案：

• 方案 2.1：使用合并聚类的直径
  定义：合并聚类的直径是聚类中任意两点之间的最大距离。
  应用：通过计算合并后的聚类中的最大距离来评估聚类的凝聚力。如果这个距离过大，可能表明聚类内部的点不够紧密，需要进一步分裂或调整。

• 方案 3.2：使用半径
  定义：半径是聚类中任意一点到聚类质心（或簇心）的最大距离。
  应用：通过计算聚类中点到质心的最大距离来评估聚类的凝聚力。这种方法常用于 k-均值聚类算法中，其中质心是聚类中所有点的平均位置。

• 方案 3.3：基于密度的方法
  定义：密度定义为单位体积内的点数，例如，聚类中的点数除以聚类的直径或半径。
  应用：通过计算聚类中点的密度来评估聚类的凝聚力。密度越高，表示聚类内部的点越紧密。这种方法可以进一步细化，例如使用半径的平方或立方来调整密度的计算，以更好地反映聚类的紧密程度。

2.1.5 具体实现

在朴素的层次聚类实现中，算法在每一步都需要计算所有聚类对之间的成对距离。
然后，算法会合并距离最近的两个聚类。
这种方法的时间复杂度为$O(N^3)$，其中$N$是聚类的数量。这是因为在每一步中，都需要计算$N\times (N-1)/2$次距离（因为每对聚类之间只需要计算一次距离）。

我们可以使用优先队列（priority queue）的优化实现可以减少计算时间，将时间复杂度降低到$O(N^{2}logN)$。
优先队列是一种数据结构，它允许快速地访问队列中最小（或最大）的元素。
在层次聚类中，优先队列可以用来快速找到最近的聚类对进行合并。

尽管优化后的实现将时间复杂度降低到 $O(N^{2}logN)$，但对于非常大的数据集，这种计算仍然可能过于昂贵。
特别是当数据集太大而无法完全装入内存时，这种计算方式可能不适用。

3. k-均值聚类算法（K-means clustering algorithm）

k-均值聚类算法通常假设数据点位于欧几里得空间中，并且使用欧几里得距离（即直线距离）来衡量点之间的距离。

算法开始时，需要预先指定$k$，即要形成的聚类数量。
初始化聚类的过程涉及选择每个聚类的初始中心点（质心）。
一种常见的初始化方法是随机选择一个点作为第一个聚类的中心，然后选择$k-1$个其他点，这些点尽可能远离之前选择的点。
例如，如果$k=3$，那么首先随机选择一个点作为第一个聚类的中心，然后选择另外两个点，这两个点尽可能远离第一个点以及彼此之间也尽可能远。

更新聚类（Populating Clusters）：

• 步骤 1：对于每个数据点，将其分配到最近的质心（centroid）所在的聚类。质心是聚类中所有点的平均位置。
• 步骤 2：在所有点都被分配到相应的聚类后，更新$k$个聚类的质心位置。新的质心是重新分配后的聚类中所有点的平均位置。
• 步骤 3：重新将所有点分配到它们最近的质心。有时，这个过程会导致点在不同的聚类之间移动。

重复执行步骤 2 和 3，直到算法收敛。收敛意味着：
点不再在不同的聚类之间移动，即每个点都稳定地属于同一个聚类。
质心的位置稳定下来，即质心不再显著变化。

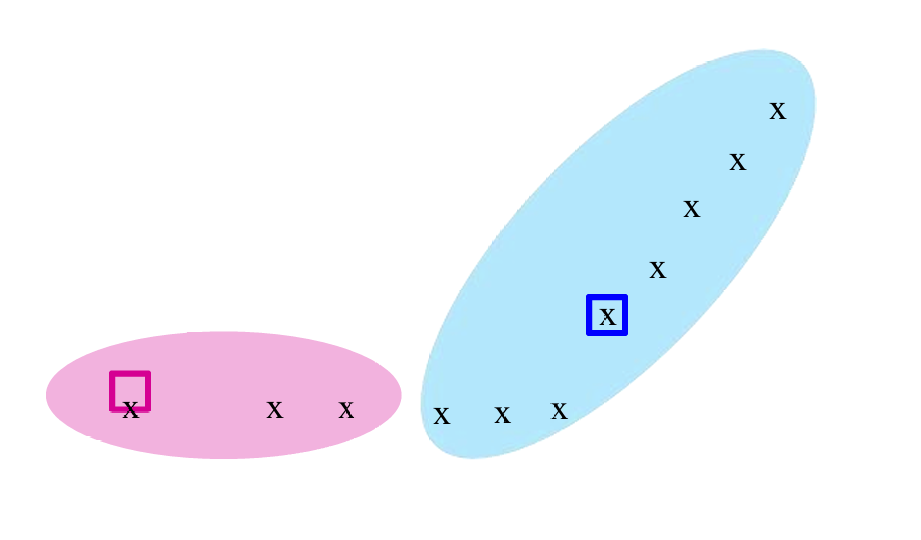
下面给出一个示例（x是数据点，框是质心）。
我们指定$k=2$，所以选择两个点为聚类的中心也就是质心。对于每个数据点，将其分配到最近的质心（centroid）所在的聚类。

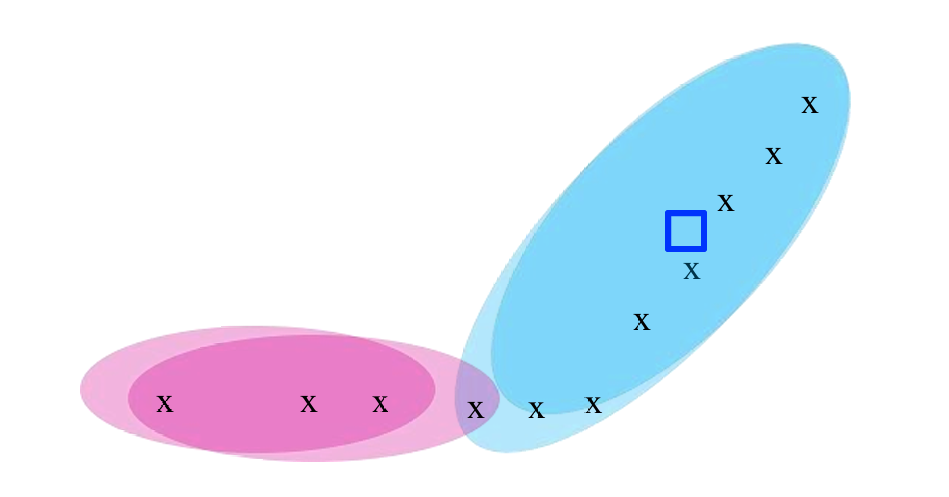
得到这个结果后，我们更新这2个聚类的质心位置，并重新分配所有点分配到它们最近的质心。

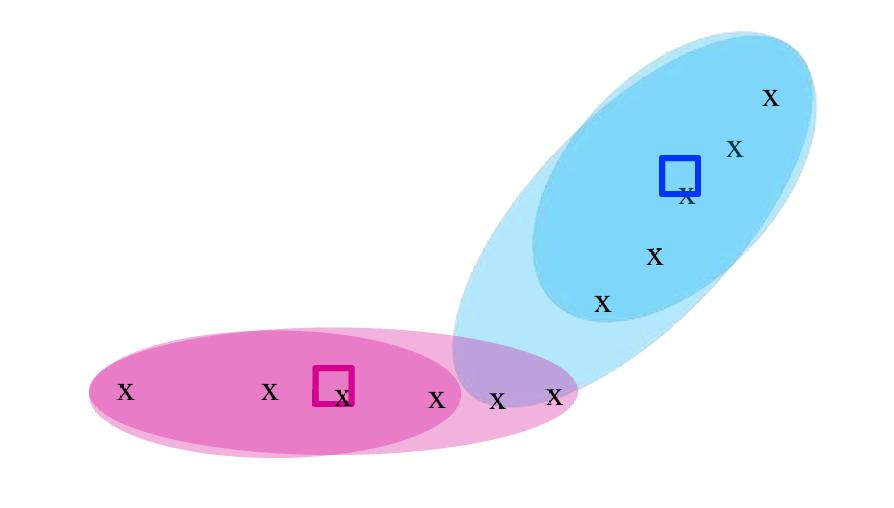
一直重复更新质心位置以及重新分配点到它们最近的质心，直到不再变化。

3.1 如何选择合适的$k$

在 k-均值聚类中，选择正确的聚类数量$k$是一个关键步骤，因为它直接影响聚类结果的质量。
如果$k$太小，这会导致每个聚类包含的数据点较多，质心（centroid）与聚类中某些点的距离较长。

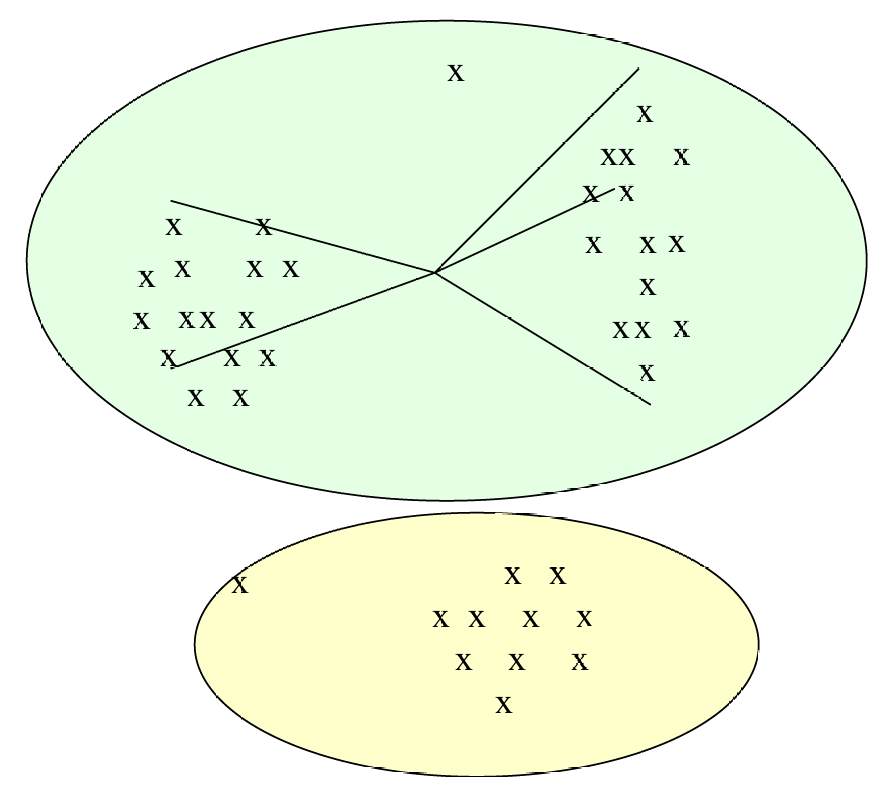
如果$k$太大，聚类数量过多时，平均距离的改善很小。这意味着增加更多的聚类并不能显著减少数据点到质心的平均距离。

合适的$k$值使得聚类内部的数据点到质心的距离相对较短。

为了找到最佳的$k$，可以尝试不同的$k$值，并观察聚类结果的变化。
一种评估不同$k$值的方法是观察聚类结果中点到其聚类质心的平均距离的变化。
通过比较不同$k$值下的平均距离，可以评估聚类的质量。理想情况下，较小的平均距离表示点与其聚类中心更接近，聚类效果可能更好。

一种常用的方法是绘制不同$k$值下的平均距离（或其他聚类内聚度量）的变化图，寻找图中的“肘部”（elbow point），即曲线开始变平缓的点。这个点通常被认为是一个合适的$k$值。

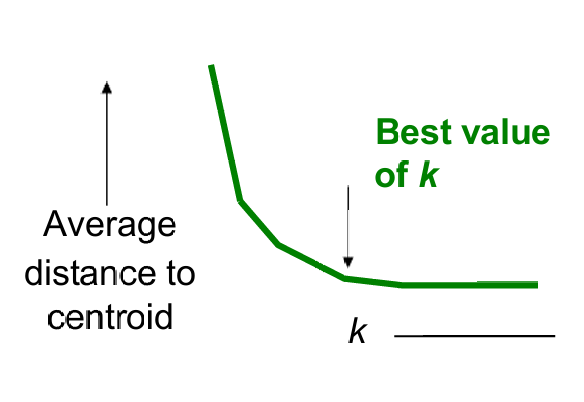
随着$k$值的增加，到质心的平均距离迅速下降。
当$k$值增加到某个点后，平均距离的下降速度变慢，曲线趋于平缓，这表明增加更多的聚类对聚类质量的改善不大。

3.1.1 选择质心的方法

1. 采样（Sampling）
   层次聚类：首先使用层次聚类方法对数据进行聚类，以获得$k$个聚类。
   选择点：从每个聚类中选择一个点作为初始质心。例如，可以选择每个聚类中距离质心最近的点。
   内存适应性：这种方法适用于可以适应主内存的数据集，因为每个聚类中的点数较少。
2. 选择“分散”的点集
   随机选择第一个点：随机选择第一个点作为初始质心。
   选择后续点：选择下一个点时，选择距离已选择的点尽可能远的点，即选择最小距离最大的点。
   重复：重复上述过程，直到选择出$k$个点作为初始质心。

3.2 时间复杂度

在每一轮迭代中，算法需要精确地检查每个输入点一次，以找到最近的质心（centroid）。
每轮的时间复杂度为$O(kN)$，其中$N$是数据点的数量，$k$是聚类的数量。
算法需要多轮迭代才能收敛到最终的聚类结果。
所以这进一步增加了算法的总计算量。

3.2.1 BFR（Block Friendly Randomization）算法

BFR算法是一种用于数据聚类的方法，特别是在处理大规模数据集时。

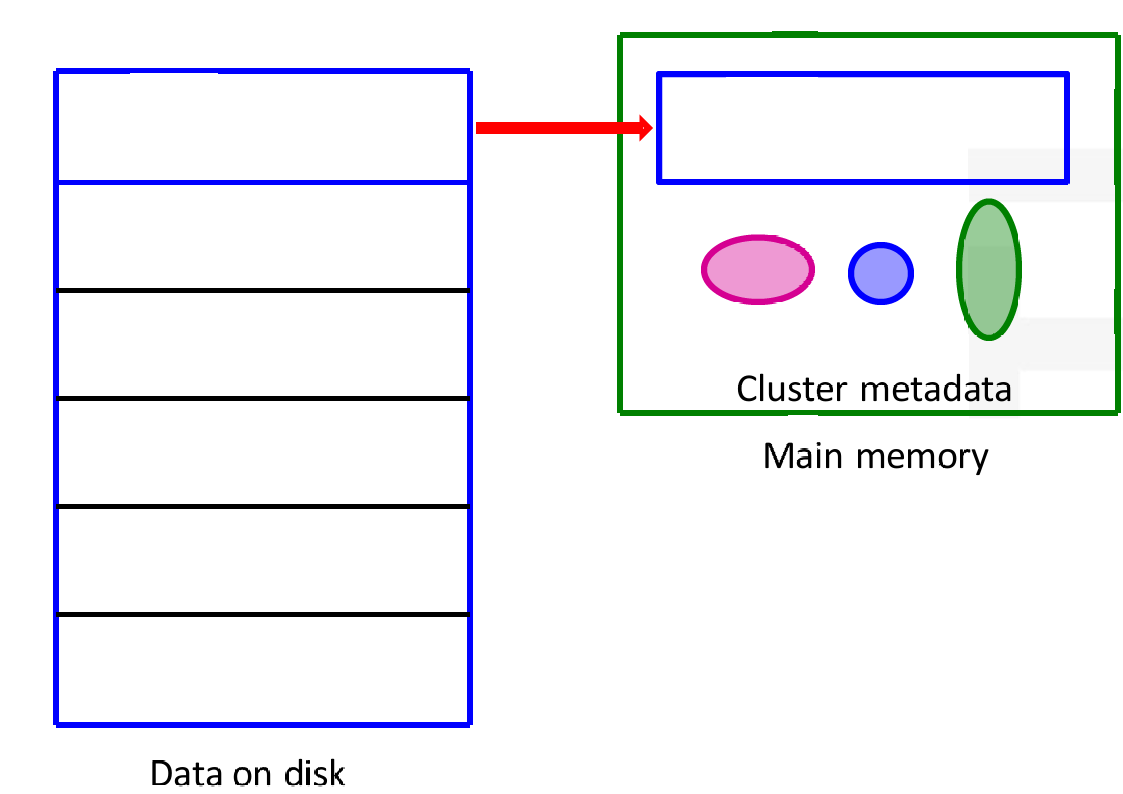
算法从磁盘上读取数据块，并将其加载到主内存中。
这些数据块随后用于聚类分析。
聚类元数据（Cluster metadata）存储在主内存中，用于管理聚类过程中的信息。

BFR算法通过将数据块从磁盘读取到内存，然后在内存中进行聚类分析。
这种方法适用于处理大规模数据集，因为它可以有效地管理内存和磁盘之间的数据传输。
聚类元数据存储在内存中，用于指导聚类过程，确保数据点被正确地分配到相应的聚类中。

总结来说，BFR算法通过优化数据的读取和内存管理，可以显著提高大规模数据集上聚类分析的性能。

3.2.1.1 BFR算法的局限性

BFR算法在聚类分析中做出一些强假设：
聚类在每个维度上都是正态分布的（即高斯分布）。
坐标轴是固定的，这意味着算法假设数据的分布是轴对齐的，不能很好地处理椭圆形或角度倾斜的聚类。

如下图所示。

左边的数据BFR可以轻松解决，但是中间的和右边的数据的分布都不是轴对齐的，BFR算法没法解决。

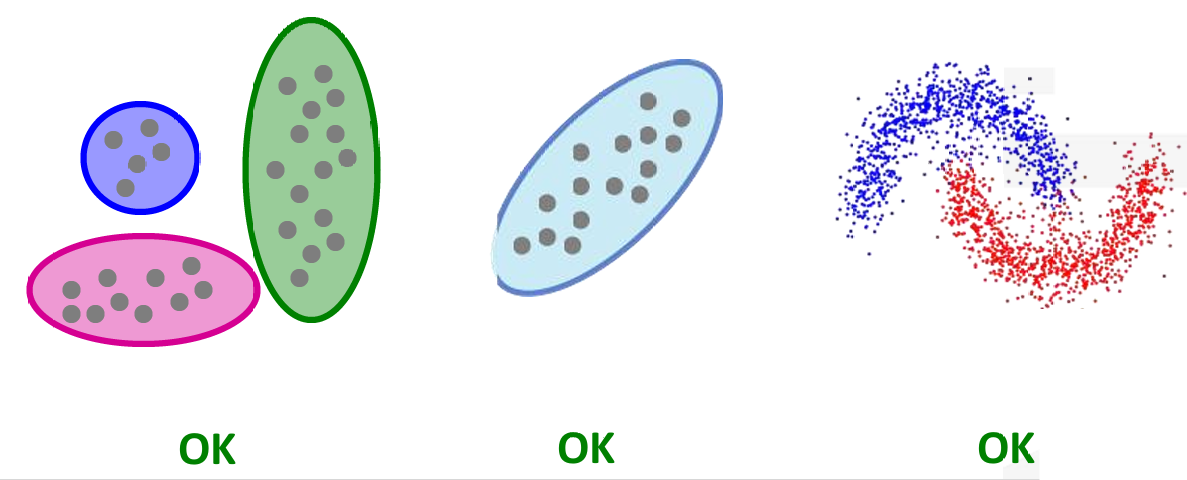
3.2.2 CURE（Clustering Using REpresentatives）算法

CURE（Clustering Using REpresentatives）算法旨在解决传统聚类算法（如 k-均值聚类）在处理复杂形状聚类时的局限性。
这包括：

1. 形状假设过强
   k-均值：隐式要求簇为球形且体积相近，否则平方误差目标会把大簇撕裂、把小簇吞并。
   BFR：更进一步要求各维正态+轴对齐，任意角度的椭圆、环形、月牙形都会被切分成多块。
2. 对“密度变化”不敏感
   同一簇内若密度差异大（高密度核+低密度晕），k-均值会把晕圈单独判成新簇；密度峰值型算法（DBSCAN、Mean-Shift）则无此问题。
3. 对“流形/非凸”结构失效
   月牙、双螺旋、环形等非凸流形，欧氏距离下最近邻未必属于同簇
   k-均值、BFR 会把月牙端点强行拉直成椭圆；单链接虽能保留形状，但会“链式”桥接噪声，把两个月牙串成一条长蛇。
4. 对“桥接噪声”脆弱
   两簇间若存在少量噪声点形成密度桥，k-均值会因全局平方误差最小而把两簇合并；全链接则对单个离群点过度敏感，易把大簇撕裂。
5. 维度灾难放大形状偏差
   高维空间几乎“所有点对距离相近”，球形假设进一步失真；BFR 的轴对齐假设在相关特征维度下会把斜向椭球切成多个“薄饼”。
6. 参数与先验知识难设定
   k-均值需预先指定 k 且对初值敏感；BFR 需额外设定各维方差阈值；层次聚类需选定距离度量及截断高度——这些参数在无标签、形状未知场景下几乎无法合理估计。

CURE 是一种聚类算法，它使用代表性点（representative points）来表示聚类。
CURE算法假设使用欧几里得距离来度量点之间的距离。
CURE算法允许聚类具有任意形状，这使得它能够处理椭圆形、环形或其他非球形聚类。
CURE算法使用一组代表性点来表示每个聚类，而不是使用单一的质心。
因此对于前面的三个例子，CURE算法都可以解决。

4. 总结

聚类分析的目标是给定一组点（数据点），基于点之间的距离概念，将这些点分组到若干个聚类中。

具体聚类算法有：

1. 凝聚型层次聚类（Agglomerative hierarchical clustering）：这是一种自底向上的层次聚类方法，它从每个点作为一个单独聚类开始，逐步合并最近的聚类，直到满足某个终止条件。
2. k-均值聚类（k-means clustering）：这是一种广泛使用的聚类算法，它通过迭代地移动聚类中心来最小化每个点到其聚类中心的距离平方和。
3. BFR（Block Friendly Randomization）：这是一种优化数据读取和处理策略，旨在提高聚类算法在处理大数据集时的效率。
4. CURE（Clustering Using REpresentatives）：这是一种聚类算法，它使用代表性点来表示聚类，允许聚类具有任意形状。