GJOI 11.6 题解

1.CF2007C Dora and C++

题意

思路

根据裴蜀定理，记 $g=\gcd (a,b)$，不管经过多少次操作，所有数 $\mathrm{mod}g$ 的余数不变，且所有数都能表示为 $k_{i}g+x$，其中所有数的 $k_{i}g$ 相同、$x\in [0,g)$。

于是考虑在余数操作。对余数 $p_i$ 排序，初始就是 $p_n-p_1$，即最大值减最小值。更改的话可以尝试让每个 $p_i$ 成为最大值而 $p_{i+1}$ 成为最小值，即把 $p_{1\sim i}$ 全部 $+g$，每次 $ans\leftarrow p_i+g-p_{i+1}$。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=1e5+9;
ll Q,n,a,b,p[N];
int main()
{freopen("game.in","r",stdin);freopen("game.out","w",stdout);scanf("%lld",&Q);while(Q--){scanf("%lld%lld%lld",&n,&a,&b);ll g=__gcd(a,b);for(int i=1;i<=n;i++){scanf("%lld",&p[i]);p[i]%=g;}sort(p+1,p+n+1);//	printf("%lld\n",g);ll ret=p[n]-p[1];for(int i=1;i<n;i++)ret=min(ret,p[i]+g-p[i+1]);printf("%lld\n",ret);}return 0;
}

2.洛谷 P7668 JOI2018 Final 团子制作 / Dango Maker

题意

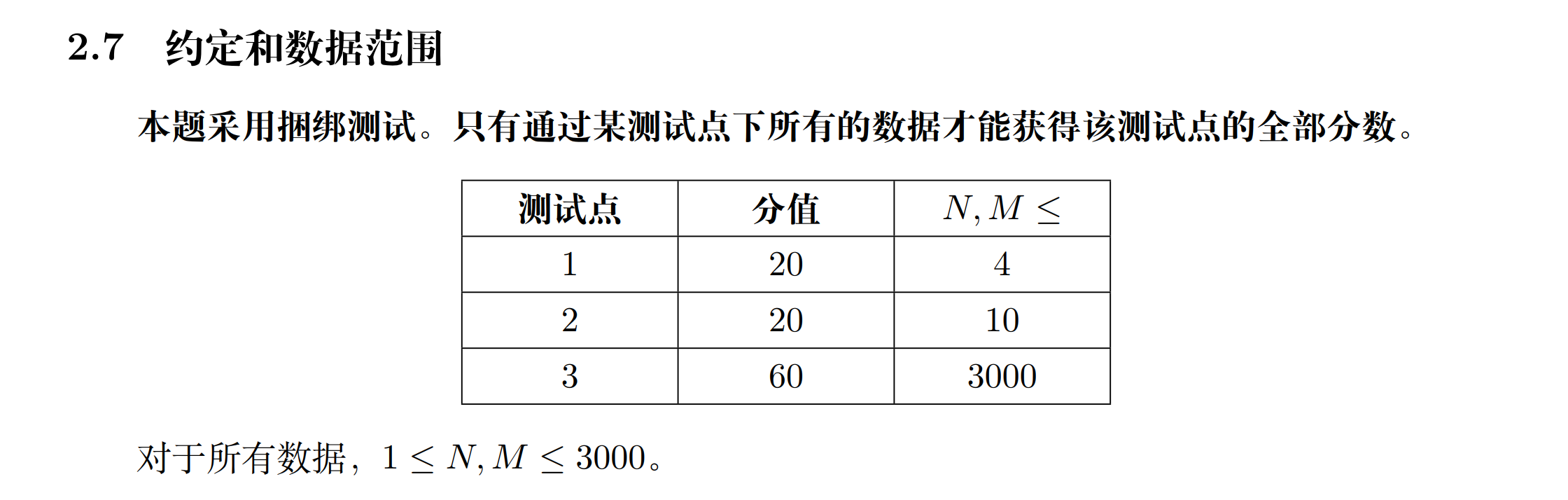
思路

非常神仙的一道题。一开始我往二分图想，发现复杂度爆大然后写了一个假的并查集，后来机房大佬说这是一个特殊的二分图，可以很快地做完。

首先 RGW 可以用 G 和方向 $0/1$ 方便地表示一个串。于是以 G 作为标识点，设 $f_{i,j,op}$ 表示在 $(i,j)$ 能否得到横 / 竖的 RGW。

我们按照 $i:1\to n,j:1\to m$ 的顺序遍历，发现右上角先遍历的的可能会和当前的冲突。这里保证已经处理完的要处于合法状态

考虑转移右上角带来的影响。假若右上角放置了东西（$\exists o{p}^{\prime }=0/1,f_{i+1,j-1,o{p}^{\prime }}=1$）：

• 如果 $o{p}^{\prime }=0/1$ 只有一个 dp 值是 $1$ 的，显然 $(i,j)$ 保留和 $o{p}^{\prime }$ 同向的是优的（否则会破坏掉右上角的合法状态）；
  

• 如果右上角没有东西，或者右上角依然有两个 $o{p}^{\prime }$ 的 dp 值是 $1$（两个情况同理），那就两个都延续下来。直到后面出现某个 G 只有横 / 竖一个 RGW（只有一个 $op$ 的 dp 值为 $1$）；
  

• （延续第二种情况）或者说后面全是 G 横竖都有的（两个 $op$ 的 dp 值为 $1$），因为每个有 RGW 的 G 至多留一个，所以到某个末梢就会全选横 / 竖的，横 / 竖都不劣。

• 对于下图所示的，能卡掉一车人并查集的图，也能解决：
  

每个点最多留一个，即 $f_{i,j,0}|f_{i,j,1}$。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=3004;
int n,m;
char c[N][N];
bool chkx(int x,int y)
{return x>=3&&y>=1&&c[x-2][y]=='R'&&c[x-1][y]=='G'&&c[x][y]=='W';
}
bool chky(int x,int y)
{return y>=3&&x>=1&&c[x][y-2]=='R'&&c[x][y-1]=='G'&&c[x][y]=='W';
}
bool f[N][N][4];
int main()
{freopen("jiaozi.in","r",stdin);freopen("jiaozi.out","w",stdout);scanf("%d%d",&n,&m);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)cin>>c[i][j];int ans=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(c[i][j]=='G'){f[i][j][0]=chky(i,j+1);f[i][j][1]=chkx(i+1,j);if(f[i-1][j+1][0]||f[i-1][j+1][1])//上面有填 {if(!f[i-1][j+1][0])f[i][j][0]=0;if(!f[i-1][j+1][1])f[i][j][1]=0;}ans+=(f[i][j][0]|f[i][j][1]);}}}printf("%d",ans);return 0;
}

反思

没有往“标识点”去想，于是让 dp 变得非常困难。

3.洛谷 P9019 USACO23JAN Tractor Paths P

题意

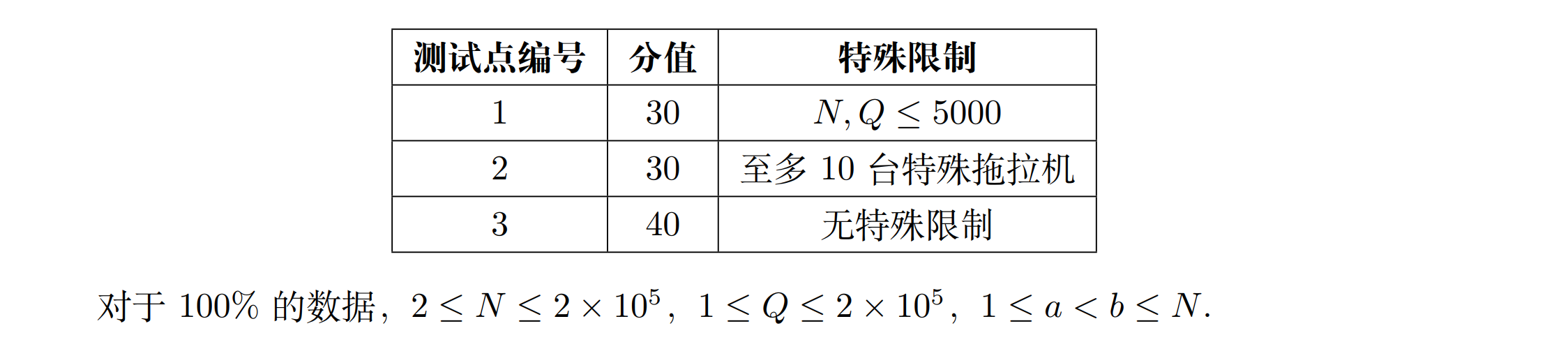
思路

这种在直线上，要在区间和区间之间穿梭，或者要跳一段区间的，倍增往往是常用手段——可以从 $O(n)$ 暴力枚举到 $O(\log n)$。

设 $f_{i,j}$ 表示，从 $i$ 开始，向右换乘 $2^j$ 个拖拉机，能到达最大的拖拉机编号，因为问的是跳到某个拖拉机 $b$ 的次数。对于拖拉机 $i$ 的完整区间 L~R 内，最靠右的 L 所对应的拖拉机编号，就是 $i$ 换乘 $1$ 次能够到达的最大拖拉机编号，即 $f_{i,0}$。

因为拖拉机的左右端点分别顺次布置，所以从 $a\to x$，如果 $b<f_{a,2_j}$ 那么 $b$ 必然能在 $2^j$ 步以内跳到。更新倍增数组，可以求解第一问。

对于第二问，我们维护跳跃过程中会经过多少特殊拖拉机。首先 $a\to b$ 经过的拖拉机编号肯定 $\in (a,b)$，会跳过多段连续编号区间，这些编号区间必然不交（因为是最短路径）。于是相应地维护 $g_{i,j}$ 表示 $i$ 跳 $2^j$ 步跳到的最小拖拉机编号，每次跳跃求编号区间有多少特殊拖拉机，相当于在编号区间上前缀和相减了，这个和也可以用倍增维护。通过第一问答案还原回去即可。

具体细节见代码。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2e5+9,M=20;
ll n,Q;
char s[N<<1];
bool spc[N];
ll ss[N];
struct trk
{ll l,r;//换乘 2^0=1 次，最远可跳区间编号 
}a[N];
ll f1[N][M],f2[N][M],s1[N][M],s2[N][M];
ll jump(ll x,ll y)
{ll ret=0;for(int i=18;i>=0;i--)if(f1[x][i]!=-1&&f1[x][i]<y)ret|=(1<<i),x=f1[x][i];return ret;
}
int main()
{
//	freopen("tractor.in","r",stdin);
//	freopen("tractor.out","w",stdout);scanf("%lld%lld%s",&n,&Q,s+1);ll id=0,cur=0;for(int i=1;i<=2*n;i++){if(s[i]=='L')id++;else a[++cur].r=id;}id=n+1,cur=n+1;for(int i=2*n;i>=1;i--){if(s[i]=='R')id--;else a[--cur].l=id;}for(int i=1;i<=n;i++){char c;cin>>c;spc[i]=(c-'0');ss[i]=ss[i-1]+(c-'0');}for(int j=0;j<=18;j++)for(int i=1;i<=n;i++)f1[i][j]=f2[i][j]=-1;for(int i=1;i<n;i++){f1[i][0]=a[i].r;s1[i][0]=ss[a[i].r];}for(int i=n;i>1;i--){f2[i][0]=a[i].l;s2[i][0]=ss[a[i].l-1];}for(int j=1;j<=18;j++){for(int i=1;i<n;i++){if(f1[i][j-1]!=-1){f1[i][j]=f1[f1[i][j-1]][j-1];if(f1[i][j]!=-1)s1[i][j]=s1[i][j-1]+s1[f1[i][j-1]][j-1];}}}for(int j=1;j<=18;j++){for(int i=n;i>1;i--){if(f2[i][j-1]!=-1){f2[i][j]=f2[f2[i][j-1]][j-1];if(f2[i][j]!=-1)s2[i][j]=s2[i][j-1]+s2[f2[i][j-1]][j-1];}}}while(Q--){ll x,y;scanf("%lld%lld",&x,&y);ll dis=jump(x,y);//拖拉机数量 ll ret=spc[x]+spc[y];for(int i=18;i>=0;i--){if((dis>>i)&1){ret+=s1[x][i]-s2[y][i];x=f1[x][i];y=f2[y][i];}}printf("%lld %lld\n",dis+1,ret);}return 0;
}

反思

没有及时反映这个是倍增（伤心），而且这类倍增问题不算很熟练，赛后也调了很久。

4.洛谷 P11516 CCO2024 Summer Driving