数据结构精讲：从零到一搞懂队列与循环队列的底层实现

目录导航

引言：当你的电脑“死机”时，它其实在排队

第一部分：队列的定义与抽象数据类型 (ADT)

第二部分：顺序存储队列的痛点——“假溢出”

第三部分：循环队列——优雅的解决方案

关键挑战：满 vs 空，如何区分？

计算队列长度：一个神奇的公式

第四部分：代码实现与注释（循环队列）

第五部分：链式队列——动态伸缩的无限队列

1. 链式队列的结构定义

2. 链式队列入队操作 (EnQueue)

3. 链式队列出队操作 (DeQueue)

4. 链式队列的优劣

第六部分：总结与延伸

---

引言：当你的电脑“死机”时，它其实在排队

你有没有遇到过这种情况：电脑卡得像块砖，鼠标点哪儿都没反应，键盘敲击如石沉大海。当你绝望地按下 Ctrl+Alt+Del 时，它却突然“醒”了过来，把之前所有积压的操作——打开文件、保存文档、点击链接——一股脑儿全给你执行了？

别慌，这并不是什么玄学，而是你的操作系统在背后默默运行着一个“队列”（Queue）。就像移动、联通的客服热线，总有人在排队等待接通；也像打印机，总是按你发送任务的先后顺序，一个接一个地打印。这就是计算机世界里最基础、最重要的原则之一：先进先出 (FIFO)。

今天，我们将深入剖析队列这一经典数据结构的底层实现。我们会从最简单的顺序存储开始，揭示一个令人抓狂的问题——“假溢出”，然后带你领略“循环队列”的精妙设计，看它是如何用一个小小的数学技巧，优雅地解决了这个难题。最后，我们还会附上完整的C语言代码，让你亲手实践，彻底搞懂它！

第一部分：队列的定义与抽象数据类型 (ADT)

队列，顾名思义，就是“排队”。它的核心规则是：只允许在一端（队尾）插入，在另一端（队头）删除。想象一下银行柜台前的队伍，新来的人只能排在队伍末尾，而办理业务的是站在最前面的人。

这种“先进先出”(FIFO) 的特性，使得队列成为处理有序任务的理想工具。无论是操作系统中的进程调度、网络数据包的传输，还是我们日常使用的消息队列，都离不开它。

根据教材定义，队列是一种特殊的线性表，其抽象数据类型（ADT）包含以下核心操作：

• InitQueue(*Q): 初始化一个空队列。
• DestroyQueue(*Q): 销毁队列，释放内存。
• ClearQueue(*Q): 清空队列，使其变为空。
• QueueEmpty(Q): 判断队列是否为空，返回布尔值。
• GetHead(Q, *e): 获取队头元素的值，不删除。
• EnQueue(*Q, e): 将新元素 e 插入到队尾。
• DeQueue(*Q, *e): 删除队头元素，并将其值返回给 e。
• QueueLength(Q): 返回队列中当前元素的个数。

如下图所示，队列就像一条单向通道，元素只能从“入队列”口进入，从“出队列”口离开。

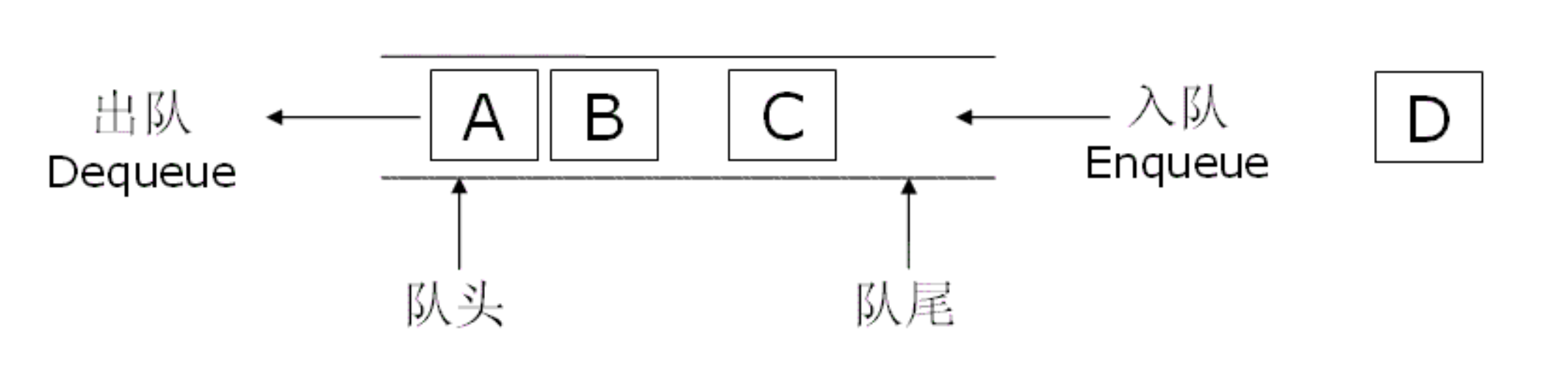
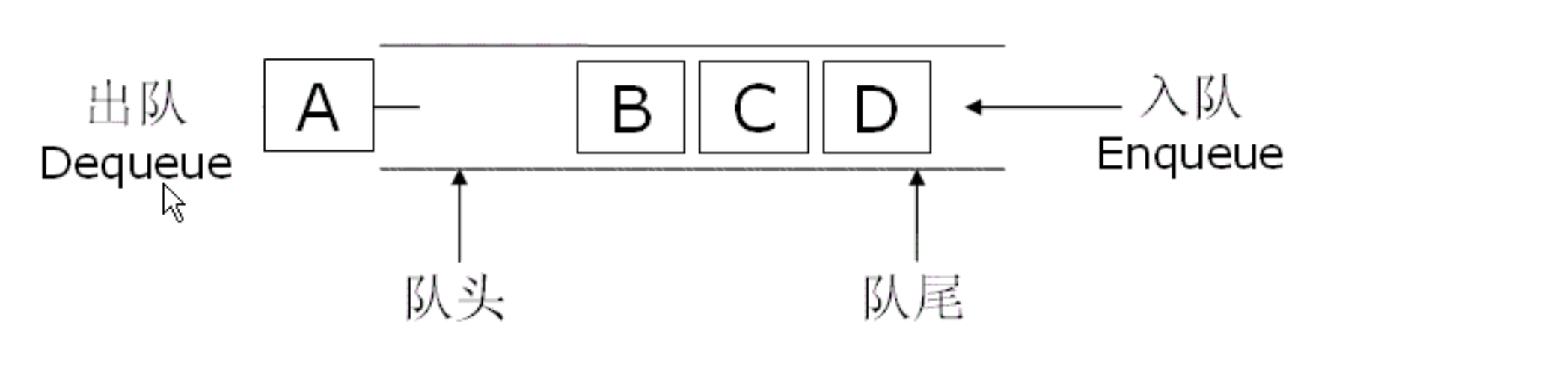
第二部分：顺序存储队列的痛点——“假溢出”

既然队列这么重要，我们该如何在内存中实现它呢？最直观的方法就是使用数组。我们定义两个指针：

• front：指向队头元素的位置。
• rear：指向队尾元素的下一个位置。

初始时，front = rear = 0，表示队列为空。

问题来了！

假设我们有一个长度为5的数组，依次入队 a1, a2, a3, a4。此时，rear 指向索引4的下一个位置，也就是索引5（超出了数组范围！）。接着，我们出队 a1, a2，front 移动到索引2。现在，队列里还有 a3, a4，但如果我们想再入队一个元素 a5，rear 会继续向后移动，最终指向索引5或6，导致数组越界错误。

然而，仔细一看，数组的前两个位置（索引0和1）明明是空的啊！这就是著名的“假溢出”现象——不是真的没空间了，而是因为我们的存储方式太“死板”，让可用空间被“锁”在了数组前端，无法利用。

根本原因：我们强制要求队列元素必须连续存放在数组的前部，导致空间利用率低下。就像一个公交站台，前面的人下车后，后面的人不会往前挪，而是傻傻地等后面有空位才上车，这显然是低效的。

第三部分：循环队列——优雅的解决方案

既然“直线型”存储有问题，那我们何不把它变成“环形”呢？这就是“循环队列”的核心思想：将数组的首尾相连，形成一个逻辑上的环。当 rear 或 front 指针走到数组末尾时，它们会自动“绕回”到数组开头。

关键挑战：满 vs 空，如何区分？

引入循环后，一个新的难题出现了：当 front == rear 时，队列到底是空的还是满的？

• 空队列：没有元素，front 和 rear 都指向同一个位置。
• 满队列：所有位置都被占满，rear 追上了 front。

两者在指针位置上完全一样！这怎么办？

教材为我们提供了两种解决方案：

1. 方法一：设置标志变量 flag

   • 当 front == rear 且 flag = 0 时，队列为空。
   • 当 front == rear 且 flag = 1 时，队列为满。
   • 这种方法需要额外维护一个变量，稍显繁琐。

2. 方法二（推荐）：牺牲一个存储单元

   • 这是最经典、最常用的方法。我们约定，队列永远留一个空位。
   • 队列空：front == rear
   • 队列满：(rear + 1) % QueueSize == front
   • 这里的 % 是取模运算，用于实现“循环”。例如，数组大小为5，当 rear 为4时，(4+1)%5=0，如果此时 front 也为0，则队列已满。

如下图所示，通过牺牲一个单元，我们完美地区分了“空”和“满”两种状态。

计算队列长度：一个神奇的公式

有了循环的概念，计算队列长度就不能简单地用 rear - front 了，因为 rear 可能小于 front。

队列长度 = (rear - front + QueueSize) % QueueSize

这个公式的精妙之处在于：

• 当 rear > front 时（如图1），rear - front 本身就是正数，加 QueueSize 再取模，结果不变。
• 当 rear < front 时（如图3），rear - front 是负数，加上 QueueSize 后变为正数，再取模即可得到正确的长度。

这个公式巧妙地统一了所有情况，堪称“化腐朽为神奇”。

第四部分：代码实现与注释（循环队列）

理论讲完了，是时候动手了！下面是我们用C语言实现的完整循环队列代码，每一行都有详细注释，确保你读完就能理解。

#include <stdio.h>
#include <stdlib.h>#define MAXSIZE 5 // 定义队列的最大容量，这里设为5，实际应用中可调整// 假设队列元素为整型，可根据需求修改
typedef int QElemType;// 假设Status和OK/ERROR已定义
#define OK 1
#define ERROR 0
typedef int Status;// 循环队列的顺序存储结构
typedef struct {QElemType data[MAXSIZE]; // 存放队列元素的数组int front;               // 头指针，指向队头元素int rear;                // 尾指针，指向队尾元素的下一个位置
} SqQueue;/*** 初始化一个空队列*/
Status InitQueue(SqQueue *Q) {Q->front = 0; // 初始化头指针Q->rear = 0;  // 初始化尾指针return OK;
}/*** 计算队列当前长度*/
int QueueLength(SqQueue Q) {// 核心公式：(rear - front + MAXSIZE) % MAXSIZE// 解决了rear < front时的负数问题return (Q.rear - Q.front + MAXSIZE) % MAXSIZE;
}/*** 入队操作* 若队列未满，则插入元素e为新的队尾元素*/
Status EnQueue(SqQueue *Q, QElemType e) {// 判断队列是否已满：(rear + 1) % MAXSIZE == frontif ((Q->rear + 1) % MAXSIZE == Q->front) {return ERROR; // 队列满，插入失败}Q->data[Q->rear] = e;           // 将元素e赋值给队尾Q->rear = (Q->rear + 1) % MAXSIZE; // 尾指针后移一位，利用取模实现循环return OK;
}/*** 出队操作* 若队列不空，则删除队头元素，并用e返回其值*/
Status DeQueue(SqQueue *Q, QElemType *e) {// 判断队列是否为空：front == rearif (Q->front == Q->rear) {return ERROR; // 队列空，删除失败}*e = Q->data[Q->front];         // 将队头元素赋值给eQ->front = (Q->front + 1) % MAXSIZE; // 头指针后移一位，利用取模实现循环return OK;
}// 为了演示，我们添加一个打印队列的函数
void PrintQueue(SqQueue Q) {if (Q.front == Q.rear) {printf("队列为空。\n");return;}printf("队列元素: ");int i = Q.front;while (i != Q.rear) {printf("%d ", Q.data[i]);i = (i + 1) % MAXSIZE;}printf("\n");
}

关键点总结：

• 所有指针移动（front 和 rear）都必须使用 % MAXSIZE 来保证其在数组范围内循环。
• “牺牲一个单元”的策略是解决“满/空”判断的关键。
• 队列长度的计算公式是核心，务必理解其背后的数学原理

第五部分：链式队列——动态伸缩的无限队列

循环队列虽然解决了“假溢出”，但其“容量固定”的缺陷依然存在。如果你要处理一个无法预知大小的任务列表（比如网站的实时请求），你就需要一种能够动态增长、按需分配内存的队列实现方式——这就是链式队列。

链式队列的核心思想是：用单链表来实现队列。链表的头结点作为队头，链表的尾结点作为队尾。入队就是在链表尾部插入新结点，出队就是删除链表头部的结点。

1. 链式队列的结构定义

// 链表结点定义
typedef struct QNode {QElemType data;          // 存放数据元素struct QNode *next;      // 指向下一个结点的指针
} QNode, *QueuePtr;// 链式队列定义
typedef struct {QueuePtr front;          // 队头指针QueuePtr rear;           // 队尾指针
} LinkQueue;

2. 链式队列入队操作 (EnQueue)

Status EnQueue(LinkQueue *Q, QElemType e) {QueuePtr s = (QueuePtr)malloc(sizeof(QNode)); // 申请新结点if (!s) {exit(OVERFLOW); // 内存不足}s->data = e;s->next = NULL;if (Q->rear == NULL) { // 队列为空Q->front = s;Q->rear = s;} else {Q->rear->next = s; // 原队尾指向新结点Q->rear = s;       // 更新队尾}return OK;
}

3. 链式队列出队操作 (DeQueue)

Status DeQueue(LinkQueue *Q, QElemType *e) {if (Q->front == NULL) {return ERROR; // 队列为空}QueuePtr p = Q->front;*e = p->data;Q->front = p->next; // 队头后移// 如果队列变空，需要同时更新rear指针if (Q->front == NULL) {Q->rear = NULL;}free(p); // 释放内存return OK;
}

4. 链式队列的优劣

优势：

• 动态伸缩：内存按需分配，无容量上限。
• 空间利用率100%：无“假溢出”问题。

劣势：

• 额外开销：每个结点需存储指针。
• 内存碎片：频繁申请/释放可能导致性能下降。

第六部分：总结与延伸

通过本文，我们全面掌握了队列的两种核心实现：

特性	顺序队列（循环队列）	链式队列
存储方式	数组	链表
空间效率	高（无指针开销）	较低（有指针开销）
时间效率	O（1）	O（1）
容量	固定大小	动态伸缩
适用场景	元素数量可预估，追求极致性能	元素数量不确定追求灵活

循环队列通过“牺牲一个单元”和“取模运算”的巧妙设计，解决了顺序存储的致命缺陷，是工程中的经典范式。链式队列则凭借其动态伸缩的特性，成为处理不确定规模数据的理想选择。

队列的设计思想（如“用空间换判断清晰”、“用循环利用空间”）不仅适用于数据结构，更是计算机工程中普遍存在的权衡哲学。掌握它们，你就掌握了构建更复杂系统的基础。

当你下次看到“正在排队处理...”的提示时，不妨会心一笑——因为你已经知道，这背后是一个优雅而高效的队列在为你服务。