OFDM理解

在OFDM系统中，对64QAM调制后的信号进行64点IFFT变换，这个“64点”的选择是一个在频谱效率、抗干扰能力和实现复杂度之间取得精妙平衡的结果

它主要基于以下几个核心考量：

1.📡 子载波数量与频谱规划

OFDM的核心思想是将高速数据流拆分成多条低速的子流，让它们在多个正交的子载波上并行传输。在IEEE 802.11a/g/n等标准中，虽然总共有64个子载波位置，但实际用于承载数据的并没有64个。

• ••

  有效数据子载波：通常为 52个。其余的子载波被分配为：

  • ••

    导频子载波：用于信道估计和跟踪相位噪声（例如4个）。

  • ••直流子载波和保护子载波：位于频谱中心（直流）和边缘的子载波被留空，用于防止直流偏移干扰和减少带外频谱泄漏

因此，64点的IFFT完美匹配了这64个频率位置（包括使用的和保留的）。

2.⏱️ 符号持续时间与抗干扰能力

IFFT的点数 N直接决定了每个OFDM符号的持续时间 T_symbol，公式为 T_symbol = N / f_s，其中 f_s是采样频率。

• ••对抗多径效应：无线信号在传播中会因反射产生多个副本，在不同时间到达接收机，造成符号间干扰。OFDM通过插入循环前缀来克服这一问题。循环前缀是每个OFDM符号尾部的复制品，添加到符号开头。64点的符号长度，使得添加循环前缀后，总时长仍在可接受范围内，既能有效对抗常见的多径时延扩展，又不会过分降低数据传输效率

• ••子载波间隔：子载波间隔 Δf = f_s / N。当 N=64且采样率 f_s=20MHz（如802.11a）时，子载波间隔为312.5kHz。这个间隔保证了在通常的无线信道条件下，子载波之间能保持良好的正交性，避免载波间干扰

3.OFDMfpga 实现需要进行截位

在进行IFFT的时候，输入是64位的数据 ，出来是80位 的时域数据

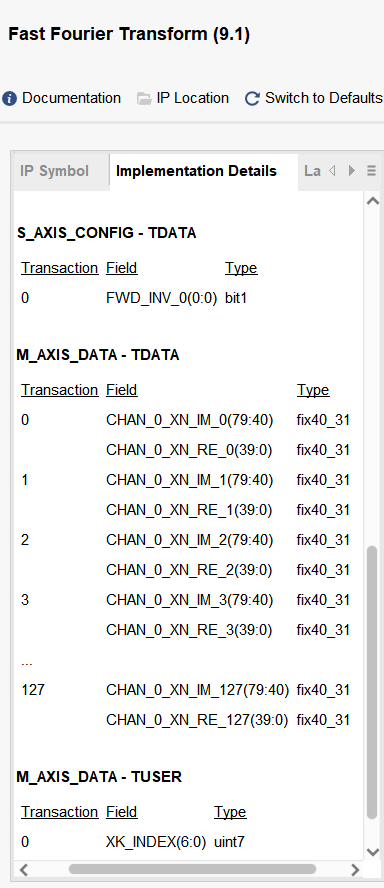
根据DAC等器件知道是12位的器件，然后从IFFT中出来的时域数据需要进行截位 ，根据IP核知道80位的数据 79-40是虚部，39-0是实部，虚部的时候需要截取16位。选取 77-62的16位选取数据。然后根据高位进行选择溢出。

意思就是 [77:62] 这个16位   的最高位77位如果是正数77位为1就说明有溢出，符号位为0，需要钳位77-62，如果77位为0，同时最高位的符号位也为0，说明是正数没有溢出可以截取，对于负数来说，最高位为1 同时如果77位为0说明正数取反+1有进位，溢出了钳位到最小值，否则最高位为1 同时如果77位为1说明正数取反+1没进位可以截取77-62

always @(*) beginif(ifft_output_data[79:77] == 3'b111 || ifft_output_data[79:77] == 3'b000) beginifft_im_out <= ifft_output_data[77:62];endelse if(ifft_output_data[79] == 1'b1) beginifft_im_out <= 16'h8000;//-32768endelse if(ifft_output_data[79] == 1'b0) beginifft_im_out <= 16'h7fff;//32767endelse beginifft_im_out <=16'd0;endendalways @(*) beginif(ifft_output_data[39:37] == 3'b111 || ifft_output_data[39:37] == 3'b000) beginifft_re_out <= ifft_output_data[37:22];endelse if(ifft_output_data[39] == 1'b1) beginifft_re_out <= 16'h8000;//-32768endelse if(ifft_output_data[39] == 1'b0) beginifft_re_out <= 16'h7fff;//32767endelse beginifft_re_out <=16'd0;endendassign ifft_out = {ifft_im_out,ifft_re_out};always @(posedge clk_Modulation) beginif(reset == 1'b1) begintx_add_cyclic_prefix_valid <= 1'b0;endelse if(tx_add_cyclic_prefix_j == 'd159) begintx_add_cyclic_prefix_valid <= 1'b0;endelse if(ifft_out_cnt == 'd95 && ifft_output_valid == 1'b1) begintx_add_cyclic_prefix_valid <= 1'b1;endend

4，为什么实数信号是满足奈奎斯特大于等于2倍，但是复数信号不用

实信号的频谱是“对称的”，有冗余；而复信号的频谱是“单边的”，没有冗余。​ 这个“冗余”直接决定了采样率的要求。

为了让您一目了然，我们先通过一个表格来对比它们的核心区别。

特性	实信号​	复信号​
时域值​	实数（如：1, 0.5, -1）	复数（如：1+0.5j, 0-1j）
频谱结构​	共轭对称（双边谱），关于Y轴对称	非对称（单边谱），可以是任意形状
信息冗余​	有。正负频率部分互为镜像，包含相同信息。	无。正负频率部分可承载不同信息。
奈奎斯特采样率​	Fs ≥ 2B（B为信号正频率带宽）	Fs ≥ B（B为信号总带宽）
物理意义​	真实世界直接存在的信号（如电压、声音）	数学工具，通常由两路实信号（I路和Q路）构成

---

🔍 实信号：为什么需要两倍带宽？

您可以把实信号的频谱想象成一张对称的剪纸。

1. 1.1.对称性（共轭对称）：一个实信号（比如一个音频信号）的频谱，总是关于零频率对称的。这意味着如果你在频率 +f​ 处有一个信号成分，那么在 -f​ 处必定存在一个它的“镜像”。这个镜像是冗余的，并不携带任何新的信息
2. 2.2.

   奈奎斯特准则的适用对象：奈奎斯特采样定理说的是，采样频率必须大于信号整个频谱宽度的两倍，才能保证不丢失信息。对于实信号，它的频谱宽度是从 -B​ 到 +B，总宽度是 2B。因此，采样率必须满足 Fs > 2B * 2？​ 不，这里需要仔细理解：定理中的“两倍”指的是对信号包含的最高频率成分而言的。实信号包含的最高频率成分是+B，所以采样率需要 Fs > 2 * (B)。同时，由于频谱本身的总宽度是2B，这一定律也确保了正负频率部分在采样后不会相互混叠。

所以，对于带宽为B的实信号，需要Fs ≥ 2B的采样率，既是为了捕获最高频率B的成分，也是为了避免其对称的负频率部分在采样后产生混叠。

---

💡 复信号：为什么只需要一倍带宽？

复信号通过数学构造的方式，去除了频谱的对称性，从而“消灭”了冗余。

1. 1.1.解析信号：一种非常重要的复信号叫做解析信号。它可以通过一种叫做希尔伯特变换的数学工具，将一个实信号转换而成。解析信号的关键特性就是：它的负频率部分为零，整个频谱只存在于正频率部分这样，频谱的冗余就被消除了。
2. 2.2.

   I/Q信号：在实际系统中（如软件无线电、通信收发机），复信号表现为I路（In-phase，同相）和Q路（Quadrature，正交）​ 两路实信号。您可以理解为：

   • ••

     复信号 Z(t) = I(t) + jQ(t)

   • ••

     其中，I(t)和Q(t)是两路实信号，它们通常由同一源信号经过相位相差90度的本振调制后得到。

3. 采样率减半：由于复信号的频谱是单边的，它的全部信息都集中在从0到B的频率范围内。因此，它的整个频谱宽度就是B。根据奈奎斯特准则，采样率只需要大于这个宽度即可，即 Fs ≥ B这正是正交采样（I/Q采样）的基础：用两路ADC分别以较低的速率对I和Q两路信号进行采样，等效于以速率Fs对复信号Z(t)进行采样。

5.关于采样的问题

802.11a中规定得是20mh的带宽，需要64点的采样点。但是到时候给adc的时候需要把iq的数据每个需要20mhz，这样的话采样的频率就是40mhz 为了保持频率间隔，要把采样点也提高128。