自己动手写深度学习框架(数值法计算梯度)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing @163.com】
神经网络就是把很多的激励函数放在一起,它们之间通过简单的计算拼接在一起。而训练,就是通过数据、残差方程、梯度下降的办法,优化每一个激励函数里面的参数。所以,在所有参数更新之前,必须获得所有参数的梯度数值,然后用梯度下降的办法优化这些参数值。因此,计算梯度数值是非常重要的一个工作。
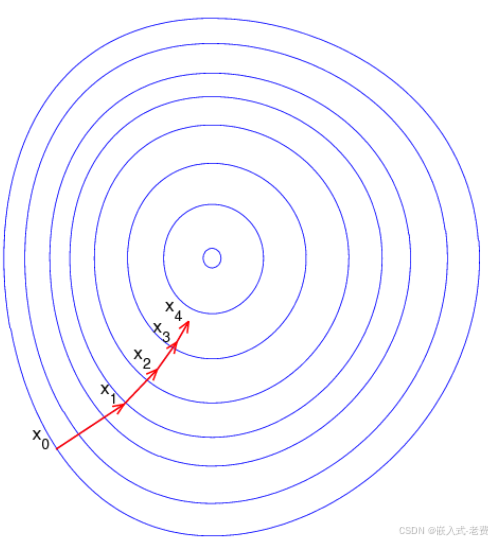
1、梯度数值的计算
计算梯度数值,有两个办法,一个是解析法,也就是直接通过解析方程去求解、证明。这种证明一般都不会太简单,有的时候还需要花费一点时间。还有一种办法,就是数值法。所谓的数值法,就是通过+delta_x,获得一个数值,接着-delta_x,再获得一个数值,通过这样的一种办法,最终(y1-y2)/(2*delta_x) 的办法,获得对应的梯度向量。
2、数值法的优点
优点就是简单、方便、好理解。不管是什么样的激励函数,线性的、非线性的;卷积的、非卷积的;简单的、复杂的,都可以通过这种办法计算对应参数的梯度。
3、数值法的缺点
缺点就是计算量大。如果数据量不大,或者需要训练的数据不多,这种方法还可以尝试下,但是一旦训练的数据比较多,向量空间很大的话,这样的计算远不是一台电脑,或者是几台电脑受得了的。所以,数值法主要用于确认、分析,以及教学的场景。
4、一元参数的梯度计算
我们以y=x**2,来说明如果利用数值法计算梯度值。这里面为了公平,首先我们添加了e-4,接着减去e-4,借助于这种办法计算梯度。
# about single valuedef get_value(x):return x**2def get_radient_by_delta_x(x):x1 = x + 1e-4y1 = get_value(x1)x2 = x - 1e-4y2 = get_value(x2)return (y1-y2)/(2*1e-4)print(get_radient_by_delta_x(3.0))5、二元参数的梯度计算
上面是只有一个参数的情形,如果是多个参数怎么处理呢。其实也是一样的,基本上把另外一个参数当成常量就可以了。
# about multiple valuedef get_value1(x1, x2):return x1*x2def get_radient_by_delta_x1(x1, x2):x11 = x1 + 1e-4y11 = get_value1(x11, x2)x12 = x1 - 1e-4y12 = get_value1(x12, x2)return (y11-y12)/(2*1e-4)def get_radient_by_delta_x2(x1, x2):x21 = x2 + 1e-4y21 = get_value1(x1, x21)x22 = x2 - 1e-4y22 = get_value1(x1, x22)return (y21-y22)/(2*1e-4)print(get_radient_by_delta_x1(3.0, 4.0))
print(get_radient_by_delta_x2(3.0, 4.0))6、多元和复杂结构函数的梯度如何计算
原理其实和一元、二元参数是一样的。计算的过程当中,我们只是对一个变量进行增减,其他参数则保持不变,这样就可以获得一个变化的结果。最终变化的结果,除以这个变量,就可以得到我们所需要的梯度数值。
7、数值法的意义
通过数值法计算梯度,最大的意义其实在于,借助于它,我们可以快速构建一个简单的神经网络。并且通过这个神经网络,还可以进行一定的数据训练。麻雀虽小五脏俱全,这完全可以让我们破除ai训练的迷思,进一步学好神经网络,用好神经网络。
