区间|单调栈
lc522
return 不是其他字符串子序列的字符串.max_len
子序列越长,越不可能是其它字符串的子序列
所以可以 长度从大到小sort 贪心检查

class Solution {
// 判断 s 是否为 t 的子序列
bool isSubseq(string& s, string& t) {
int i = 0;
for (char c : t) {
if (s[i] == c && ++i == s.length()) { // 所有字符匹配完毕
return true; // s 是 t 的子序列
}
}
return false;
}
public:
int findLUSlength(vector<string>& strs) {
ranges::sort(strs, {}, [](const auto& s) { return -s.length(); });
for (int i = 0; i < strs.size(); i++) {
for (int j = 0; j < strs.size(); j++) {
if (j != i && isSubseq(strs[i], strs[j])) {
goto next; // 枚举下一个 i
}
}
return strs[i].length();
next:;
}
return -1;
}
};
判断子序列
class Solution {
public:
bool isSubsequence(string s, string t) {
int i=0,j=0;
while(i<s.size() && j<t.size())
{
if(s[i]==t[j])
i++;
j++;
}
return i==s.size();
}
};
lc2444
遍历数组时记录最近的minK位置、maxK位置
以及超出范围的位置,通过计算有效区间长度来统计同时包含minK和maxK且元素在范围[minK, maxK]内的定界子数组数量
class Solution {
public:
long long countSubarrays(vector<int>& nums, int minK, int maxK) {
long long ans = 0;
int min_i = -1, max_i = -1, i0 = -1;
for (int i = 0; i < nums.size(); i++) {
int x = nums[i];
if (x == minK) {
min_i = i; // 最近的 minK 位置
}
if (x == maxK) {
max_i = i; // 最近的 maxK 位置
}
if (x < minK || x > maxK) {
i0 = i; // 子数组不能包含 nums[i0]
}
ans += max(min(min_i, max_i) - i0, 0);
}
return ans;
}
};
lc795
技巧写法:双指针
遍历数组时记录大于right的位置和大于等于left的位置
计算两者差值来统计最大元素在[left, right]内的子数组数量
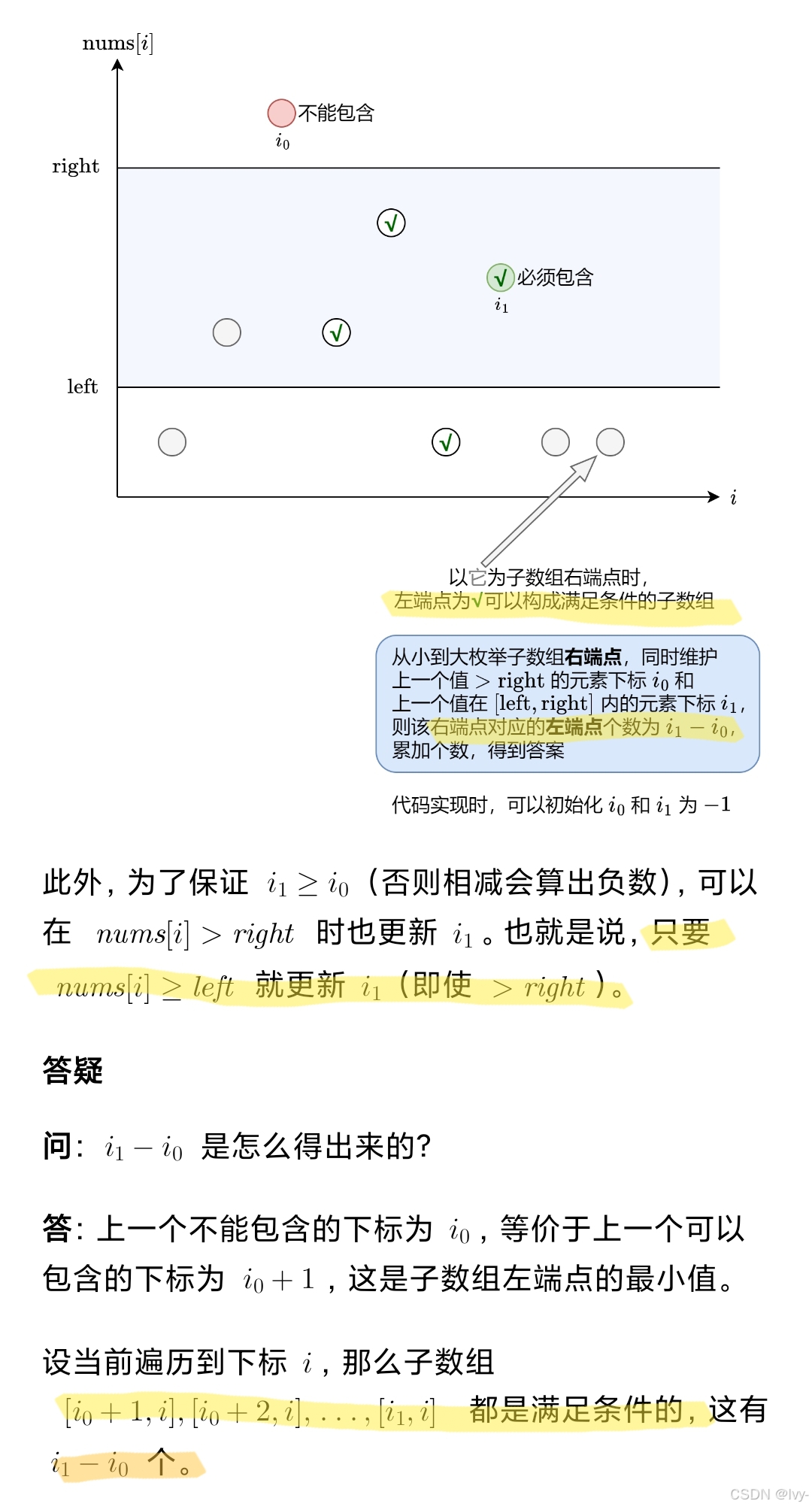
class Solution {
public:
int numSubarrayBoundedMax(vector<int> &nums, int left, int right) {
int n = nums.size(), ans = 0, i0 = -1, i1 = -1;
for (int i = 0; i < n; ++i) {
if (nums[i] > right) i0 = i;
if (nums[i] >= left) i1 = i;
ans += i1 - i0;
}
return ans;
}
};
恰好型滑窗
class Solution {
public:
int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {
auto count = [&](int maxVal) {
int res = 0;
int current = 0;
for (int num : nums) {
current = (num <= maxVal) ? current + 1 : 0;
res += current;
}
return res;
};
return count(right) - count(left - 1);
}
};
贡献度+单调栈
class Solution {
public:
int numSubarrayBoundedMax(vector<int>& nums, int l, int r) {
int n = nums.size();
vector<int> lmin(n), rmin(n);
stack<int> st;
for (int i = 0; i < n; i++) {
while (st.size() && nums[st.top()] <= nums[i]) st.pop();
if (st.empty()) lmin[i] = -1;
else lmin[i] = st.top();
st.push(i);
}
while (st.size()) st.pop();
for (int i = n - 1; i > -1; i--) {
while (st.size() && nums[st.top()] < nums[i]) st.pop();
if (st.empty()) rmin[i] = n;
else rmin[i] = st.top();
st.push(i);
}
int ans = 0;
for (int i = 0; i < n; i++) {
if (nums[i] >= l && nums[i] <= r) {
ans += (i - lmin[i]) * (rmin[i] - i);
}
}
return ans;
}
};
