第五章 神经网络
一、神经网络
神经网络是模拟人脑神经系统的计算模型,由大量简单的处理单元(神经元)相互连接而成。它能通过学习数据自动调整参数,完成分类、预测等任务。
二、神经元模型:神经网络的基础
神经元是神经网络的基本单元,就像大脑中的神经细胞。每个神经元接收输入信号,处理后产生输出。
1. 工作原理
神经元接收来自其他神经元的输入信号,每个输入有权重(表示重要性),总输入减去阈值后,通过激活函数决定输出。激活函数就像“开关”,控制神经元是否“兴奋”。
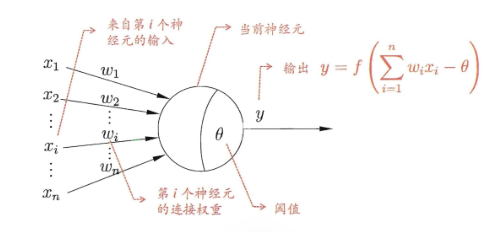
2. 数学表示
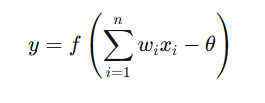

3. 激活函数
阶跃函数:理想中的激活函数,输出 0 或 1(不连续)
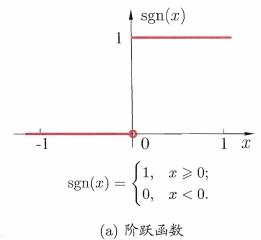
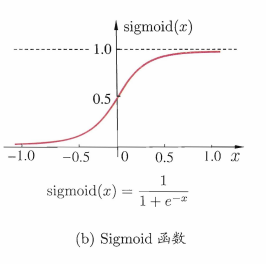
Sigmoid函数:实际常用,将输入压缩到 (0,1) 之间,连续可导
三、感知机(Perceptron)
1. 结构
最简单的神经网络:只有输入层和输出层
输出层使用阶跃函数作为激活函数
2. 学习规则(重点公式)
对于每个训练样本 (x,y),如果预测错误(y^≠y),则更新权重:
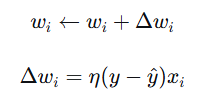
η:学习率,控制更新步长
y−y^:误差信号
3. 局限性
感知机只能解决线性可分问题(如与、或、非)
无法处理异或(XOR)等非线性问题
四、多层前馈神经网络
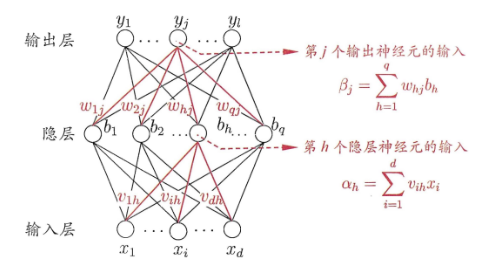
1. 结构
包含输入层、隐藏层、输出层
每层神经元与下一层全连接
层与层之间不存在跨层或反馈连接
2. 表达能力
只要隐藏层神经元足够多,可以逼近任意复杂度的连续函数
五、误差逆传播算法(BP算法)
BP算法是训练多层网络的关键,通过反向传播误差来调整权重和阈值,使网络输出接近真实值。
1. 工作流程

前向传播:输入信号通过网络计算输出。
计算误差:比较输出与真实值。
反向传播:从输出层到隐层,根据误差调整参数。
2. 关键公式
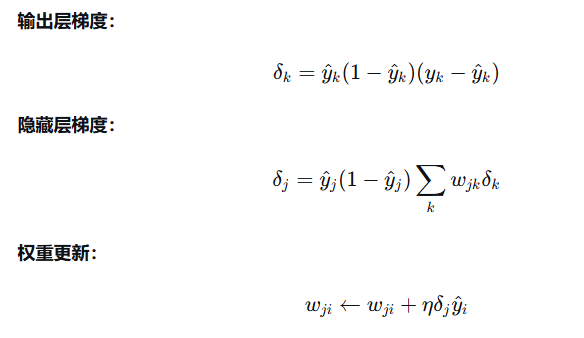
δ:误差信号,表示该神经元对总误差的“责任”
从输出层开始,逐层向前传递误差,并更新权重
使用梯度下降法最小化误差
3.通俗解释
BP算法就像“纠错学习”——网络先猜答案,然后根据错误反向调整每个连接的“强度”,逐步改进。
五、全局最小与局部极小:训练中的挑战
神经网络训练时,目标是最小化误差,但可能陷入局部最优(像在山谷中找不到最低点),而非全局最优。
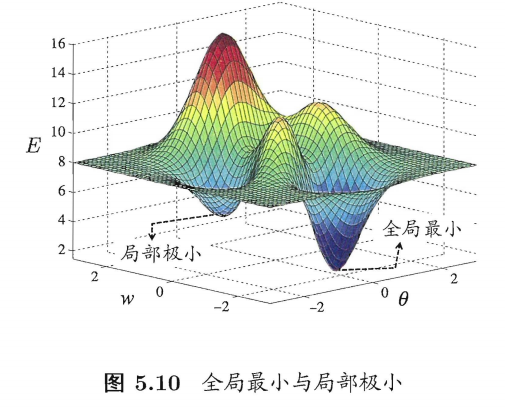
问题描述:误差函数可能有多个“低点”,局部极小是局部最低点,全局最小是整体最低点。图5.10直观展示了这一点。
解决策略:多种方法,如用不同初始参数多次训练、模拟退火(以概率接受更差解跳出局部极小)、随机梯度下降(加入随机性)等。
六、其他常见神经网络:扩展应用
RBF网络:使用径向基函数作为激活函数,适合函数逼近。训练分两步:确定中心,然后用BP调整参数。
ART网络:自适应谐振理论,能增量学习,避免忘记旧知识。它通过竞争机制动态添加神经元。
SOM网络:自组织映射,用于降维和可视化,保持数据拓扑结构。如图5.11所示,神经元在二维网格上竞争。
级联相关网络:结构自适应,训练时动态添加隐层神经元。图5.12展示了训练过程。
Elman网络:递归神经网络,允许反馈连接,能处理时间序列数据。
Boltzmann机:基于能量的模型,包括受限Boltzmann机(RBM),用于深度学习预训练。
七、深度学习:神经网络的进化
深度学习是神经网络的延伸,通过增加隐层数提升模型能力。
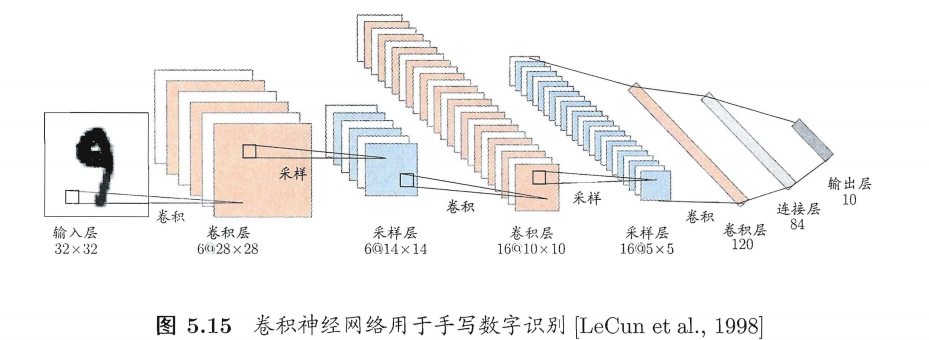
核心思想:使用多隐层网络进行特征学习,自动从数据中提取高层特征。例如,深度信念网络(DBN)用RBM堆叠预训练,卷积神经网络(CNN)用权共享减少参数,如图5.15用于手写数字识别。
优势:深度学习能处理复杂任务,如图像识别,避免手动设计特征。