多粒子模型--交通堵塞
目录
一、核心原理:NaSch 元胞自动机模型
二、代码结构与解析
1. 参数设置
2. 初始化
3. 模拟主循环(核心逻辑)
(1)计算前车距离(避免碰撞的前提)
(2)加速规则
(3)避撞规则
(4)随机减速规则
(5)车辆移动
4. 动画展示
5. 交通流参数分析
三、关键结论与可扩展方向
交通流模拟
这份代码基于元胞自动机(NaSch 模型) 模拟了交通流中堵车现象的形成与演化过程,是交通流理论中经典的模拟方法。下面从整体框架到细节逻辑进行详细解析:
一、核心原理:NaSch 元胞自动机模型
元胞自动机是一种时间、空间、状态都离散的数学模型,由大量简单单元(元胞)组成,通过局部规则演化出复杂全局行为。在交通模拟中:
- 元胞:道路被划分为若干等长 “格子”(元胞),每个元胞要么有车,要么无车。
- 规则:车辆的行驶遵循 4 个核心规则(加速、避撞、随机减速、移动),通过这些局部规则的迭代,模拟出堵车等宏观现象。
二、代码结构与解析
1. 参数设置
L = 100; % 道路长度(元胞数,即格子数量)T = 300; % 模拟时间步数(总演化时长)v_max = 5; % 车辆最大速度(最多移动5个元胞/时间步)p_slow = 0.3; % 随机减速概率(30%概率无原因减速)rho = 0.2; % 初始车辆密度(20%的元胞有车)这些参数控制模拟的基本条件,可通过调整观察不同场景(如高密度更容易堵车)。
2. 初始化
% 随机生成初始车辆位置:1表示有车,0表示无车road = rand(L, 1) < rho; % 生成L个0-1随机数,小于rho的位置设为1(有车)% 初始化车辆速度:有车的位置随机赋予0~v_max的速度velocity = zeros(L, 1);for i = 1:Lif road(i) % 仅对有车的位置赋值速度velocity(i) = randi(v_max); % 随机速度endend% 存储每一步的道路状态(用于后续动画和分析)history = zeros(L, T);history(:, 1) = road; % 第1时间步的初始状态- road:记录当前道路上车辆的位置(0/1 向量)。
- velocity:记录每个位置车辆的速度(0 表示静止)。
- history:存储所有时间步的车辆位置,用于后续动画回放。
3. 模拟主循环(核心逻辑)
循环T-1次(从时间步 2 到 T),每次迭代更新车辆的位置和速度,模拟交通流的演化。每一步包含 5 个关键过程:
(1)计算前车距离(避免碰撞的前提)
distance = zeros(L, 1); % 存储每个车辆前方的空元胞数for i = 1:Lif road(i) % 仅对有车的位置计算d = 0; % 初始距离为0j = i + 1; % 从当前位置的下一个元胞开始while trueif j > L, j = 1; end % 周期性边界(道路首尾相连,模拟环形路)if road(j) % 遇到前车,停止计数break;endd = d + 1; % 空元胞数+1j = j + 1;if d >= v_max % 距离超过最大速度,无需继续计算(反正开不到)break;endenddistance(i) = d; % 记录当前车辆到前车的距离endend- 作用:计算每辆车前方的空位数(与前车的距离),为后续 “避撞” 规则提供依据。
- 周期性边界:道路首尾相连(如j>L时回到 1),避免边界效应影响模拟。
(2)加速规则
for i = 1:Lif road(i) % 仅对有车的位置velocity(i) = min(velocity(i) + 1, v_max); % 速度+1,但不超过最大速度endend- 逻辑:车辆倾向于加速到最大速度(自由行驶状态)。
(3)避撞规则
for i = 1:Lif road(i)velocity(i) = min(velocity(i), distance(i)); % 速度不超过前车距离(防止追尾)endend- 逻辑:如果前方距离小于当前速度,车辆必须减速到与距离相等(确保不撞上前车)。
(4)随机减速规则
for i = 1:Lif road(i) && velocity(i) > 0 % 有车且当前速度>0if rand < p_slow % 以p_slow概率随机减速velocity(i) = velocity(i) - 1;endendend- 逻辑:模拟实际交通中 “无原因减速”(如司机反应、突发情况),是引发拥堵的关键因素之一。
(5)车辆移动
new_road = zeros(L, 1); % 存储新位置的车辆分布new_velocity = zeros(L, 1); % 存储新位置的车辆速度for i = 1:Lif road(i) % 对当前有车的位置% 计算新位置(考虑周期性边界)new_pos = i + velocity(i);while new_pos > Lnew_pos = new_pos - L; % 超出道路长度时,从起点重新计算endnew_road(new_pos) = 1; % 在新位置标记有车new_velocity(new_pos) = velocity(i); % 速度随车辆移动endend% 更新当前状态road = new_road;velocity = new_velocity;history(:, t) = road; % 记录当前时间步的状态- 作用:根据计算出的速度,更新车辆的位置和速度,并存储到history中。
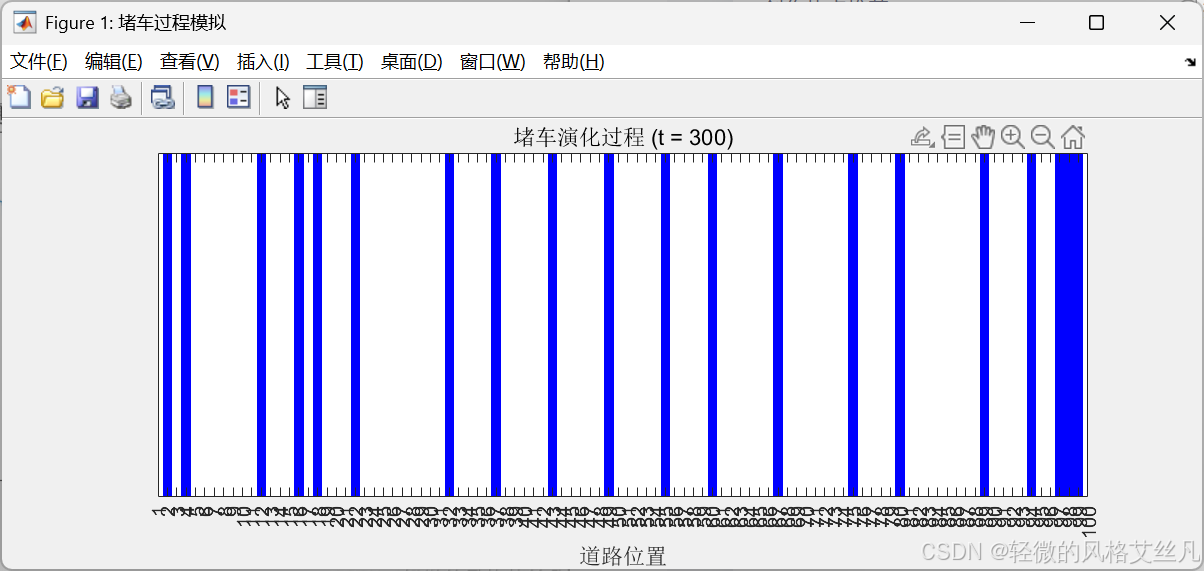
4. 动画展示
figure('Name', '堵车过程模拟', 'Position', [100, 100, 800, 300]);for t = 1:Tclf; % 清除上一帧,只显示当前时间步% 绘制当前时间步的道路状态(转置为行向量,水平显示)imagesc(history(:, t)', [0, 1]); % 用颜色强度表示0(无车)和1(有车)colormap([1 1 1; 0 0 1]); % 白色=无车,蓝色=有车axis xy; % 坐标原点在左上角(符合视觉习惯)xlim([1, L]); % X轴范围:道路位置1~Lylim([0.5, 1.5]); % Y轴范围:只显示一行(道路)set(gca, 'YTick', [], 'XTick', 1:L); % 隐藏Y轴刻度,显示X轴位置xlabel('道路位置');title(['堵车演化过程 (t = ', num2str(t), ')']);drawnow; % 立即刷新图像pause(0.05); % 控制动画速度(数值越小越快)end- 效果:动态展示每一时间步的车辆分布,直观观察车辆如何移动、聚集并形成拥堵。
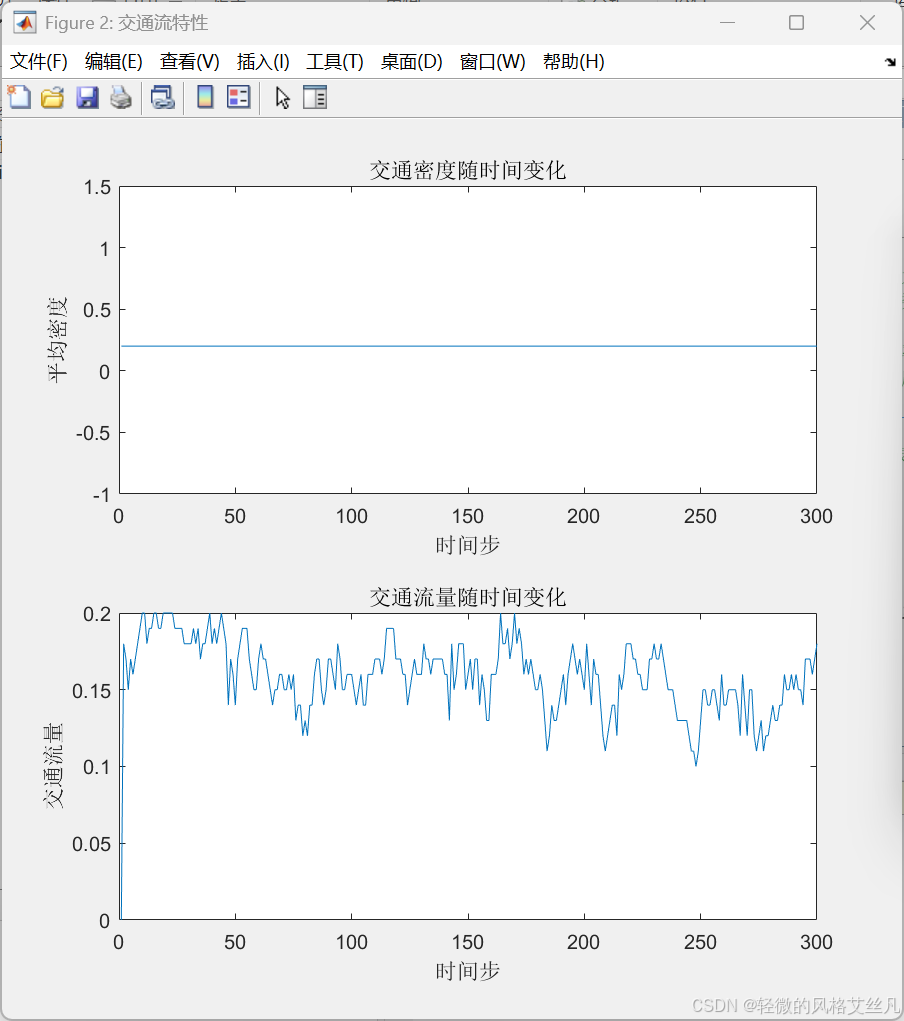
5. 交通流参数分析
% 计算交通流量(单位时间通过的车辆数/道路长度)flow = zeros(1, T);for t = 2:T% 统计从t-1到t移动的车辆数(t时刻有车且t-1时刻无车的位置)moved = sum(history(:, t) & ~history(:, t-1));flow(t) = moved / L; % 单位长度流量end% 绘制密度和流量随时间的变化figure('Name', '交通流特性');subplot(2,1,1);plot(1:T, mean(history, 1)); % 平均密度(有车元胞数/总长度)xlabel('时间步');ylabel('平均密度');title('交通密度随时间变化');subplot(2,1,2);plot(1:T, flow); % 流量随时间变化xlabel('时间步');ylabel('交通流量');title('交通流量随时间变化');- 交通密度:道路上车辆的密集程度(平均有车元胞比例)。
- 交通流量:单位时间通过某点的车辆数(反映道路通行效率)。
- 规律:拥堵时密度升高、流量下降,符合实际交通流特性。
三、关键结论与可扩展方向
- 拥堵形成原因:初始密度过高或随机减速(p_slow)会导致车辆聚集,形成 “堵车波”。
- 参数影响:
- 增大rho(初始密度):更快形成拥堵。
- 增大p_slow(随机减速概率):更容易引发连锁减速,加剧拥堵。
- 减小v_max(最大速度):道路通行效率降低,易拥堵。
- 扩展方向:
- 加入车道变换、红绿灯、出入口等元素。
- 模拟不同类型车辆(如小汽车、货车)的差异行为。
通过这份代码,可以直观理解微观车辆行为如何通过简单规则演化为宏观堵车现象,是交通流模拟的入门经典案例。
模型代码
