数据结构（19）

目录

内部排序

一、基本概念

二、插入排序

1、直接插入排序

（1）核心思想

（2）具体步骤（示例演示）

（3）算法实现（代码示例）

（4）算法特性

（5）与其他简单排序的对比

2、折半插入排序（顺序表）

（1）核心思想

（2）具体步骤（示例演示）

（3）算法实现（代码示例）

（4）算法特性

（5）与直接插入排序的对比

内部排序

一、基本概念

1、排序：将一组杂乱无章的数据（存放在数据表中）按一定的规律（按关键字）排列起来

2、目的：便于查找

3、衡量排序的好坏：

① 时间效率：排序速度

② 空间效率：占内存辅助空间大小

③ 稳定性：若两个记录A和B的关键字值相等，但排序后A、B的先后次序保持不变，则称这种排序算法是稳定的

4、若待排序记录都在内存中，称为内部排序：

① 顺序排序 —— 排序时直接移动记录

② 链表排序 —— 排序时只移动指针

③ 地址排序 —— 先移动地址，再移动记录（可以增设一维数组来专门存放记录的地址）

5、若待排序记录一部分在内存，一部分在外存，则成为外部排序

二、插入排序

基本思想：每步将一个待排序的对象，按其关键码大小，插入到前面已经排好序的一组对象的适当位置上，直到对象全部插入为止（边插边排序）

1、直接插入排序

直接插入排序（Straight Insertion Sort）是一种简单直观的稳定排序算法，其核心思想是 “将待排序元素逐个插入到已排序序列的合适位置”，类似于玩扑克牌时整理手牌的过程（每次摸一张牌，插入到手中已有序的牌中）。

（1）核心思想

1. 初始状态：将序列的第一个元素视为 “已排序序列”（只有 1 个元素，天然有序）。
2. 逐步插入：从第二个元素开始，依次将每个待插入元素（称为 “关键字”）与已排序序列中的元素从后往前比较，找到其 “在已排序序列中的正确位置” 并插入。
3. 保持有序：插入过程中，已排序序列的元素可能需要向后移动，为待插入元素腾出位置，确保插入后序列依然有序。

（2）具体步骤（示例演示）

例子1：

以排序序列 [5, 3, 8, 4, 2] 为例，步骤如下：

1. 初始状态

已排序序列：[5]（第一个元素），待插入元素：3, 8, 4, 2。

2. 插入第 2 个元素 3

• 比较 3 与已排序序列的最后一个元素 5：3 < 5，将 5 后移一位 → 已排序序列变为 [5, 5]。
• 已排序序列无更多元素，将 3 插入到第一位 → 已排序序列：[3, 5]。

3. 插入第 3 个元素 8

• 比较 8 与已排序序列的最后一个元素 5：8 > 5，无需移动元素，直接插入到末尾 → 已排序序列：[3, 5, 8]。

4. 插入第 4 个元素 4

• 比较 4 与 8：4 < 8，将 8 后移 → [3, 5, 8, 8]。
• 比较 4 与 5：4 < 5，将 5 后移 → [3, 5, 5, 8]。
• 比较 4 与 3：4 > 3，停止比较，插入 4 到 3 之后 → 已排序序列：[3, 4, 5, 8]。

5. 插入第 5 个元素 2

• 比较 2 与 8：2 < 8，8 后移 → [3, 4, 5, 8, 8]。
• 比较 2 与 5：2 < 5，5 后移 → [3, 4, 5, 5, 8]。
• 比较 2 与 4：2 < 4，4 后移 → [3, 4, 4, 5, 8]。
• 比较 2 与 3：2 < 3，3 后移 → [3, 3, 4, 5, 8]。
• 已排序序列无更多元素，插入 2 到第一位 → 最终排序结果：[2, 3, 4, 5, 8]。

例子2：

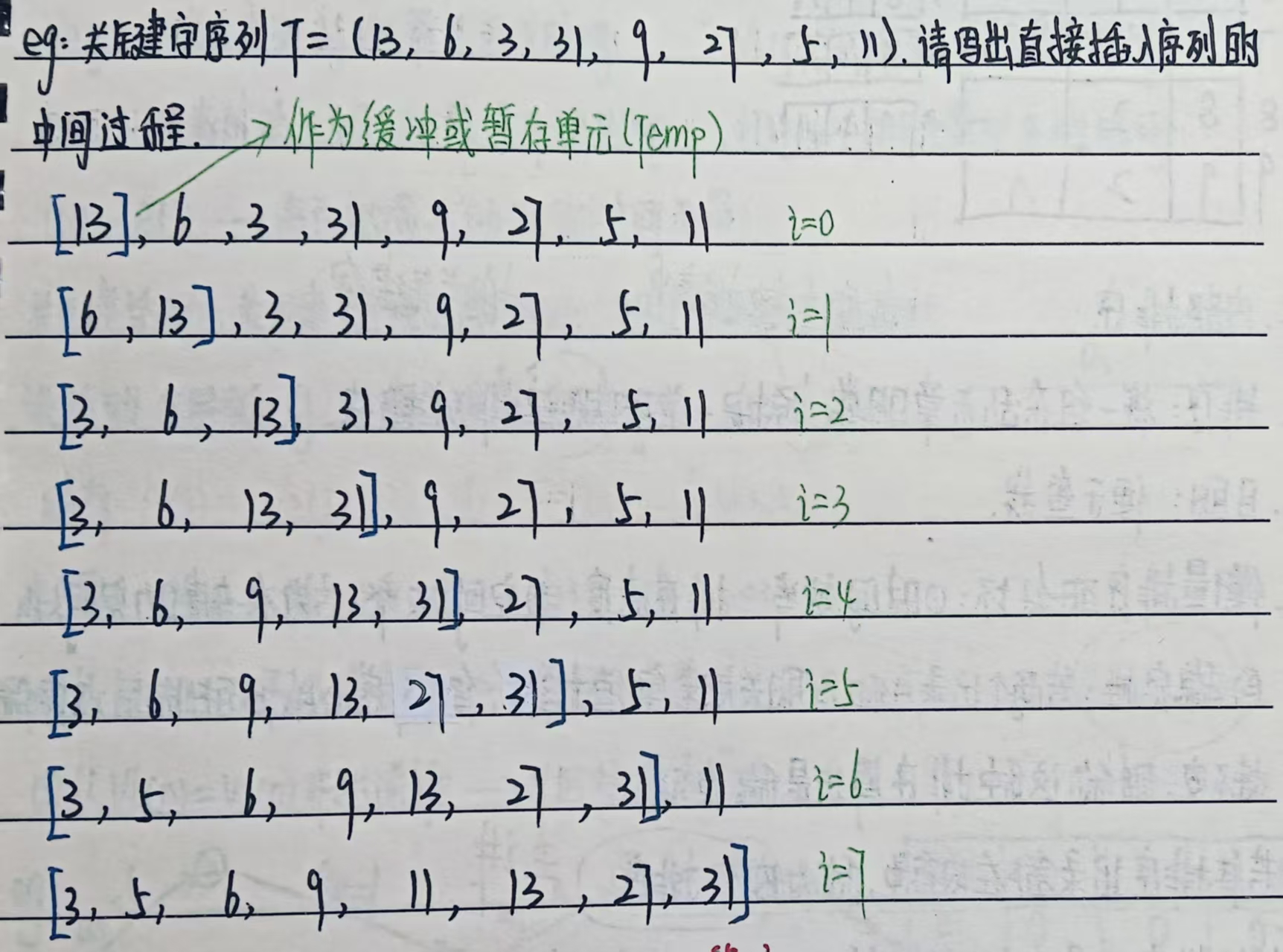
（3）算法实现（代码示例）

def insertion_sort(arr):# 从第二个元素开始遍历（索引1到n-1）for i in range(1, len(arr)):key = arr[i]  # 当前待插入的元素j = i - 1     # 已排序序列的最后一个元素索引# 从后往前比较，将大于key的元素后移while j >= 0 and key < arr[j]:arr[j + 1] = arr[j]  # 元素后移j -= 1# 插入key到正确位置（j+1是插入索引）arr[j + 1] = keyreturn arr# 测试
arr = [5, 3, 8, 4, 2]
print(insertion_sort(arr))  # 输出：[2, 3, 4, 5, 8]

（4）算法特性

1. 时间复杂度：

   • 最佳情况：序列已有序（如 [1,2,3,4]），只需比较 n-1 次，无需移动元素，时间复杂度为 O(n)。
   • 最坏情况：序列逆序（如 [4,3,2,1]），需比较和移动 O(n2) 次，时间复杂度为 O(n2)。
   • 平均情况：时间复杂度为 O(n2)（适用于大多数随机序列）。

2. 空间复杂度：仅需常数级额外空间（存储 key 和索引），空间复杂度为 O(1)（原地排序）。

3. 稳定性：稳定排序。当待插入元素与已排序序列中的元素相等时，会插入到相等元素的后面，保持原有顺序（如 [2, 5, 3, 5] 排序后仍为 [2, 3, 5, 5]，两个 5 的相对位置不变）。

4. 适用场景：

   • 小规模数据排序（因 O(n2) 复杂度在大数据量时效率低）。
   • 接近有序的数据（最佳情况下效率接近 O(n)）。
   • 流式数据（可实时插入新元素并保持有序）。

（5）与其他简单排序的对比

排序算法	时间复杂度（平均）	空间复杂度	稳定性	适用场景
直接插入排序	O(n2)	O(1)	稳定	小规模、接近有序数据
冒泡排序	O(n2)	O(1)	稳定	小规模数据，实现简单
简单选择排序	O(n2)	O(1)	不稳定	对稳定性无要求的场景

直接插入排序的优势在于：对接近有序的数据效率极高，且实际运行中比冒泡排序和简单选择排序更快（比较和移动操作更少）。

直接插入排序是一种 “增量式构建有序序列” 的算法，通过逐个插入元素并保持有序，实现简单且稳定。尽管在大数据量下效率较低，但其对小规模或接近有序数据的高效性，使其在实际场景中仍有广泛应用（如数据库索引排序、日常数据整理等）。

2、折半插入排序（顺序表）

折半插入排序（Binary Insertion Sort）是对直接插入排序的优化，适用于顺序表（数组）结构。它在 “寻找待插入元素的正确位置” 时，用折半查找（二分查找） 替代直接插入排序的 “顺序查找”，减少了比较次数，从而提升效率（尤其在数据量较大时）。核心思想仍是 “将待排序元素插入到已排序序列的合适位置”，但优化了查找位置的过程。

（1）核心思想

1. 初始状态：同直接插入排序，将序列第一个元素视为 “已排序序列”。
2. 折半查找位置：对每个待插入元素（从第二个元素开始），在已排序序列中用折半查找找到其插入位置（即第一个大于待插入元素的位置）。
3. 元素后移与插入：将已排序序列中 “插入位置及之后的元素” 统一后移一位，再将待插入元素放入该位置，保持序列有序。

（2）具体步骤（示例演示）

以排序序列 [5, 3, 8, 4, 2] 为例，步骤如下：

1. 初始状态

已排序序列：[5]（索引 0），待插入元素：3（索引 1）、8（索引 2）、4（索引 3）、2（索引 4）。

2. 插入第 2 个元素 3（索引 1）

• 折半查找插入位置：已排序序列范围 [0,0]（low=0，high=0）。中间索引 mid = (0+0)//2 = 0，比较 3 与 arr[0]=5：3 < 5，说明插入位置在 mid 左侧，调整 high = mid - 1 = -1。查找结束，插入位置为 low=0（当 high < low 时，low 即为插入索引）。
• 元素后移与插入：将索引 0 的元素 5 后移到索引 1，再将 3 插入索引 0 → 已排序序列：[3, 5]。

3. 插入第 3 个元素 8（索引 2）

• 折半查找插入位置：已排序序列范围 [0,1]（low=0，high=1）。mid = (0+1)//2 = 0，比较 8 与 arr[0]=3：8 > 3，调整 low = mid + 1 = 1。新范围 [1,1]，mid=1，比较 8 与 arr[1]=5：8 > 5，调整 low = mid + 1 = 2。查找结束，插入位置为 low=2（超出已排序序列末尾）。
• 直接插入：无需后移元素，8 插入索引 2 → 已排序序列：[3, 5, 8]。

4. 插入第 4 个元素 4（索引 3）

• 折半查找插入位置：已排序序列范围 [0,2]（low=0，high=2）。mid=1，比较 4 与 arr[1]=5：4 < 5，调整 high = 0。新范围 [0,0]，mid=0，比较 4 与 arr[0]=3：4 > 3，调整 low = 1。查找结束，插入位置为 low=1。
• 元素后移与插入：将索引 1、2 的元素 5,8 后移到索引 2、3，4 插入索引 1 → 已排序序列：[3, 4, 5, 8]。

5. 插入第 5 个元素 2（索引 4）

• 折半查找插入位置：已排序序列范围 [0,3]（low=0，high=3）。mid=1，比较 2 与 arr[1]=4：2 < 4，调整 high=0。mid=0，比较 2 与 arr[0]=3：2 < 3，调整 high=-1。查找结束，插入位置为 low=0。
• 元素后移与插入：将索引 0-3 的元素 3,4,5,8 后移到索引 1-4，2 插入索引 0 → 最终序列：[2, 3, 4, 5, 8]。

（3）算法实现（代码示例）

def binary_insertion_sort(arr):for i in range(1, len(arr)):key = arr[i]  # 待插入元素low = 0       # 已排序序列的起始索引high = i - 1  # 已排序序列的结束索引# 折半查找插入位置（low最终为插入索引）while low <= high:mid = (low + high) // 2if key < arr[mid]:high = mid - 1  # 插入位置在mid左侧else:low = mid + 1  # 插入位置在mid右侧（含mid）# 将插入位置及之后的元素后移for j in range(i, low, -1):arr[j] = arr[j - 1]# 插入待排序元素arr[low] = keyreturn arr# 测试
arr = [5, 3, 8, 4, 2]
print(binary_insertion_sort(arr))  # 输出：[2, 3, 4, 5, 8]

（4）算法特性

1. 时间复杂度：

   • 比较次数：折半查找的时间复杂度为 O(logk)（k 为已排序序列长度），n 个元素的总比较次数为 O(nlogn)（优于直接插入排序的 O(n2)）。
   • 移动次数：与直接插入排序相同，最坏和平均情况仍为 O(n2)（元素后移操作无法避免）。
   • 整体复杂度：仍为 O(n2)（受限于移动次数），但实际效率优于直接插入排序（比较次数减少）。

2. 空间复杂度：仅需常数级额外空间（存储 key、low、high 等），空间复杂度为 O(1)（原地排序）。

3. 稳定性：稳定排序。折半查找时，若待插入元素与已排序元素相等，会插入到相等元素的后面（因 key >= arr[mid] 时调整 low = mid + 1），保持原有顺序。

4. 适用场景：

   • 顺序表（数组）结构（需随机访问元素，支持折半查找）。
   • 数据量较大且接近无序的场景（相比直接插入排序，减少比较次数的优势更明显）。
   • 不适用于链表（链表无法高效进行随机访问，折半查找无意义）。

（5）与直接插入排序的对比

对比维度	直接插入排序	折半插入排序
查找位置方式	顺序查找（从后往前比较）	折半查找（二分法定位）
比较次数	O(n2)	O(nlogn)
移动次数	O(n2)	O(n2)
整体时间复杂度	O(n2)	O(n2)
适用数据结构	数组、链表	仅数组（顺序表）
实际效率（相同数据）	较低（比较次数多）	较高（比较次数少）

折半插入排序通过 “折半查找优化位置定位”，减少了插入过程中的比较次数，是对直接插入排序的有效改进。尽管整体时间复杂度仍为 O(n2)，但在数据量较大时，其实际运行效率明显高于直接插入排序，尤其适合顺序表结构和需要减少比较操作的场景。