OpenCV(二十三):透视变换
基本概念
1. 仿射变换 vs 透视变换
| 类型 | 数学关系 | 自由度 | 特征 |
|---|---|---|---|
| 仿射变换(Affine) | 保持平行性(平行线仍平行) | 6 参数 | 无透视感 |
| 透视变换(Perspective / Homography) | 保持直线但不保持平行性 | 8 参数 | 具备“投影”与“深度感” |
2. 数学模型(齐次坐标表示)
在透视变换中,点的映射关系为:

其中 H 是一个 3×3 单应性矩阵(Homography Matrix):
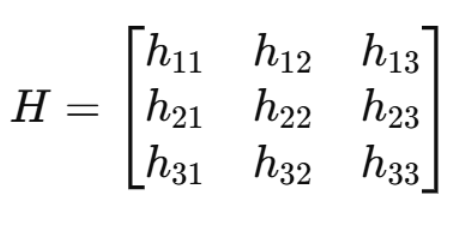
映射到普通坐标(除以最后一维):
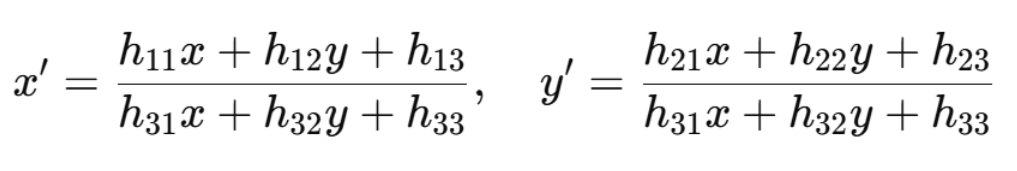
与仿射变换的最大区别:分母含有 x,y,导致远近缩放(透视感)。
3. 自由度(Degrees of Freedom)
- 一个 3×3 的 H 矩阵有 9 个参数;
- 由于任意比例因子不影响结果(乘以常数等价),所以只有 8 个有效自由度;
- 每个点提供两个约束(x’, y’);
- 因此至少需要 4 对匹配点 来求解 H。
透视变换的求解原理
给定四对点:
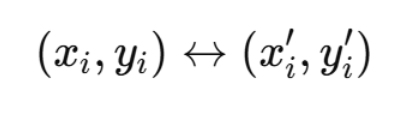
每一对点可得两个线性方程:
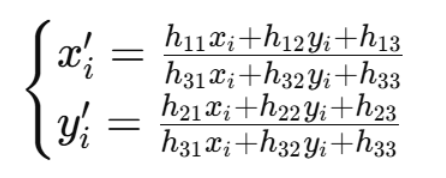
整理为线性方程组:
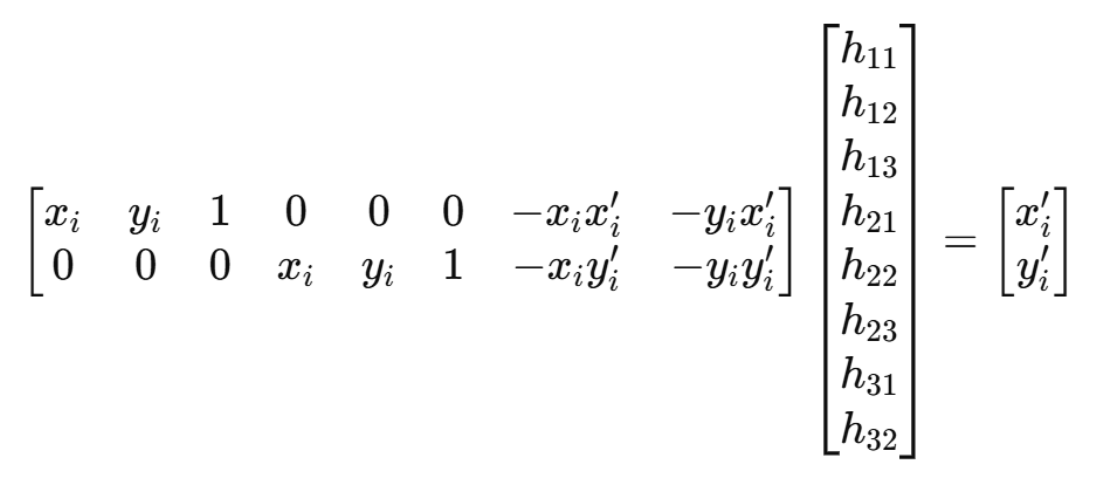
解出 H(8 个未知数 + 固定 h33=1)。
OpenCV 的 cv2.getPerspectiveTransform() 内部就是解这个方程组。
warpPerspective 内部工作机制
1. 逆向映射(Inverse Mapping)
对输出图像中每个像素 (x′,y′),根据矩阵 H 计算原图位置:
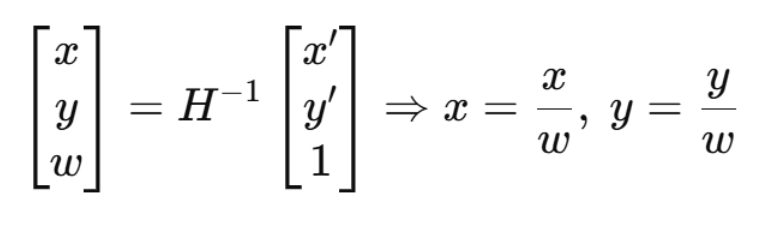
再根据 (x, y) 在原图采样(插值)。
2. 插值方式
通过 interpolation 参数控制:
| 插值方法 | 参数 | 特点 |
|---|---|---|
| 最近邻 | cv2.INTER_NEAREST | 速度快,可能锯齿 |
| 双线性 | cv2.INTER_LINEAR | 默认,平滑自然 |
| 双三次 | cv2.INTER_CUBIC | 高质量,速度慢 |
| Lanczos | cv2.INTER_LANCZOS4 | 超高质量,适合矫正文档 |
3. 边界处理
borderMode 控制越界像素的填充:
| 参数 | 含义 |
|---|---|
cv2.BORDER_CONSTANT | 填充固定值 |
cv2.BORDER_REPLICATE | 复制边缘 |
cv2.BORDER_REFLECT | 镜像反射 |
OpenCV 实现流程
OpenCV 提供两个核心函数:
| 函数 | 功能 |
|---|---|
cv2.getPerspectiveTransform(src, dst) | 根据四对点计算 3×3 透视变换矩阵 H |
cv2.warpPerspective(image, H, dsize) | 根据 H 对图像进行透视变换 |
示例:透视变换 + 图像校正
import cv2
import numpy as np
import matplotlib.pyplot as plt# 中文显示支持
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 读取图像
img = cv2.imread('document.jpg')
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)h, w = img.shape[:2]
print("原始图像大小:", (w, h))# Step 1: 定义原图四个顶点
# 假设图像中心偏上、倾斜一点的文档区域(单位为像素)
src_pts = np.float32([[0.25*w, 0.2*h], # 左上[0.75*w, 0.18*h], # 右上[0.8*w, 0.8*h], # 右下[0.2*w, 0.85*h] # 左下
])# Step 2: 目标矩形区域大小(比如想拉正为 400x600)
dst_width, dst_height = 400, 600
dst_pts = np.float32([[0, 0],[dst_width, 0],[dst_width, dst_height],[0, dst_height]
])# Step 3: 计算透视变换矩阵
M = cv2.getPerspectiveTransform(src_pts, dst_pts)# Step 4: 执行透视变换
warped = cv2.warpPerspective(img, M, (dst_width, dst_height))# Step 5: 可视化结果
plt.figure(figsize=(10,6))# 原图
plt.subplot(1,2,1)
plt.imshow(img)
plt.title('原始图像')
for p in src_pts:plt.scatter(p[0], p[1], c='r', s=40)
plt.axis('off')# 透视变换后
plt.subplot(1,2,2)
plt.imshow(warped)
plt.title('透视变换后')
plt.axis('off')plt.tight_layout()
plt.show()
执行效果:

总结
| 步骤 | 数学原理 | 实现函数 | 备注 |
|---|---|---|---|
| 建立点对 | 平面到平面映射 | 手动或检测特征点 | 至少 4 对 |
| 求解矩阵 H | 齐次线性方程组(DLT算法) | cv2.getPerspectiveTransform() / cv2.findHomography() | findHomography 支持鲁棒估计(RANSAC) |
| 执行变换 | 逆向映射 + 插值 | cv2.warpPerspective() | 支持多种插值和边界模式 |
| 可逆 | H 的逆矩阵 | np.linalg.inv(H) | 可映射回原图 |
