简单理解：ADC（模数转换）采集的滤波算法

 

 

 

 

 

 

ADC（模数转换）采集的滤波算法，核心是滤除采样噪声（如工频干扰、随机噪声）、提升数据稳定性，以下是常用算法+核心特点+适用场景，极简好懂：

1. 滑动平均滤波（Moving Average）

    •    核心：取连续N个采样值的平均值作为有效输出（比如N=5，每次取最新5个值求平均）。

    •    优点：简单易实现、计算量小，能滤除高频随机噪声；缺点：对突发信号（如尖峰干扰）抑制差，N越大响应越慢。

    •    适用：采样频率高、噪声平稳的场景（如温度、湿度缓慢变化的模拟量采集）。

2. 加权滑动平均滤波

    •    核心：在滑动平均基础上，给近期采样值赋更高权重（比如最新值权重0.5，前1个0.3，前2个0.2），再求和输出。

    •    优点：兼顾平滑噪声和快速响应，比普通滑动平均更灵活；缺点：需手动调整权重，适配性依赖经验。

    •    适用：既需要降噪，又不能容忍大幅延迟的场景（如轻度波动的电压采集）。

3. 中值滤波（Median Filter）

    •    核心：取连续N个采样值排序后，取中间值作为输出（比如N=5，排序后第3个值）。

    •    优点：对尖峰干扰（如静电脉冲、突发抖动）抑制极强，不影响信号趋势；缺点：对高频噪声滤除效果一般，N越大延迟越大。

    •    适用：存在突发干扰的场景（如工业现场的电流采集、传感器接触抖动）。

4. 一阶滞后滤波（RC数字滤波）

    •    核心：按公式计算：Y(n) = α×X(n) + (1-α)×Y(n-1)（X为当前采样值，Y为上一次输出值，α是0~1的权重系数）。

    •    优点：兼顾平滑性和响应速度，α越大响应越快、平滑越弱，反之则相反；缺点：α需反复调试，对大幅突变信号跟踪差。

    •    适用：高频噪声多、信号有小幅波动的场景（如压力、液位采样）。

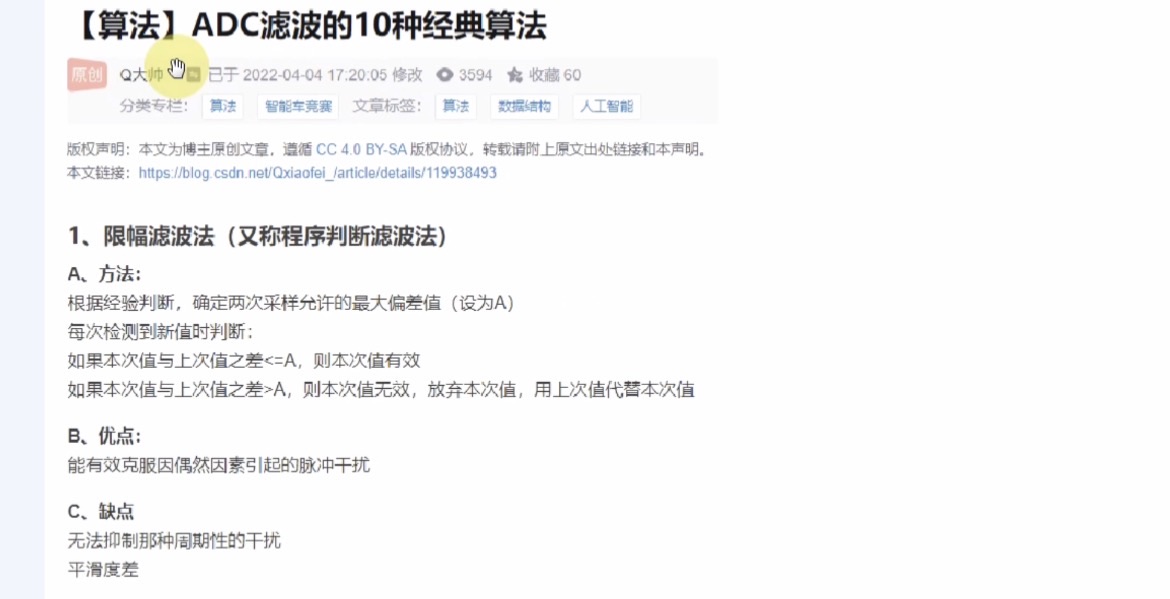
5. 限幅滤波（Clipping Filter）

    •    核心：设定采样值的合理范围（上限Vmax、下限Vmin），超出范围则丢弃，沿用上次有效值。

    •    优点：能快速剔除异常极值（如采样错误、大幅干扰），计算量极小；缺点：无法滤除范围内的噪声，需配合其他算法使用。

    •    适用：易出现极端异常值的场景（如户外传感器、电磁干扰强的环境）。

6. 卡尔曼滤波（Kalman Filter）

    •    核心：通过“预测-更新”迭代，结合信号模型和噪声统计特性，动态估算最优值（需建立系统方程）。

    •    优点：降噪效果优、能处理非线性/动态信号，适合复杂噪声环境；缺点：数学模型复杂、计算量大，需调试参数（Q/R矩阵）。

    •    适用：高精度、复杂噪声的场景（如惯性导航、电机转速采集、高精度电压监测）。

核心选型原则

    •    简单场景（低精度、慢变化）：滑动平均、限幅滤波（低成本、易实现）；

    •    突发干扰场景：中值滤波（优先扛尖峰）；

    •    兼顾响应与平滑：加权滑动平均、一阶滞后（手动调参数）；

    •    高精度/复杂噪声：卡尔曼滤波（需投入建模成本）。