算法30.0

560. 和为 K 的子数组 - 力扣（LeetCode）

---

自己的理解：

为什么不能用滑动窗口？

虽然left指针和right指针都是同向移动   但是因为本题目有负数的情况 导致同向移动会漏掉情况

right往右走  当满足窗口条件（和为k） 的时候  left也不能右移  因为后面说不定还有情况 

所以其实不是同向移动的  （下面的第一张图片里面介绍了这种情况） 

不具备单调性就不能用双指针优化

为什么要以i位置为结尾的和？

减少时间复杂度？   

为什么需要借助哈希表？

第二次迭代优化的时候 那三种细节问题？

---

细节：

审题：nums是 1 2 3 ， k = 3 的时候  单独一个3也是nums的子数组

这道题目中数组里面的子数组是既有正数也有负数的   完完整整的做

把数组抽象成一条横线 这个是抽象化的一种习惯方式  

---

别人的讲解：

暴力解法：关于子数组的解法 就是暴力枚举策略  时间复杂度是：n的平方

一直向后加  得到结果是k就返回  继续加（有负数的情况） 

不能用双指针（滑动窗口）是因为这里的

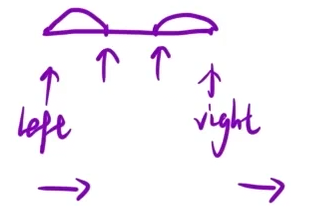
优化暴力解法：这道题目是需要求出某个区间的和 可以试试前缀和

以i位置为结尾的所有的子数组（和暴力解法挂钩 暴力解法是以i位置为开头的子数组）  

这样也是可以枚举所有子数组

当我枚举到i位置之后  我们已经知道了 以i位置为结尾的区间的和(前缀和的功劳）

这道题就转化为了  以下：

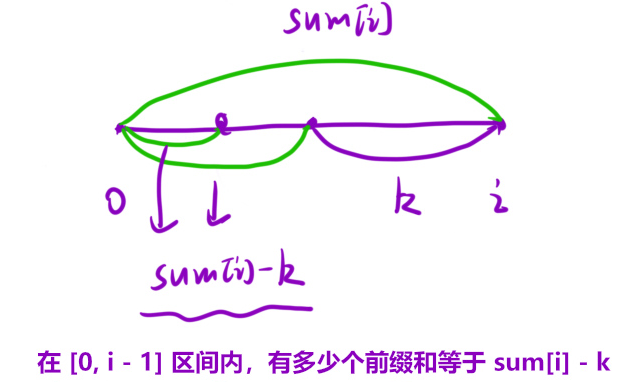
找到某个区间的和是sum i - k   这样也找到了后面那个区间和是k的子区间了 （绿线是前缀和） 

这样的算法时间复杂度还不如暴力解法   （从头到位遍历一遍数组  有多少个前缀和等于sum i - k

依旧是遍历一遍    还比暴力解法需要多出来的预处理的一步

如何快速和的找到前缀和有多少个等于k 

继续优化：这个需要借助哈希表  存两个int 一个是前缀和 一个是前缀和出现的次数

这样会出现各种细节问题：

//前缀和加入哈希表的时机？  两种加入的时机  算出所有前缀和 然后加入进去  

不能直接把前缀和全丢入到哈希表  如果这样的话  i后面的情况也遍历到了

优化是：在计算i位置之前，哈希表里面只保存0到i-1位置的前缀和

//不用真的创建一个前缀和数组  我们仅需用一个变量比较一下i位置之前的那些元素的前缀和是多少  

//如何整个前缀和等于k呢？ 

先把 hash 0 =1 丢入数组 避免整个数组为k（这个时候需要前缀和为0  不存在） 

---

下面是题目、效果图和代码：

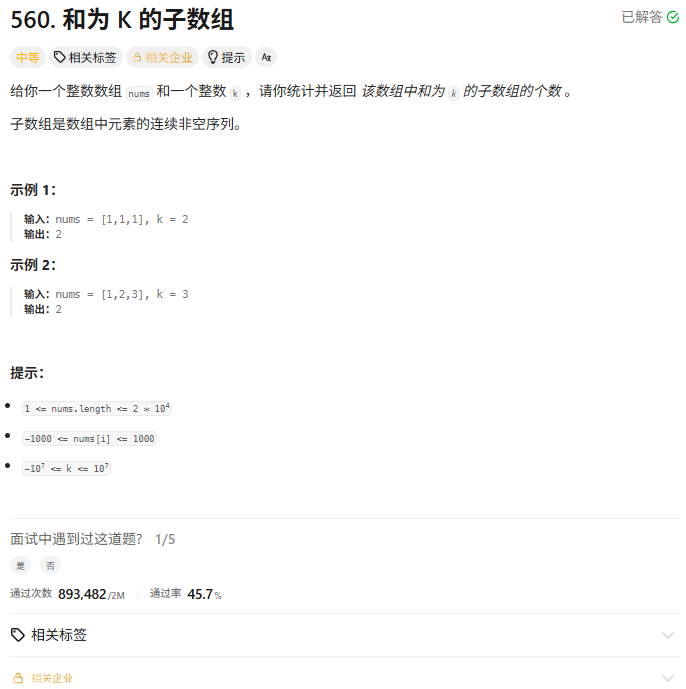
class Solution 
{public int subarraySum(int[] nums, int k) {Map<Integer,Integer> hash = new HashMap<Integer,Integer>();hash.put(0,1);int sum = 0 , ret = 0;for(int x : nums){sum += x ; //计算当前位置的前缀和ret += hash.getOrDefault(sum - k,0);//统计结果hash.put(sum,hash.getOrDefault(sum,0)+1); // 把当前的前缀和丢到哈希表里面}return ret ;}
}
//xiyu251109&1#4*5