分治归并算法第一弹
目录
前言
1、归并排序
1.1 归并简述
1.2 归并题解
2. 交易中的逆序对
2.1 题目及示例
2.2 解题思路
2.3 题解代码
3. 计算右侧小于当前元素的个数
3.1 题目及示例
3.2 解题思路
3.3 题解代码
前言
本文以三道题目为例,讲解了分治归并算法,希望对你有所帮助!
1、归并排序
1.1 归并简述
归并排序(MergeSort)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
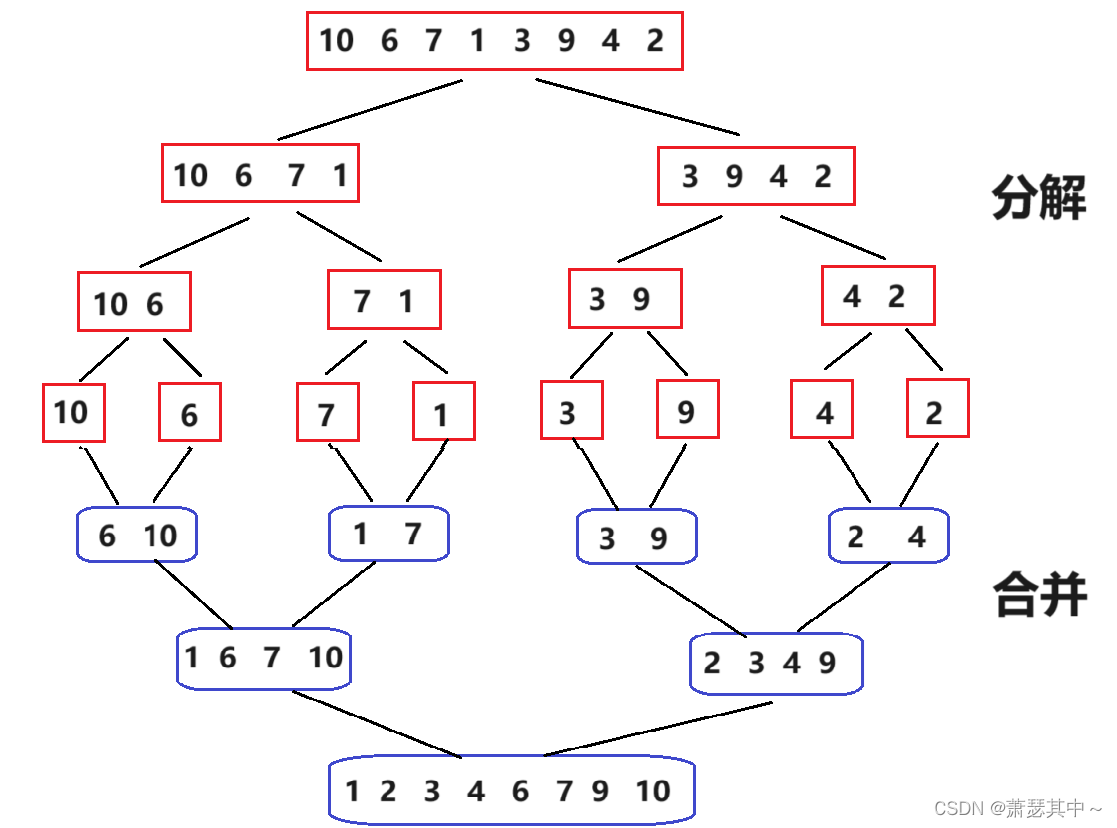
归并排序充分体现了分治-归并的思想。
1.2 归并题解
题目链接:https://leetcode.cn/problems/sort-an-array/description/
给你一个整数数组
nums,请你将该数组升序排列。你必须在 不使用任何内置函数 的情况下解决问题,时间复杂度为
O(nlog(n)),并且空间复杂度尽可能小。
示例 1:
输入:nums = [5,2,3,1]
输出:[1,2,3,5]
解释:数组排序后,某些数字的位置没有改变(例如,2 和 3),而其他数字的位置发生了改变(例如,1 和 5)。
示例 2:
输入:nums = [5,1,1,2,0,0]
输出:[0,0,1,1,2,5]
解释:请注意,nums 的值不一定唯一。
这里采用递归版本的归并排序
vector<int> sortArray(vector<int>& nums) {mergeSort(nums, 0, nums.size() - 1);return nums;}void mergeSort(vector<int>& nums, int begin, int end){if (begin >= end)return;// 1.根据中间元素,划分区间int mid = (begin + end) >> 1;// 2.分为两部分[begin, mid] [mid+1, end]mergeSort(nums, begin, mid);mergeSort(nums, mid + 1, end);vector<int> tmp(end - begin + 1);// 3.合并处理int cur1 = begin, cur2 = mid + 1, i = 0;while (cur1 <= mid && cur2 <= end) tmp[i++] = nums[cur1] > nums[cur2] ? nums[cur2++] : nums[cur1++];// 4.处理多余的数while (cur1 <= mid) tmp[i++] = nums[cur1++];while (cur2 <= end) tmp[i++] = nums[cur2++];// 5.还原for (int k = begin; k <= end; k++){nums[k] = tmp[k - begin];}}2. 交易中的逆序对
2.1 题目及示例
题目链接:https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/description/
在股票交易中,如果前一天的股价高于后一天的股价,则可以认为存在一个「交易逆序对」。请设计一个程序,输入一段时间内的股票交易记录 record,返回其中存在的「交易逆序对」总数。
示例 1:
输入:record = [9, 7, 5, 4, 6]
输出:8
解释:交易中的逆序对为 (9, 7), (9, 5), (9, 4), (9, 6), (7, 5), (7, 4), (7, 6), (5, 4)。
提示:0 <= record.length <= 50000
2.2 解题思路
我们可以尝试使用分治归并的思想来解题。如下图:
- 一开始对这个数组进行分解,直到分解成每个子数组中只包含一个元素。对于归并排序来说,此时需要合并。
- 但是这道题目需要计算逆序对个数,我们可以在两个子数组合并过程中,利用子数组的有序性,选出逆序对。
- 合并的过程中,每一步都可以挑选出逆序对,只需要将每一步逆序对数量加起来,就是题目的答案。
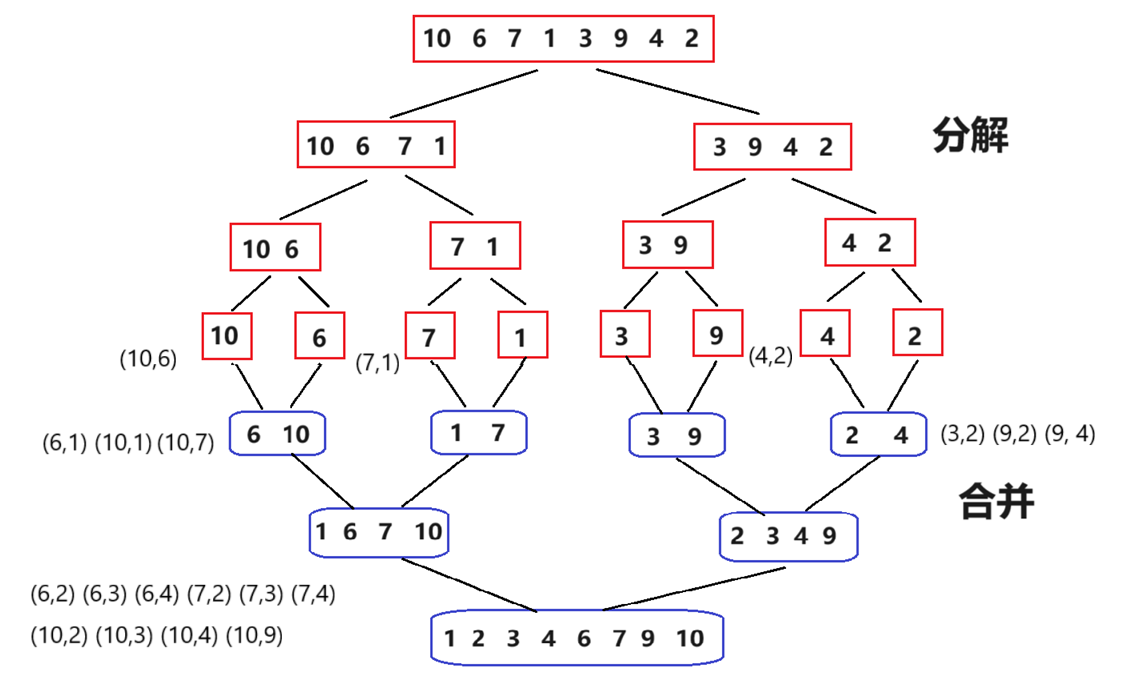
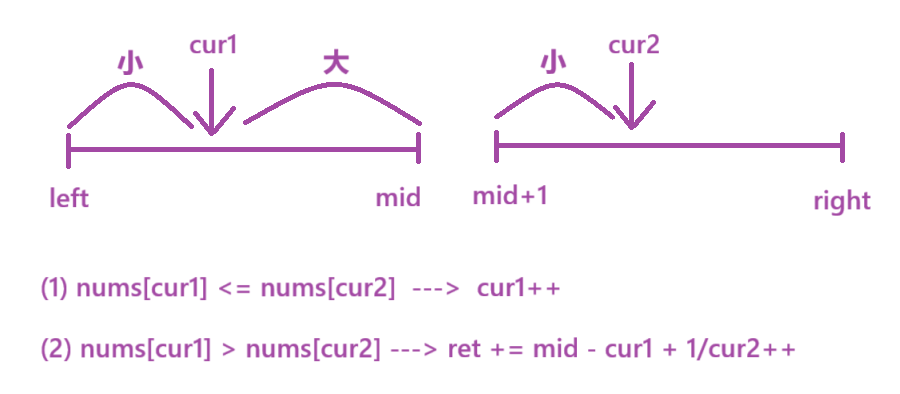
如下图,我们进一步抽象,将下面的两条线段当做准备合并的两个子数组:
- cur1和cur2指针执行归并排序中的合并操作。
- 此时,采用的是升序策略,所以cur1指向的元素左边都是较小元素,右边都是较大元素。
- 当cur1指向的元素小于等于cur2指向的元素,cur1左边的元素肯定比cur2指向元素更小,形成不了逆序对。cur1右边的元素可能有比cur2指向的元素更大。无法确定逆序对元素个数,所以只执行cur1++的操作。
- 当cur1指向的元素大于cur2指向的元素,cur1右边的元素肯定比cur2指向的元素更大,所以逆序对个数ret,可以加等上cur1到mid区间的长度,再执行cur2++的操作。
2.3 题解代码
题目中的提示,指出给定数组元素个数区间在[0,50000]。因此,我们可以定义一个固定为50001的整型数组。
class Solution {int tmp[50001];int _n;
public:int reversePairs(vector<int>& record) {_n = record.size();return mergeSort(record, 0, _n - 1);}int mergeSort(vector<int>& nums, int begin, int end){if (begin >= end)return 0;int ret = 0;// 1.根据中间元素,划分区间int mid = (begin + end) >> 1;// [begin, mid] [mid+1, end]// 2.先处理左右两部分ret += mergeSort(nums, begin, mid);ret += mergeSort(nums, mid + 1, end);// 3.处理一左一右的情况int cur1 = begin, cur2 = mid + 1, i = 0;while (cur1 <= mid && cur2 <= end) {if (nums[cur1] <= nums[cur2]) {tmp[i++] = nums[cur1++];} else {ret += mid - cur1 + 1;tmp[i++] = nums[cur2++];}}// 4.处理剩下的排序过程while (cur1 <= mid) {tmp[i++] = nums[cur1++];}while (cur2 <= end) {tmp[i++] = nums[cur2++];}// 还原for (int k = begin; k <= end; k++){nums[k] = tmp[k - begin];}return ret;}
};3. 计算右侧小于当前元素的个数
3.1 题目及示例
题目链接:https://leetcode.cn/problems/count-of-smaller-numbers-after-self/description/
给你一个整数数组 nums ,按要求返回一个新数组 counts 。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
提示:1 <= nums.length <= 105 -104 <= nums[i] <= 104
示例 1:
输入:nums = [5,2,6,1]
输出:[2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素
示例 2:
输入:nums = [-1]
输出:[0]
示例 3:
输入:nums = [-1,-1]
输出:[0,0]
3.2 解题思路
这道题目求解的是每个元素对应的逆序对个数,不是逆序对总数,并且要求最后按照原来下标存放每个元素元素的逆序对个数。
- 合并排序的过程中,我们会使用新数组存放合并排序的结果,再把该结果拷贝会原数组。
- 因为我们得清楚每个元素的初始下标,所以我们还需要定义一个tmpIndex,tmpIndex[i]就表示合并后,在i下标的元素的初始下标值。并且一开始要对tmpIndex初始化,使得tmpIndex[i] = i
- 所以,每次合并排序需要更新两个数组。
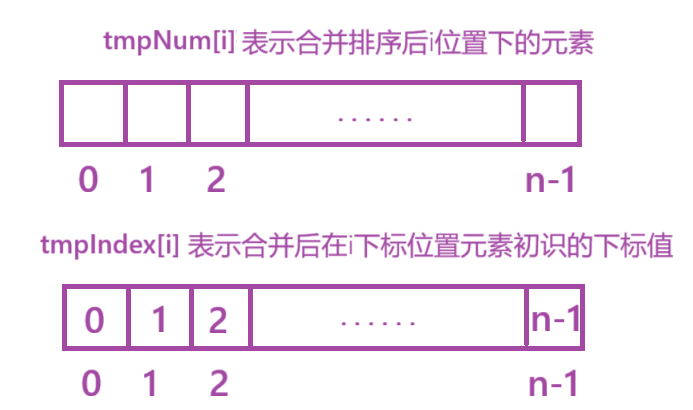
这次是降序排序,使用的策略是找出i位置元素后面比nums[i]的元素个数。分析思路跟上题类似。
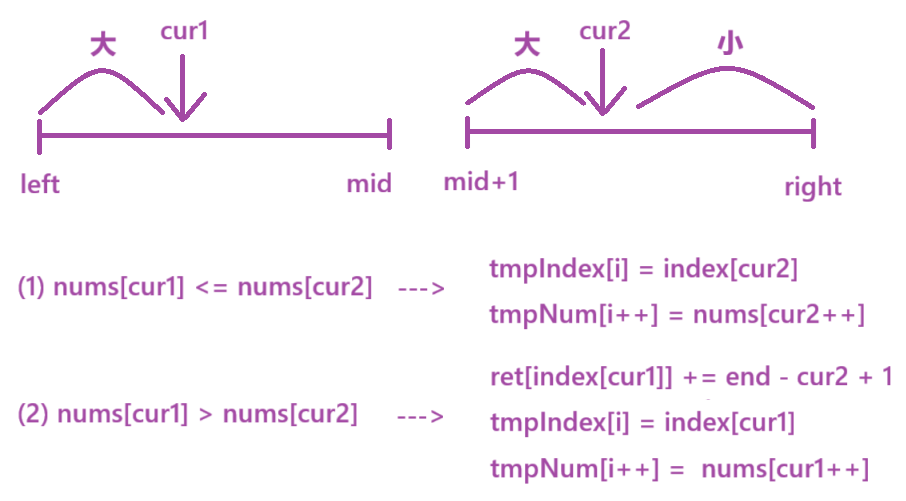
- 当nums[cur1]小于等于nums[cur2],cur2左边的元素肯定比cur1所在元素大,而cur2右侧的元素不能确定是否比cur1所在元素的大小,所以更新tmpIndex和tmpNum两个数组。
- 当nums[cur1]大于等于nums[cur2],cur2右边的元素肯定小于cur1所在的元素。创建一个ret数组,在index[cur1]]下标下,加上end - cur2 + 1的数值。继续更新tmpIndex和tmpNum两个数组。
3.3 题解代码
题目中的提示,指出给定数组元素个数区间在[0,200000]。因此,我们可以定义两个固定为200001的整型数组,分表是tmpNum和tmpIndex。
class Solution {vector<int> ret;vector<int> index;int tmp[200000];int tmpIndex[200000];int _n;
public:vector<int> countSmaller(vector<int>& nums) {_n = nums.size();ret.resize(_n, 0);index.resize(_n, 0);for (int i = 1; i < _n; i++){index[i] = i;}mergeSort(nums, 0, _n - 1);return ret;}void mergeSort(vector<int>& nums, int begin, int end){if (begin >= end)return;// 1.根据中间元素,划分区间int mid = (begin + end) >> 1;// [begin, mid] [mid+1, end]// 2.先处理左右两部分mergeSort(nums, begin, mid);mergeSort(nums, mid + 1, end);// 3.处理一左一右的情况int cur1 = begin, cur2 = mid + 1, i = 0;while (cur1 <= mid && cur2 <= end) {if (nums[cur1] <= nums[cur2]) {tmpIndex[i] = index[cur2]; tmp[i++] = nums[cur2++];} else {ret[index[cur1]] += end - cur2 + 1;tmpIndex[i] = index[cur1];tmp[i++] = nums[cur1++];}}// 4.处理剩下的排序过程while (cur1 <= mid) {tmpIndex[i] = index[cur1];tmp[i++] = nums[cur1++];}while (cur2 <= end) {tmpIndex[i] = index[cur2]; tmp[i++] = nums[cur2++];}// 还原for (int k = begin; k <= end; k++){nums[k] = tmp[k - begin];index[k] = tmpIndex[k - begin];}}
};创作充满挑战,但若我的文章能为你带来一丝启发或帮助,那便是我最大的荣幸。如果你喜欢这篇文章,请不吝点赞、评论和分享,你的支持是我继续创作的最大动力!

