线性代数 - 理解特征值和特征向量(Eigenvalue Eigenvector)
线性代数 - 理解特征值和特征向量(Eigenvalue & Eigenvector)
flyfish
原点(0,0)(0,0)(0,0),L位于(4,4)(4,4)(4,4)(向量表示为<4,4><4,4><4,4>)
E位于(8,8)(8,8)(8,8)(向量表示为<8,8><8,8><8,8>),
通过空间位置直观展示“共线向量的缩放关系”,为理解特征值、特征向量做铺垫。
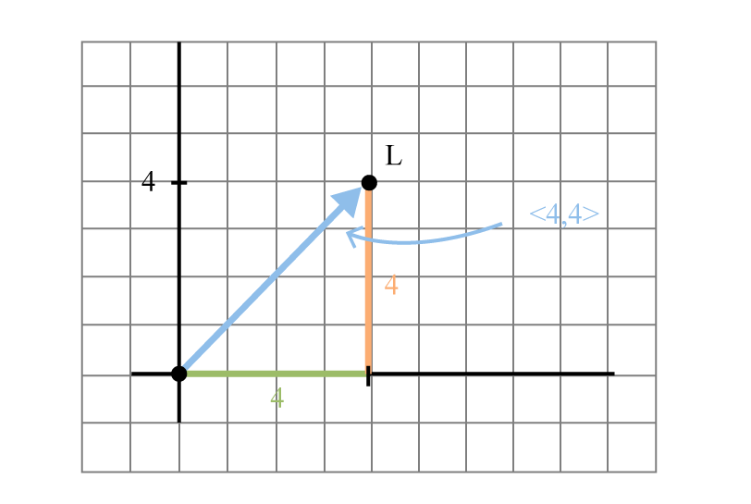
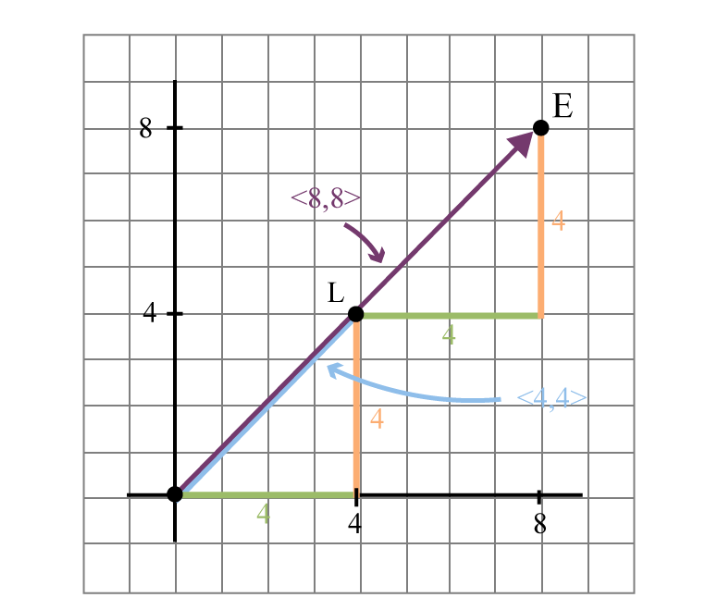
从原点到E的向量<8,8><8,8><8,8>是“原点到L”向量<4,4><4,4><4,4>的2倍,其中“缩放因子2”是特征值,向量<4,4><4,4><4,4>是特征向量。
对于n×nn \times nn×n矩阵AAA,非零向量x⃗\vec{x}x满足Ax⃗=λx⃗A\vec{x} = \lambda \vec{x}Ax=λx时,x⃗\vec{x}x称为特征向量,标量λ\lambdaλ称为特征值。
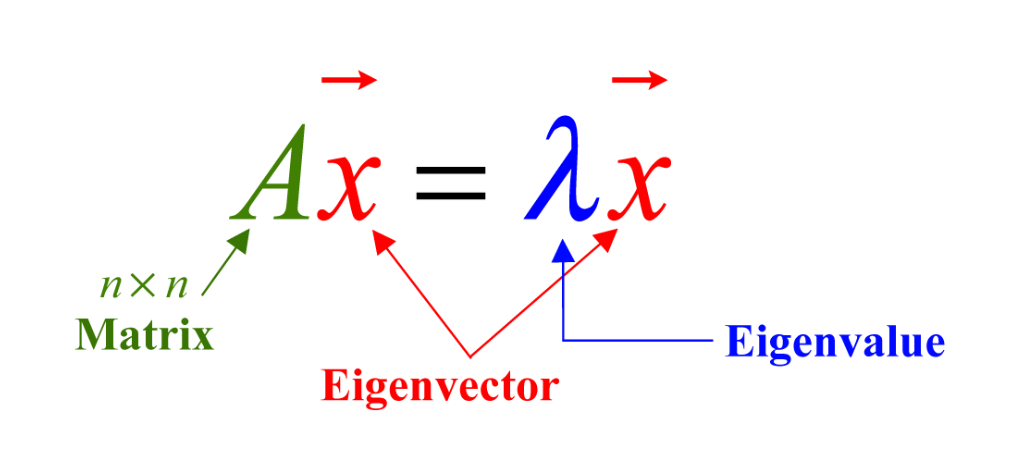
仅方阵存在特征值和特征向量;
特征向量是非零向量,特征值可以是任意实数(包括0);
特征向量Ax⃗A\vec{x}Ax与原向量x⃗\vec{x}x、原点共线(即变换后方向不变,仅长度缩放)。
德语中“eigen”意为“自身”或“特征”,因此特征向量是满足 “经某矩阵(对应线性变换)变换后,结果等于特征向量自身乘以一个固定常数(即特征值)” 的非零向量。
示例:
给定矩阵A=[3−210]A = \begin{bmatrix} 3 & -2 \\ 1 & 0 \end{bmatrix}A=[31−20],验证向量u⃗=[21]\vec{u} = \begin{bmatrix} 2 \\ 1 \end{bmatrix}u=[21]和v⃗=[−11]\vec{v} = \begin{bmatrix} -1 \\ 1 \end{bmatrix}v=[−11]是否为特征向量:
矩阵与向量定义
A=[3−210],u⃗=[21],v⃗=[−11]A = \begin{bmatrix} 3 & -2 \\ 1 & 0 \end{bmatrix}, \quad \vec{u} = \begin{bmatrix} 2 \\ 1 \end{bmatrix}, \quad \vec{v} = \begin{bmatrix} -1 \\ 1 \end{bmatrix} A=[31−20],u=[21],v=[−11]
验证 u ⃗ \vec{u} u是否为特征向量
[3−210]⏟A[21]⏟u=λ[21]⏟u\underbrace{\begin{bmatrix} 3 & -2 \\ 1 & 0 \end{bmatrix}}_{A} \underbrace{\begin{bmatrix} 2 \\ 1 \end{bmatrix}}_{u} \stackrel{}{=} \lambda \underbrace{\begin{bmatrix} 2 \\ 1 \end{bmatrix}}_{u} A[31−20]u[21]=λu[21]
[3−210][21]=[42]=2⏟λ[21]\begin{bmatrix} 3 & -2 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 2 \\ 1 \end{bmatrix} = \begin{bmatrix} 4 \\ 2 \end{bmatrix} = \underbrace{2}_{\lambda} \begin{bmatrix} 2 \\ 1 \end{bmatrix} [31−20][21]=[42]=λ2[21]
验证 v ⃗ \vec{v} v是否为特征向量
[3−210]⏟A[−11]⏟v=λ[−11]⏟v\underbrace{\begin{bmatrix} 3 & -2 \\ 1 & 0 \end{bmatrix}}_{A} \underbrace{\begin{bmatrix} -1 \\ 1 \end{bmatrix}}_{v} \stackrel{}{=} \lambda \underbrace{\begin{bmatrix} -1 \\ 1 \end{bmatrix}}_{v} A[31−20]v[−11]=λv[−11]
[3−210][−11]=[−5−1]\begin{bmatrix} 3 & -2 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} -1 \\ 1 \end{bmatrix} = \begin{bmatrix} -5 \\ -1 \end{bmatrix} [31−20][−11]=[−5−1]
计算Au⃗=[42]=2[21]A\vec{u} = \begin{bmatrix} 4 \\ 2 \end{bmatrix} = 2\begin{bmatrix} 2 \\ 1 \end{bmatrix}Au=[42]=2[21],因此u⃗\vec{u}u是特征值2的特征向量;
计算Av⃗=[−5−1]A\vec{v} = \begin{bmatrix} -5 \\ -1 \end{bmatrix}Av=[−5−1],不是v⃗\vec{v}v的倍数,因此v⃗\vec{v}v不是特征向量。
