大数据成矿预测系列(八) | 从定性到概率:逻辑回归——地质统计学派的“集大成者”
前言
这部分应该和证据权重法放在一起,建议先看证据权重法再看这个。
在众多早期的概率性方法中,证据权重法(Weights of Evidence, WofE)是应用最广泛、最被地质学家所接受的方法之一。WofE基于贝叶斯定理的对数线性形式,通过计算权重( 和 )来衡量每一个证据层(如“靠近断层”)与已知矿床点之间的空间关联强度。
然而,WofE方法的有效性建立在一个极其严苛且关键的统计假设之上:所有证据层相对于矿床的发生是“条件独立的”(Conditional Independence, CI)。在地质现实中,这一假设几乎总是被违背的。WofE的权重值提供了这样一种直观的度量,使其易于被非统计学专家所接受。这在地质直觉和统计严谨性之间造成了一种长期的紧张关系。
逻辑回归(Logistic Regression, LR)的出现,正是为了解决WofE模型中“条件独立性”假设这一核心科学难题。

逻辑回归的兴起:针对相关性证据的稳健解决方案
逻辑回归(Logistic Regression, LR)是一种强大的多元统计方法,它被引入成矿预测领域,以克服WofE的主要局限性。 LR 最关键的优势在于:作为一个广义线性模型(GLM),它不需要预测变量(即证据层)之间满足条件独立性的假设。它允许证据层之间存在相关性,这使其在统计上对复杂的地质数据集更加稳健。
从历史背景来看,早在20世纪80年代末至90年代初,地质统计学家(如Agterberg和Bonham-Carter)就开始在同一数据集上并排应用WofE和LR。在这些早期研究中,LR常常被用作一种验证或检查工具,用于评估 WofE 模型中因违反条件独立性假设而可能导致的后果和偏差。
这种从 WofE 到 LR 的过渡,不仅仅是选择了一个“更新”的算法;它是在定量成矿预测领域中一次必要的方法论进展。它解决了由WofE引入的、长期困扰地质学家的核心统计问题(即虚假的CI假设)。学术界普遍认为,逻辑回归是 WofE 方法的“规范泛化”(canonical generalization)。这意味着 WofE 模型实际上是 LR 模型在特定(且通常不成立的)条件下的一个特例。LR 为解决同一科学问题(即多元证据融合预测)提供了一个更通用、更具统计有效性的框架。

科学公式化:逻辑回归作为成矿潜力制图 (MPM) 的工具
定义成矿问题:二元分类
在成矿预测(MPM)中,核心的科学问题可以被精确地表述为:对于一个给定的空间单元(如一个像素或网格单元),综合其所有的地质、地球物理和地球化学观测数据,该单元存在矿床的“概率”是多少?。
这在数学上被构建为一个二元分类问题:
-
因变量 (Y): 是一个二元变量,代表矿床的存在与否(例如, = 存在矿床, = 不存在矿床)9。
-
自变量 (X): 是一个向量,包含了所有在该单元上测量的“证据层”数据(例如,到断层的距离、岩性代码、地球化学异常值、遥感蚀变信息等)。
逻辑回归模型天然地适用于解决此类问题。它本身就是一种为模拟二元事件发生概率而设计的分类算法,这与MPM的目标(预测成矿这一二元事件)完美契合。
数学模型:连接地质变量与对数几率
逻辑回归并不直接对概率 进行建模,因为它要求输出值在0到1之间,而线性方程的输出是 。为了解决这个问题,LR模型对概率 的 logit 变换(即对数几率,log-odds)进行建模。
Logit 变换的定义是:
模型的形式是一个广义线性方程:
其中, 是成矿概率, 是 个地质证据变量, 是截距, 是模型系数。
通过求解 ,我们可以得到最终的概率预测公式,即Sigmoid函数,它呈现为一条“S形”曲线:
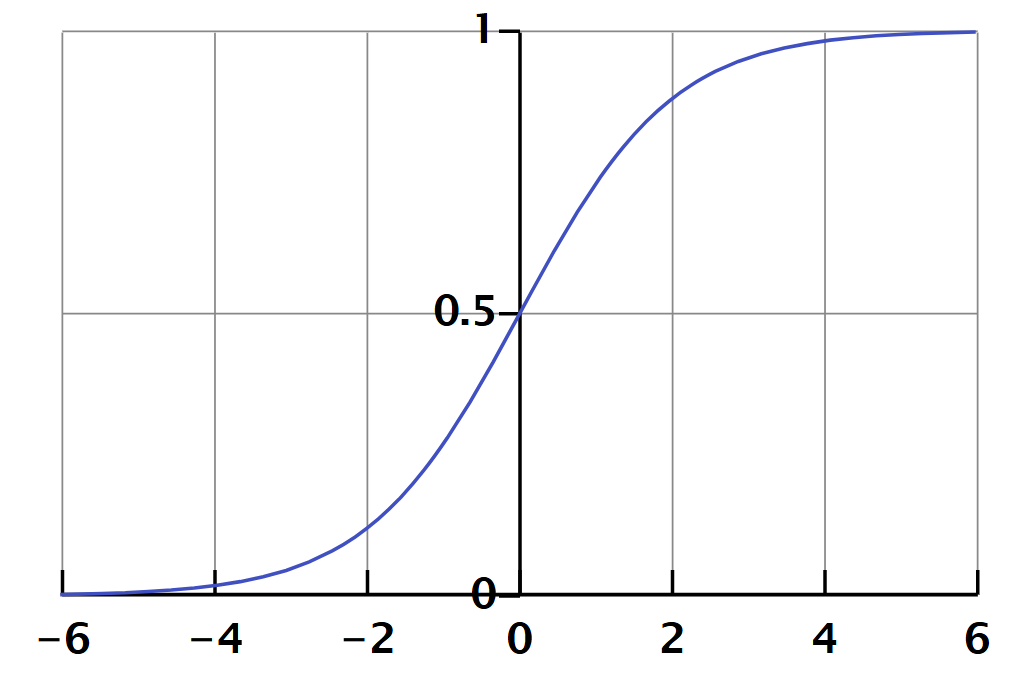
在这个模型中,系数 具有明确的统计意义:它代表了在控制其他所有变量不变的情况下,地质预测变量 每增加一个单位时,成矿“对数几率”(log-odds)的预期变化量。
“大数据”下的工作流:从假设到成图
在现代 MPM 实践中,应用逻辑回归是一个结合了地质专业知识和数据科学的复杂多步骤工作流。
-
矿床系统分析 (MSA) 与数据收集
-
数据准备与特征工程
-
特征选择与优化
-
模型训练与验证
-
生成成矿概率图 (MPM)
详细全文的内容请关注微信公众号:码上地球——数学地球科学查看
此处省略部分内容
结语
我所想要的表格对比终于是在下面完成了。
一个坏消息是这个系列将会很快完结了,好消息是我会在后续出实战教程,手把手教你如何去做(如果我有足够精力的话)。
| 特征 | 信息量法 (IVM) | 证据权法 (WofE) | 逻辑回归 (LR) |
|---|---|---|---|
| 核心假设 | 矿点密度比值可衡量信息量 | 基于贝叶斯定理,权重(W)代表证据强度 | 成矿概率的Logit(对数几率)是预测变量的线性组合 |
| 条件独立性 | 是,隐性假设(简单相加) | 是,方法的关键假设(权重相加) | 否,可以处理相关性强的变量 |
| 透明性 | 高 (白箱) 计算简单直观 | 高 (白箱) 计算和地质意义明确 | 中等 (灰箱) 系数可解释,但模型拟合复杂 |
| 处理非线性 | 能 (间接) 通过数据离散化(分箱) | 能 (间接) 通过数据离散化(分箱) | 能 (显式) 可引入多项式项或进行分箱 |
| 处理因素交互 | 差 传统模型不考虑交互 | 差 传统模型不考虑交互 | 能 (显式) 可在模型中主动添加交互项 |
| 数据需求 | 离散化图层 (二元或多元) 矿点位置 | 离散化图层 (二元或多元) 矿点位置;可处理缺失数据 | 可处理连续和离散变量 矿点和非矿点位置 (Non-deposits) |
| 主要优势 | 1. 极其简单,易于计算和理解 2. 透明度高 | 1. 理论基础坚实 (贝叶斯) 2. 透明度高,地质意义明确 3. 稳健,被广泛验证和接受 | 1. 不要求条件独立性 2. 可处理连续变量 3. 可显式处理因素交互作用 |
| 主要劣势 | 1. 依赖条件独立性假设 2. 传统模型假设因素同等重要 3. 统计上不如WofE稳健 | 1. 严格依赖条件独立性假设 2. 无法处理因素交互 3. 需将连续数据二元化,损失信息 | 1. 需要非矿点样本 2. 透明性稍差 3. 易受“共线性”问题干扰 |

科学探索永无止境,本文仅为笔者个人学习总结。因知识所限,文中若有不当之处,敬请方家斧正。
参考内容
-
Zhang, D., Ren, N., & Hou, X. (2018). An improved logistic regression model based on a spatially weighted technique (ILRBSWT v1. 0) and its application to mineral prospectivity mapping. Geoscientific Model Development, 11(6), 2525-2539.
-
Kost, S., Rheinbach, O., & Schaeben, H. (2021). Using logistic regression model selection towards interpretable machine learning in mineral prospectivity modeling. Geochemistry, 81(4), 125826.
-
Fu, Z., Zheng, X., Yan, Y., Xu, X., Zhou, F., Li, X., ... & Mai, W. (2025). The Evolution of Machine Learning in Large-Scale Mineral Prospectivity Prediction: A Decade of Innovation (2016–2025). Minerals.
-
Xiong, Y., & Zuo, R. (2018). GIS-based rare events logistic regression for mineral prospectivity mapping. Computers & Geosciences, 111, 18-25.
