easy_RSA(攻防世界)
写在前面:

原题:传送门
题目如下:
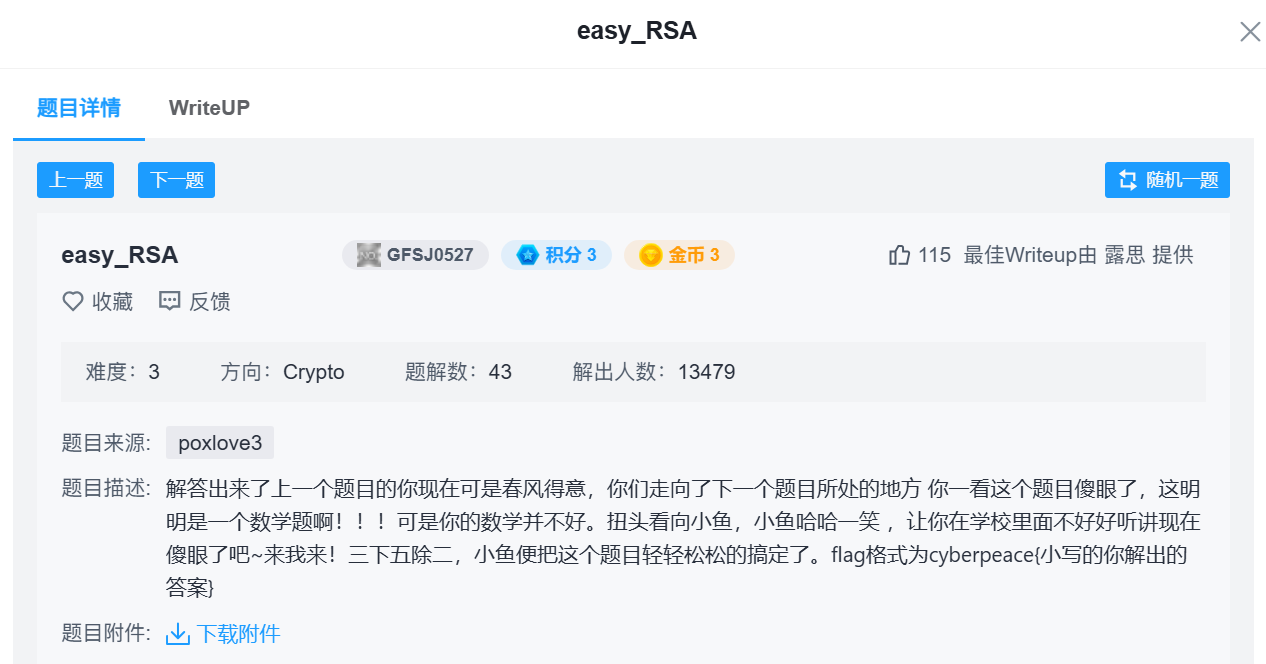
附件打开
是一个文本文件:
在一次RSA密钥对生成中,假设p=473398607161,q=4511491,e=17
求解出d
我们首先要知道什么事 RSA
在软件开发和网络安全领域,RSA公私钥的生成是实现非对称加密的重要步骤。RSA算法依赖于一对密钥,即公钥和私钥,用于加密和解密数据,以及进行数字签名和验证。公钥可以公开分享,而私钥必须保密。
求解RSA私钥d
已知RSA公钥生成参数:
p = 3487583947589437589237958723892346254777
q = 8767867843568934765983476584376578389
e = 65537
我们需要计算私钥 d,其公式为: d ≡ e⁻¹ (mod φ(n)),其中 φ(n) = (p-1) * (q-1)。
以下是Python代码实现:
import gmpy2
# 已知参数
p = 3487583947589437589237958723892346254777
q = 8767867843568934765983476584376578389
e = 65537
# 计算 φ(n)
phi = (p - 1) * (q - 1)
# 计算 d
d = gmpy2.invert(e, phi)
# 输出结果
print(f"flag{{{d}}}")
运行结果验证
将上述代码运行后,程序会输出私钥 d 的值,并按照题目要求的格式返回结果,例如: flag{d}
有童鞋可能要问了:“ d = gmpy2.invert(e, phi) ” 是什么东东?
d = gmpy2.invert(e, phi):
gmpy2.invert(e, phi) 函数是 gmpy2 库中的一个方法,用于计算模逆元。具体来说,它尝试找到一个整数 d 使得:
(e×d)≡1 (mod ϕ)(e×d)≡1 (mod ϕ)
为了成功计算 d,以下条件必须满足:
1、e 和 phi 必须互质(即最大公约数为 1)。如果 e 和 phi 不互质,则不存在这样的 d 满足上述同余方程,此时 gmpy2.invert 将返回 0,表示找不到模逆。
2、e 必须小于 phi。
注意事项
要用 gmpy2库中的invert函数需要确保安装了 gmpy2 库,可通过 pip install gmpy2 安装。
如下图:
像我这样就是下载好了
好了 有了求d的公式和数据了 我们就可以打开我们心爱的 pycharm 了
公式一代数据一改得到:
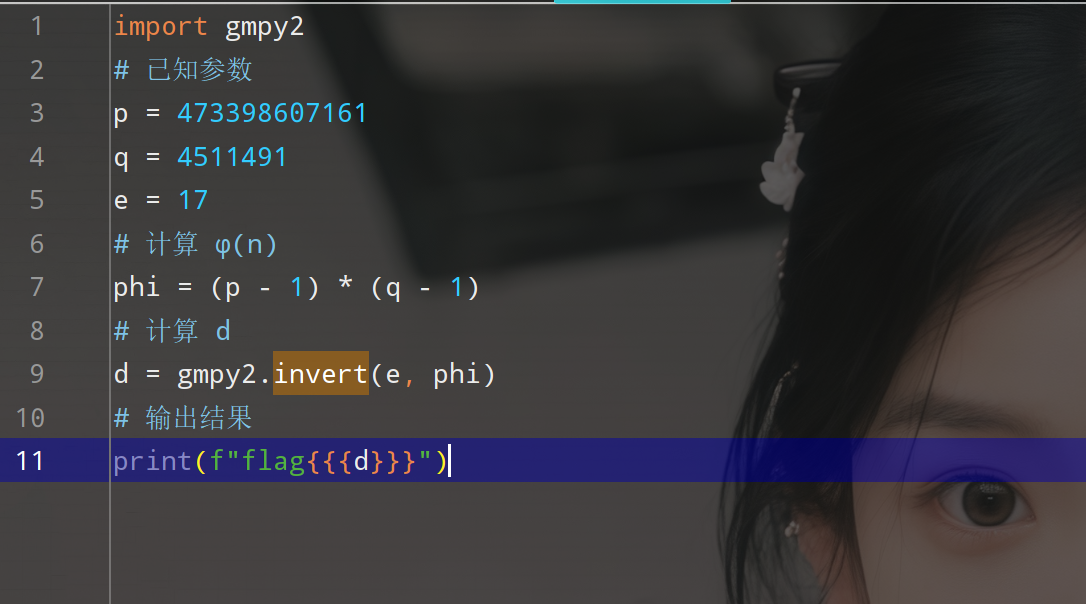
输出:
flag{125631357777427553}
所以结合题目意思 答案应该是
cyberpeace{125631357777427553}
整理不易,头发掉了几根。觉得有收获的话,点个赞关注一下呗? 我保证,我的主页里还有更多让你头发比你掉得还多的好东西!

写在后面: