代码随想录 Q79.全排列

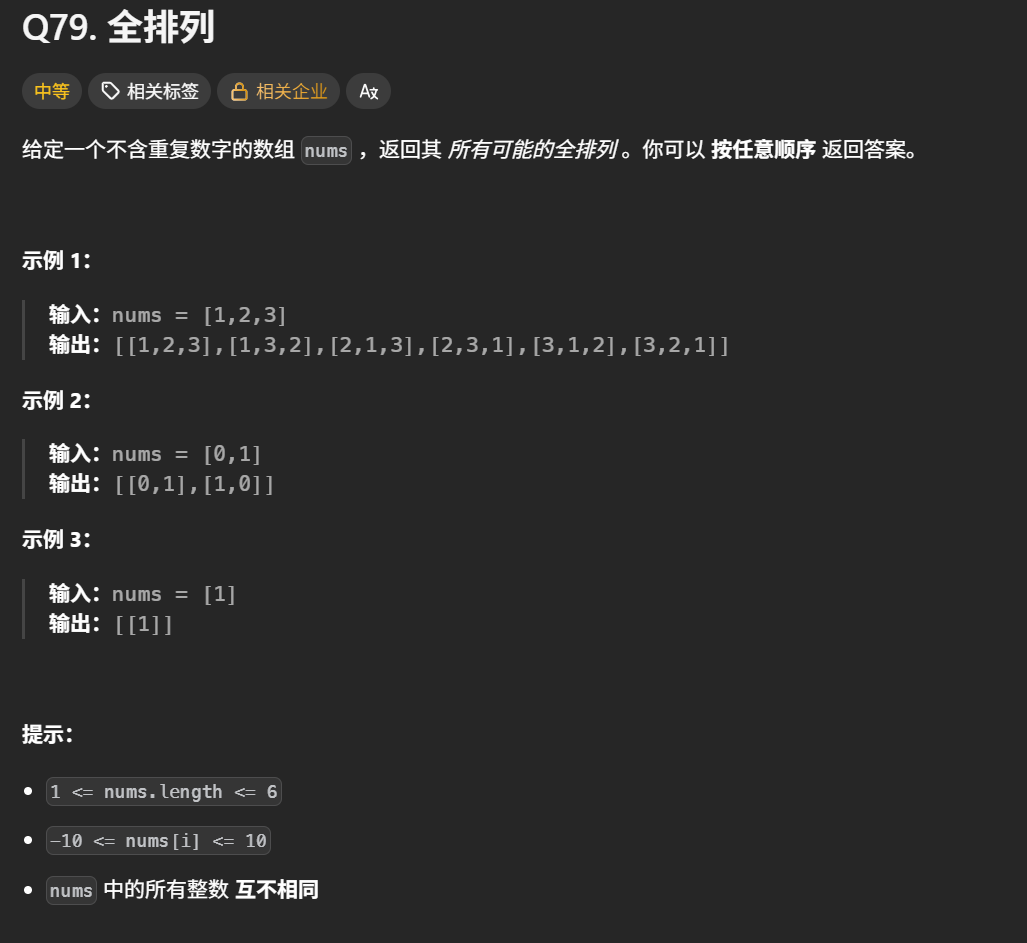
题目要求：排列问题，区别于前面的组合问题、分割回文串和子集问题。以[1,2,3]为例，抽象成树形结构如下所示：

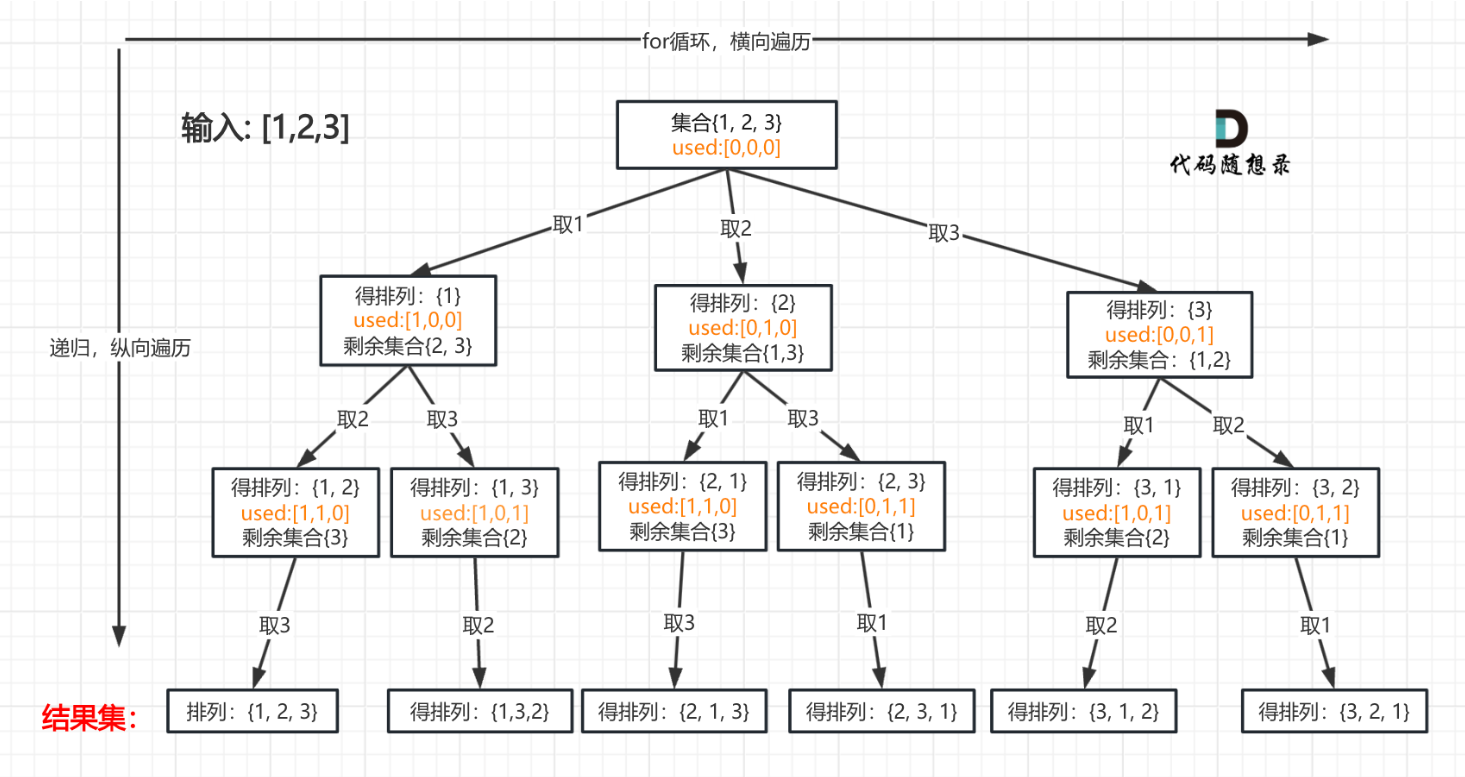
回溯三部曲：

1.递归函数的参数：由于排列是有序的，也就是说[1,2]和[2,1]是两个集合，这和之前分析的子集以及组合不同。因此处理排列问题不需要startIndex,但是排列问题需要一个used数组来标记已经选择的元素，如下图橘黄色部分所示：

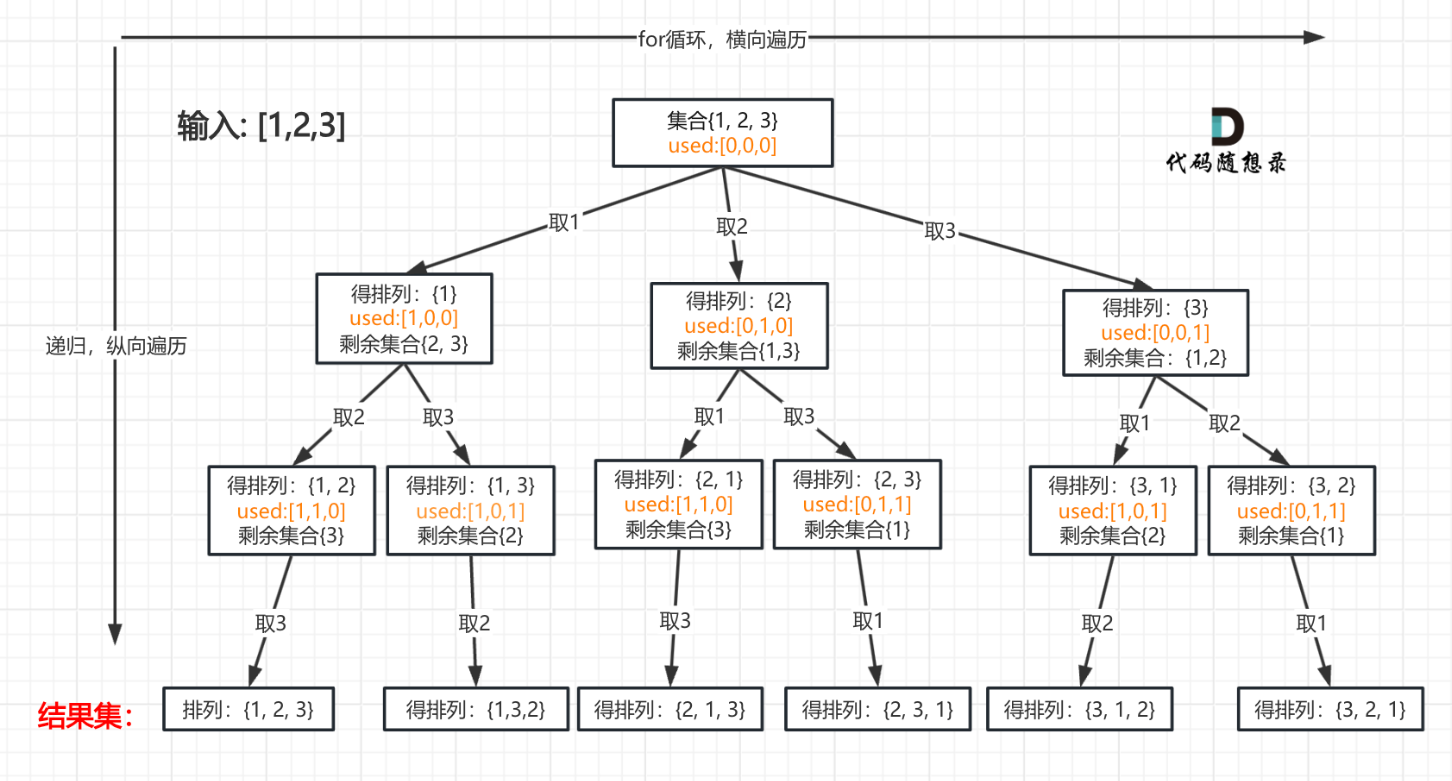
    List<List<Integer>> res = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();boolean[] used;

private void backTracking(int[] nums)

2.递归终止条件：如下图所示，叶子节点是收集结果的地方，所以到达叶子节点时终止。到达叶子节点的条件是收集元素的path数组的大小达到nums数组时，说明找到了一个全排列，也表示到达了叶子节点。

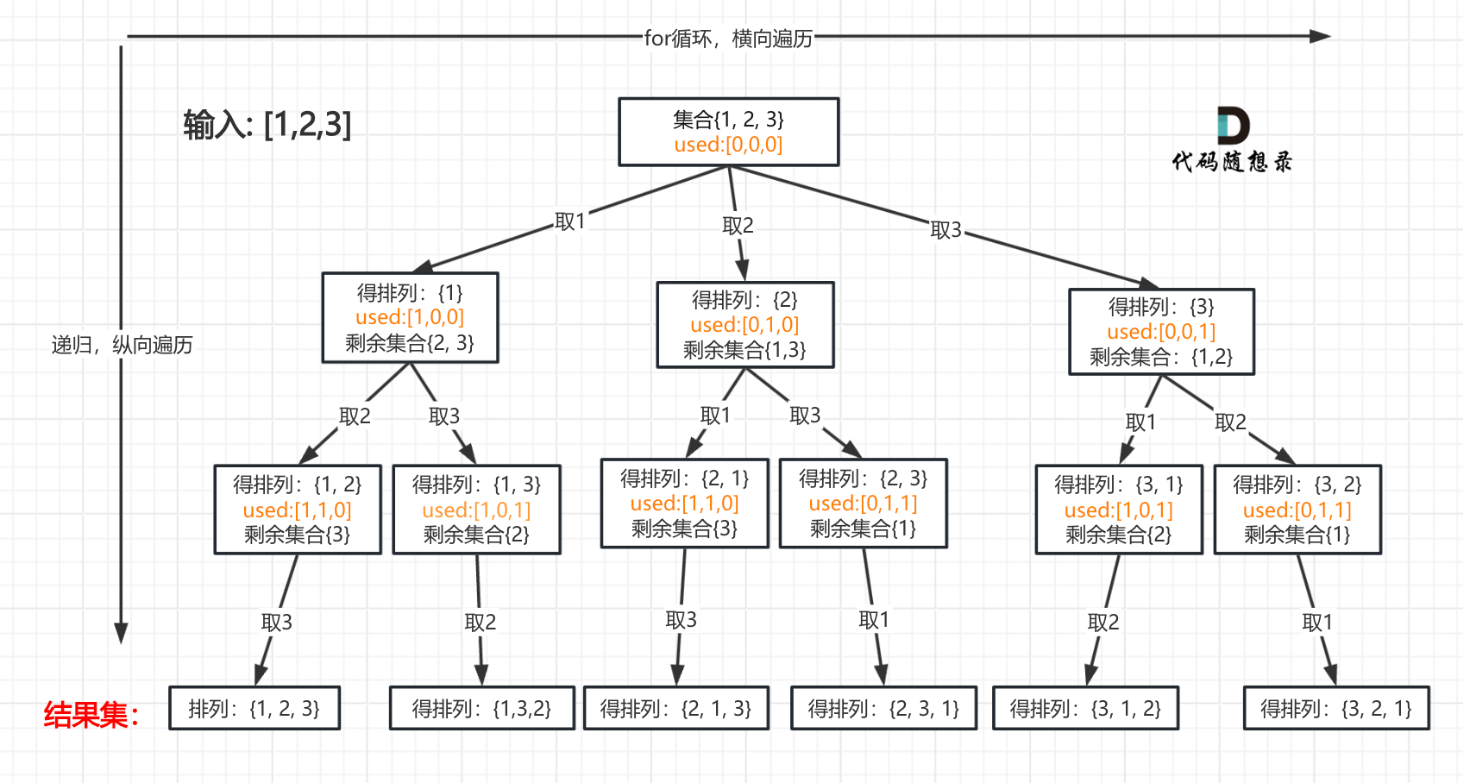
        if(path.size() == nums.length){res.add(new ArrayList<>(path));return;}

3.确定单层搜索的逻辑：

（1）排列问题最大的不同在于不需要使用startIndex。因为排列问题每次都要从头开始搜索，例如元素1在[1,2]中已经使用过了，但是在[2,1]中还要再使用一次1。

（2）used数组其实就是记录path里有哪些元素使用了，一个排列里一个元素只能使用一次。

代码如下所示：

        for(int i = 0;i < nums.length;i++){if(used[i]){continue;}used[i] = true;path.add(nums[i]);backTracking(nums);path.removeLast();used[i] = false;}

附代码：

class Solution {List<List<Integer>> res = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();boolean[] used;public List<List<Integer>> permute(int[] nums) {if(nums.length == 0){return res;}used = new boolean[nums.length];backTracking(nums);return res;}private void backTracking(int[] nums){if(path.size() == nums.length){res.add(new ArrayList<>(path));return;}for(int i = 0;i < nums.length;i++){if(used[i]){continue;}used[i] = true;path.add(nums[i]);backTracking(nums);path.removeLast();used[i] = false;}}
}