强化学习RL

概述

Reinforcement Learning，RL，机器学习的一个子领域，通过与环境的交互来学习如何实现特定的目标。

在RL中，智能体(Agent)在环境中通过执行动作(Action)来改变状态(State)，并根据状态转移获得奖励(Reward)，目标是最大化其长期累积奖励，通常涉及到策略(Policy)的学习，即在给定状态下选择最佳动作的规则。核心机制包括试错和反馈，通过价值函数(Value Function)或Q函数形式化描述最优决策过程。

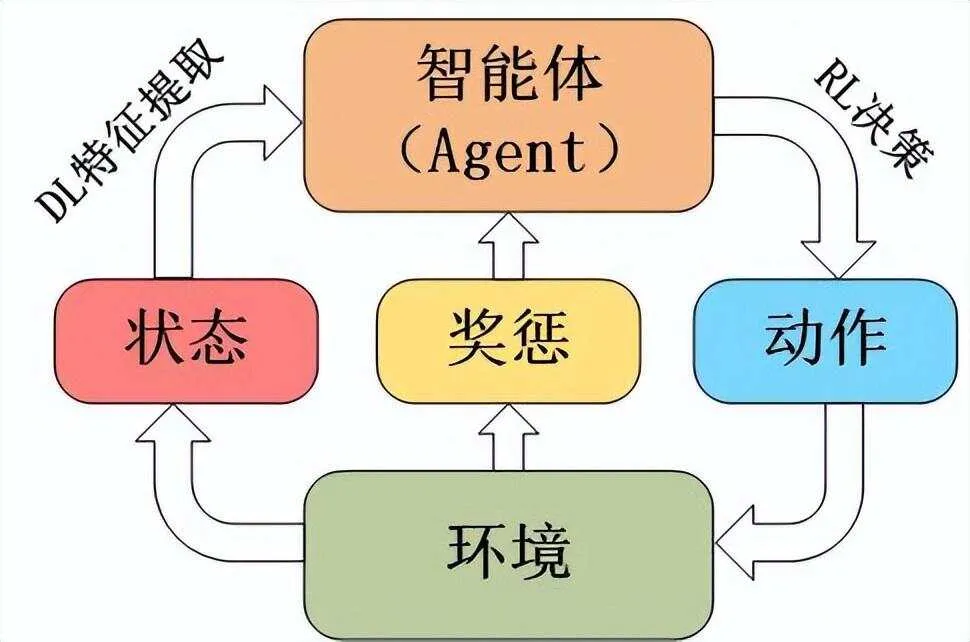
组件：

• 状态：智能体所处的环境情况；
• 动作：智能体在特定状态下可以执行的行为；
• 奖励：智能体执行动作后从环境中获得的反馈，用于评价动作的好坏；
• 策略：智能体选择动作的规则或策略，可以是确定性的或随机性的；
• 价值函数：预测智能体从某个状态出发，遵循特定策略所能获得的累积奖励。

Q值函数，也称为动作价值，动作价值函数(Action-Value Function)，一种特殊的价值函数，估计在给定状态下采取特定动作的预期回报。

三个模型

• 策略模型：指AI在不同环境状态下应该采取的行动，或采取各个行动的概率分布。
• 价值模型：用于评估AI在某个状态下的价值，表示AI从某个状态开始，遵循某种策略所能获得的长期累积奖励的估计值。
• 奖励模型：用于量化AI在环境中执行某个动作时所获得奖励的函数，就是告诉AI什么样的行为可获得更高奖励，什么样的行为会得到惩罚。

通常建模为马尔可夫决策过程（Markov decision process，MDP），包含状态、动作、状态转移概率、奖励和折扣因子五个关键要素，用于描述智能体与环境之间的交互和决策优化。

分类

基于模型和无模型（是否依赖环境模型）、基于价值和基于策略（学习价值函数或直接策略）、在线和离线策略（数据来源）、交叉熵方法（鼓励探索）以及赌博机和梯度赌博机方法（无状态决策和梯度优化）。

优势函数（A）是动作值函数（Q）与状态值函数（V）的差值，即$A=Q-V$。

• V：衡量状态的整体价值
• Q：衡量状态-动作组合的价值
• A：则评估特定动作相对于平均策略的增益

值函数估计的三种主要方法：

• MC：蒙特卡洛，通过完整轨迹估计，无偏但高方差，适合奖励密集且随机性小的场景；优点：无需模型假设，直接基于实际回报学习，长期无偏且期望准确。缺点：方差较大，仅依赖回合最终回报导致估计波动大，奖励稀疏或变化频繁时方差进一步增大。
• TD：时间差分，利用部分轨迹信息，低方差但高偏差，适合快速更新和实时场景；优点：方差小，适合在线学习，可实时更新。缺点：偏差较大，依赖估计值更新，易受初始偏差影响。
• GAE：广义优势估计，结合两者优点。通过参数$\lambda$灵活权衡偏差与方差，利用加权平均的TD误差估计优势函数，减少偏差并控制方差。适用于需要平衡两者的通用场景。缺点：相比纯TD或MC方法，计算量更大，需在每一步计算加权TD误差。

根据是否在线，分类：

• On-policy：在线策略，通过与环境实时交互获取数据并更新模型。使用与学习策略相同的行为策略采样数据。数据分布与策略一致，收敛性更可靠但样本效率低；代表算法：PPO和A2C/A3C
• Off-policy：离线策略，依赖预先收集的静态数据集进行训练，不与环境交互。允许行为策略与目标策略不同，支持利用历史数据（如经验回放）进行学习。可重用数据、样本效率高，但存在分布偏移和收敛困难的问题。代表算法：Q-Learning、DQN、SAC和TD3。

MC

Monte Carlo，蒙特卡洛，为强化学习提供一种概念上简单易懂的方式：完整地经历一个个情节，观察总回报，并据此更新价值估计。核心观点是，如果运行足够多的情节，平均回报将会收敛到它们的期望值。

核心步骤：

1. 策略评估：任意初始化价值估计；
2. 生成情节：遵循当前策略生成完整的情节；
3. 计算回报：对于访问过的每个状态，计算该次访问后的回报（奖励总和）；
4. 更新价值估计：通过平均回报来更新价值函数；
5. 策略改进：根据更新后的价值函数，使策略变为贪婪策略；
6. 重复：持续上述步骤，直到收敛。

独特之处在于，它们会等到一个情节结束后才进行任何更新。这使得它们能够观察到实际回报，而不是基于当前的价值近似来进行估计。

主要有两种类型：

• 首次访问：仅根据一个情节中首次访问某个状态时的情况来更新价值估计。
• 每次访问：根据情节中每次访问某个状态的情况来更新价值估计。

例如，如果状态$s$在一个情节中出现三次，首次访问蒙特卡洛方法只会使用第一次出现后的回报来更新$V(s)$，而每次访问蒙特卡洛方法会使用这三次的全部回报。

关键挑战，要确保所有的状态-动作对都被充分访问，以便进行准确的价值估计。有两种常见的方法可以解决这个问题：

• 探索起始：从随机选择的状态-动作对开始情节；
• ε-贪婪策略：以概率$\epsilon$选择随机动作，而不是贪婪动作。

在大多数情况下，后一种方法更具实用性，因为它不需要能够随意设置起始状态和动作。

TD

Temporal Difference，时间差分。MC要等到情节结束才更新价值估计，TD则基于其他估计来更新价值，这个过程被称为引导（bootstrapping），因此是一种结合蒙特卡洛方法和动态规划元素的混合方法。

核心：根据当前的估计立即进行更新。

时间差分更新遵循以下模式：$$V(S_t)\leftarrow V(S_t)+\alpha \left[R_{t+1}+\gamma V(S_{t+1})-V(S_t)\right]$$
方括号中的项就是时间差分误差，即当前估计与新的目标估计之间的差值。

对比

特性	MC	TD
回合完整性要求	需要完整回合	可以从不完整回合中学习
更新时机	回合结束时更新	每一步后更新
方差	方差较高	方差较低
偏差	无偏估计	对初始估计有偏差
初始值敏感性	较不敏感	较为敏感
计算效率	效率较低	效率较高
处理连续任务的能力	具有挑战性	天然适用

根本区别在于它们估计回报的方式：

• MC使用采样：对完整情节的实际回报求平均
• TD使用引导：基于其他估计来更新估计值

分类：

• 在线：SARSA
• 离线：Q-Learning

SARSA

State-Action-Reward-State-Action，状态-动作-奖励-状态-动作，，反映其更新规则中使用的事件序列。一种在线策略方法，意味着它学习的是实际遵循的策略的价值。

关键：SARSA在学习过程中考虑实际行为。

Q-Learning

通过迭代更新Q值来逼近最优Q函数。算法流程：

• 初始化Q表：创建一个Q表，通常初始化为零或其他小的随机值，以表示对环境的无知。Q表将随着智能体与环境的交互而不断更新；Q表是一个二维数组，行表示状态，列表示动作。每个单元格$Q(s,a)$表示在状态$s$下采取动作$a$的预期回报。
• 选择动作：在每个时间步骤中，智能体根据当前状态和Q表选择一个动作。通常涉及到探索和利用的权衡，以确保在学习过程中不断探索新的动作策略。使用ε-greedy策略来平衡探索(exploration)和利用(exploitation)：以$1-\epsilon$的概率选择当前Q值最高的动作，以$\epsilon$的概率随机选择一个动作；允许智能体在大多数时间利用已知的最佳动作，同时保留一定概率去探索新的动作，以发现可能更好的策略。
• 执行动作：智能体执行所选择的动作，并观察环境的响应，包括获得的奖励信号和新的状态；
• 更新Q值：根据观察到的奖励信号$r$和新状态$s^{\prime }$，智能体更新Q值。涉及到使用Q-Learning的更新规则，如贝尔曼方程；Q-Learning的核心是更新Q值的公式，该公式基于贝尔曼方程：$$Q(s,a)\leftarrow Q(s,a)+\alpha \left[r+\gamma ma{x}_{a^{\prime }}Q(s^{\prime },a^{\prime })-Q(s,a)\right]$$其中：
  • $Q(s,a)$是在状态$s$下采取动作$a$的$Q$值；
  • $\alpha$是学习率，控制新信息的影响程度，即控制新估计值与旧估计值之间的权衡；
  • $r$是在执行动作$a$后获得的即时奖励；
  • $\gamma$是折扣因子，表示未来奖励的重要性；
  • $s^{\prime }$是执行动作$a$后观察到的新状态；
  • $a^{\prime }$是在新状态$s^{\prime }$下选择的下一个动作；
  • $ma{x}_{a^{\prime }}Q(s^{\prime },a^{\prime })$是在新状态$s^{\prime }$下所有可能动作的最大Q值，表示对未来奖励的最大预期。
• 重复迭代：智能体不断地执行上述步骤，与环境互动，学习和改进Q值函数，直到达到停止条件（最大迭代次数或Q值收敛）。

注：贝尔曼方程是动态规划中的核心原理，描述一个状态的价值可通过即时奖励和未来价值的总和来计算。

Q学习在假设完美执行的情况下找到真正的最优路径，而SARSA找到的是考虑了当前探索策略的最优路径。

通过这些步骤，Q-Learning能够学习在给定状态下采取哪些动作能够最大化长期累积奖励，而无需了解环境的具体动态。这种无模型的方法使得Q-Learning在许多实际应用中非常有用，尤其是在模型难以获得或过于复杂时。

在一定条件下，Q-Learning能够收敛到最优策略：

• 有限状态和动作空间：状态空间和动作空间必须是有限集，保证Q表能够被完全更新；
• 探索策略：智能体必须对所有状态-动作对进行无限次的探索，以确保Q值能够被准确估计；
• 学习率衰减：$\alpha$需要随时间衰减，以保证Q值更新的稳定性；
• 折扣因子$\gamma$：必须满足$0<\gamma <1$，以平衡即时奖励和未来奖励的重要性

在实际应用中，Q-Learning的收敛性可通过以下方式进行分析：

• 迭代次数：随着迭代次数的增加，Q值会逐渐稳定，算法趋于收敛；
• 奖励信号：奖励信号的一致性和可靠性对Q值的收敛性有重要影响；
• 探索策略：ε-greedy策略中的$\epsilon$值对收敛速度和稳定性有显著影响。

Q-Learning中的探索与利用平衡是通过ε-greedy策略实现的，允许智能体在探索新动作和利用已知最佳动作之间进行权衡：

• 探索：以$\epsilon$的概率随机选择动作，以发现新的状态-动作对和潜在的更高回报；
• 利用：以的概率选择当前Q表中Q值最高的动作，以利用已有的知识。

$\epsilon$值的动态调整对平衡探索与利用至关重要：

• 初始值：初始时，$\epsilon$值通常设置较高，以促进探索；
• 衰减：随着学习进行，$\epsilon$值逐渐减小，使智能体更多地利用已知的最佳策略；
• 自适应调整：在某些变体中，$\epsilon$值可根据学习进度自适应调整，以优化探索与利用的平衡。

应用场景：游戏（棋盘类，如Atari、围棋）、机器人导航和自动驾驶（路径规划、自主决策）、资源管理（优化资源分配，如网络流量控制和电力分配）、推荐系统、NLP（如对话系统和机器翻译）、健康医疗（可用于制定辅助诊断、治疗计划，以及医疗资源的优化配置）、智能教学系统。

AC

Actor-Critic，策略-价值模型

TODO

DSAC-T

论文，Distributional Soft Actor-Critic with Three Refinements，论文作者开源DSAC-v1，

面向相对较小的模型（如1B以下），并用于自动驾驶、机器人、游戏等任务，采用AC架构，通过价值函数模型为策略改进提供依据。

使用状态-动作价值函数$Q(s,a)$，代表在状态下采取动作后未来回报的期望值。并且DSAC-T进一步将其扩展为了分布式值函数$Z(s,a)$，输出价值估计的均值和方差，通过对值分布的建模，有效缓解过估计问题。在基准测试环境中，DSAC-T算法以50%以上的优势领先于OpenAI的PPO和Deepmind的DDPG等算法。

PRIME

TODO

DPO

论文，Direct Preference Optimization，直接偏好优化，离线优化，直接利用偏好数据训练策略，无需显式奖励模型，训练更简单，但易受分布偏移影响，稳定性较差。直接微调策略模型，依赖偏好数据中的对比样本（选择vs拒绝）。在奖励函数中直接加入KL散度（Kullback-Leibler Divergence）惩罚项，以防止策略更新幅度过大。
$${\mathcal{L}}_{\mathrm{DPO}}({\pi }_{\theta };{\pi }_{\mathrm{ref}})=-{\mathbb{E}}_{(x,y_w,y_l)\sim D}\left[\log \sigma \left(\beta \log \frac{{\pi }_{\theta }(y_w\mid x)}{{\pi }_{\theta }(y_l\mid x)}-\beta \log \frac{{\pi }_{\theta }(y_l\mid x)}{{\pi }_{\mathrm{ref}}(y_l\mid x)}\right)\right]$$

优点：

• 简化流程：直接利用偏好数据，省去奖励模型训练，计算成本更低；
• 适合离线场景：在语言模型对齐等任务中表现优异。

缺点：

• 分布偏移敏感：策略可能偏离偏好数据分布，导致性能下降；
• KL约束弱化：偏好确定性增强时，KL正则化效果减弱，易过拟合。

PPO

论文，Proximal Policy Optimization，近端策略优化，依赖价值模型来估计优势函数（Advantage），即通过额外训练一个神经网络来预测长期收益的基线值。基于令牌级（Token-Level）的奖励计算，直接评估每个生成标记的收益。通过剪辑目标函数和信任区域约束策略更新，稳定性较高。
$$J_{\mathrm{PPO}}(\theta )={\mathbb{E}}_{q\sim p(Q),o\sim {\pi }_{{\theta }_{\mathrm{old}}}(O\mid q)}\left[\frac{1}{|o|}\sum _{t=1}^{|o|}\min \left(\frac{{\pi }_{\theta }(o_t|q,o_{<t})}{{\pi }_{{\theta }_{\mathrm{old}}}(o_t|q,o_{<t})}{A}_t,\mathrm{clip}\left(\frac{{\pi }_{\theta }(o_t|q,o_{<t})}{{\pi }_{{\theta }_{\mathrm{old}}}(o_t|q,o_{<t})},1-ϵ,1+ϵ\right)A_t\right)\right]$$

优点：

• 稳定性强：通过剪辑目标函数（概率比）限制策略更新幅度，避免训练崩溃；
• 通用性高：适用于连续/离散动作空间，广泛用于机器人等领域。

缺点：

• 计算开销大：需频繁环境交互和奖励模型调用，样本效率较低；需要维护一个与策略模型大小相当的价值网络，导致显著的内存占用和计算代价。
• 策略更新不稳定：策略更新依赖于单个动作奖励值，可能导致较高方差，影响训练稳定性；
• 依赖奖励模型质量：若奖励模型设计不佳，策略可能过优化。

GRPO

DeepSeek提出，GRPO论文，DeepSeek-R1论文，Group Relative Policy Optimization，组相对策略优化。

主流RL通过引入价值模型，可更准确地判断每个动作的优劣，从而改进策略。价值函数估计的准确性直接决定策略好坏。在大多数任务中，能给出较合理的过程奖励设定，此时价值函数可快速收敛。而对于部分只具有结果奖励的任务，例如围棋，则可以通过大量的样本采集和模型更新，获得一个较准确的价值模型。因此在这些任务上使用RL时，引入价值模型可以大幅提升算法性能表现。但对于LLM，不仅过程奖励难以合理定义，其巨大的参数规模使得大量采样更新不可行。因此GRPO放弃使用价值函数模型，直接优化策略。

移除价值模型，改用群体归一化奖励作为基线。不需要使用价值模型，采用群体相对奖励机制，用当前策略对同一问题多次生成回答，并以这些回答的平均奖励估计基线，计算相对奖励和优势。这减少训练资源消耗，并避免价值估计不准的问题。

将KL散度作为正则化项直接引入损失函数中，从而更直接地控制策略更新的稳定性。但可能因组计算引入复杂性而影响稳定性。相比PPO，内存占用减少约40%，训练速度更快。

GRPO的优势函数计算有两个版本，分别对应结果监督和过程监督两种奖励方式，结果监督只在每个回答结束时提供奖励，而过程监督在每个推理步骤结束时提供奖励。DeepSeek-R1-Zero训练采用的是结果监督

J G R P O ( θ ) = E q ∼ P ( Q ) , { o i } i = 1 G ∼ π θ o l d ( O ∣ q ) [ 1 G ∑ i = 1 G 1 ∣ o i ∣ ∑ t = 1 ∣ o i ∣ ( min ⁡ [ π θ ( o i , t ∣ q , o i , < t ) π θ o l d ( o i , t ∣ q , o i , < t ) A ^ i , t , c l i p ( π θ ( o i , t ∣ q , o i , < t ) π θ o l d ( o i , t ∣ q , o i , < t ) , 1 − ϵ , 1 + ϵ ) A ^ i , t ] − β D K L ( π θ ∥ π r e f ) ) ] \mathcal{J}_{\mathrm{GRPO}}(\theta)=\mathbb{E}_{q\sim P(Q),\,\{o_i\}_{i=1}^G\sim \pi_{\theta_{\mathrm{old}}}(O|q)}\left[\frac{1}{G}\sum_{i=1}^{G}\frac{1}{|o_i|}\sum_{t=1}^{|o_i|}\left(\min\left[\frac{\pi_\theta(o_{i,t}|q,o_{i,<t})}{\pi_{\theta_{\mathrm{old}}}(o_{i,t}|q,o_{i,<t})}\hat{A}_{i,t},\,\mathrm{clip}\left(\frac{\pi_\theta(o_{i,t}|q,o_{i,<t})}{\pi_{\theta_{\mathrm{old}}}(o_{i,t}|q,o_{i,<t})},1-\epsilon,1+\epsilon\right)\hat{A}_{i,t} \right] - \beta \mathcal{D}_{\mathrm{KL}} \left( \pi_\theta \| \pi_{\mathrm{ref}} \right) \right) \right] JGRPO​(θ)=Eq∼P(Q),{oi​}i=1G​∼πθold​​(O∣q)​ ​G1​i=1∑G​∣oi​∣1​t=1∑∣oi​∣​(min[πθold​​(oi,t​∣q,oi,<t​)πθ​(oi,t​∣q,oi,<t​)​A^i,t​,clip(πθold​​(oi,t​∣q,oi,<t​)πθ​(oi,t​∣q,oi,<t​)​,1−ϵ,1+ϵ)A^i,t​]−βDKL​(πθ​∥πref​)) ​
解读：
$$Ratio=\frac{{\pi }_{\theta }(o_{i,t}|q,o_{i,<t})}{{\pi }_{{\theta }_{\mathrm{old}}}(o_{i,t}|q,o_{i,<t})}$$
是当前策略与旧策略的概率比，${\hat{A}}_{i,t}$是分组相对奖励，通过对每个动作的奖励进行归一化得到。

对比PPO

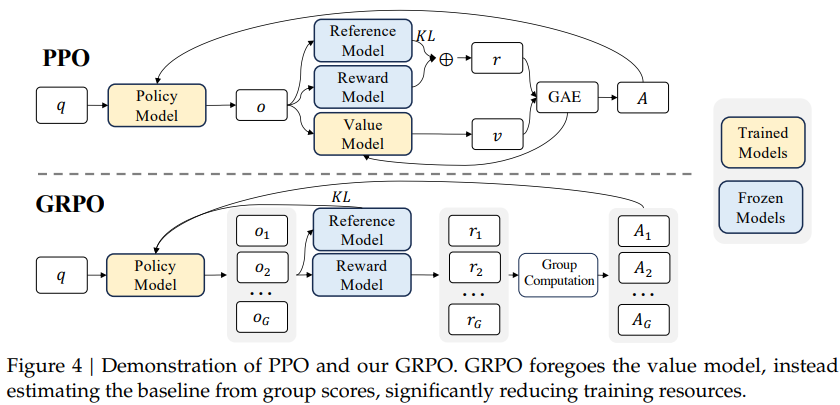
实现流程：

1. 环境定义：定义群体中各个智能体，每个智能体都有自己的状态空间、策略空间和奖励函数，环境也会根据智能体的动作给出反馈
2. 分配初始策略：为每个智能体分配一个初始策略
3. 群体交互与数据收集：让每个智能体和环境交互，并根据自己的策略选择动作，然后更新环境状态
4. 相对关系分析：分析智能体之间的相对关系，比如哪些智能体协作更紧密，哪些智能体的动作对环境影响更大
5. 策略优化：根据相对关系分析的结果，使用梯度下降算法更新策略网络的参数，使得群体目标实现概率最大化
6. 重复迭代：重复步骤3~5，直到满足一定的终止条件。

算法流程：

• 采样动作组：对于每个输入状态$s$，从当前策略${\prod }_{\theta }$中采样一组动作 { a 1 , a 2 , . . . , a G } \{a_1,a_2,...,a_G\} {a1​,a2​,...,aG​}，采样基于策略模型的概率分布，确保多样性。
• 奖励评估：每个采样动作$a_i$都会通过奖励函数$R_{ai}$进行评估，得到对应的奖励值$r_i$。奖励函数可根据具体任务设计，在数学推理任务中，奖励函数可基于答案的正确性。
• 计算相对优势：将每个动作的奖励值进行归一化处理，得到相对优势${\hat{A}}_i$，可通过公式计算：${\hat{A}}_i=\frac{r_i-mean(\mathbf{r})}{std(\mathbf{r})}$
• 策略更新：根据计算得到的相对优势${\hat{A}}_i$，更新策略模型的参数$\theta$。目标是增加具有正相对优势的动作的概率，同时减少具有负相对优势的动作的概率。
• KL散度约束：为了防止策略更新过于剧烈，GRPO在更新过程中引入KL散度约束。通过限制新旧策略之间的KL散度，确保策略分布的变化在可控范围内。

优点：

• 多源信息整合：通过组计算模块处理多观测值，提升决策质量；
• 继承PPO优势：保留剪辑目标函数和稳定更新机制；
• 计算效率：通过避免价值网络的使用，显著降低计算和存储需求，提高训练效率；
• 稳定性：通过组内相对奖励的计算，减少策略更新的方差，确保更稳定的学习过程；
• 可控性：引入KL散度约束，能够更精细地控制策略更新的幅度，保持策略分布稳定性。

缺点：

• 复杂度高：组计算模块增加模型参量和训练难度；
• 采样成本：需要对每个状态采样一组动作，可能增加采样成本；
• 应用场景有限：目前主要见于特定扩展任务，通用性验证不足，尤其是在奖励信号稀疏的情况下。

对比RLHF

维度	GRPO	OpenAI RLHF
算法原理	通过组内相对奖励机制估计优势函数，无需价值网络，直接在损失函数中加入KL散度正则项	基于人类反馈，通过奖励建模和强化学习优化模型输出，使其符合人类偏好
训练效率	简化训练流程，降低计算开销和内存需求，训练效率高，收敛速度快	训练过程复杂，包括监督学习、奖励模型训练和强化学习优化，计算成本高
策略更新稳定性	策略更新稳定，通过组内相对奖励减少方差，直接的KL散度正则化确保更新可控	策略更新稳定性依赖于奖励模型的准确性和标注数据质量，可能存在偏差
应用场景	特别适用于需要推理能力的任务，如数学推理、代码生成等	通用性强，适用于各种需要优化模型输出以符合人类偏好的任务，如聊天机器人等
资源需求	资源需求低，高效且具有成本效益，适合大规模语言模型	资源需求高，计算成本高昂，需要大量人类标注数据和计算资源
模型性能	在特定任务上性能优异，如数学推理任务解题准确率显著提升	在通用应用中性能出色，生成的输出更符合人类偏好，减少有害内容生成
优缺点	优点：无需价值网络，降低计算开销；策略更新稳定，适合复杂任务；针对特定任务优化，生成质量高。 缺点：采样成本高，推理时间增加；奖励模型设计复杂；策略更新可能过于保守	优点：优化人类偏好，提升用户体验；通用性强，适用范围广；确保高质量输出。 缺点：训练成本高，标注数据需求大；标注偏差影响性能；训练稳定性问题

对比

均属于策略优化方法相同：通过调整策略参数（如神经网络权重）来最大化累积奖励或偏好数据匹配度。

都是通过熵正则化或其他机制（如KL散度约束）鼓励策略探索，避免过早收敛到次优解。

DPO和PPO梯度更新方式相同：均采用梯度下降法优化目标函数，例如PPO的替代目标函数、DPO的偏好对数损失函数。

PPO和GRPO架构相同：均包含策略模型与价值模型，涉及奖励或偏好建模。

总结：

• DPO：在离线偏好对齐任务中更高效，但需解决分布偏移和稳定性问题；
• PPO：通用性强、稳定性高的在线RL基准方法，但依赖奖励模型和大量交互数据；
• GRPO：作为PPO扩展，在复杂多观测任务中潜力大，但需进一步验证其普适性。

OREO

论文，Offline Reasoning Optimization，离线推理优化，通过优化软贝尔曼方程，联合训练策略模型和价值函数，克服现有方法在处理稀疏奖励和信用分配方面的局限性。

O1-Pruner

论文，GitHub

一种基于RL的微调技术，其核心在于通过预采样评估模型的基线性能，并利用RL风格的微调机制，鼓励模型在准确性约束下生成更短的推理过程。创新性步骤：

1. 推理路径优化：针对长思维模型中存在的推理冗余现象，通过优化推理路径，减少不必要的计算步骤；
2. 动态调整推理长度：模型能够根据问题的复杂性动态调整推理的长度，使得在简单问题上输出较短的答案，而在复杂问题上则生成更为详细的推理过程；
3. 实验验证：通过在多种数学推理基准上进行实验，显著降低推理开销，提高模型准确性，展示其在处理复杂任务时的有效性。

参考

• Q-Learning