当前位置：首页 > news >正文

Shape-Guided Dual-Memory Learning for 3D Anomaly Detection 论文精读

news 2025/11/8 15:26:23

题目：Shape-Guided Dual-Memory Learning for 3D Anomaly Detection

题目：面向 3D 异常检测的形状引导双记忆学习

论文地址：ICML 2023
代码地址：https://github.com/jayliu0313/Shape-Guided
Shape-Guided 形状引导的
Dual-Memory Learning 双记忆学习
for 3D Anomaly Detection 面对3D异常检测

Abstract 摘要

我们提出一种形状引导的专家学习框架，用于解决无监督三维（3D）异常检测问题。该方法基于两个专用专家模型的有效性及其协同作用，从颜色和形状模态中定位异常区域。
第一个专家利用几何信息，通过对局部形状周围的隐式距离场建模，探测3D结构异常；第二个专家结合与第一个专家关联的2D RGB特征，识别局部形状上的颜色外观不规则性。我们利用这两个专家，从无异常的训练样本中构建双记忆库，并执行形状引导的推理，以精确定位测试样本中的缺陷。
由于采用逐点3D表示和互补模态的有效融合方案，我们的方法在MVTec 3D-AD数据集上高效实现了最先进的性能，具有更高的召回率和更低的假阳性率——这一特性在实际应用中更受青睐。

1. Introduction 引言

无监督异常检测与定位在制造业和医疗保健领域具有诸多应用。以往方法主要利用颜色信息识别输入图像中的缺陷和异常区域。虽然在大多数情况下颜色信息通常足以定位异常，但研究也表明，若充分利用三维（3D）几何信息，可助力实现更优性能（Horwitz & Hoshen, 2022）。我们的工作旨在解决最新发布的MVTec 3D-AD数据集上的3D异常检测与定位问题。我们提出形状引导的双记忆学习方法，结合颜色与几何信息，在降低计算和内存开销的同时提高异常定位精度。图1展示了我们的方法在从不同模态中精确识别缺陷方面的互补优势。
在这里插入图片描述

异常检测的性能通常通过区域级重叠率（PRO）（Bergmann等, 2021）以及异常阈值连续增加时对应的假阳性率来评估。最常见的设定是报告假阳性率高达30%时的PRO曲线下面积（AU-PRO）（即积分上限为0.3）。然而，在实际应用中，30%的假阳性率可能过高，导致无法精确识别缺陷。为解决这一问题，我们设计的方法致力于在极小的积分上限下追求更高的AU-PRO。我们的方法采用神经隐式函数（NIFs），通过有符号距离场表示局部形状，这与当前3D重建领域的方法一致（Jiang等, 2020；Takikawa等, 2021；Ma等, 2021、2022；Li等, 2022）。将点云样本划分为由NIF表示的局部块，使我们能够对存在姿态变化的复杂形状3D物体进行建模。局部有符号距离场还支持细粒度的逐点异常预测。因此，我们的方法在MVTec 3D-AD基准上实现了最先进的AU-PRO，即使在极小的积分上限下也是如此——这对于以往的2D和3D异常检测方法而言颇具挑战性。
我们将本工作的贡献总结如下：

所提出的形状引导方法有效整合了颜色和几何这两种互补模态。我们的方法内存占用更少，且推理速度更快。
我们首次提出利用有符号距离场的神经隐式函数来表示局部形状，用于3D异常检测。借助该方法，我们可以将复杂结构的3D点云建模到逐点的细粒度级别。
我们的方法在MVTec 3D-AD数据集上实现了最先进的性能，尤其是在小积分上限下，这意味着在实际应用中具备更优的召回率和更低的假阳性率，符合实际需求。

2. Related Work 相关工作

2.1 2D Anomaly Detection 二维异常检测

已有诸多方法被提出用于解决无监督二维异常检测与定位问题。大多数基于二维的方法在MVTec AD数据集上进行评估（Bergmann等, 2019; 2021），而Zheng等（2022）近期的基准测试也表明，许多无监督的基于二维的方法即使仅使用RGB信息，在MVTec 3D-AD数据集上也能表现良好（Bergmann等, 2022）。下文将简要回顾几种基于二维的方法。

2.1.1 Feature embedding-based methods 基于特征嵌入的方法

诸如（De-fard等, 2020; Lee等, 2022; Roth等, 2022）的方法在训练阶段利用预训练模型提取正常特征。在测试阶段，通过距离度量将测试特征与单个训练特征或其分布进行比较。若测试特征与训练特征存在差异，则该测试特征对应的区域更可能属于异常区域。这类方法简单直观，但在训练数据中查找对应的正常特征时可能会产生较高的计算成本。

2.1.2 Normalizing flows 基于归一化流的方法

CFLOW-AD采用带有位置编码器的条件归一化流对正常块的分布进行建模（Gudovskiy等, 2022）；其目的是基于概率密度函数分离“分布内”和“分布外”的测试块。在CSflow（Shi等, 2022）中，不同尺度的特征图由全卷积归一化流处理，将输入数据的原始分布转换为可解释的潜在空间，从而提升异常检测的准确性。

2.1.3 Student-teacher networks and simulation-based approaches 学生-教师网络和基于模拟的方法

在“不知情学生”方法中（Bergmann等, 2020），教师网络在大规模自然数据数据集上预训练以学习判别性嵌入，随后利用预训练的教师网络和无缺陷数据训练学生网络。目标是使学生网络的输出与教师网络的输出趋同。在推理阶段，两个网络的判别性嵌入之间的回归误差被用作输入数据的异常分数。并非专门针对二维异常检测的AST（Rudolph等, 2023）同时使用颜色和深度信息进行异常检测，旨在增大异常块的学生与教师输出之间的距离，这意味着异常可更容易与正常区域分离。为解决无监督异常检测中缺乏异常样本的问题，诸如（Li等, 2021; Schlüter等, 2022; Yang等, 2022）的基于模拟的方法会在正常数据上人工添加噪声以模拟缺陷，并在模拟的异常样本上训练模型。我们的方法遵循无监督异常检测的标准设定，在不依赖模拟异常样本的情况下，在MVTec 3D-AD数据集上实现了最先进的结果。

2.2 3D Anomaly Detection 三维异常检测

由于缺乏更全面的三维（3D）数据集，以往针对无监督3D异常检测的研究并不多，仅有少数方法针对3D脑部扫描中的该问题展开研究（Behrendt等, 2022; Bengs等, 2022; Viana等, 2020）。Bergmann等人引入了MVTec 3D-AD数据集（Bergmann等, 2022），用于无监督3D异常检测方法的基准测试。该数据集包含制造产品的高分辨率彩色点云。训练集和验证集仅由无异常样本组成，与实际检测场景一致。基于这些无异常样本训练的无监督方法，必须检测对应物体类别测试样本中出现的未知类型缺陷。
与以往基于彩色图像的异常检测数据集（Bergmann等, 2019; 2021）不同，MVTec 3D-AD数据集的点云表示为检测那些在彩色图像中不易识别的缺陷提供了有用的几何线索。Bergmann和Sattlegger（Bergmann & Sattlegger, 2022）提出了一个学生-教师框架，用于学习自适应几何特征以实现无监督3D异常检测，其中教师网络以自监督方式训练，从局部块中编码局部几何描述。他们在MVTec 3D-AD数据集上评估了其方法，结果表明所提出的3D学生-教师框架能够可靠地定位测试点云中的几何异常。在本工作中，我们也使用MVTec 3D-AD数据集评估所提方法，并取得了最先进的结果。
Horwitz和Hoshen使用MVTec 3D-AD数据集分析3D信息在异常检测中的实用性（Horwitz & Hoshen, 2022）。他们得出结论：“即使有颜色信息，识别异常往往也需要3D信息”。
他们的研究还表明，对局部细粒度结构进行建模的旋转不变3D表示对于3D异常检测至关重要。他们进一步提出了一种名为BTF（回归特征）的方法，结合颜色和几何模态的互补属性，在MVTec 3D-AD数据集上取得了更优结果。
我们观察到3D表示在异常检测中存在类似的问题和特性。因此，我们从点云中提取旋转不变特征，并采用隐式表示，通过有符号距离函数对细粒度的3D局部结构进行建模。此外，我们提出一种形状引导机制，有效整合颜色和几何模态，以在3D异常检测中实现最先进的性能。

3. Method 方法

与二维场景不同，用于3D异常检测的训练数据（例如MVTec 3D-AD）以两种不同的模态关联呈现，包括逐像素的RGB值和逐点的3D坐标。为充分利用这两种表示形式的互补效应，我们设计了一种形状引导的外观重建方案，该方案有效连接这两种信息流，以提高异常预测和定位的准确性。

3.1 Shape-Guided Expert Learning 形状引导的专家学习

所提方法基于两个专用专家模型的有效性及其协同作用建立，以更好地应对3D异常检测任务。第一个专家利用3D信息探测形状几何中可能存在的异常，第二个专家考虑RGB信息以识别出（颜色方面的）外观不规则性。
接下来，我们将描述这两个专家模型是如何设计和关联的。

3.1.1 Shape expert 形状专家

3D
借助逐点坐标的可用性，我们考虑设计一个3D形状专家，通过聚焦学习局部几何表示来进行异常检测。

A.以局部表示为目标的动机

我们以局部表示为目标的动机有两点：首先，缺陷或异常部分通常是局部出现而非全局出现；其次，点云局部表示的学习公式往往更具可扩展性且更高效。

B. 模型设计与训练

如图2所示，我们利用两种现有模型——PointNet（Qi等人，2017）和== （NIF）==（Ma等人，2022）——在点云应用中探索3D形状信息。
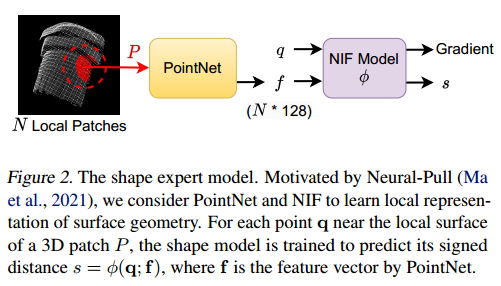
在这里插入图片描述

①局部块的特征向量
具体而言，我们首先将完整的形状点云划分为3D块，然后开展局部表示学习。对于每个生成的块，我们采样（例如）500个点，并应用PointNet来获取其特征向量，记为 $\mathbf{f}$ ，该向量编码了对应的局部几何信息。
②局部块区域表面附近采样查询点
③查询点+特征向量输入NIF获得带符号距离s
令NIF模型为 $\phi$ 。为了训练 $\phi$ 以用于异常检测，我们遵循（Ma等人，2021）中的技术，在底层3D块的表面附近采样一组查询点 $\{ \mathbf{q} \}$ ，并将这些查询点与PointNet特征 $\mathbf{f}$ 一起传入NIF模型，以预测它们的带符号距离 ${ s \}$ 。我们将查询点 $\mathbf{q} \in Q$ 相对于局部表面的带符号距离 $s$ 的预测过程表示为：
$\mathbf{q} \in Q \stackrel{\phi, \mathbf{f}}{\longrightarrow} s = \phi(\mathbf{q}; \mathbf{f}), \tag{1}$
其中，除输入 $\mathbf{q}$ 外，预测结果 $s$ 还由PointNet生成的块级特征向量 $\mathbf{f}$ 决定。

C.带符号距离函数与记忆库构建

式(1)中的每对 $\{ \phi, \mathbf{f} \}$ 构成一个带符号距离函数（SDF），可用于度量点云的局部表面几何。由于NIF $\phi$ 对所有块通用且与类别无关，在完成形状专家的学习后，我们只需将所有块级特征向量 $\{ \mathbf{f} \}$ 存储到SDF记忆库（记为 $M_S$ ）中，即可隐式编码所有“正常”的局部表示。

3.1.2 Appearance expert 外观专家

构建外观专家的目标是创建一个形状引导的记忆库 $M_A$ ，用于重建“正常”的RGB特征。
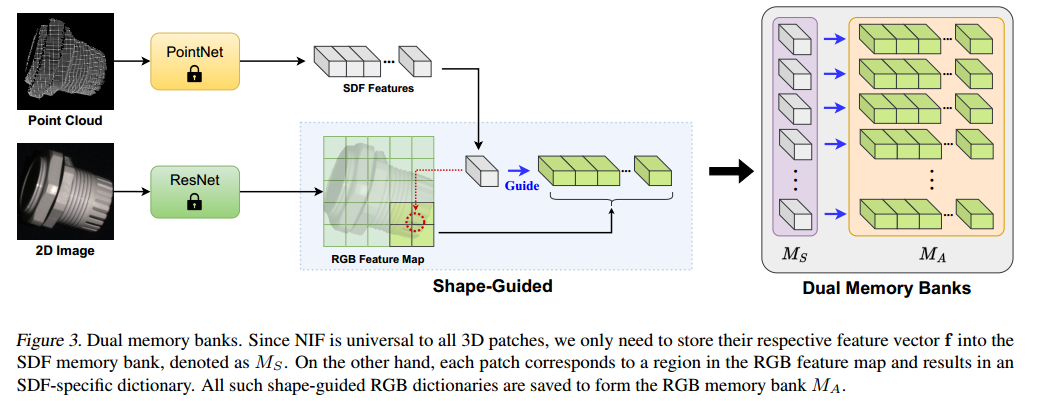
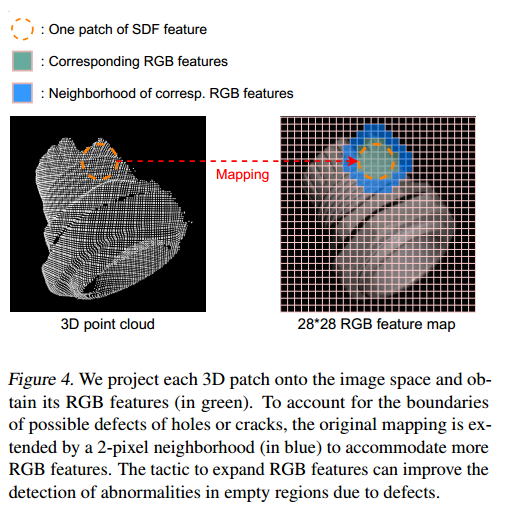
在这里插入图片描述

我们考虑点云与其2D RGB图像的配对关系（如图3所示）。在学习完形状专家后，我们可以研究带符号距离函数（SDF）与其对应RGB特征之间的映射关系。对于每个SDF，我们在3D感受野中追溯其500个采样点（即PointNet的输入），然后计算这些点的2D坐标以检索对应的RGB特征。
为了增强其在颜色外观上的表示能力，我们在特征图上对2D对应区域均匀扩展两个像素，以包含更多RGB特征（见图4）。在我们的实现中，每个SDF会对应约40到60个RGB特征向量。
如此，我们可以得到形状引导的记忆库 $M_A$ ，它包含与 $M_S$ 中SDF数量相同的、SDF专属的RGB特征字典。
在这里插入图片描述

3.2 Shape-Guided Inference 形状引导推理

借助双记忆库 $M_S$ 和 $M_A$ ，我们可以执行推理以检测测试样本 $\mathbf{x}$ 是否包含异常/缺陷（见图5）。步骤如下。
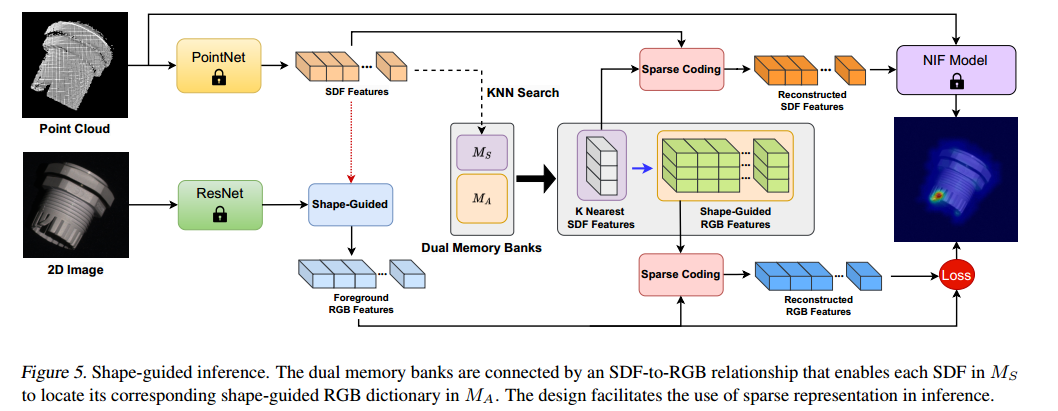
在这里插入图片描述

3.2.1 测试样本的推理

使用PointNet获取测试样本 $\mathbf{x}$ 的所有块级带符号距离函数（SDF），即 $\{\tilde{\mathbf{f}}\}$ 。
使用ResNet获取 $\mathbf{x}$ 的RGB特征图。在2D RGB图像中，与至少一个SDF相关联的像素被视为前景。
对于 $\{\tilde{\mathbf{f}}\}$ 中的每个SDF，在 $M_S$ 中找到其 $k_1 = 10$ 个最近邻，以形成相应的字典，并通过稀疏表示获得其近似值 $\hat{\mathbf{f}}$ 。
对于 $\mathbf{x}$ 的每个块，使用块级重建的 $\hat{\mathbf{f}}$ 计算其感受野内所有3D点 $\{\hat{\mathbf{q}}\}$ 的带符号距离，即 $\phi(\hat{\mathbf{q}}; \hat{\mathbf{f}})$ 。
采用 $\mathbf{x}$ 所有块的带符号距离的绝对值，形成最终的SDF分数图。
对于步骤3中用于计算稀疏表示的 $M_S$ 中所有相关SDF，将它们在 $M_A$ 中关联的所有RGB字典取并集，形成形状引导的RGB字典，记为 $\hat{D}$ 。
对于步骤2中每个前景RGB特征向量，从 $\hat{D}$ 中找到其 $k_2 = 5$ 个最近邻，并获得其稀疏表示。由近似值产生的 $\ell_2$ 距离构成最终的RGB分数图。
执行分数图对齐（下文将描述），并在像素级别取SDF和RGB响应的最大值作为对应的异常分数。

3.2.1 Score-map alignment 分数图对齐

通过最大池化融合 SDF和RGB分数图时，要求两者的数值处于可比较的范围。由于训练阶段没有异常样本可用于估计合适的统计量，我们通过对25个随机选取的训练样本模拟推理，并采用 “自排除”策略来模拟测试结果，以此克服这一难题。该策略会在测试步骤的最近邻搜索中，排除查询样本自身的SDF和RGB特征。为了对齐这两个结果的分数分布，我们考虑映射 $\mapsto a \times y + b$ ，使得RGB分数分布的均值±3倍标准差映射到其对应的SDF分数分布的均值±3倍标准差。得到的缩放参数 $a$ 和偏移参数 $b$ 可直接用于将RGB分数 $y$ 校正为 $\times y + b$ 。

3.2.2 从单类别到统一的验证

最后需要说明的是，到目前为止，我们的公式仅针对单类别 3D异常检测进行了阐述。
尽管如此，考虑到MVTec 3D-AD的十个物体类别区分度极高，且我们实现的分类器确实达到了100%的分类准确率，因此我们的方法本质上为MVTec 3D-AD上的异常检测提供了一种统一的解决方案。

4. Experiments 实验

4.1 Experimental Setup 实验设置

4.1.1 Dataset 数据集

我们在MVTec 3D-AD（Bergmann & Sattlegger, 2022）上评估我们的方法，该数据集提供了十个不同类别的3D物体，用于2D+3D异常检测。MVTec 3D-AD包含2656个训练样本、294个验证样本和1197个测试样本。训练和验证数据无任何缺陷，而测试数据分为249个正常样本和948个异常样本。异常测试样本在每个类别中包含约4到5种不同类型的缺陷。
MVTec 3D-AD与之前的2D-AD数据集不同：每个样本都配备高分辨率点云和对应的RGB图像。我们提出的方法旨在充分利用重要的2D和3D模态，以在缺陷检测中获得更优性能。
我们将训练数据的每个点云样本划分为块，以丰富形状多样性，并利用这些块训练PointNet和NIF模型。随后，带有相关RGB模态的相同训练样本被用于构建双记忆库。

4.1.2 Preprocessing 预处理

先分块再下采样➡既有原始点也有空间下采样的点
点云的预处理包含若干步骤。首先，我们遵循基线方法BTF（Horwitz & Hoshen, 2022），移除整个数据集中的背景点云。接下来，我们根据下一段中描述的局部块提取流程，提前准备好训练和测试样本的裁剪块的npz文件。用于训练和测试的npz文件包含3D点及其对应的2D索引，而用于训练PointNet和NIF的npz文件则同时包含空间下采样的点和原始点。
此外，我们将原始点云和图像的分辨率从800×800分别调整为224×224，点云使用最近邻插值，图像使用双三次插值，与基线方法（Horwitz & Hoshen, 2022）一致。

4.1.3 Local patches 局部块

此前的方法PCP（Ma等人，2022）和LIG（Jiang等人，2020）通过将点云划分为若干局部区域，表现出了良好的性能。隐式神经特征学习领域的近期进展也推动了点云局部结构的分析与建模。我们的方法同样将整个点云划分为局部块，以对其局部结构进行建模。
受Point-MAE（Pang等人，2022）的启发，我们采用最远点采样（FPS） 从原始点云中采样一组点，随后以每个FPS点为中心，在其感受野内寻找K近邻，从而形成一个局部块。需要注意的是，原始点云中的单个点可能被多个FPS点视为K近邻，即局部块之间可能存在重叠，以共享部分邻域。由于块的重叠性，我们动态调整采样集的大小（即FPS点的数量），以确保局部块的并集尽可能多地覆盖原始点云。

4.1.4 Parameter settings 参数设置

我们将每个点云样本划分为重叠的3D局部块。每个局部块包含500个点（ $K = 500$ ）。我们确保局部块的数量足够多，以共同覆盖点云样本中的所有点。例如，我们选择重叠率为10，这样对于一个包含约7500个点的点云样本，可得到大约150个局部块（计算方式为“重叠率×总点数÷单个局部块的大小”，即 $10 \times 7500/500 = 150$ ）。
在训练PointNet和NIF的预处理步骤中，我们如PCP（Ma等人，2022）的做法，在每个真实点周围仅采样20个查询点。我们将学习率和批量大小分别设置为0.0001和32，这在经验上实现了高效收敛。

4.2 Implementation Detail 实现细节

4.2.1 Training the experts 专家模型的训练

我们使用训练样本训练一个简化的PointNet ，用于从局部块中提取3D特征；同时微调在ImageNet上预训练的ResNet ，以提取28×28的RGB特征图。
我们还训练了一个神经隐式函数（NIF），用于从PointNet提取的3D特征中推导带符号距离函数（SDF），如图2所示。
该简化的PointNet由三个卷积层和两个全连接层组成，每层均包含批量归一化。NIF模型是一个多层感知机，用于刻画局部几何的潜在形状。
我们用于RGB线索的2D模型采用了Wide ResNet-50-2（Zagoruyko & Komodakis, 2016），与PatchCore（Roth等人, 2022）中的设置一致；我们从第一层和第二层提取特征并进行融合。

4.2.2 Score alignment 分数对齐

RGB特征的尺度与SDF特征的尺度差异显著，这会导致分数分布不同。我们需要在融合分数前对这两种分布进行校准。
我们随机选取25个训练样本，在像素级测试前模拟分数分布。为了校准分数分布，我们对RGB分数应用仿射变换，使RGB分数的均值±3倍标准差与SDF分数的均值±3倍标准差对齐。
测试时，我们使用预先计算的仿射变换的权重和偏置，将RGB分数与SDF分数对齐。最终，我们可通过逐像素取最大值的方式直接融合这两个分数图。

4.3 Evaluation Metrics 评估指标

① I-AUROC && P-AUROC
我们采用受试者工作特征曲线下面积（AUROC） 来评估所提方法在图像级（Img-AUROC） 和 像素级（Pix-AUROC） 的性能。
② P-AUPRO
为了更精确地评估MVTec 3D-AD数据中每个像素的预测结果，我们使用区域重叠率（PRO）（Bergmann等人，2021），并计算PRO曲线下面积（AUPRO），将其作为利用生成的异常分数和真实连通区域进行异常定位的评估指标。

4.4 Experimental Results 实验结果

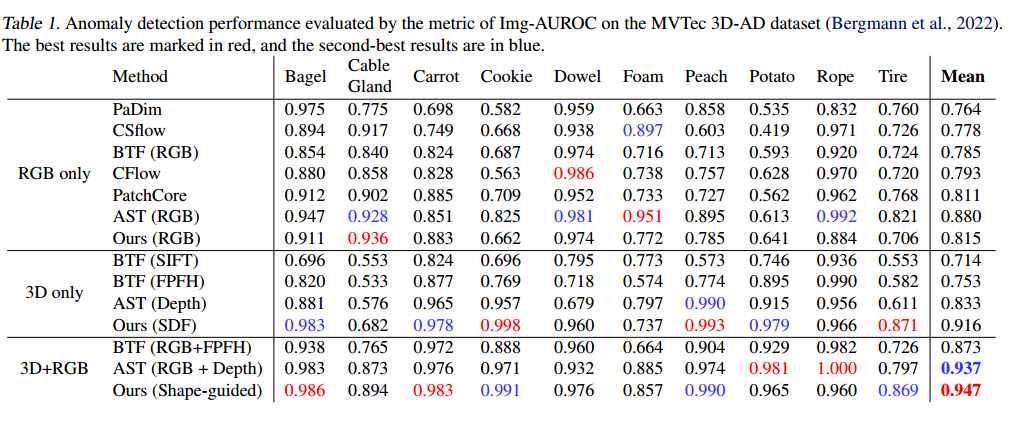
I-AUROC
表1在MVTec 3D-AD数据集上比较了我们的方法与现有方法，采用Img-AUROC指标进行评估。我们将我们的方法与PaDim（Defard等人，2020）、CSflow（Shi等人，2022）、BTF（Horwitz & Hoshen，2022）、CFlow（Gudovskiy等人，2022）、PatchCore（Roth等人，2022）、AST（Rudolph等人，2023）和3D-ST（Bergmann & Sattlegger，2022）进行比较。
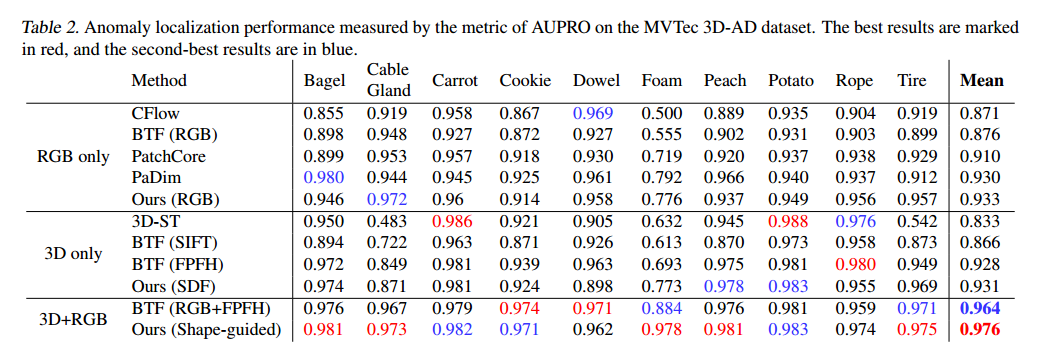
在这里插入图片描述

AUPRO
表2采用AUPRO 指标展示了异常定位性能，其中我们计算了PRO值 在假阳性率（FPRs） 上的积分。与大多数先前的方法一样，我们将0.3作为FPR积分上限。更小的FPR积分上限意味着我们对假阳性的容忍度更低。
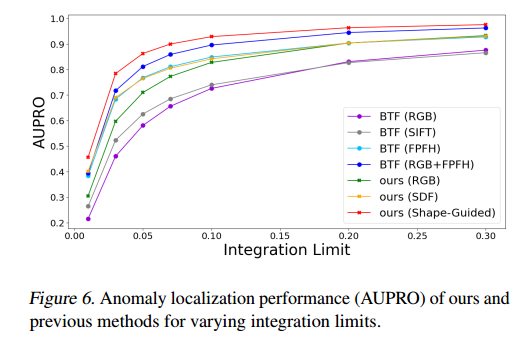
由于在实际场景中，低积分上限下的异常定位性能更为关键，我们在图6中针对七个不同的积分上限{0.3,0.2,0.1,0.07,0.05,0.03,0.01}，将我们的方法与现有方法进行了比较。结果表明，我们的方法在标准积分上限0.3和极低积分上限下均取得了最先进（state-of-the-art） 的性能。
在这里插入图片描述

在这里插入图片描述

4.5 Computational Complexity 计算复杂度

4.5.1 Inference time and memory usage 推理时间与内存占用

推理性能和内存占用在工业应用中至关重要。我们的带形状引导机制的方法仅需较低内存占用，即可在像素级和图像级预测中取得最先进的结果，如表3所示。我们展示了我们的方法和BTF方法的单样本平均推理时间以及平均RGB内存占用。
在这里插入图片描述

A. 平均RGB内存占用

BTF采用PatchCore方法对核心集的特征进行10%的子采样，其中10%是PatchCore中最常见的设置。需要注意的是，RGB特征占用的内存远大于SDF特征占用的内存，且RGB查询的推理时间也远长于SDF查询的推理时间，因此我们仅对与RGB相关的计算进行比较。

B.单样本平均推理时间

我们还纳入了推理速度（以每秒帧数（fps）衡量）以及在单个测试样本上检测异常时 最近邻（NN）搜索涉及的特征数量。我们的形状引导机制助力在0.69 fps的最快速度下，取得最优的AUPRO（0.3）和AUPRO（0.01）性能。

4.5.2 Detailed analysis 详细分析

异常检测器的计算复杂度可通过考察其在GPU和CPU上执行的计算来评估。GPU主要通过ResNet或PointNet等模型处理特征提取任务。
在GPU和CPU上执行的计算次数
例如，我们用于提取RGB特征的ResNet模型需要5.0 GMACs（十亿次乘加运算）和413万参数；而我们用于点云的SDF模型（PointNet + NIF）需要1.29 GMACs和317万参数。
相反，BTF遵循PatchCore的设计，仅对RGB特征采用ResNet模型，其计算需求为5.0 GMACs和413万参数。总体而言，我们的方法比BTF多需要约25%的GMACs。
尽管如此，我们发现后续操作（如CPU执行的k近邻（kNN）特征搜索）对异常检测算法的总计算成本起主导影响作用。BTF中的FPFH表示也需要额外的CPU计算。
因此，对异常检测（AD）算法计算成本的更全面比较，需结合GPU的GMACs/FLOPs，同时评估其整体推理时间和内存占用。

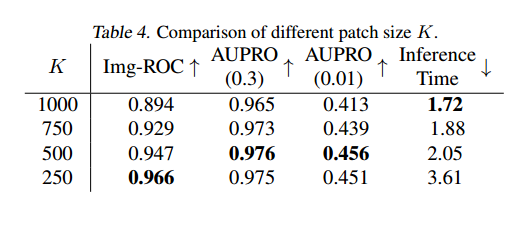
4.6 Patch Size Analysis 块大小分析

我们针对不同的块大小 $K$ 评估我们的方法，结果列于表4。增大 $K$ 的值对应着将点云划分为更大尺寸的重叠3D块。可以发现，大的块尺寸具有覆盖异常发生完整区域的优势，但同时可能使带符号距离函数（SDF）难以正确编码局部3D表面几何结构。出于推理效率和准确性的考虑，我们选择将 $K$ 设为500。
在这里插入图片描述

4.7 Qualitative Results 定性结果

4.7.1 Comparison with other methods 与其他方法的比较

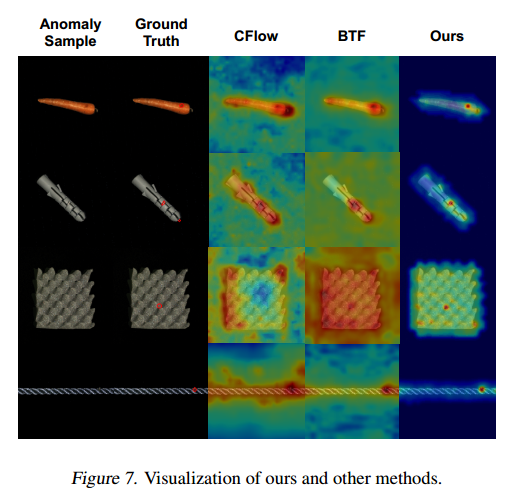
图7表明，我们的方法在精准定位异常区域方面优于其他方法。即使在低积分上限下，我们的方法也表现出色。
在这里插入图片描述

4.7.2 Benefits of cross-modality 跨模态的优势

我们在图8中提供了更多定性结果。我们强调了我们方法中外观专家和形状专家的互补性。专家上的绿色对勾（√）表示该专家对异常区域有响应，而红色叉号（X）表示该专家无响应。我们的融合方案受益于这种互补性，能够在最终分数图上成功识别异常区域。
在这里插入图片描述

4.7.3 Failure cases 失败案例

我们的方法结合了RGB和3D点云的优势，使它们在异常检测中形成互补。因此，若两者均无法有效检测异常，性能将低于预期。在图9中，我们的大多数失败案例出现在难以检测的隐匿异常上，现有方法在这类数据上也表现不佳。
在这里插入图片描述

5. Additional Ablation 额外消融实验

5.1 Benefit of Combining RGB and 3D Information 结合RGB和3D信息的优势

在MVTec 3D-AD数据集中，大多数异常同时出现在几何结构和颜色上。然而，有些异常仅出现在两种模态中的一种。如之前图1所示，基于2D颜色的方法无法检测几何异常（例如类似巧克力片的饼干孔洞，这类异常无法通过颜色线索明确检测）；另一方面，泡沫上的变色缺陷也无法通过纯3D方法检测。因此，我们采用所提出的双专家学习和RGB与SDF分数的分数对齐策略，以结合两种模态的优势。
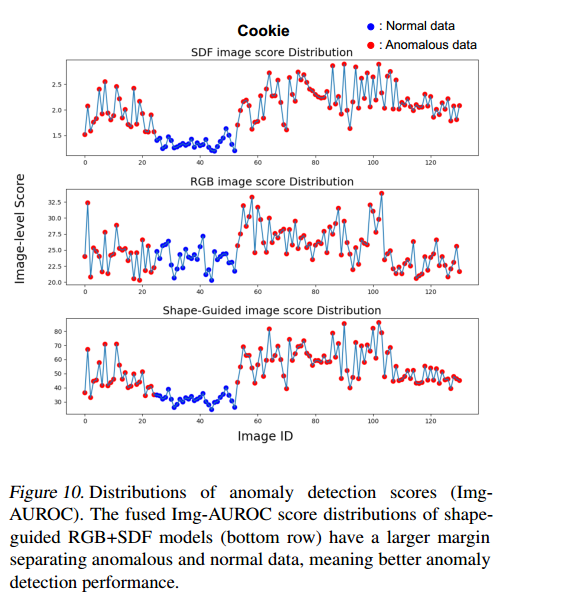
在表5中，我们比较了我们的方法与仅用RGB、仅用SDF以及仅用形状引导RGB方法的AUPRO分数。图10也显示，结合后的Img-AUROC分数在异常与正常数据分布之间呈现显著差距。从这些实验结果可以看出，我们的双专家模型通过有效结合基于2D颜色和基于3D几何的信息，其协同作用提升了性能。
在这里插入图片描述

在这里插入图片描述

5.2 The Effectiveness of Sparse Coding 稀疏编码的有效性

我们并未直接计算目标特征与其在记忆库中最近特征的距离来作为异常分数，而是采用稀疏编码对RGB和SDF特征的目标特征进行重构。
由于稀疏编码使用从记忆库中正常特征衍生的字典，因此稀疏表示能够准确描述无异常特征。这种稀疏表示有助于从无缺陷局部区域提取的特征更好地泛化到其重构对应特征，从而使我们能更可靠地区分正常与异常。
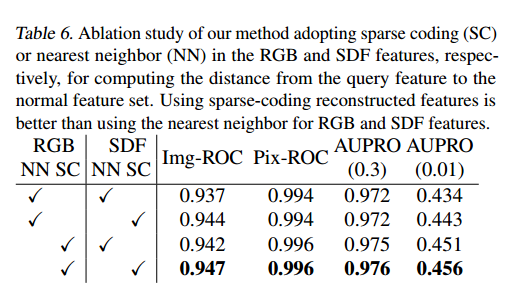
表6展示了在RGB和SDF特征中分别采用稀疏编码或最近邻方法，计算查询特征到正常特征集距离的结果。结果表明，对于RGB和SDF特征，使用稀疏编码的重构特征比使用其最近邻的效果更优。
在这里插入图片描述

6. Conclusion 结论

我们提出了一种新方法，在MVTec 3D-AD数据集上实现了无监督3D异常检测的最先进（state-of-the-art） 性能。我们的方法具有更高的召回率和更低的假阳性率，这在需要精准定位缺陷的实际应用中更具优势。
此外，所提出的框架具有高效性，我们对双记忆库和形状引导推理的实现显著降低了计算和内存成本。我们已经证明，使用神经隐式函数对3D局部形状进行建模，在检测点云的细微不规则性方面具有极大优势。
本工作还提供了融合不同模态预测的实用技术，结合新的形状引导专家学习框架，可能为无监督3D异常检测任务的未来发展带来益处。