拓扑排序深入

拓扑排序

一、前言

今天带来图的另外一种算法——拓扑排序。可是这和我们常见的排序一样吗？在图中有怎样的新的表达呢？

二、拓扑排序

在图中的拓扑排序当然和线性结构的排序（冒泡/快速/交换等）完全不同。

它的存在受制于图，也被图赋予了特殊的含义，在现实生活中也表现出独特的性质。

比如说，在工程中，必须先有需求分析，才能制作功能流程图，其次设计架构，最后才可以进行项目开发。每件事情并非独立，而是具有一定的先后次序的；还有在闯关游戏中，必须通过当前关卡的游戏才能解锁下一关一样，关卡的设置和游戏的难易程度相关）。

拓扑排序的出现就是为了找到一种合理的完成事情的顺序。

当然这只是拓扑排序的物理含义，抽象成模型是怎样的呢？

2.1 导入

2.1.1 有向无环图

拓扑排序的抽象模型就是有向无环图。

相信经过图的概述一篇，你肯定已经明白了有向无环图的定义。

放个图。

为什么一定是有向无环图呢？

使事情具有先后顺序（优先级），这不就是有向图吗？为什么是无环？这是为了保证顺序的可行性，防止形成死锁。

那如何判断一个图有没有环呢？

在$Kruskal$​算法中，我们曾使用并查集来排除成环的可能性

在这里有了一种新的方式。（先卖个关子~）

2.1.2 活动

每一个小步骤就是一个活动（在图中就是顶点）。

2.1.3 $AOV$​网

$Activity$ $On$ $Vertex$ $Network$，在一个图中，顶点表示活动，弧（有方向的边）表示活动的优先关系，称为$AOV$网。

活动的优先关系：弧尾的活动完成之后，才能去完成弧头的活动。

2.1.4 拓扑序列

一个路径中，有顶点在前，有顶点在后，从而形成的有顺序的顶点排列就是拓扑序列。

2.2 拓扑排序

2.2.1 定义

对一个有向无环图进行顶点的序列化处理

2.2.2 思想

对于一组有先后依赖关系的任务（或节点），找到一个线性的执行序列，使得任何任务都不会在其所依赖的所有前置任务完成之前开始。

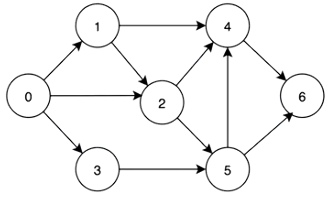
如图：

阐释：

一眼看过去。只有0没有依赖项，于是从0开始。0任务结束后，1，3都可以进行了。2为什么不行呢？2可是有两个依赖指向呢——0和1，必须0和1都完成才可以进行任务2。就这样，依次类推。

2.2.3 步骤

所谓依赖就是入度，因此拓扑排序核心为维护入度数组。

• 找到图中，入度为0的顶点，把这些顶点放入缓存区（栈/队列）

  一开始，一定有一个入度为0的顶点，是整个任务的伊始。

  这里的缓存区，我们采用栈。栈只需维护一个栈顶指针，但是队列需要维护队首和队尾两个指针。

• 从缓存区中取出一个顶点，放入结果集，这个顶点的任务执行完毕

• 顶点的出度对应的其余顶点的入度清零——解放依赖

• 在清零的过程中，查找入度为0的顶点（两个事同时进行），如果有，继续放入缓存区（推进任务进度）

• 重复2，3，4

• 缓存区为空时，结果集中的顶点个数和实际图中顶点的个数，如果相等（任务都顺利完成啦），则没有环（判断成环的方法）

2.2.4 图示模拟

既然是有向图，存储结构首选邻接表（这里是正邻接表）

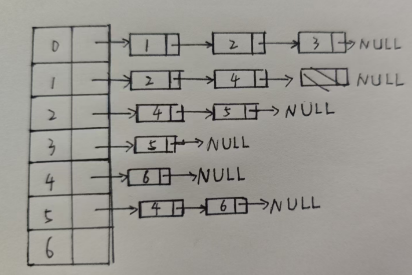
既然要找入度为0的顶点，不能一遍又一遍地遍历邻接表，因此，不如只遍历一遍得到一个入度记录表，当想找入度为0的点时，只需遍历一遍入度记录表更好（可以用优先级队列），这样效率更高一些。

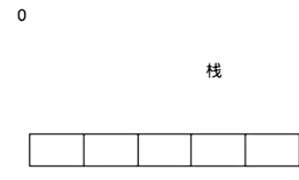
栈结构

模拟：

• 找到入度为0的点，入栈

• 出栈

• 清零入度表

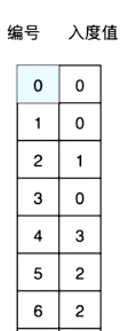
• 继续入栈（和上一步是同时进行的）
  
• 循环上述操作

2.2.5 代码

拓扑排序基于邻接表实现，先前已经实现了邻接表，在这里不再赘述了，直接采用其接口，详情见邻接表

// 拓扑排序，返回1表示有向无环，0表示无环，-1表示错误
int TopologicalSortAGraph(const AGraph *adjacencyList)	// 排序无需改变邻接表-const
{// 准备工作// 定义一个入度记录表，便于发现入度为0时，放入缓存区int *inDegree;inDegree = malloc(sizeof(int) * graph->nodeNum);if(inDegree == NULL){return -1;}memset(inDegree, 0, sizeof(int) * graph->nodeNum);// 初始化入度记录表// 遍历邻接表for(int i = 0; i < graph->nodeNum; i++){if(graph->nodes[i].firstEdge)			// 说明i节点开始有边{ArcEdge *edge = graph->nodes[i].firstEdge;while(edge){++inDegree[edge->no];edge = edge->next;}}}// 查找入度记录表，度为0的顶点，设计一个链式栈的缓存区，更新入度记录表时，发现0，就放入任务栈// 设计栈int *stack = malloc(sizeof(int) * graph->nodeNum);if(stack == NULL){free(inDegree);return -1;}int top = -1;// 入栈for(int i = 0; i < graph->nodeNum; ++i){if(inDegree[i] == 0){stack[++top] = i;}}// 根据任务栈里的数据，弹出第一个任务，这个任务对应的节点相关的入边个数删除// 更新任务记录表，如果更新过程中，发现入度为0，直接入栈int index;while(top != -1){index = stack[top--];count++;visitAGraphNode(&graph->nodes[index]);// 更新入度信息ArcEdge *edge = graph->nodes[index];while(edge){--inDegree[edge->no];if(inDegree[edge->no] == 0){stack[++top] = edge->no;}edge = edge->next;}}// 释放free(inDegree);free(stack);// 判断是否有环if(count == graph->nodeNum){return 0;}else{return 1;}
}

三、小结

所谓拓扑排序，不过是将生活中的事件抽象成一个物理模型，从而解决更多复杂的问题——关于将大事件拆分成小活动（步骤）完成，找到小活动的优先顺序，从而更加高效地解决问题。

这为我们的生活提供了 不少启示，不是吗？

下一篇，我将介绍一种图的新的应用，让我们一起揭开图更多的秘密吧~