当前位置：首页 > news >正文

从`im2col`到Ascend C：深度解析昇腾CANN中的卷积(Conv2D)算子实现

news 2025/11/7 17:03:44

前言

在之前的文章中，我们通过一个简单的Add算子，成功走通了CANN算子开发的完整流程。那是一次精彩的“启蒙之旅”。然而，Add算子的计算逻辑和内存访问模式都相对简单。在真实的深度学习模型中，占据计算量大头的，是那些结构更复杂、优化空间更广阔的核心算子。

卷积（Convolution, Conv2D），无疑是这个世界里的“王者”。它是计算机视觉的基石，几乎所有图像相关的模型（从LeNet到ResNet，再到Vision Transformer之前的CNN主干）都构建于卷积之上。因此，理解并能亲手实现一个高性能的卷积算子，是衡量一位AI系统工程师硬核实力的重要标准。

本文将带领你深入卷积算子的“引擎室”，剖析其在昇腾NPU上实现高性能的核心思想——im2col + GEMM策略，并结合Ascend C编程模型，为你揭示理论与代码之间的精妙联系。

第一章：卷积的本质与硬件实现的困境

1.1 卷积的数学直觉

从数学上看，二维卷积是一个在输入特征图（Feature Map）上进行滑动窗口加权求和的过程。一个小的权重矩阵，我们称之为卷积核（Kernel）或滤波器（Filter），在输入图上从左到右、从上到下滑动。在每一个位置，卷积核的元素与输入图上对应位置的元素相乘，然后将所有乘积相加，得到输出特征图上的一个像素点。

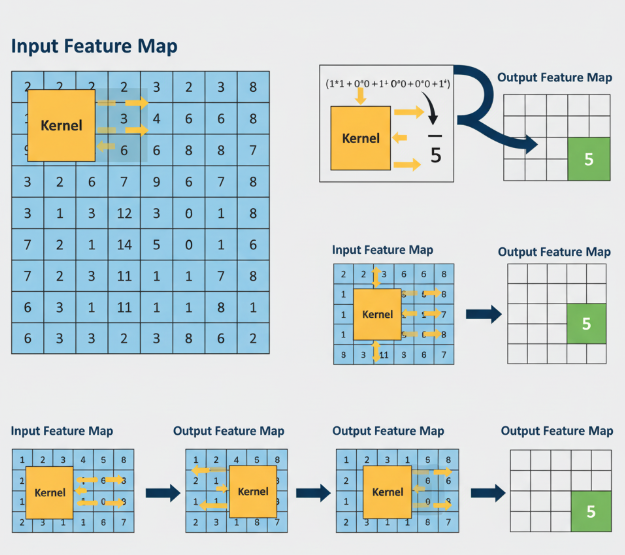
![image.png](https://i-blog.csdnimg.cn/img_convert/602f9ca48c512d6d5da225cae4ea3b80.png)

这个过程优雅地实现了局部特征提取，但它给硬件实现带来了一个巨大的噩梦。

1.2 硬件的噩梦：非连续内存访问

现代处理器（无论是CPU、GPU还是NPU）的性能，都高度依赖于连续的、可预测的内存访问。这样，硬件的预取（Prefetch）机制才能生效，数据才能像流水一样被送入计算单元。

而卷积的滑动窗口特性，彻底破坏了内存访问的连续性。当计算输出特征图的第一个点时，我们需要读取输入图的左上角一块数据；计算第二个点时，窗口向右滑动一个步长（stride），又需要读取一块部分重叠但起始地址不同的数据。这种跳跃式、非对齐的内存访问模式，会频繁导致缓存失效（Cache Miss），让数据总是在“路上”，而强大的计算单元却在“挨饿”，硬件利用率极低。

直接用多层嵌套循环来实现滑动窗口，是一种“暴力”但性能极差的方法。那么，高性能计算库（如cuDNN, MKL-DNN, CANN）是如何解决这个问题的呢？答案是一种优雅的工程魔法——im2col。

第二章：`im2col` + `GEMM`：化腐朽为神奇的核心策略

2.1 im2col (image-to-column) 的“空间换时间”

im2col是一种数据重排（Data Re-layout）技术，其核心思想是**“用空间换时间”**。它通过消耗额外的内存，将卷积操作中所有非连续的内存访问，预处理成一次性的、连续的内存访问。

具体来说，im2col将卷积操作转化为两个步骤：

转换输入特征图： 对于输出特征图上的每一个像素点，我们都找到它在输入特征图上对应的那个“感受野”（即与卷积核大小相同的区域）。然后，我们将这个二维的感受野拉直（flatten）成一个列向量。最后，将所有输出点对应的列向量拼接在一起，形成一个巨大但结构规整的中间矩阵A。
转换卷积核： 将所有的卷积核（假设有N个）也逐一拉直，形成另一个中间矩阵B。

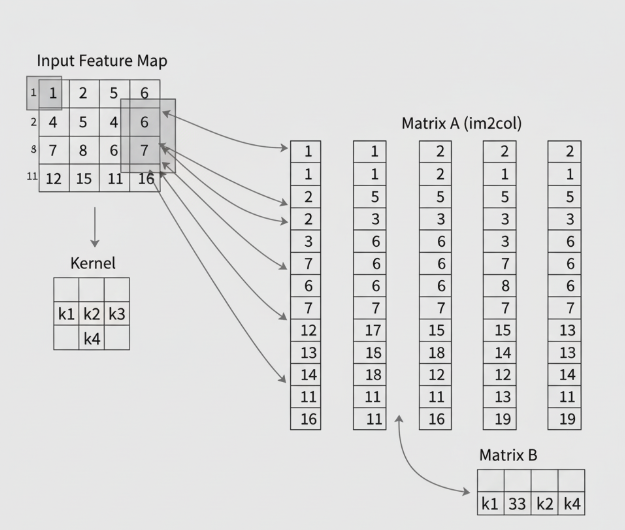
图2说明： im2col转换的核心过程——将输入图的局部块拉直成列，构成新矩阵。

2.2 `GEMM` (General Matrix Multiplication)：通往性能巅峰的康庄大道

经过im2col的“乾坤大挪移”之后，神奇的事情发生了：
原来复杂的卷积运算，现在等价于这两个新生成的中间矩阵A和B的矩阵乘法 (C = B * A)！
输出矩阵C的每一列，正好对应输出特征图上每一个通道的所有像素值。

这个转换的意义是革命性的：

计算密集： 我们将一个访存密集型（Memory-bound）的操作，转换成了一个计算密集型（Compute-bound）的操作。
硬件友好： 矩阵乘法是计算机体系结构中被优化得最彻底的运算。几乎所有的AI芯片都为其设计了专门的硬件单元。
昇腾的绝配： 对于昇腾Da Vinci架构而言，这意味着我们可以直接动用其最强大的武器——立方计算单元（Cube Unit）。这个巨大的脉动阵列，就是为了以最高吞吐率执行矩阵乘法而生的。

通过im2col，我们成功地将卷积问题，转化为了昇腾硬件最擅长解决的问题。这就是高性能卷积算子实现的基石。

第三章：Ascend C 实现卷积算子的关键考量

现在，我们知道了“做什么”，接下来要解决“怎么做”。在Ascend C中实现一个基于im2col的卷积算子，我们需要将问题进一步分解。

3.1 Tiling策略的演进：从一维到二维

对于Add算子，我们是在一维的总长度上进行Tiling。但对于矩阵乘法 C(M, K) = A(M, N) * B(N, K)，Tiling变得更加复杂。为了将计算任务均匀地分配给多个AI Core，并有效利用Local Memory，我们通常在输出矩阵C的维度上进行二维Tiling。

例如，我们可以将输出矩阵C切分成多个block_M * block_K大小的瓦片（Tile）。每个AI Core负责计算其中的若干个瓦片。为了计算一个C的瓦片，我们需要从Global Memory中加载A矩阵对应的block_M * N行条带和B矩阵对应的N * block_K列条带。

3.2 `im2col`本身的实现

im2col本身也是一个计算任务，它涉及大量的内存读写。在CANN中，im2col可以：

作为一个独立的预处理算子实现： 先在NPU上运行一个im2col算子，将整个中间矩阵A显式地生成在Global Memory中。这样做的好处是逻辑简单，但会消耗巨大的额外内存，并带来两次全局内存读写（一次写im2col结果，一次MatMul读）。
融合在卷积核函数内部（On-the-fly im2col）： 这是更优化的方法。在计算每个C矩阵的瓦片时，**即时地（on-the-fly）**在Local Memory中生成当前计算所需要的A矩阵的行条带。这样避免了在全局内存中物化整个巨大的中间矩阵，极大地节省了内存和带宽。

3.3 Ascend C 核心代码逻辑（代码与解读）

一个完整的卷积核函数非常复杂。我们在此展示其核心的、简化的Process函数逻辑，以揭示其工作流程。我们假设采用更简单的“独立im2col”策略。

// 代码: 卷积核函数的核心Process逻辑
__aicore__ inline void Process() {// 1. Tiling on Output Matrix C: //    根据blockIdx和blockNum，计算当前AI Core负责计算的输出矩阵C的瓦片(Tile)的起始位置(m_start, k_start)和循环步长。// 2. Main Tiling Loopfor (int m = m_start; m < M; m += m_step) {for (int k = k_start; k < K; k += k_step) {// 当前需要计算的输出瓦片是 C[m:m+block_M, k:k+block_K]// 3. Copy-In Stage://    - 从Global Memory加载im2col后的A矩阵的一个行条带到Local Memory//      DataCopy(a_local, a_gm[m * N], block_M * N);//    - 从Global Memory加载权重矩阵B的一个列条带到Local Memory//      DataCopy(b_local, b_gm[k], N * block_K); // 注意B矩阵的内存布局// 4. Compute Stage://    - 在Local Memory中，调用MatMul指令，这是最关键的一步！MatMul(c_local, a_local, b_local, block_M, N, block_K);// 5. Copy-Out Stage://    - 将计算完成的c_local瓦片写回到Global Memory的正确位置//      DataCopy(c_gm[m * K + k], c_local, block_M * block_K);}}
}

代码解读：

二维循环： Tiling循环不再是一维，而是变成了在输出矩阵的行（M）和列（K）维度上的嵌套循环。
数据块加载： CopyIn阶段需要精确计算源地址，从a_gm和b_gm加载对应的矩阵子块。
核心计算MatMul： MatMul是Ascend C提供的强大指令（Intrinsic），它会直接调用AI Core内部的立方计算单元（Cube Unit），以硬件支持的最高效率完成c_local = a_local * b_local的计算。这行代码就是性能的来源。

第四章：超越基础：卷积算子的优化深水区

实现了基础功能后，真正的性能优化之旅才刚刚开始。

4.1 数据排布（Layout/Format）的魔力

为了让Cube Unit的计算效率达到极致，输入的数据并非以常规的NCHW格式存放在内存中。CANN内部会将其重排布为一种称为分形（Fractal）或NZ的特殊格式。这种格式可以确保矩阵乘法在硬件层面以最高效的流水线方式进行。作为算子开发者，我们需要了解并能处理这些特殊的数据格式，这通常通过CANN提供的API来完成。

4.2 其他卷积算法：Winograd与FFT

虽然im2col + GEMM是最通用、最强大的卷积实现策略，但并非唯一。在某些特定场景下（如3x3的小卷积核、stride为1），Winograd算法可以通过更少的乘法次数实现卷积，从而获得更高的性能。对于大的卷积核，基于**快速傅里叶变换（FFT）**的卷积算法在理论上更优。一个完备的算子库，会根据输入的参数（如kernel_size, stride等），智能地选择最优的实现算法。

4.3 融合的力量

正如第一章所述，将卷积和后续的激活函数（如ReLU）融合成一个算子，是图引擎最爱的优化。在我们的算子实现中，可以在MatMul计算完成、结果仍在Local Memory时，紧接着调用向量指令对其进行ReLU操作，然后再CopyOut回Global Memory。这避免了一次代价高昂的全局内存往返，是提升端到端性能的关键。