基础数学算法

质数

试除法判定质数

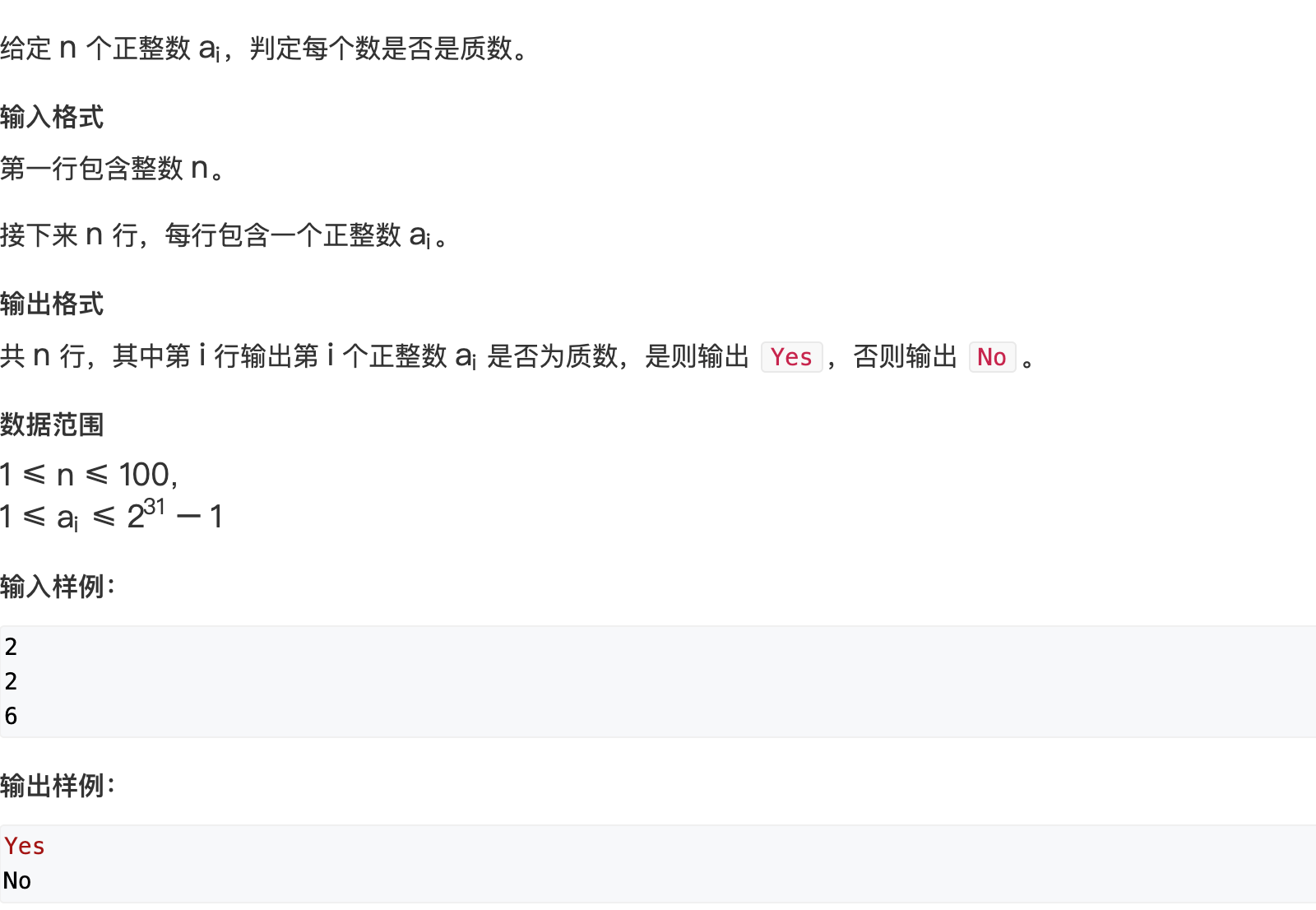
根据定义$[1,n]$中与$n$互质的数的个数只有$1$和他本身, 也就是约数个数为$0$
, 因为约数是成对出现的, 只需要枚举较小的约数, 也就是$d\le \frac{n}{d}$, 推理得到$d^2\le n$, 算法时间复杂度$O(\sqrt{n})$

#include <bits/stdc++.h>using namespace std;int n;bool is_prime(int val) {if (val < 2) return false;for (int i = 2; i <= val / i; ++i) {if (val % i == 0) return false;}return true;
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n;while (n--) {int val;cin >> val;cout << (is_prime(val) ? "Yes" : "No") << '\n';}return 0;
}

分解质因数

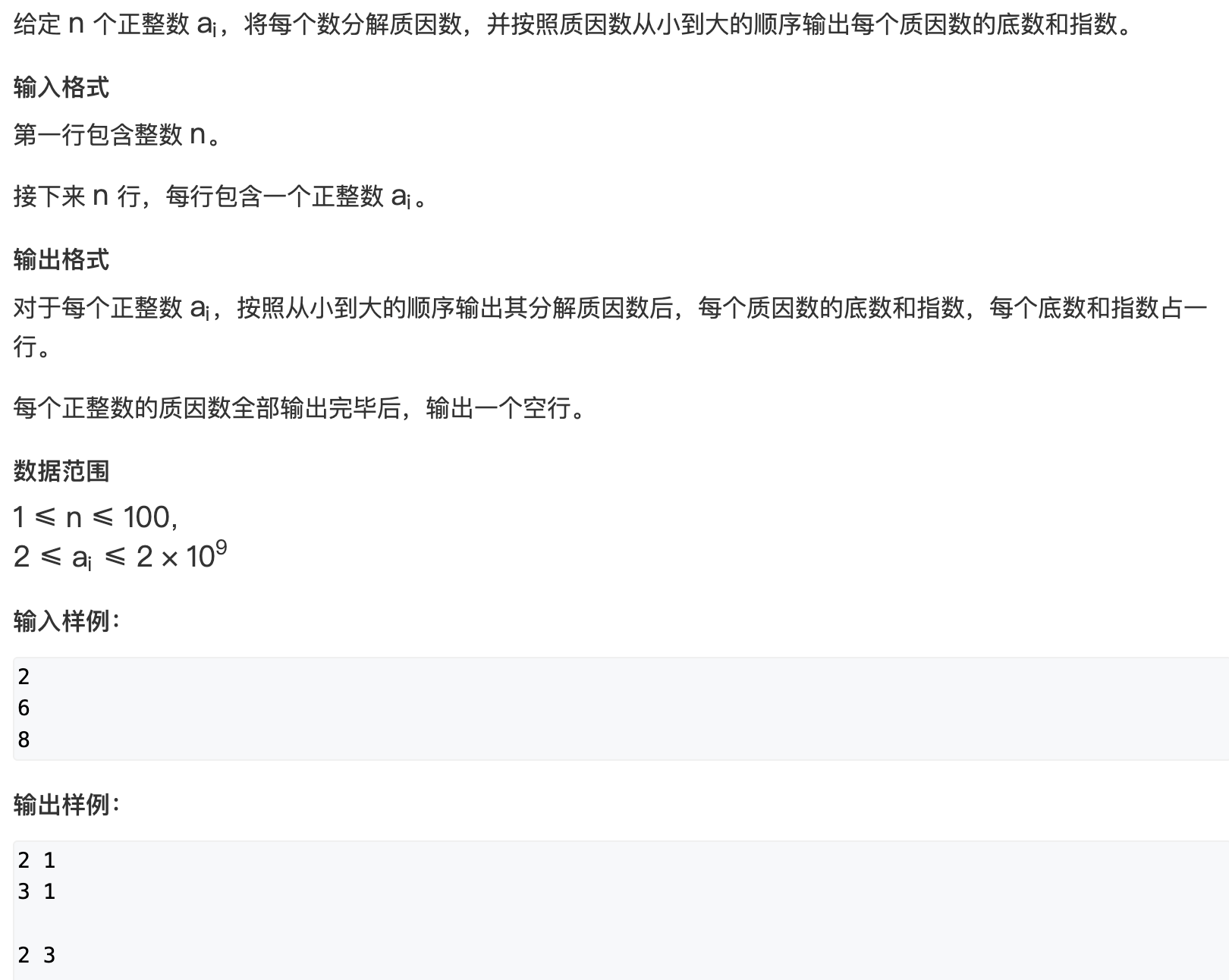
以为一个数的质因数只能从$2$开始, 从小到大枚举所有的因子, 尝试$n$的所有约数
算法时间复杂度$O(n)$

引理: $n$中最多只包含一个大于$\sqrt{n}$的质因子
证明: 假设存在两个大于$\sqrt{n}$的质因子$p$和$q$, 因为$p$和$q$都是$n$的质因子, 并且$p$和$q$互质, 因此$p\times q$也是$n$的质因子, 但是因为$p\times q>n$, 因此矛盾

大于$\sqrt{(}n)$的质因子指数只能是$1$, 因为如果指数$ > 1$,那么分解质因数的结果$ > n, 矛盾

因此$n$分解质因数后至多存在一个大于$\sqrt{n}$的质因子, 并且指数是$1$
优化后算法时间复杂度$O(\sqrt{n})$

#include <bits/stdc++.h>using namespace std;const int N = 110;int n;void solve() {int val;cin >> val;for (int i = 2; i <= val / i; ++i) {if (val % i == 0) {int cnt = 0;while (val % i == 0) {val /= i;cnt++;}if (cnt > 0) cout << i << ' ' << cnt << '\n';}}if (val > 1) cout << val << ' ' << 1 << '\n';cout << '\n';
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n;while (n--) solve();return 0;
}

线性筛法求质数

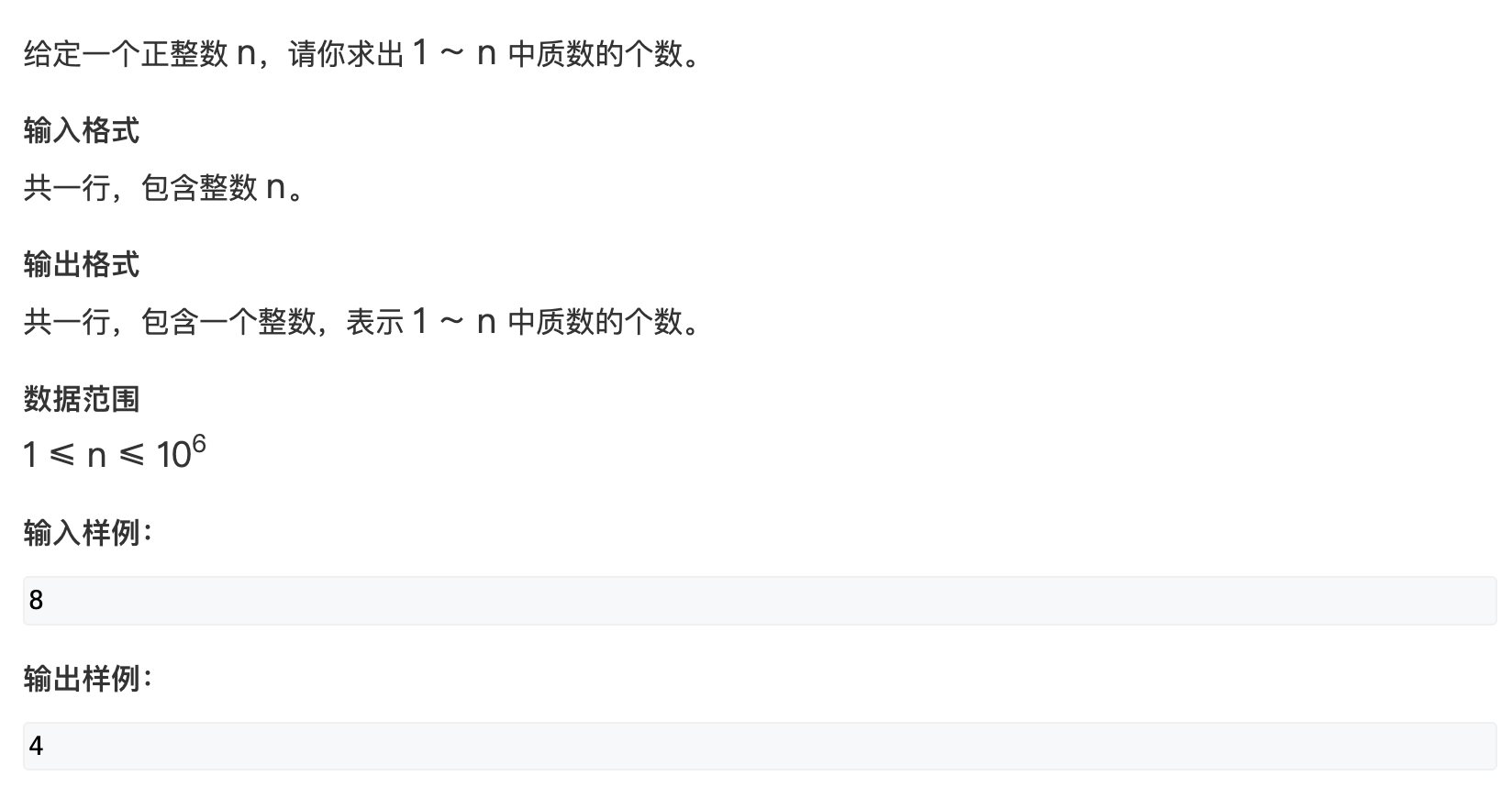
算法时间复杂度$O(n)$

#include <bits/stdc++.h>using namespace std;const int N = 1e6 + 10;int n;
bool st[N];
int primes[N], cnt = 0;void get_primes() {for (int i = 2; i <= n; ++i) {if (!st[i]) primes[cnt++] = i;for (int j = 0; i * primes[j] <= n; ++j) {st[i * primes[j]] = true;if (i % primes[j] == 0) break;}}
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n;get_primes();cout << cnt << '\n';return 0;
}

关于线性筛法的证明
因为每个合数只会被它的最小质因子筛掉, 因此算法是正确的并且是线性的
为什么只会被最小质因子筛掉, 分情况进行讨论

• 情况$1$, 因为第二维循环的质因子是从小到大枚举的, 当枚举到$i\mathrm{mod}{p}_j=0$的时候, 说明$p_j$是$i$的最小质因子, 因此$p_j$也是$i\times p_j$的最小质因子, 因此将$i\times p_j$筛掉
• 情况$2$, 因为第二维循环的质因子是从小到大枚举的, 当没有枚举到$i\mathrm{mod}{p}_j=0$的时候, $p_j$一定是$p_j\times i$的最小质因子, 也需要筛掉

综上, 只要是从小到大枚举质因子, 就需要筛掉, 直到当前的$p_j$已经是$i$的最小质因子了, 退出循环, 保证算法的线性时间复杂度

约数

试除法求约数

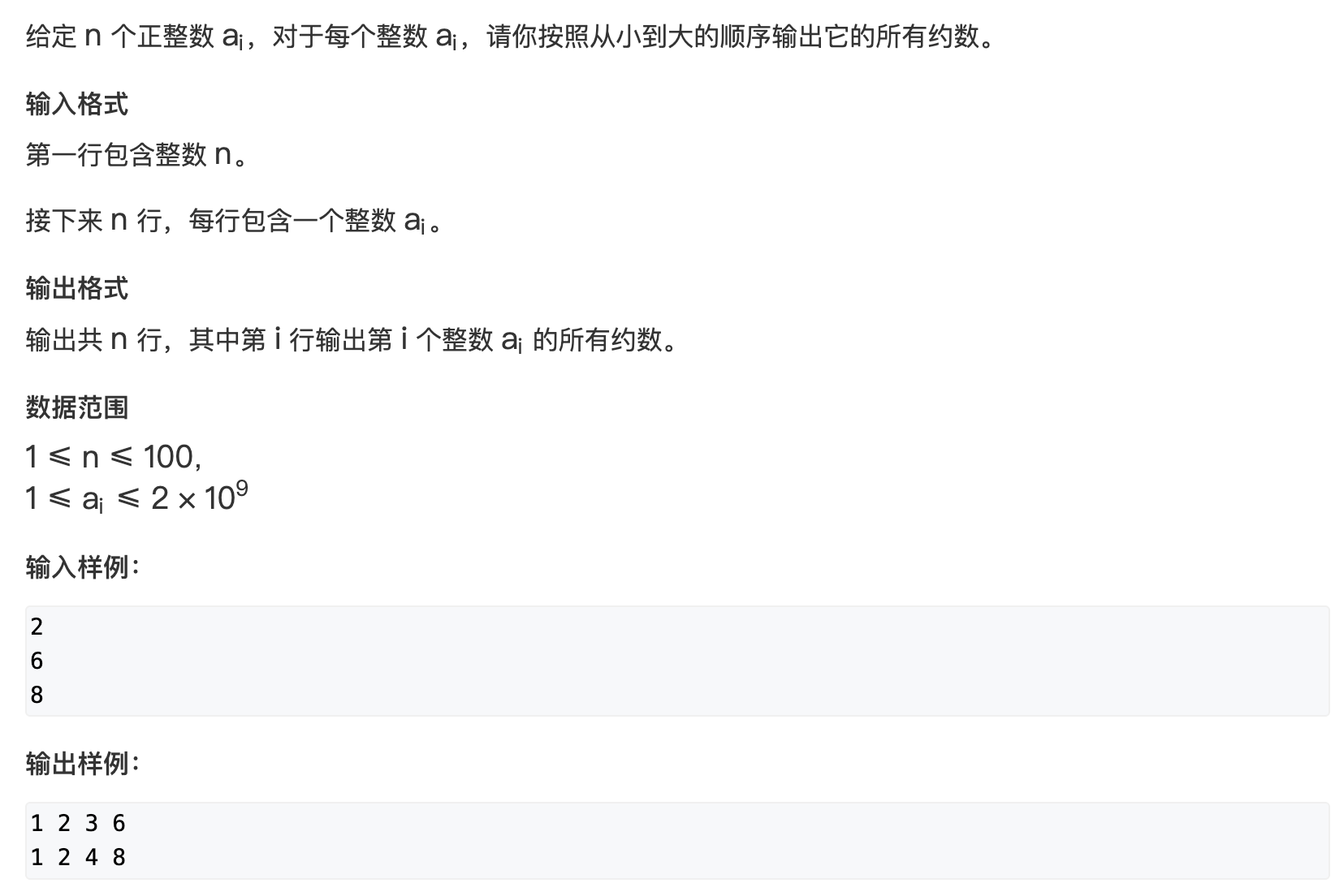
因为约数是成对出现的, 因此只需要枚举$d\le \sqrt{n}$的情况, 并且大于$\sqrt{n}$的约数只能是质数并且只能有一个, 计算约数后还需要去重排序, 算法时间复杂度$O(\sqrt{n}+n\log n)$

#include <bits/stdc++.h>using namespace std;const int N = 110;int n;void solve() {int val;vector<int> nums;cin >> val;for (int i = 1; i <= val / i; ++i) {if (val % i == 0) {nums.push_back(i);if (val / i != i) nums.push_back(val / i);}}sort(nums.begin(), nums.end());for (int d : nums) cout << d << ' ';cout << '\n';
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n;while (n--) solve();return 0;
}

约数个数

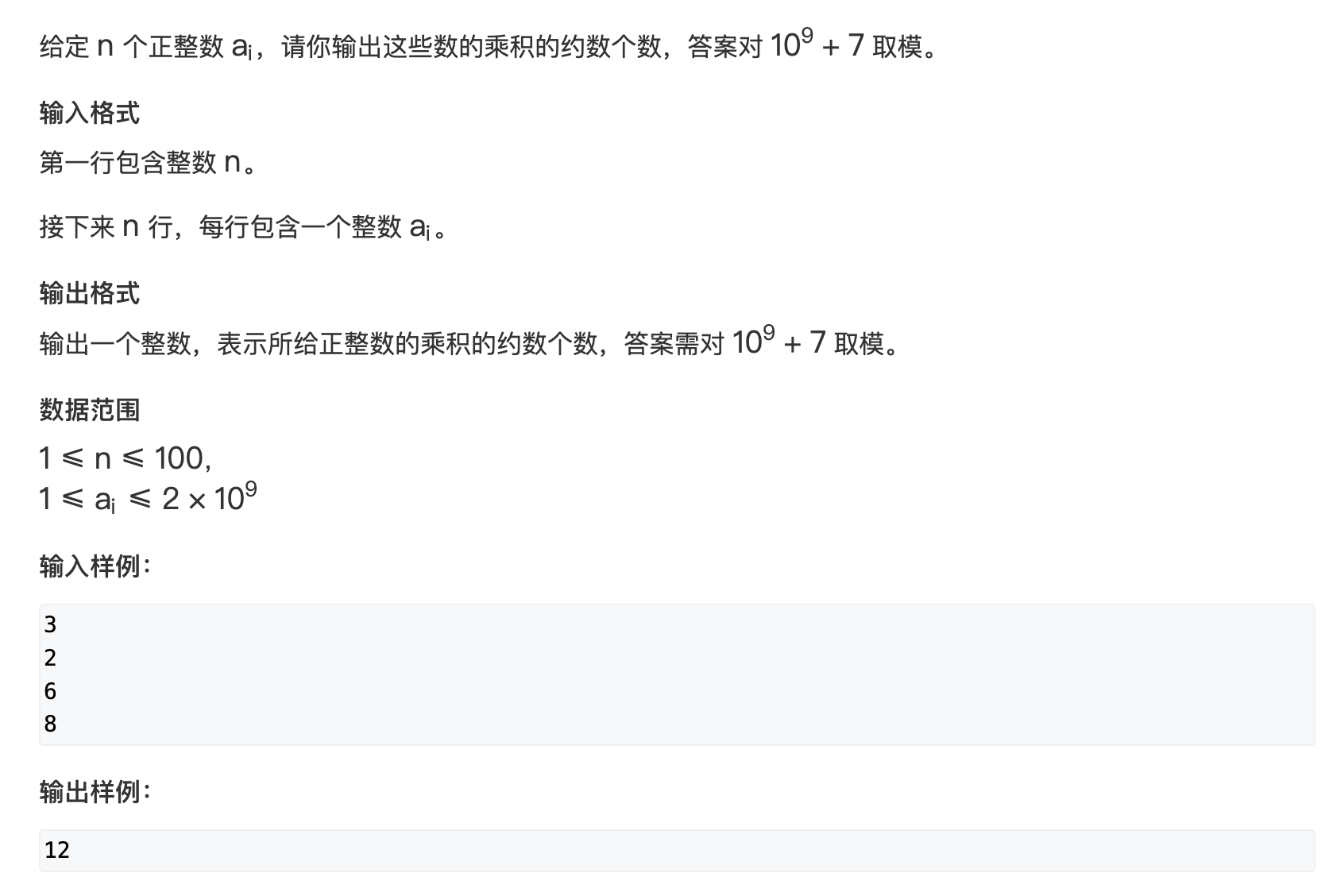
根据乘法原理, 约数个数$cnt=({\alpha }_0+1)\times ({\alpha }_1+1)\times ...\times ({\alpha }_k+1)$, 试除法分解质因数过程中求解指数的大小, 算法时间复杂度$O(\sqrt{n})$

#include <bits/stdc++.h>using namespace std;typedef long long LL;
const int MOD = 1e9 + 7;int n;
unordered_map<int, int> mp;void solve() {int val;cin >> val;for (int i = 2; i <= val / i; ++i) {while (val % i == 0) {val /= i;mp[i]++;}}if (val > 1) mp[val]++;
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n;while (n--) solve();LL res = 1;for (auto [x, y] : mp) res = res * (y + 1) % MOD;cout << res << '\n';return 0;
}

约数之和

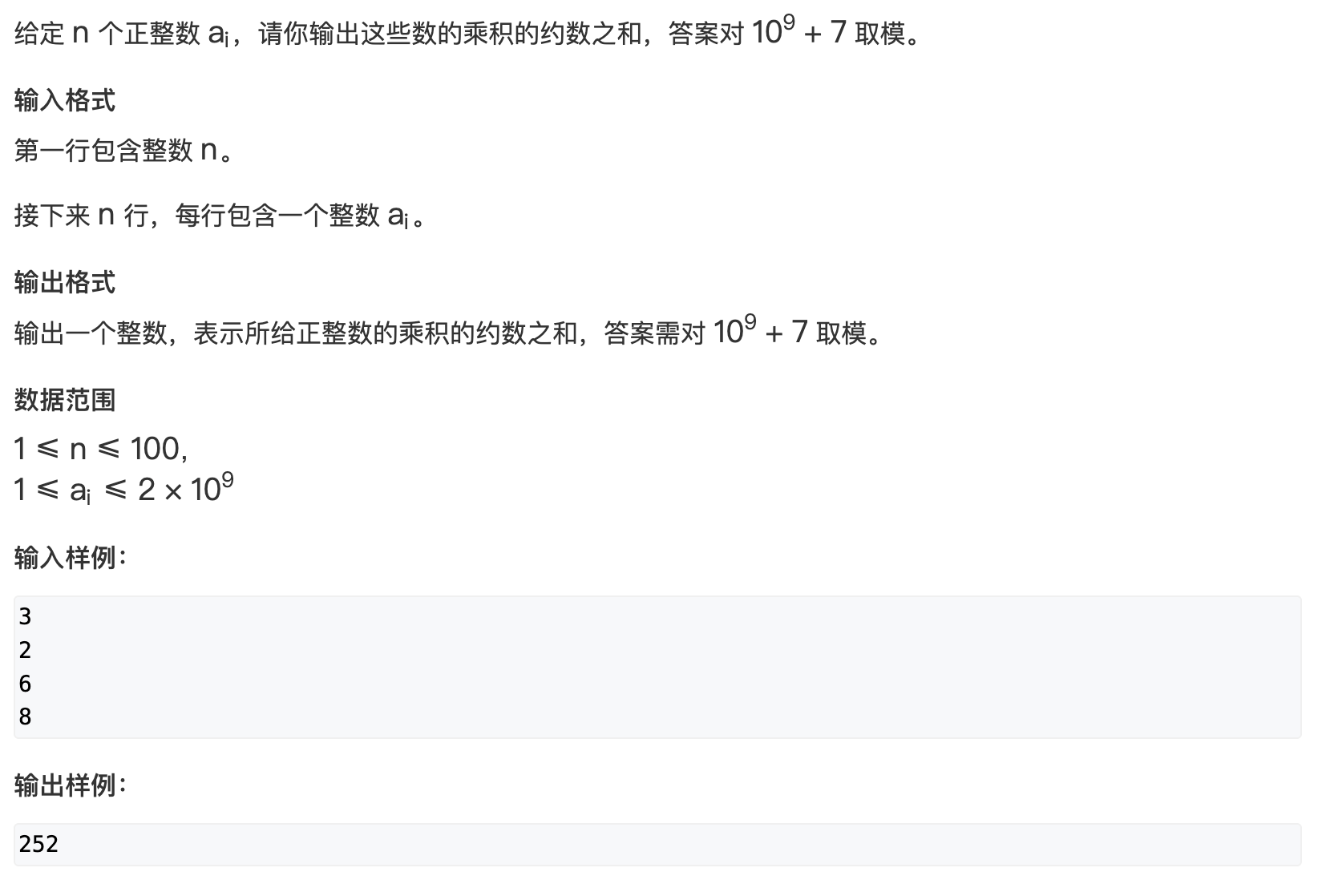
根据算术基本定理, 约数之和
$$sum=(p_1^0+p_1^1+...+p_1^{{\alpha }_1})(p_2^0+p_2^1+...+p_2^{{\alpha }_2})...(p_k^0+p_k^1+...+p_k^{{\alpha }_k})$$
依旧是分解质因数, 计算结果要取模, 算法时间复杂度$O(\sqrt{n})$

注意在计算$tmp$过程中要取模, 秦九韶算法求每一项, 内部的算法时间复杂度$O(n)$

总的算法时间复杂度$O(n\sqrt{n})$

#include <bits/stdc++.h>using namespace std;typedef long long LL;
const int MOD = 1e9 + 7;int n;
unordered_map<int, int> mp;void solve() {int val;cin >> val;for (int i = 2; i <= val / i; ++i) {while (val % i == 0) {val /= i;mp[i]++;}}if (val > 1) mp[val]++;
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n;while (n--) solve();LL res = 1;for (auto [x, y] : mp) {if (x != 0) {LL tmp = 1;// 秦九韶算法求p ^ 0 + p ^ 1 + ... + p ^ nwhile (y--) tmp = (tmp * x + 1) % MOD;res = res * tmp % MOD;}}cout << res << '\n';return 0;
}

最大公约数(gcd)算法

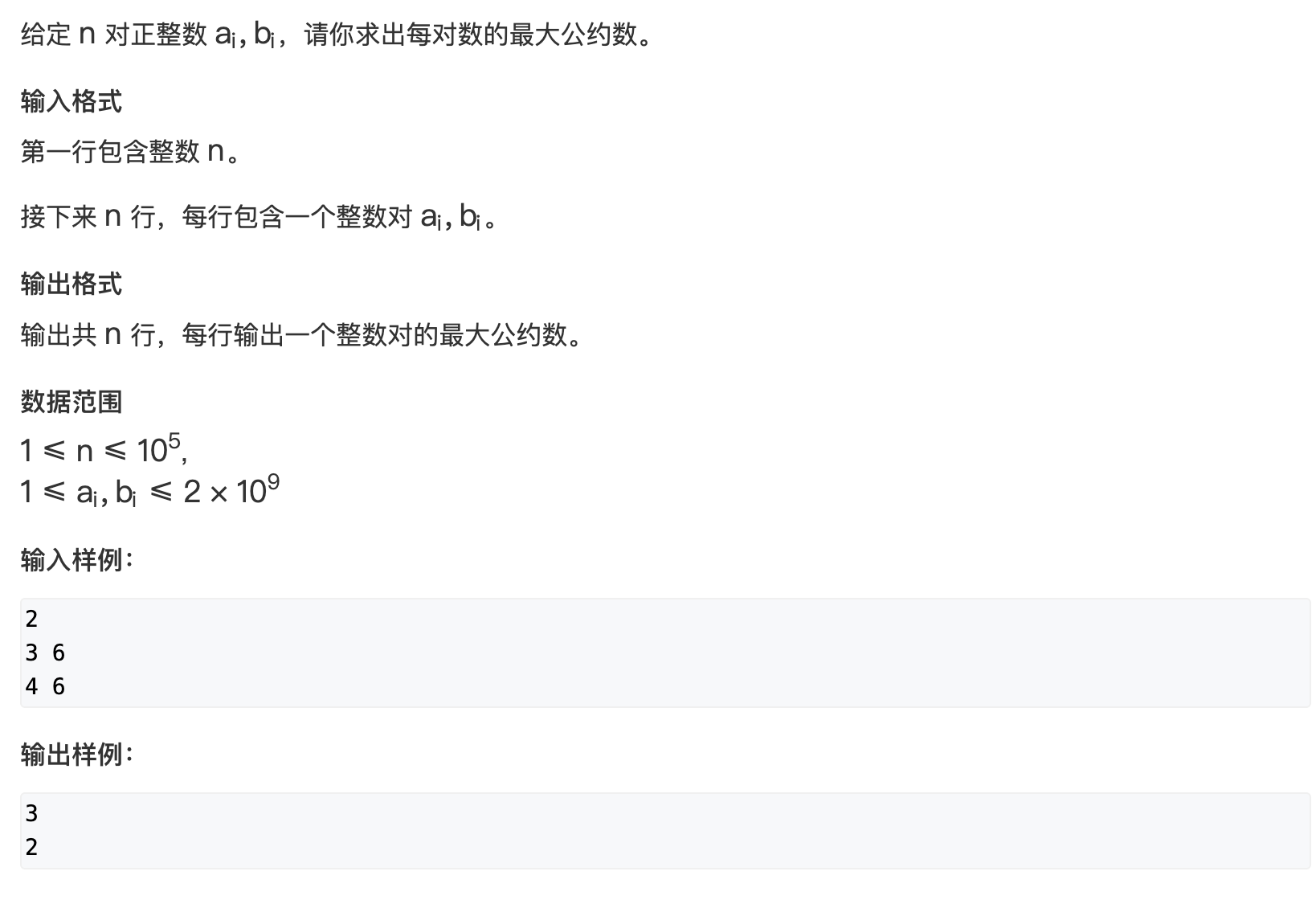
求最大公约数有两种算法, 欧几里得算法和更相减损法, 这里只讨论欧几里得算法
算法核心$\gcd (a,b)=\gcd (b,a\mathrm{mod}b)$

$$\begin{array}{rl}& \text{由 }d\mid a\text{，可设 }a=d\cdot m(m\in \mathbb{Z})\\ & \text{由 }d\mid b\text{，可设 }b=d\cdot n(n\in \mathbb{Z})\\ & \text{那么：}\\ & ax+by=(d\cdot m)x+(d\cdot n)y=d(mx+ny)\\ & \text{因为 }m,n,x,y\in \mathbb{Z}\text{，所以 }mx+ny\in \mathbb{Z}\\ & \text{因此 }d\mid (ax+by)\end{array}$$

算法时间复杂度$O(\log k)$

#include <bits/stdc++.h>using namespace std;int gcd(int a, int b) {return b ? gcd(b, a % b) : a;
}int main() {ios::sync_with_stdio(false);cin.tie(0);int n;cin >> n;while (n--) {int a, b;cin >> a >> b;cout << gcd(a, b) << '\n';}return 0;
}

Euler函数

容斥原理证明欧拉函数

将$n$分解质因数, 算法时间复杂度$O(\sqrt{n})$, 一个数的质因子最大数量是$\log n$, 因此求一个数字的欧拉函数算法时间复杂度$O(\log m\times \sqrt{m})$, 一共有$n$个数字, 算法时间复杂度$O(O(n\times \log m\times \sqrt{m}))$

注意为了避免超出$int$范围, 先做除法再做乘法

#include <bits/stdc++.h>using namespace std;int n;int solve() {int val;cin >> val;double res = val;for (int i = 2; i <= val / i; ++i) {if (val % i == 0) {res = res / i * (i - 1);while (val % i == 0) val /= i;}}if (val > 1) res = res / val * (val - 1);return res;
}int main() {ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);cin >> n;while (n--) {int res = solve();cout << res << '\n';}return 0;
}

线性筛法求欧拉函数

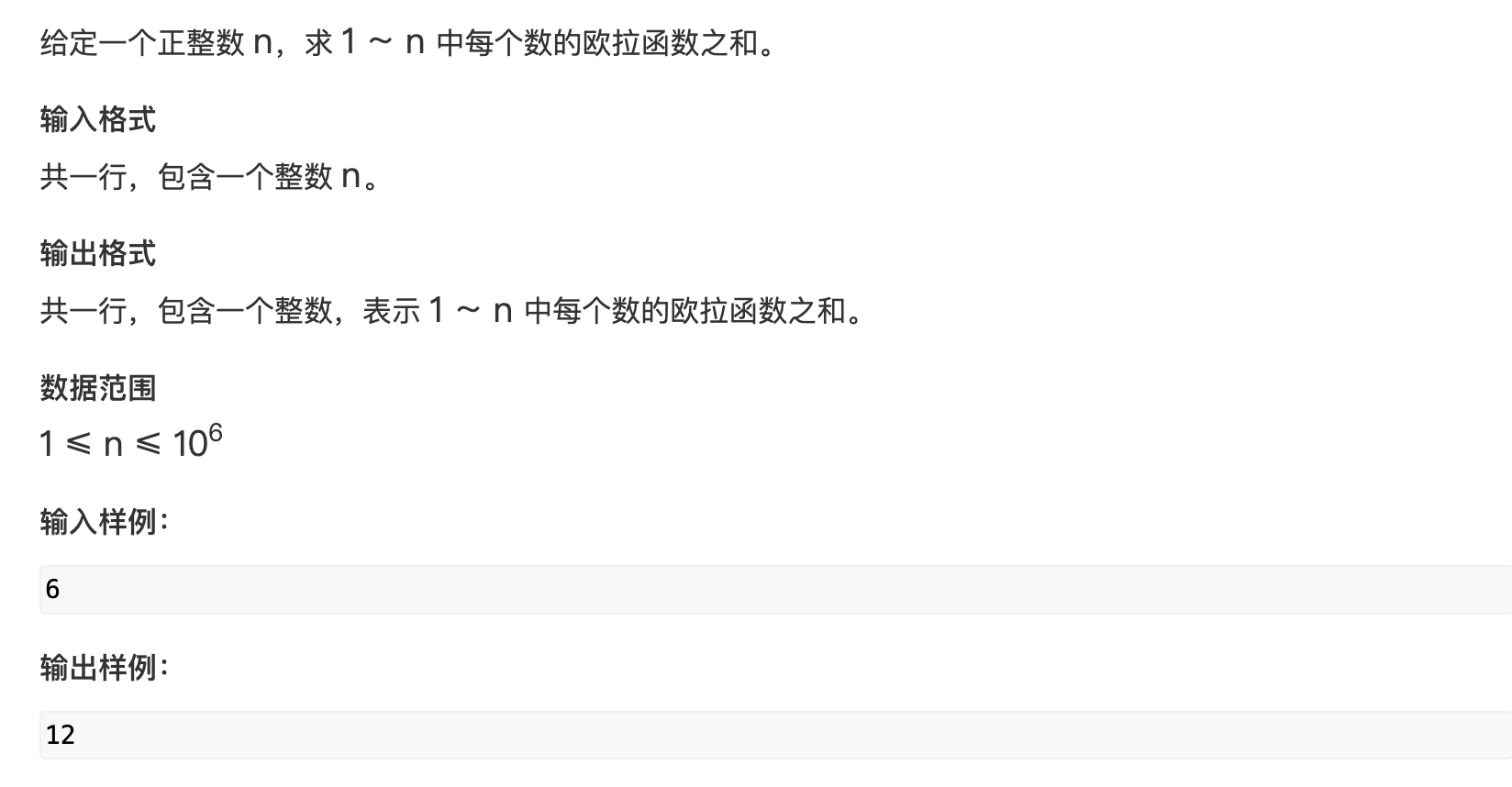
在线性筛质数基础上, 计算欧拉函数, 算法时间复杂度$O(n)$
下面是证明过程

如果当前数字是质数$i$, 那么$\varphi (i)=p-1$
如果当前数字$p$是$i$的最小质因子, $\varphi (i)=i\times k\times \frac{p-1}{p}$, 因此$\varphi (i\times j)=p\times \varphi (i)$
如果当前数字$p$比$i$的最小质因子小, 那么$p$是$i\times p$的最小质因子, 那么$\varphi (i\times j)=\varphi (i)\times p\times \frac{p-1}{p}$

#include <bits/stdc++.h>using namespace std;typedef long long LL;
const int N = 1e6 + 10;int n;
bool st[N];
int primes[N], phi[N], cnt;void init() {phi[1] = 1;for (int i = 2; i <= n; ++i) {if (!st[i]) {phi[i] = i - 1;primes[cnt++] = i;}for (int j = 0; primes[j] <= n / i; ++j) {st[i * primes[j]] = true;if (i % primes[j] == 0) {phi[i * primes[j]] = primes[j] * phi[i];break;}else phi[i * primes[j]] = phi[i] * (primes[j] - 1);}}
}int main() {ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);cin >> n;init();LL res = 0;for (int i = 1; i <= n; ++i) res += (LL) phi[i];cout << res << '\n';return 0;
}

快速幂, 龟速乘

快速幂算法

快速幂算法核心是反复平方法, 假设计算$a^b\mathrm{mod}M$, 可以预处理$a^{2^0},a^{2^1},a^{2^2},...$ , 然后将$b$展开为二进制数, 有$1$的地方说明要参与运算, 算法时间复杂度$O(\log b)$

#include <bits/stdc++.h>using namespace std;typedef long long LL;int pow(int a, int b, int p) {a = a % p;int res = 1;while (b) {if (b & 1) res = (LL) res * a % p;a = (LL) a * a % p;b >>= 1;}return res % p;
}int main() {ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int n;cin >> n;while (n--) {int a, b, p;cin >> a >> b >> p;cout << pow(a, b, p) << '\n';}return 0;
}

快速幂求逆元

乘法逆元的意思就是$\frac{a}{b}\equiv a\times x(\mathrm{mod}n)$, $x$就是乘法逆元, 也就是在$\mathrm{mod}n$的情况下, 可以将除法转化为乘法

欧拉定理: $a^{\varphi (n)}\equiv 1(\mathrm{mod}n)$, 其中$a$与$n$互质
欧拉定理的证明: 对于数字$n$的质因子如下$a_1,a_2,a_3,...,a_{\varphi (n)}$, 一共$\varphi (n)$个, 那么因为$a$与$n$会互质, 因此$a\cdot a_1,a\cdot a_2,...,a\cdot a_{\varphi (n)}$也与$n$互质, 但是因为$1$到$n$中与$n$互质的数的是确定的, 两段其实是一个集合, 也就是有$a_1\times a_2\times ...\times a_{\varphi (n)}=a\cdot a_1\times a\cdot a_2\times ...\times a\cdot a_{\varphi (n)}$
也就是等于$a^{\varphi (n)}\times k=k$, $k=a_1\times a_2\times ...\times a_{\varphi (n)}$, 因为每一个质因子都与$n$互质, 乘起来也与$n$互质, 因此有$a^{\varphi (n)}\equiv 1(\mathrm{mod}n)$, 证毕

费马小定理: $a^{p-1}\equiv 1(\mathrm{mod}p)$

根据费马小定理, 计算乘法逆元的过程可以表示为$a\cdot a^{p-2}\equiv 1(\mathrm{mod}n)$, $a^{p-2}$就是$a$在$\mathrm{mod}p$下的乘法逆元, 其中$a$与$n$互质
利用快速幂计算$a^{p-2}$, 时间复杂度$O(\log b)$

#include <bits/stdc++.h>using namespace std;typedef long long LL;LL pow(int a, int b, int p) {LL res = 1 % p;a %= p;b %= p;while (b) {if (b & 1) res = (LL) res * a % p;b >>= 1;a = (LL) a * a % p;}return res;
}int main() {ios::sync_with_stdio(false);cin.tie(0);int n;cin >> n;while (n--) {int a, p;cin >> a >> p;if (a % p == 0) {cout << "impossible" << '\n';continue;}LL res = pow(a, p - 2, p);cout << res << '\n';}return 0;
}

龟速乘算法

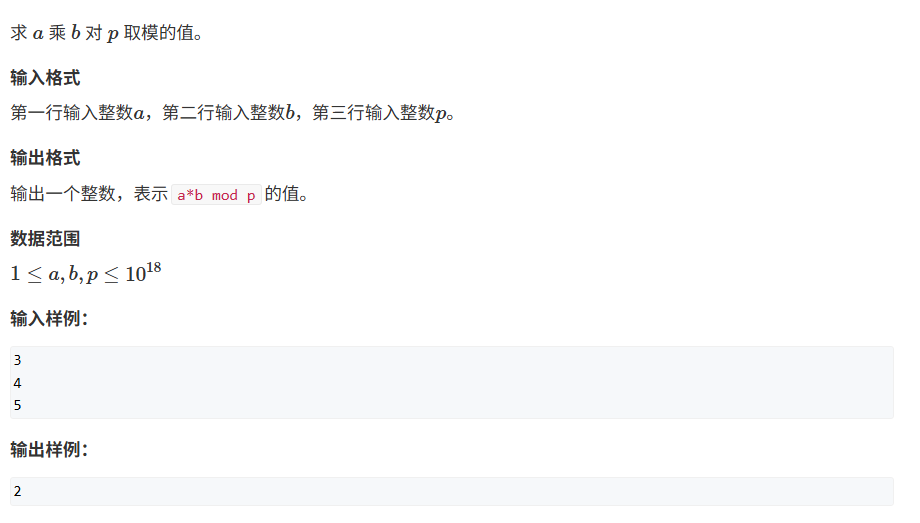
将$b$拆分为二进制数, 预处理
$a\times 2^0,a\times 2^1,a\times 2^2,a\times 2^3,\dots$
然后利用二进制拼凑的思想, 凑出$b$
正常的计算乘法时间复杂度是$O(1)$, 但是该算法的时间复杂度是$O(\log b)$

#include <bits/stdc++.h>using namespace std;typedef long long LL;LL slow_mul(LL a, LL b, LL p) {LL res = 0;while (b) {if (b & 1) res = (res + a) % p;b >>= 1;a = (a + a) % p;}return res;
}int main() {ios::sync_with_stdio(false);cin.tie(0);LL a, b, p;cin >> a >> b >> p;cout << slow_mul(a, b, p) << '\n';return 0;
}

扩展欧几里得算法

裴蜀定理: