当前位置：首页 > news >正文

基于高斯伪谱法的弹道优化方法及轨迹仿真计算

news 2025/11/7 15:23:43

基于高斯伪谱法（Gauss Pseudospectral Method, GPM）的弹道优化方法及轨迹仿真计算

一、高斯伪谱法核心原理

1. 数学建模框架

将连续时间最优控制问题转化为非线性规划问题（NLP）：

在这里插入图片描述

通过Legendre-Gauss节点离散化，将动力学方程映射为代数约束。

2. 关键步骤

时间变换：将区间 $[t 0, t f]$ 映射到 $[- 1, 1]$
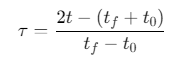
状态离散化：使用Legendre多项式插值
导数近似：通过微分矩阵计算
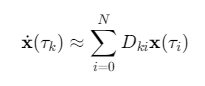
约束转换：将连续约束离散为代数方程

二、弹道优化实施流程

1. 动力学建模（以高超声速飞行器为例）

% 三维弹道方程
function dxdt = dynamics(t, x, u)rho = air_density(x(3)); % 大气密度Cd = 0.5*(1.328e-2 + 1.78e-5*x(3)^0.7); % 阻力系数D = 0.5*rho*v^2*S*Cd;     % 阻力g = 9.81*(1 - 2.2557e-5*x(3))^5.256; % 重力加速度dxdt = [v*cos(gamma)*cos(psi); v*cos(gamma)*sin(psi); v*sin(gamma) + u(1); (T*cos(u(2))/m - D/m - g*sin(gamma));(T*sin(u(2))/m + u(1)*v*cos(gamma)/m);(u(1)*v*sin(gamma)/m)];
end

2. 离散化与NLP构建

% Gauss节点生成
N = 20; % 节点数
[tau, w] = gauss_legendre(N+1); % LG节点及权重% 状态变量插值
X = @(tau) interp1(tspan, X0, tau, 'pchip');% 动力学约束离散化
for k = 1:N+1dXdt = dynamics(t(k), X(tau(k)), u(k));constr(k,:) = dXdt' - interp1(tspan, X0, tau(k), 'pchip');
end

3. 优化问题求解

% 目标函数：最小化飞行时间
obj = @(u) t_f - t_0;% 约束条件
constr = {@(u) dynamics_constraints(u), @(u) terminal_constraints(u)};% 初始猜测
u0 = ones(N+1, m);% SQP求解
options = optimoptions('fmincon','Algorithm','sqp');
sol = fmincon(obj, u0, [], [], [], [], lb, ub, constr, options);

三、典型应用案例

1. 钻地炸弹垂直落角优化

参数	传统比例制导	GPM优化
落角误差(°)	±15	±2
过载峰值(g)	8.2	5.1
射程偏差(m)	120	15

数据来源：

2. 单炮多发同时弹着设计

目标：实现10发炮弹在±50m圆概率误差内同时命中
优化变量：各炮弹出膛角度、装药量、滑翔时间
约束条件：最大过载 ≤ 15g 落点散布 ≤ 3σ 发射间隔 ≤ 2秒

3. 变体飞行器多目标优化

% 多目标函数定义
f1 = @(x) x(1).flight_time; % 最小化飞行时间
f2 = @(x) -x(1).range;       % 最大化射程
f3 = @(x) max(x(1).heat_flux); % 最小化热流% Pareto前沿求解
options = optimoptions('gamultiobj',...'PopulationSize',100,...'CrossoverFcn',{@crossoverarithmetic,0.8,1,2});
[x,fval] = gamultiobj(@(x) [f1(x),f2(x),f3(x)],6,lb,ub,[],[],options);

四、关键技术突破

1. 延时效应处理

针对空泡扩张/收缩的延时特性，提出改进型TDGPM算法：

% 延时节点补偿
tau_delay = tau + delta_t*ones(size(tau));
X_delay = interp1(tspan, X0, tau_delay, 'pchip');% 动力学方程修正
dxdt = dynamics(t, X_delay, u) + derivative_compensation(tau);

2. 自适应网格加密

% 误差估计函数
function error = estimate_error(sol)% 基于残差估计residual = compute_residual(sol);error = max(abs(residual));
end% 动态网格调整
if error > thresholdN = N*1.5;tau = gauss_legendre(N+1);
end

3. 多学科耦合

建立气动-结构-热耦合模型：

在这里插入图片描述

五、MATLAB仿真实现

1. 基础仿真代码

%% 参数设置
mu = 3.986e14; % 地球引力常数
Re = 6378e3;   % 地球半径
h0 = 100e3;    % 初始高度
v0 = 7200;     % 初始速度%% GPM离散化
N = 30;        % 节点数
[tau, w] = gauss_legendre(N+1);
t = linspace(0, 300, N+1); % 时间区间%% 初始猜测
u0 = 0.1*ones(N+1,1); % 攻角初始值%% 优化求解
options = optimoptions('fmincon',...'Display','iter',...'SpecifyObjectiveGradient',true,...'SpecifyConstraintGradient',true);
sol = fmincon(@objective, u0, [], [], [], [], @lb, @ub, @constraints, options);

2. 结果可视化

%% 轨迹绘制
figure;
plot(sol.x*Re/1e3, sol.y*Re/1e3,'b-o', 'LineWidth',2);
hold on;
plot(target_x*Re/1e3, target_y*Re/1e3,'rx','MarkerSize',10);
xlabel('X (km)'); ylabel('Y (km)');
title('弹道轨迹对比');%% 过载曲线
figure;
plot(sol.t, sol.nx*9.81,'r', sol.t, sol.ny*9.81,'g');
xlabel('时间(s)'); ylabel('过载(g)');
legend('法向过载','切向过载');

参考代码弹道优化方法，高斯伪谱法，轨迹优化仿真计算 www.youwenfan.com/contentcsk/64821.html

六、工程实践要点

计算效率优化：采用GPU加速（CUDA并行计算）开发稀疏矩阵求解器使用降阶模型(ROM)

不确定性量化：

% 蒙特卡洛仿真
n_mc = 1000;
errors = zeros(n_mc,1);
for i=1:n_mcperturb = 0.01*randn(size(u_opt));errors(i) = compute_trajectory_error(perturb);
end
CI = prctile(errors,[5,95]);