计算机图形学·10 表示（Representation）

本文是记录专业课“计算机图形学”的部分笔记，参考教材为Angel的第八版交互式计算机图形学——基于WebGL 2.0的自顶向下方法。

1、一组向量v1, v2 ,…, vn称为线性无关的，是指α1v1+α2v2+.. αnvn=0 当且仅当 α1=α2=…=0。如果一组向量线性无关，就不能把其中一个向量表示成其它向量的线性组合；反之，如果一组
向量线性相关，则其中至少有一个向量可以表示为其它向量的线性组合。
2、在某个向量空间中，最大的线性无关向量组的元素个数是固定的，这个数就称为该空间的维数。在n维空间中，任意一组n个线性无关的向量都能构成空间的基（basis）。给定空间的一组基v1, v2,…, vn，空间中每一个向量v都可以表示为v = α1v1+ α2v2 +….+ αvn其中参数{αi}是唯一的。
3、到现在为止我们只是讨论几何对象，而没有使用任何参考系统，例如坐标系、标架。我们需要一个参考系统把点和对象与物理世界联系在一起（如World coordinates世界坐标系、Camera coordinates照相机坐标系）。
4、先考虑坐标系（Coordinate Systems），注意下图的表示是相对一个特定的基而言的。例如在OpenGL中刚开始是相对于世界坐标系表示向量的，稍后要把这个表示变换到照相机坐标系，在这里几何对象没有变化，”表示“（Representation）变化了。此外需要注意，向量没有固定位置可言。

5、我们发现，坐标系是不足于表示点的，如果要在仿射空间中考虑问题，可以在基向量组中增加一个点（原点），从而构成一个标架（frame）。标架是由(P0, v1,v2, v3)的确定的（如三维形式），在标架中，每个向量可以表示为v=a1v1+ a2v2 +….+anvn（n维形式）、每个点可以表示为P = P0 + b1v1+ b2v2 +….+bnvn 。换个形式， 点 - 点 = 矢量依然成立：P - P0 = = b1v1+ b2v2 +….+bnvn。
6、不过在标架中，点和向量看起来具有相似的矩阵表示，比如三维形式的点P=[β1 β2 β3]、向量v=[α1 α2 α3]。我们定义：

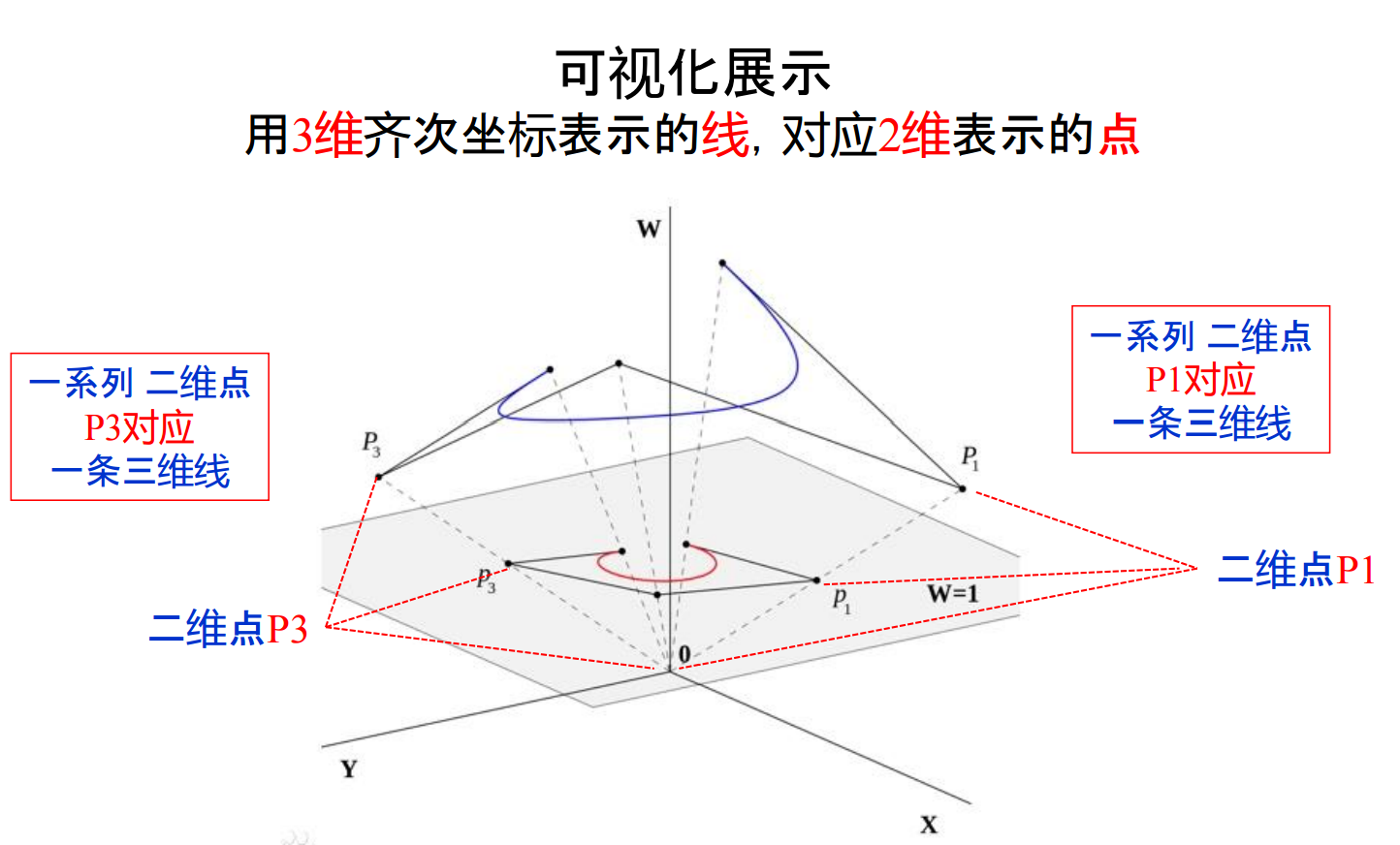
于是我们得到了三维点齐次坐标的一般形式为p =[x’ y’ z’ w] T =[wx wy wz w] T =[x y z 1] T，这里的w是哑元参数，本例中为1，实现从四维线降维到三维点。我们可以通过下述方法给出三维点（当w ≠ 0）：x<-x’/w、y<-y’/w、z<-z’/w。特别的，当w=0，xyz无穷大的点，点→矢量，位置→方向，表示对应的是一个向量，表示方向、无穷远。可以这么理解：齐次坐标表示中，把四维空间中过原点的一条直线对应于三维空间中的一个点，如图。

7、齐次坐标是所有计算机图形系统的关键，所有标准变换（旋转、平移、放缩）都可以应用4×4阶矩阵的乘法实现，硬件流水线体系也可以应用四维表示。比如，对于正交投影，可以通过w = 0保证表示向量，w= 1保证表示点 （隐含，观察投影方向，没有具体位置，无穷远）。而透视除法需要进行特别的处理（非线性，非均匀缩放） （隐含，存在一个观察投影中心点，有限距离位置）
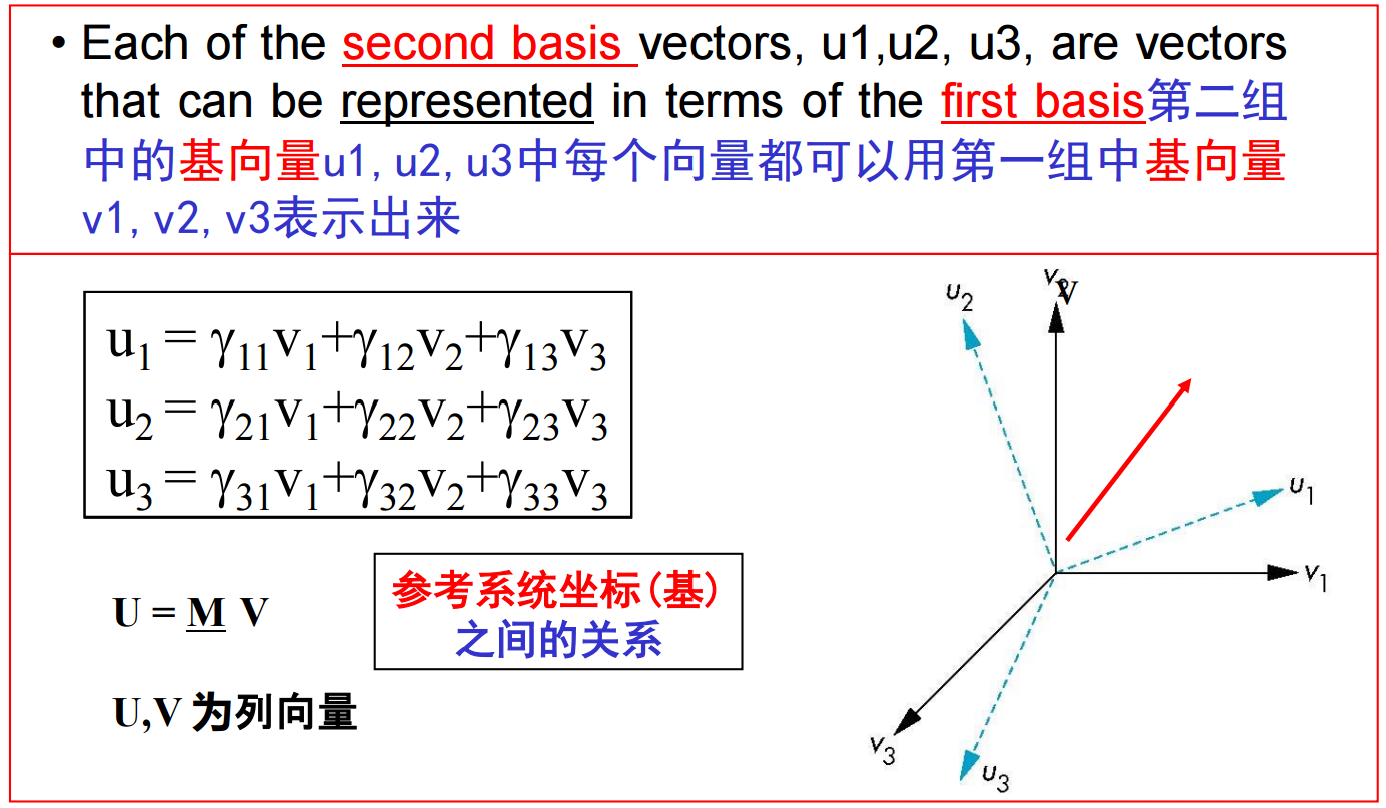
8、考虑同一个向量相对于两个不同基的表示分别是a=α1v1+ α2v2 +α3v3 = [α1 α2 α3]  [v1 v2 v3] T，b=β1u1+ β2u2 +β3u3 = [β1 β2 β3]  [u1 u2 u3] ，则：


当然，可以同时对表示点与向量的齐次坐标进行类似的操作(P0, v1, v2, v3) (Q0, u1, u2, u3)：

一样的，表示的变换（点或者向量）还是a=MT b，b=（MT）^(-1)a，这里的矩阵M是4×4阶，是用齐次坐标定义一个仿射变换。
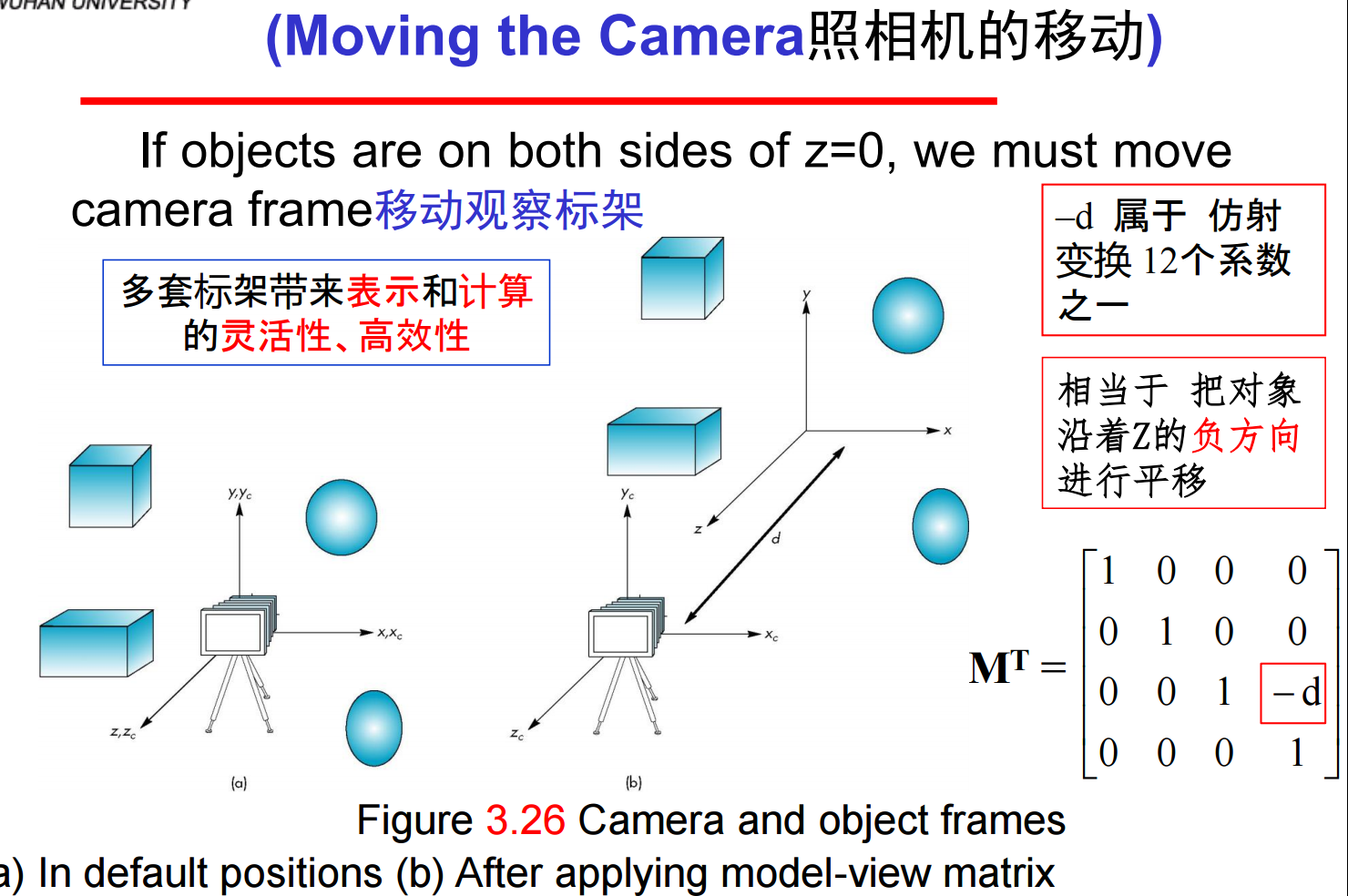
9、事实上，每个线性变换等价于一次标架改变，所有的仿射变换保持共线性（保直线straightness 、保比例parallelness ，不保角度，符合自然物理世界的视觉观察客观规律）。然而，一个仿射变换只具有12个自由度，因为所有仿射变换只是由4×4阶矩阵定义的所有线性变换的子集，所以矩阵的16个元素中有四个元素是固定的（M的最右列或M T的最下行为0001）。后续我们将看到这12个元素如何形成仿射变换。
10、当提及表示（Representation）的时候，所指的是由n个标量构成的有序数组，标架的改变由一个4×4阶矩阵定义。在OpenGL中开始的基本标架是世界标架，最终我们是在照相机标架中表示几何体，这是用模型-视图矩阵进行变换的，初始状态时这两个标架是相同的 （M=I，相当于没有运算）。