当前位置： 首页 > news >正文

C++高级数据结构：并查表

news 2025/11/7 12:06:43

        在前面的内容中我们已经接触到了一些C++的高级数据结构，如AVL数、红黑树、哈希表等，但是实际上C++常用的数据结构不仅这些，接下来我们将深入图等高级的数据结构。不过在讲解图之前我们需要了解前置的数据结构：并查表。来方便我们学习图

        相关代码已经上传至作者的个人gitee：楼田莉子/CPP代码学习喜欢请点个赞谢谢

目录

并查集原理

并查集的实现

        简单版本的实现

        完整版实现

并查集的应用

        省份数量

        等式方程的可满足性

并查集原理

        在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find set)。

        下面举例说明：

        某公司今年校招全国总共招生10人，西安招4人，成都招3人，武汉招3人，10个人来自不同的学校，起先互不相识，每个学生都是一个独立的小团体，现给这些学生进行编号：{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; 给以下数组用来存储该小集体，数组中的数字代表：该小集体中具有成员的个数。

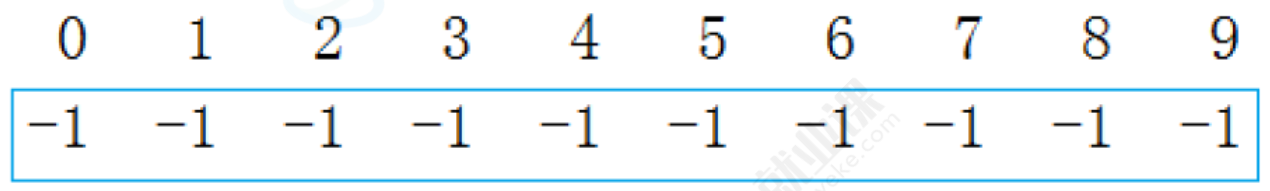
        与堆类似，用数组下标表示树的关系。

        初始状态用-1表示一个集合

        毕业后，学生们要去公司上班，每个地方的学生自发组织成小分队一起上路，于是：

        西安学生小分队s1={0,6,7,8}，成都学生小分队s2={1,4,9}，武汉学生小分队s3={2,3,5}就相互认识了，10个人形成了三个小团体。假设右三个群主0,1,2担任队长，负责大家的出行。我们可以用数的方式表示

        如果0跟6是朋友，那么把6所对应的-1加到0上，6号位变为0，0号位变为-2。这就是双亲表示法。

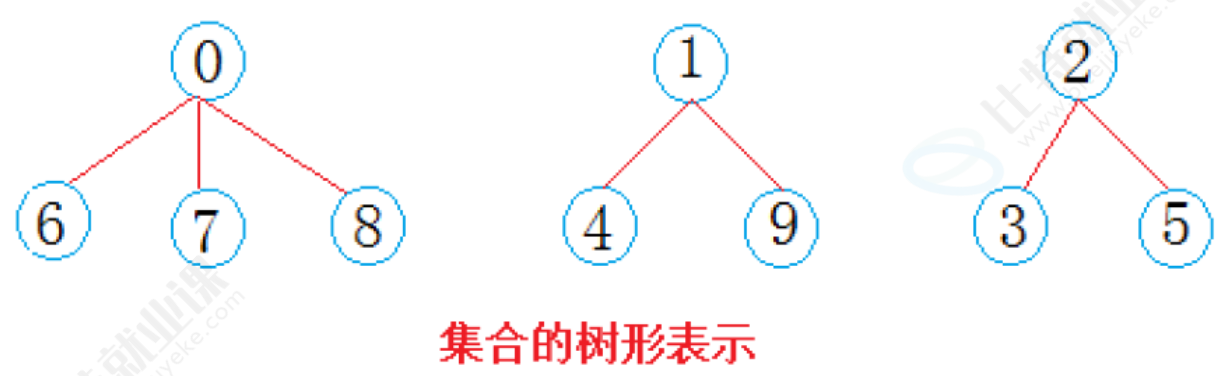
        特点：

        1、如果一个下标位置的值是负数，那它就是根。

        2、如果一个下标位置的值是正数，那么它就是双亲的下标。

        一趟火车之旅后，每个小分队成员就互相熟悉，称为了一个朋友圈。

        

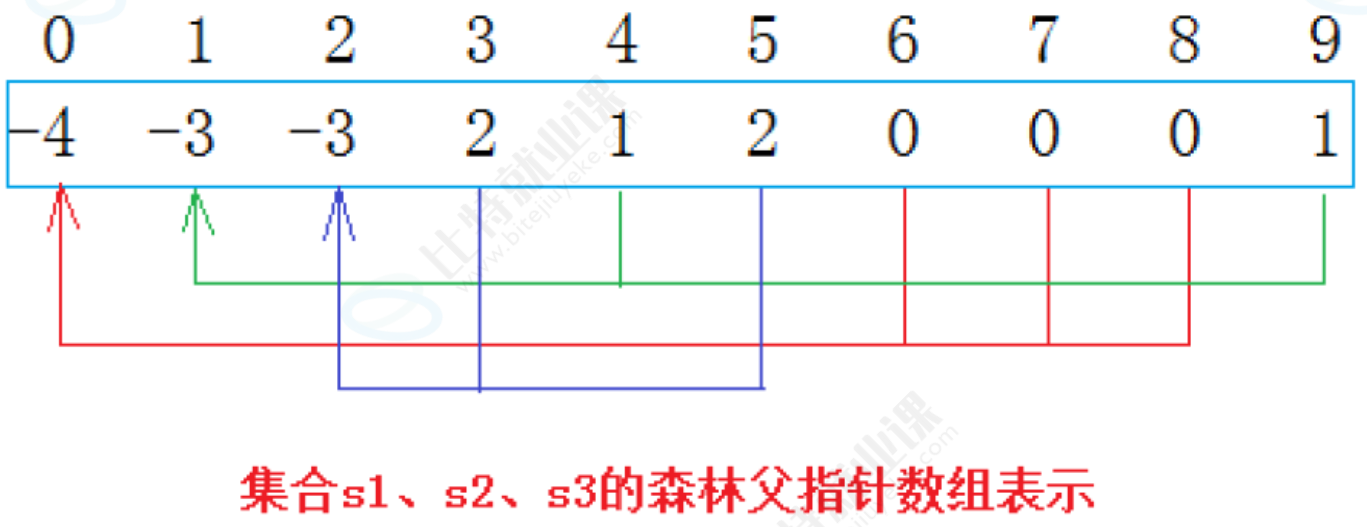
        从上图可以看出：编号6,7,8同学属于0号小分队，该小分队中有4人(包含队长0)；编号为4和9的同学属于1号小分队，该小分队有3人(包含队长1)，编号为3和5的同学属于2号小分队，该小分队有3个人(包含队长1)。

        仔细观察数组中内融化，可以得出以下结论：

        1. 数组的下标对应集合中元素的编号

        2. 数组中如果为负数，负号代表根，数字代表该集合中元素个数

        3. 数组中如果为非负数，代表该元素双亲在数组中的下标

        在公司工作一段时间后，西安小分队中8号同学与成都小分队1号同学奇迹般的走到了一起，两个小圈子的学生相互介绍，最后成为了一个小圈子：

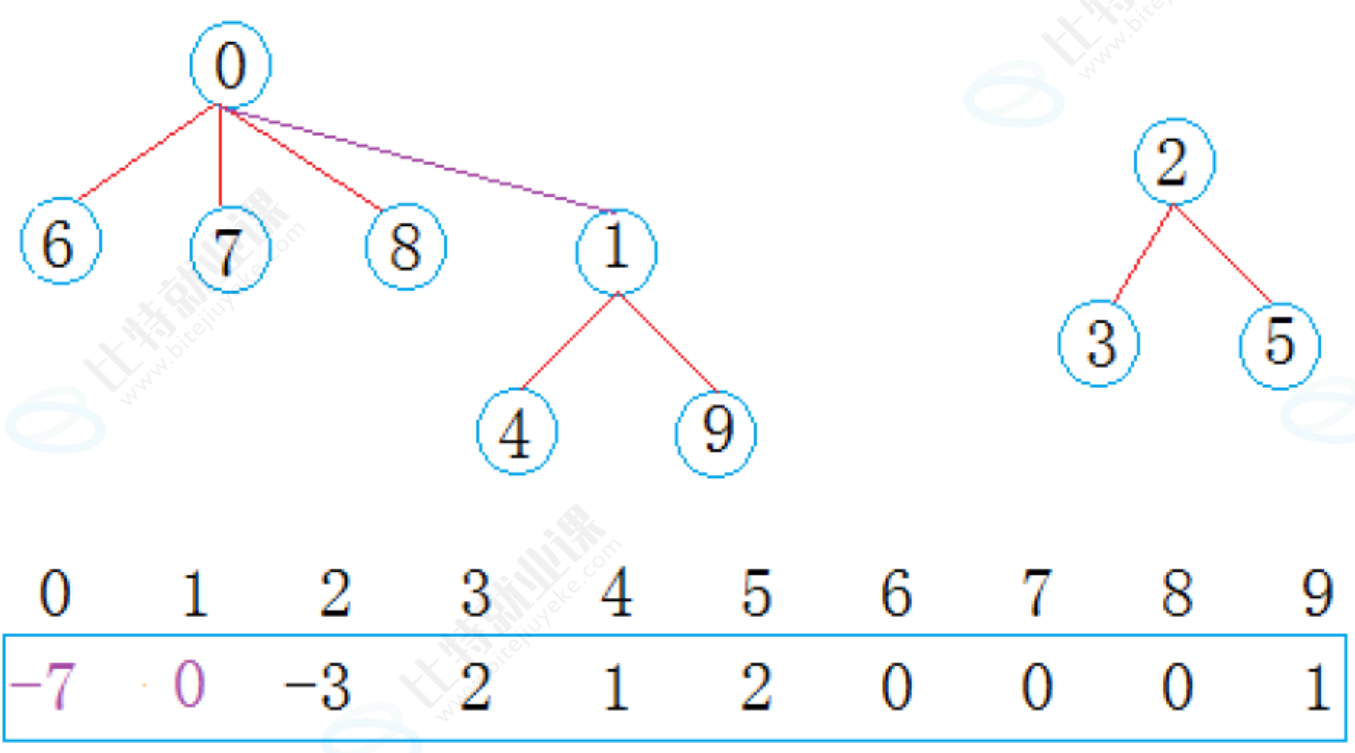
        现在0集合有7个人，2集合有3个人，总共两个朋友圈。通过以上例子可知，并查集一般可以解决一下问题：

        1. 查找元素属于哪个集合

        沿着数组表示树形关系以上一直找到根(即：树中中元素为负数的位置)

        2. 查看两个元素是否属于同一个集合

        沿着数组表示的树形关系往上一直找到树的根，如果根相同表明在同一个集合，否则不在

        3. 将两个集合归并成一个集合

        将两个集合中的元素合并

        将一个集合名称改成另一个集合的名称

        4. 集合的个数

        遍历数组，数组中元素为负数的个数即为集合的个数。

并查集的实现

        简单版本的实现

//UnionFindSet2.h
#pragma once
#include <vector>
#include <algorithm>
using std::vector;
using std::swap;
namespace DSU
{class UnionFindSet{public:// 初始时，将数组中元素全部设置为1UnionFindSet(size_t size): _ufs(size, -1){}// 给一个元素的编号，找到该元素所在集合的名称int FindRoot(int index){// 如果数组中存储的是负数，找到，否则一直继续while (_ufs[index] >= 0){index = _ufs[index];}return index;}// 合并两个集合bool Union(int x1, int x2){int root1 = FindRoot(x1);int root2 = FindRoot(x2);// x1已经与x2在同一个集合if (root1 == root2)return false;//小的合并大的if (root1 > root2){swap(root1, root2);}// 将两个集合中元素合并_ufs[root1] += _ufs[root2];// 将其中一个集合名称改变成另外一个_ufs[root2] = root1;return true;}//两个集合是否相等bool Inset(int root1, int root2){return FindRoot(root1) == FindRoot(root2);}// 数组中负数的个数，即为集合的个数size_t Count()const{size_t count = 0;for (auto e : _ufs){if (e < 0)++count;}return count;}private:vector<int> _ufs;};
}

        完整版实现

//UnionFindSet.h
#pragma once
#include <vector>
#include <map>
#include <string>
#include <unordered_map>
#include <unordered_set>
#include <iostream>
#include <initializer_list>
using std::vector;
using std::map;
using std::string;
using std::unordered_map;
using std::unordered_set;
using std::initializer_list;//并查集的数据结构实现
namespace DSU
{template<class T>class UnionFindSet{public:// 默认构造函数UnionFindSet() = default;// 列表初始化构造函数UnionFindSet(std::initializer_list<T> initList){size_t i = 0;for (const T& element : initList){_data.push_back(element);_indexMap[element] = i;_parent.push_back(i);_size.push_back(1);++i;}_setCount = initList.size();}// 通过数组初始化UnionFindSet(const T* a, size_t n){for (size_t i = 0; i < n; ++i){_data.push_back(a[i]);_indexMap[a[i]] = i;_parent.push_back(i);_size.push_back(1);}_setCount = n;}// 通过vector初始化UnionFindSet(const vector<T>& data){for (size_t i = 0; i < data.size(); ++i){_data.push_back(data[i]);_indexMap[data[i]] = i;_parent.push_back(i);_size.push_back(1);}_setCount = data.size();}// 添加新元素void AddElement(const T& element){if (_indexMap.find(element) != _indexMap.end())return;size_t newIndex = _data.size();_data.push_back(element);_indexMap[element] = newIndex;_parent.push_back(newIndex);_size.push_back(1);_setCount++;}// 批量添加元素void AddElements(std::initializer_list<T> elements){for (const T& element : elements){AddElement(element);}}// 查找元素所在集合的根节点索引int FindRoot(int index){// 路径压缩if (_parent[index] != index){_parent[index] = FindRoot(_parent[index]);}return _parent[index];}// 查找元素所在集合的根节点索引（通过元素值）int FindRoot(const T& element){auto it = _indexMap.find(element);if (it == _indexMap.end()){return -1;}return FindRoot(it->second);}// 合并两个元素所在的集合void Union(const T& a, const T& b){int rootA = FindRoot(a);int rootB = FindRoot(b);if (rootA == -1 || rootB == -1 || rootA == rootB)return;// 按秩合并：将小树合并到大树上if (_size[rootA] < _size[rootB]){_parent[rootA] = rootB;_size[rootB] += _size[rootA];}else{_parent[rootB] = rootA;_size[rootA] += _size[rootB];}_setCount--;}// 批量合并void Union(std::initializer_list<std::pair<T, T>> pairs){for (const auto& pair : pairs){Union(pair.first, pair.second);}}// 判断两个元素是否属于同一集合bool IsSameSet(const T& a, const T& b){int rootA = FindRoot(a);int rootB = FindRoot(b);return (rootA != -1 && rootB != -1 && rootA == rootB);}// 获取集合个数size_t GetSetCount() const{return _setCount;}// 根据集合根节点显示集合内所有元素void DisplaySetByRoot(const T& rootElement){int rootIndex = FindRoot(rootElement);if (rootIndex == -1){std::cout << "元素不存在或不是根节点!" << std::endl;return;}std::cout << "集合根节点 '" << _data[rootIndex] << "' 包含的元素:" << std::endl;for (size_t i = 0; i < _data.size(); ++i){if (FindRoot(i) == rootIndex){std::cout << "  编号 " << i << ": " << _data[i] << std::endl;}}}// 显示所有集合void DisplayAllSets(){std::cout << "总共 " << _setCount << " 个集合:" << std::endl;unordered_set<int> displayedRoots;for (size_t i = 0; i < _data.size(); ++i){int root = FindRoot(i);if (displayedRoots.find(root) == displayedRoots.end()){displayedRoots.insert(root);std::cout << "集合 " << root << " (根节点: '" << _data[root] << "'): ";vector<T> elements;for (size_t j = 0; j < _data.size(); ++j){if (FindRoot(j) == root){elements.push_back(_data[j]);}}for (size_t k = 0; k < elements.size(); ++k){std::cout << elements[k];if (k < elements.size() - 1) std::cout << ", ";}std::cout << std::endl;}}}// 根据编号查找元素所在集合的根节点内容T GetSetRootByIndex(int index){if (index < 0 || index >= _data.size()){return T();}int rootIndex = FindRoot(index);return _data[rootIndex];}// 根据元素值查找所在集合的根节点内容T GetSetRootByElement(const T& element){int rootIndex = FindRoot(element);if (rootIndex == -1) return T();return _data[rootIndex];}// 获取集合大小size_t GetSetSize(const T& element){int rootIndex = FindRoot(element);if (rootIndex == -1) return 0;return _size[rootIndex];}// 获取所有元素const vector<T>& GetElements() const{return _data;}// 检查元素是否存在bool Contains(const T& element) const{return _indexMap.find(element) != _indexMap.end();}private:vector<T> _data;map<T, int> _indexMap;vector<int> _parent;vector<int> _size;size_t _setCount = 0;};
}

        测试代码：

//test2.cpp
#include"UnionFindSet.h"
//并查集的数据结构实现
// 测试示例
int main()
{// 测试1: 使用列表初始化DSU::UnionFindSet<string> ufs1 = { "Alice", "Bob", "Charlie", "David", "Eve" };std::cout << "测试1 - 列表初始化:" << std::endl;ufs1.DisplayAllSets();std::cout << "集合个数: " << ufs1.GetSetCount() << std::endl;std::cout << std::endl;// 测试2: 使用列表初始化 + 批量合并DSU::UnionFindSet<string> ufs2 = { "Alice", "Bob", "Charlie", "David", "Eve" };// 使用initializer_list进行批量合并ufs2.Union({ {"Alice", "Bob"}, {"Charlie", "David"}, {"Bob", "Charlie"} });std::cout << "测试2 - 批量合并后:" << std::endl;ufs2.DisplayAllSets();std::cout << "集合个数: " << ufs2.GetSetCount() << std::endl;std::cout << std::endl;// 测试3: 默认构造 + 批量添加DSU::UnionFindSet<string> ufs3;ufs3.AddElements({ "Apple", "Banana", "Cherry", "Date", "Elderberry" });std::cout << "测试3 - 批量添加元素:" << std::endl;ufs3.DisplayAllSets();std::cout << "集合个数: " << ufs3.GetSetCount() << std::endl;std::cout << std::endl;// 合并操作ufs3.Union("Apple", "Banana");ufs3.Union("Cherry", "Date");std::cout << "测试3 - 合并后:" << std::endl;ufs3.DisplayAllSets();std::cout << "集合个数: " << ufs3.GetSetCount() << std::endl;return 0;
}

并查集的应用

        省份数量

        题目链接：https://leetcode.cn/problems/bLyHh0/

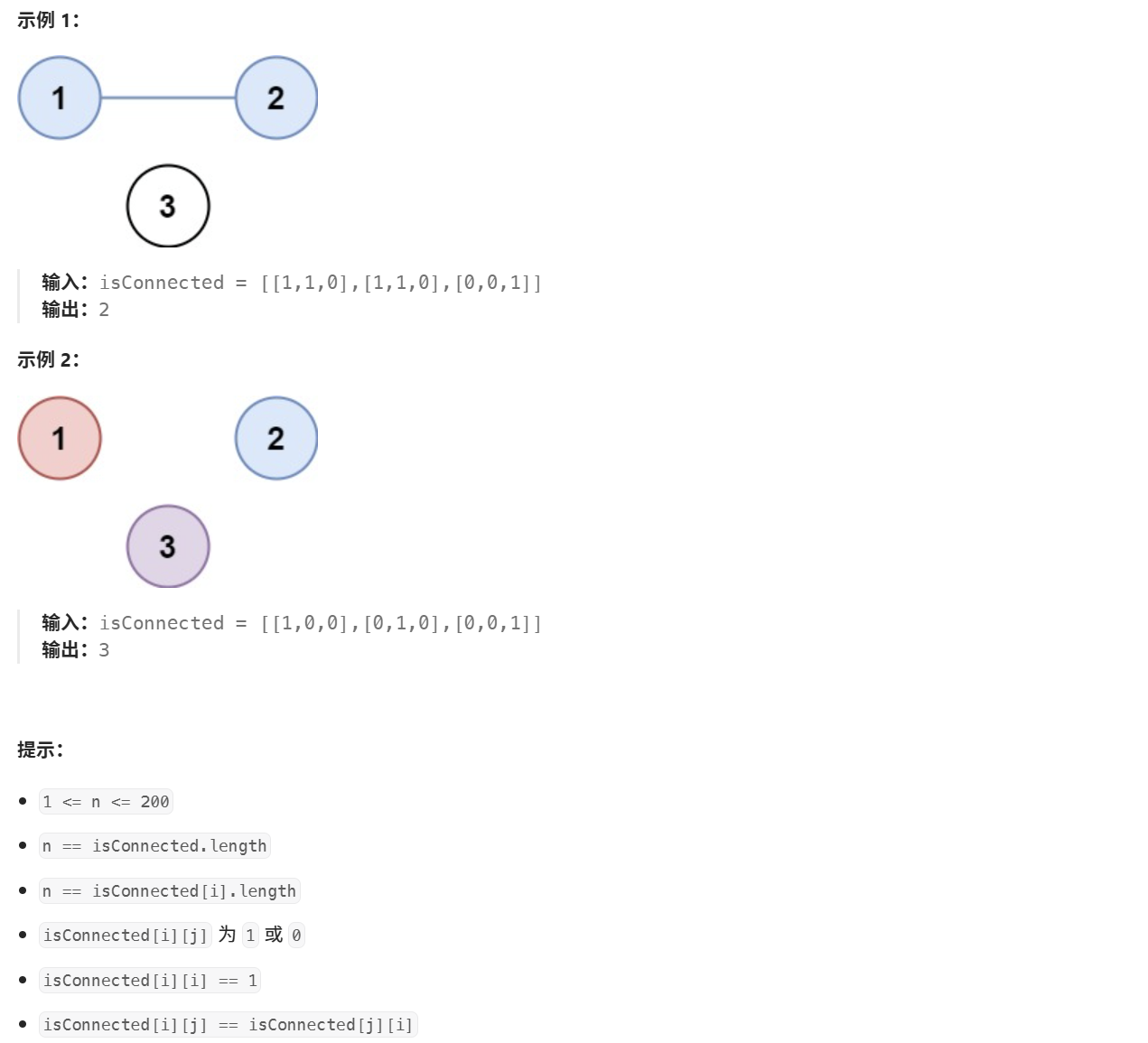
        算法思路：

        使用并查集(Union-Find)数据结构来解决：

  1. 初始化：每个城市自成一个集合

  2. 合并操作：遍历所有连接关系，将相连的城市合并到同一集合

  3. 统计结果：最后统计有多少个独立的集合

        答案：

class Solution
{
public:int findCircleNum(vector<vector<int>>& isConnected){// 手动控制并查集// ufs数组表示并查集，初始时每个元素都是根节点，值为负数表示集合大小// 例如：ufs[i] = -1 表示城市i是根节点，所在集合大小为1vector<int> ufs(isConnected.size(), -1);// 查找根节点的lambda函数// 通过不断向上查找父节点，直到找到根节点（值为负数的节点）auto findRoot = [&ufs](int x){// 一直向上查找，直到找到根节点（ufs[x] < 0）while (ufs[x] >= 0)x = ufs[x];  // 移动到父节点return x;  // 返回根节点的索引};// 遍历所有城市连接关系for (size_t i = 0; i < isConnected.size(); ++i){for (size_t j = 0; j < isConnected[i].size(); ++j){// 如果城市i和城市j相连if (isConnected[i][j] == 1){// 查找两个城市所在的根节点int root1 = findRoot(i);int root2 = findRoot(j);// 如果根节点不同，说明属于不同集合，需要合并if (root1 != root2){// 合并策略：将小集合合并到大集合中// 更新大集合的大小（两个集合大小相加）ufs[root1] += ufs[root2];// 将小集合的根节点指向大集合的根节点ufs[root2] = root1;}}}}// 统计省份数量：即统计有多少个根节点（值为负数的元素）int n = 0;for (auto e : ufs){if (e < 0)  // 负值表示这是一个根节点++n;    // 每个根节点代表一个省份}return n;}
};

        等式方程的可满足性

        题目链接：990. 等式方程的可满足性 - 力扣（LeetCode）

        算法思路

        使用并查集(Union-Find)数据结构来解决：

  1. 处理等式：将所有等式连接的变量合并到同一集合

  2. 验证不等式：检查所有不等式连接的变量是否在不同集合中

        关键洞察

  • 等式具有传递性：如果a == b且b == c，那么a == c

  • 不等式必须与所有等式链保持一致

        冲突检测逻辑：

if (root1 == root2) return false;

        答案：

class Solution {
public:bool equationsPossible(vector<string>& equations){// 初始化并查集，26个小写字母对应0-25的索引// 初始时每个字母自成一个集合，用-1表示（根节点，集合大小为1）vector<int> ufs(26, -1);// 查找根节点的lambda函数auto findRoot = [&ufs](int x){// 不断向上查找，直到找到根节点（值为负数的节点）while (ufs[x] >= 0)x = ufs[x];  // 移动到父节点return x;        // 返回根节点索引};// 第一遍遍历：处理所有等式，构建等价关系for (auto& str : equations){// 只处理等号方程if (str[1] == '='){// 获取两个字母对应的索引（'a'->0, 'b'->1, ..., 'z'->25）int root1 = findRoot(str[0] - 'a');int root2 = findRoot(str[3] - 'a');// 如果两个字母不在同一集合，需要合并if (root1 != root2){// 合并策略：按大小合并，将小集合合并到大集合// 更新大集合的大小（两个集合大小相加）ufs[root1] += ufs[root2];// 将小集合的根节点指向大集合的根节点ufs[root2] = root1;}}}// 第二遍遍历：检查所有不等式是否与已建立的等价关系冲突for (auto& str : equations){// 只处理不等号方程if (str[1] == '!'){// 查找两个字母的根节点int root1 = findRoot(str[0] - 'a');int root2 = findRoot(str[3] - 'a');// 如果两个字母在同一个集合中，说明它们应该相等// 但这与不等式矛盾，返回falseif (root1 == root2){return false;}}}// 所有不等式都通过了检查，没有冲突return true;}
};

        本期关于并查集的内容到这里就结束了，喜欢请点个赞支持一下谢谢

封面图自取：

http://www.dtcms.com/a/578506.html

相关文章：

  • 牛牛网站开发如何弄一个自己的网站
  • 云计算产品-介绍--计算篇
  • 岳池网站建设珠海seo海网站建设
  • 技术解析：鸿蒙 PC 为什么采用 aarch64 架构？
  • B样条曲线降阶方法介绍
  • SciPy 图结构
  • 深圳本地网站建设做酒业网站的要求
  • Linux下查看指定内容的完整日志
  • 做网站 用什么兼容学院网站设计模板
  • 财务分析怎么做？4大关键模块手把手教你做！
  • 【计算机软件资格考试】软考综合知识题高频考题及答案解析6
  • 电商商城网站建设方案wordpress博客xiu
  • wangEditor在弹窗中的销毁注意事项，报错Error: Cannot resolve a Slate range from DOM rang
  • 防滑齿分布与牙钳防滑效能的关系
  • 商城网站网络公司wordpress主题 报纸
  • 站长工具seo诊断潍坊专业网站建设哪家便宜
  • 嵌入式Linux系统性能优化：深入剖析I/O性能瓶颈
  • 计算机操作系统：外存的组织方式
  • 【MCU控制 初级手札】1.7 离子、离子反应 【化学基础】
  • QML学习笔记（五十二）QML与C++交互：数据转换——时间和日期
  • 大模型agent技术
  • 松原市网站建设网站导航栏设计要求
  • 北京专业网站制作介绍大学生二手书网站开发需求
  • spark df 写入lanceDB
  • WebSocket 前端node启用ws调试
  • ArcGIS与ENVI在生态影响评价中的融合应用：八大专题图制作全解析
  • AI赋能企业办公：文多多AiPPT以技术创新破解行业痛点
  • 网站建设用哪的图片不侵权语言 网站开发
  • 网站建设公司的前景字体设计素材网
  • 嵌入式单片机各种通信（UART/RS232/RS485/I2C/CAN/ SPI）