C++ 链表 模拟 递归 迭代 力扣 24. 两两交换链表中的节点 题解 每日一题

题目描述

题目链接：力扣 24. 两两交换链表中的节点

题目描述：

示例 1：

输入：head = [1,2,3,4]
输出：[2,1,4,3]

示例 2：
输入：head = []
输出：[]

示例 3：
输入：head = [1]
输出：[1]

提示：
链表中节点的数目在范围 [0, 100] 内
0 <= Node.val <= 100

为什么这道题值得我们花几分钟看懂？

这道题是链表操作的“进阶训练场”，更是面试高频必刷题并且它多次以基础题或衍生题形式出现。看似简单的节点交换，背后藏着面试中尤为看重的3项核心能力，掌握它能让我们在面试中快速脱颖而出：

1. 深化多指针协同的理解：链表交换是“多指针操作”的经典场景，面试官通过这道题考察我们是否能精准控制指针移动与指向变更。这种能力是解决k个一组翻转、链表重排等复杂链表题的核心基础，而这类题正是大厂区分候选人水平的关键。

2. 掌握递归与迭代的转换思维：同一问题的两种解法，恰好对应面试中“思路灵活性”的考察点。面试官常追问“能否用另一种方法实现”，递归的子问题分解思想、迭代的过程模拟逻辑，能体现我们对算法设计的深度理解，而非只会死记硬背代码。

3. 强化边界条件处理能力：空链表、单节点、奇数长度链表等边界情况，是面试中“代码鲁棒性”的高频扣分点。这道题能帮我们养成“先考虑异常情况”的编程习惯，避免实际开发和面试中的空指针异常——要知道，面试官对“没处理边界条件”的容忍度极低，而严谨的边界处理往往是拿到offer的加分项。

这道题看似是中等难度的基础题，实则是面试官“以小见大”的考察工具：不仅检验我们对链表的理解，更看重代码实现的熟练度、逻辑严谨性和问题拆解能力。花时间吃透它，既能应对直接考察，又能为解决更复杂的链表问题打下基础，性价比极高，值得深入钻研。

算法原理

递归思路

递归的核心在于将复杂问题拆解为规模更小的子问题，通过解决子问题并整合结果得到原问题的解。在实现时，我们只需聚焦于单个子问题，同时坚信递归调用能返回预期结果（即“递归信仰”），这种思路在链表两两交换问题中体现得尤为透彻。

递归函数的定位
递归函数的任务是传入一个链表的头节点，函数会将该节点后续的链表进行两两交换，并返回交换后的新头节点。这与题中所给的函数体完全吻合，为递归实现奠定了基础。

ListNode* swapPairs(ListNode* head) { ... }

递归过程解析

1. 先递归处理当前节点之后的链表，确保后续部分已完成两两交换。
2. 再处理当前的两个节点，完成交换后与已处理的后续链表连接。
3. 最终返回交换后的新头节点，供上层递归使用。

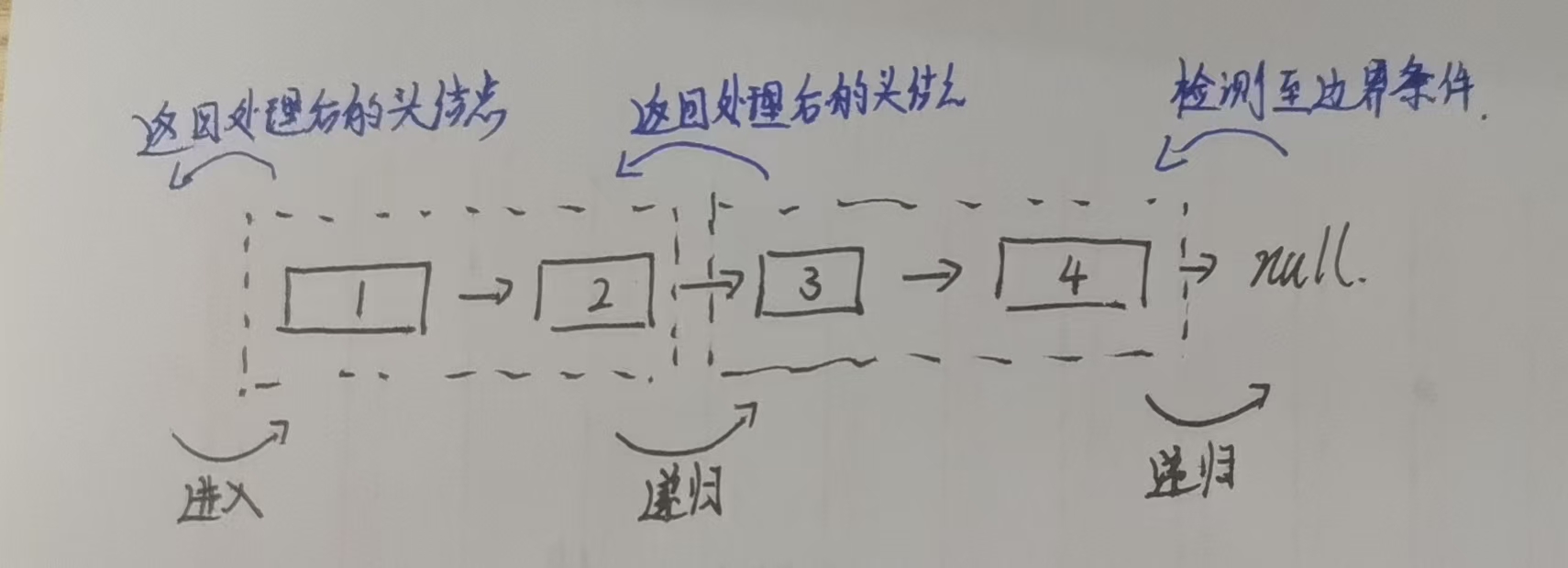
形象来说，就像从链表末尾开始，先完成最末端的两两交换，再逐步向前处理，每一步都只需关注眼前的两个节点和已处理好的后续部分。

关键细节处理

1. 递归终止条件
   当传入的节点为空（head == nullptr）或只剩一个节点（head->next == nullptr）时，无需交换，直接返回当前节点，避免无效递归。

2. 连接子问题结果
   递归处理完后续链表后，会得到一个已交换完成的子链表头节点。需将当前交换后的第二个节点与该子链表头节点连接，确保链表的连续性。

3. 返回新头节点
   两两交换后，原第二个节点会成为新的头节点，因此需将其返回给上层递归，作为当前子问题处理结果的起点。

通过这种递归思路，我们无需手动维护复杂的指针关系，只需聚焦于单步交换逻辑，借助递归的“自底向上”特性，就能高效、清晰地完成链表的两两交换，在实现代码的时候我们思路只需要聚焦处理当前节点的交换即可，坚信在当前调用的递归函数返回给我的是预期结果即可，这样我们在实现递归代码时候思路就会非常清晰，不会被递归层数弄乱。

迭代思路

我发现当定义多个指针的时候讲解与理解起来会非常轻松，所以迭代思路我们结合图片直接将迭代的思路秒了，如下图👇：

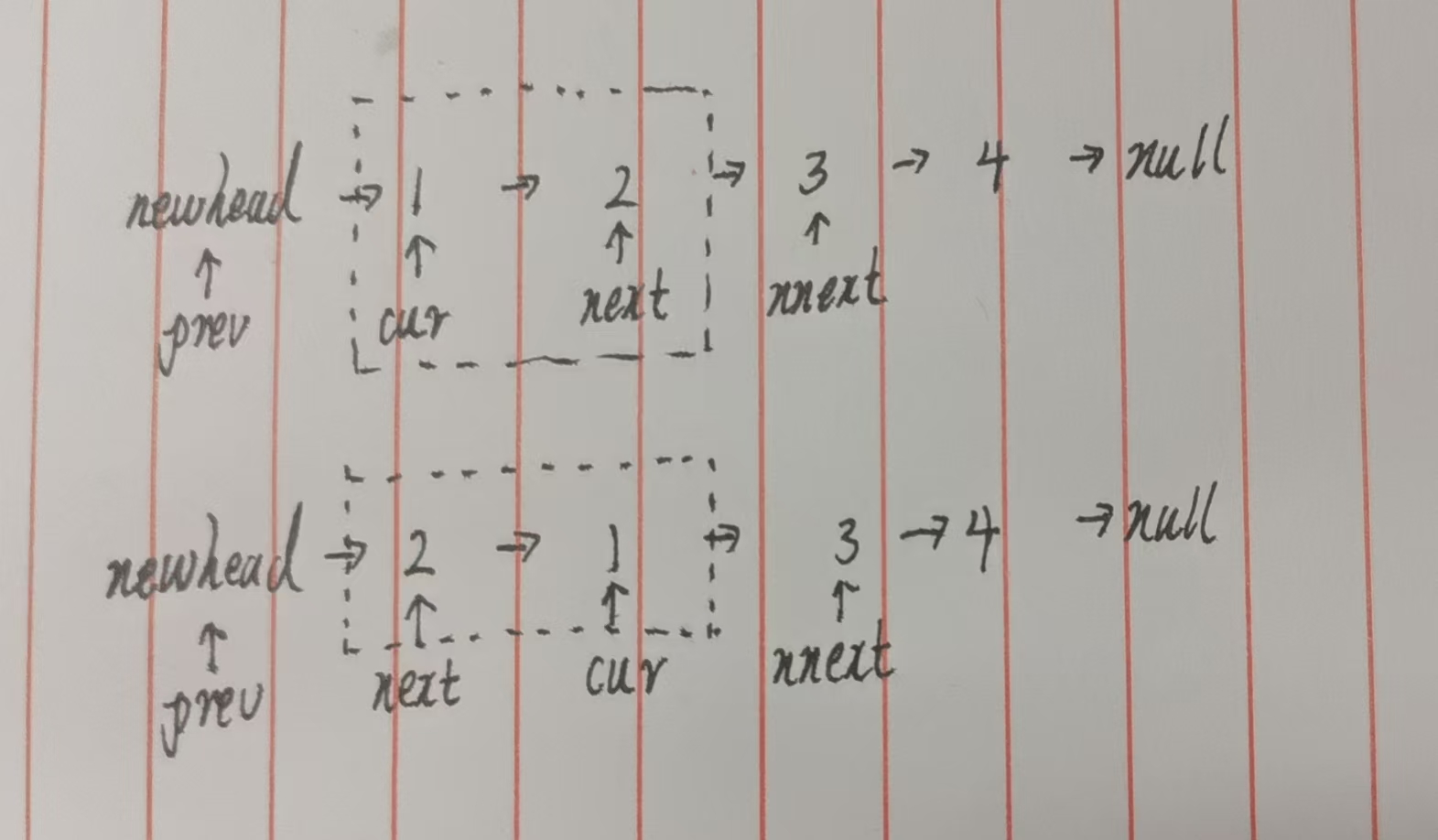
当我们定义四个指针之后我们会发现在交换逻辑就是看图说话，因为我们指针足够多根本不用考虑节点丢失的情况。

向后移动同样，对照下面的图片看图说话即可（蓝框部分）👇：

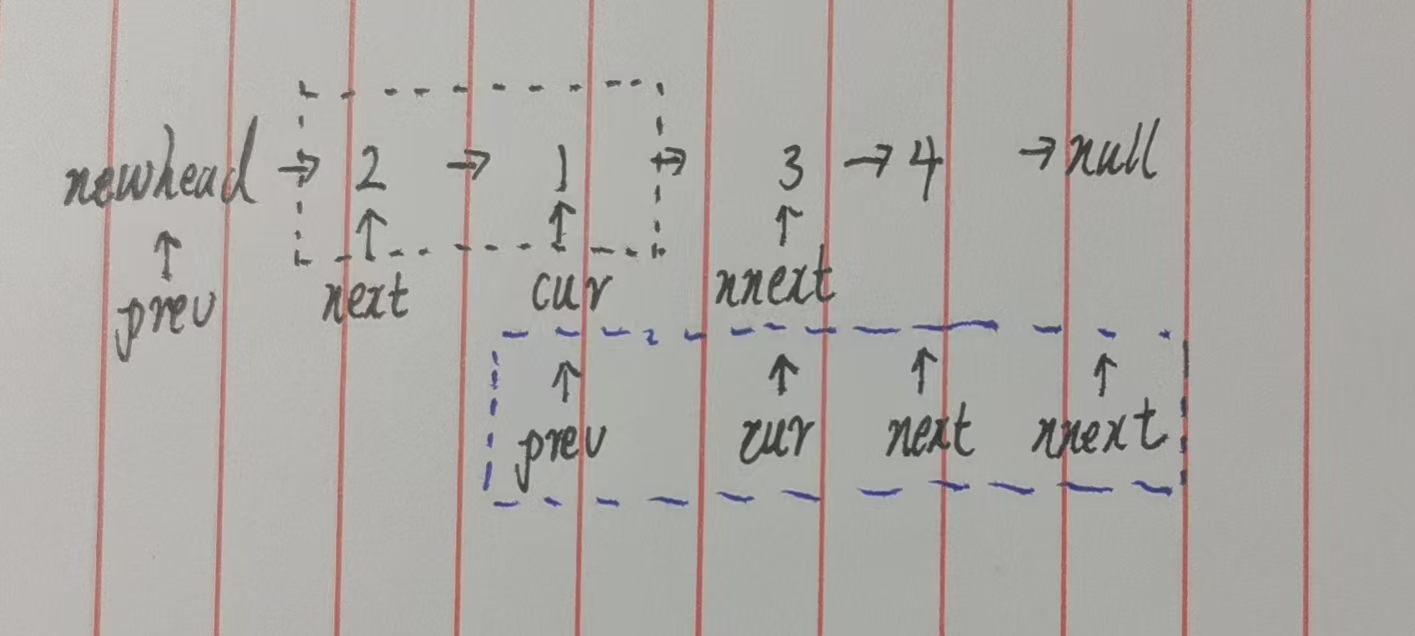
关键细节处理

1.节点定义的重要性：
对链表操作不熟悉时，不要吝啬定义临时节点（如 cur、next、nnext），清晰的节点命名能降低逻辑复杂度，临时节点可直观记录各位置的节点，避免因连续使用 next->next 导致的指针关系混乱（当然大佬这里就可以跳过了）

2.空指针解引用问题：
我们这样定义要注意的就是空指针解引用问题，这个是尤为致命的。

3.边界情况分析：
通过 while(cur && next) 循环条件，自动跳过长度不足的组（如奇数长度链表的最后一个节点）

希望到了这里大家可以尝试自己写下代码感受一下，因为这种题目思路并不是很难，难点在锻炼我们的代码实现的能力，上面的思路中我也尽可能的少出现了关于变量命名或者是有关代码实现的部分，尤其迭代思路中的空指针解引用问题，出现空指针解引用问题不要慌自己仔细画图分析下没问题的！（当然细节处理上我会在实现代码之后结合代码详细解释）

---

代码实现

递归版本代码

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {// 递归终止条件：空链表或只有一个节点，无需交换if(head == nullptr || head->next == nullptr)return head;// 递归处理剩余子链表，得到交换后的子链表头节点ListNode* finish = swapPairs(head->next->next);// 定义当前组的两个节点ListNode* cur1 = head;ListNode* cur2 = head->next;// 交换当前组节点，并连接子链表结果cur1->next = finish;cur2->next = cur1;// 返回交换后当前组的头节点（即原cur2）return cur2;}
};

迭代版本代码

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {// 边界条件：空链表或单节点链表直接返回if(head == nullptr || head->next == nullptr)return head;// 创建虚拟头节点，简化头节点交换逻辑ListNode* newhead = new ListNode();newhead->next = head;// 初始化指针：前驱节点、当前组节点及下一组节点ListNode* prev = newhead;ListNode* cur = prev->next;ListNode* next = cur->next;ListNode* nnext = next->next;// 循环处理每一组节点（需存在两个节点）while(cur && next){// 交换当前组节点prev->next = next;next->next = cur;cur->next = nnext;// 更新指针，准备处理下一组prev = cur;cur = nnext;if(cur != nullptr)     next = cur->next;  // 避免空指针访问if(next != nullptr)    nnext = next->next; // 避免空指针访问}// 释放虚拟头节点内存，更新结果头节点head = newhead->next;delete newhead;return head;}
};

关键细节分析

1.空指针解引用问题
最开始的指针定义空指针问题：

所以我们在代码中要进行判断验证，这两种情况都可以直接返回链表即代码中

if(head == nullptr || head->next == nullptr)return head;

循环中的空指针引用问题：


所以在循环中我们也要加验证判断：

if(cur != nullptr)     next = cur->next;  // 避免空指针访问
if(next != nullptr)    nnext = next->next; // 避免空指针访问

2.指针向后移动问题

prev = cur;
cur = nnext;

这里的顺序很重要不能反过来，prev 指向的位置本来是原来的 cur 指向的位置，当先执行 cur = nnext 之后 prev 就会指向 nnext 很明显不是我们预期的位置

时间复杂度与空间复杂度分析

• 递归版本：

  • 时间复杂度：O(n)，其中 n 是链表节点数，每个节点仅被访问一次
  • 空间复杂度：O(n)，递归调用栈的深度为 n/2（每处理两个节点递归一次）

• 迭代版本：

  • 时间复杂度：O(n)，每个节点仅被访问一次
  • 空间复杂度：O(1)，仅使用常数个额外指针变量

总结

1. 核心思路：

   • 递归：通过分解子问题，先解决剩余链表的交换，再处理当前组节点的交换与连接
   • 迭代：利用虚拟头节点统一逻辑，通过多指针循环处理每组节点的交换，确保链表连续性

2. 关键技巧：

   • 递归中明确终止条件和子问题边界，避免无限递归
   • 迭代中通过虚拟头节点简化头节点处理，多指针记录节点位置防止链表断裂
   • 重视空指针判断，避免解引用错误

3. 面试注意：

   • 能清晰讲解递归与迭代两种思路的区别及适用场景
   • 手动模拟指针移动过程，展示对链表操作的熟练度
   • 关注内存管理（如释放虚拟头节点），体现编程规范性

下题预告

接下来，我们将聚焦链表操作中另一道经典题目——力扣 143. 重排链表。这道题堪称链表操作的“综合训练场”，需要我们灵活运用链表的反转、中点查找、合并等多种核心技巧：既要精准找到链表中点分割链表，又要熟练反转后半段，最终将两个子链表按特定规则交织合并。我们会拆解每一步的实现逻辑，分析时间与空间的优化思路，带你掌握“分而治之”在链表问题中的实战应用。

坚持跟着梳理的朋友，相信对链表的操控能力会再上一个台阶！如果这篇两两交换的解析对你有帮助，欢迎点赞收藏，方便随时回顾～ 关注博主，下一篇我们一起攻克重排链表的难点，让每一步学习都扎实落地！

Doro 带着小花🌸来啦！🌸奖励🌸看到这里的你！如果这篇内容帮你理清了两种不同的的解题逻辑，或是让你对反转链表操作的代码有了更清晰的认识，别忘了点赞支持呀！把它收藏起来，以后复习这类问题时翻出来，就能快速回忆起关键细节～关注这个博主，他会持续更新算法系列内容，有什么疑问或者好的建议发到评论区他看到会及时认真回复哒！