汽车信息安全--关于安全强度的误区

估摸着是《汽车整车信息安全技术要求》执行时间的临近，很多Tier1都开始着手给自己的件加上信息安全，首先就是安全启动功能。

最近接触了很多客户，关于安全启动校验算法是选非对称还是对称算法，我发现普遍存在一个误区：认为安全强度只和密钥长度有关，例如RSA2048的安全强度远高于AES128，因为2048远远大于128。

事实上，根据NIST SP 800-57 5.6.1 Comparable Algorithm Strengths章节描述，安全强度首先是依赖密码算法，其次才是密钥长度。

这里给出“安全强度”的定义：

A security strength is a number associated with the amount of work (i.e., the number of operations) that is required to  break a cryptographic algorithm or system.

从定义我们不能难看出，密码算法底层原理的复杂性才是决定安全强度的前提。

我们来看看这其中区别。

AES是一种对称分组密码，加密和解密使用相同密钥，对数据进行固定长度分组进行处理，它的处理过程围绕着轮函数进行。

我们以一个魔方的打乱和还原来描述，整齐的魔方作为明文，密钥是打乱的具体顺序，密码算法则是固定转动规则（例如魔方只能横竖90度、一排、两排等等转动，这是公开且每个人都明白的），按照密钥将魔方打乱得到密文，也可以很容易按照密钥将魔方还原得到明文，但是没有密钥的人不知道具体顺序，很难去进行破解。

很明显，密钥越长，顺序越多，破解难度就越大，例如128位密钥，意味着密钥空间为2^128，具体=​340,282,366,920,938,463,463,374,607,431,768,211,456​。用暴力破解的手段，这对于目前计算能显然是不可行的。

RSA的安全性则来源于大整数分解的数学难题，例如RSA2048使用的是2048位模数，破解它完全不需要尝试2^2048次，而只是需要去把这个数进行分解，而据NIST标准上的介绍，RSA-2048的安全强度等同于对称算法的112位。

那么为什么椭圆曲线算法的密钥长度也不算很长，安全强度也不错呢？

这仍旧是底层原理所致，椭圆曲线算法是基于离散对数的数学难题，具体原理我们之前讲过，实在不想了解，你只需要想象：在一个台球桌上，你仅仅知道白球的起点和终点，让你说出白球经历了多少次的碰撞才到达终点。这个难度，还是非常具体。

因此，NIST给出了不同算法的安全强度对比地图：

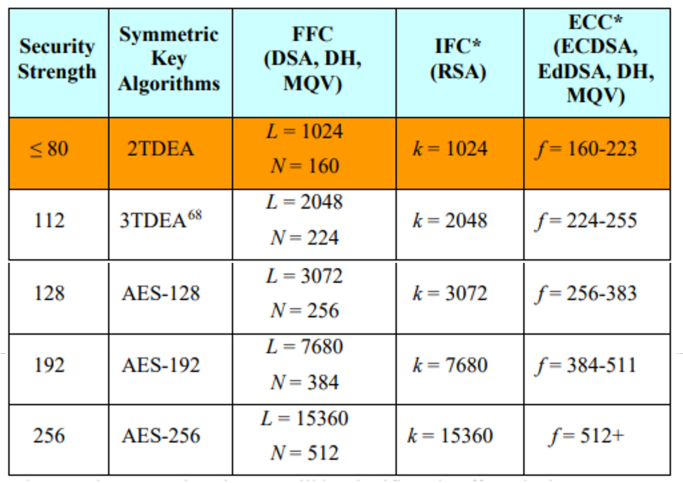
这样大家就不会感到困惑了。

此外，从各算法的底层原理上我们也能明白，采用AES-CMAC的校验速度会比RSA\ECC等验签的速度快很多的原因，具体不多讲了。

就酱，拜拜