力扣1539. 第 k 个缺失的正整数

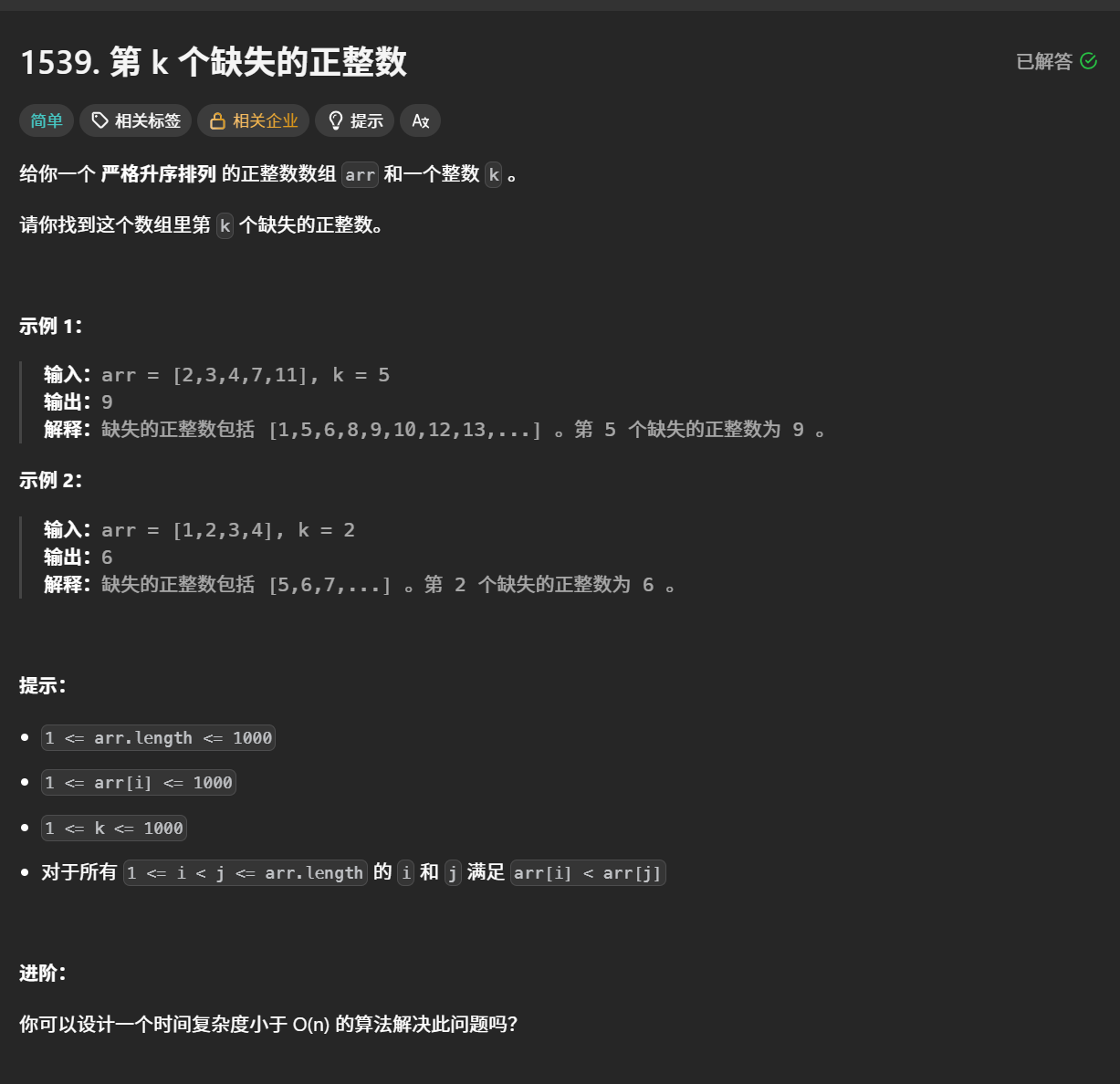
这一题的大意是说给出一个数组，和一个整数k，这个数组是严格升序排列的，现在让我们找第k个缺失的正整数。
什么叫做第k个缺失的正整数呢？意思是数组应该是从自然数1开始1…2…3正常排列的，但现在有缺失的，让我们找第k个缺失的数是多少？
那么我们如何可以判断呢，题目上让用一个小于logn的算法，又因为是让求第K个缺失的数，很明显是用二分。
那么该怎么二分呢？
我们很容易发现要想判断某一数组中缺失多少个数，只需要用 arr[i]-(i+1) (i从0开始）即可求得。
那么我们只需要找第一个大于等于k的数，那么在它的上一个数就是最后一个小于等于k的数，我们只需要用arr[l-1]+k-arr[l-1]-l即算出第k个缺失的数是多少。这里的l表示的是第一个大于等于k的数，而l-1表示的是最后一个小于等于k的数。
这里的第一个arr[l-1]表示从这个往后再加+k-arr[l-1]-l个数就是第k个缺失的数。
而k-arr[l-1]-l表示最后一个小于等于k的数之前已经缺失了这些数，但还没有达到k个，还差k-arr[l-1]-l个数就达到了缺失的第k个数，我们只需要用arr[l-1]+k-arr[l-1]-l即为第k个缺失的数，化简得 k+l
因此代码如下：

class Solution {
public:int findKthPositive(vector<int>& arr, int k) {int l=0;int r=arr.size()-1;while(l<=r){int mid=(l+r)/2;if(arr[mid]-mid-1>=k){r=mid-1;}else{l=mid+1;}}if(l!=0)return (arr[l-1]+(k-(arr[l-1]-l)));else{return k;}}
};

或者

class Solution {
public:int findKthPositive(vector<int>& arr, int k) {int l=0;int r=arr.size()-1;while(l<=r){int mid=(l+r)/2;if(arr[mid]-mid-1>=k){r=mid-1;}else{l=mid+1;}}return l+k;}
};

这一题很容易想到二分，想到找第一个大于等于k的数的位置，但对于第k个数是多少，我觉得很不好想，看题解都是return l+k，但说不清楚l+k的含义。
实际上l+k的含义就是arr[l-1]+k-arr[l-1]-l的数学化简，要理解还是要用arr[l-1]+k-arr[l-1]-l
arr[l-1]+k-arr[l-1]-l即算出第k个缺失的数是多少。
时间复杂度O（logn）
我们也可以直接找最后一个小于k的数的位置，然后直接用arr[r]+k-(arr[r]-(r+1))好理解。

class Solution {
public:int findKthPositive(vector<int>& arr, int k) {int l=0;int r=arr.size()-1;while(l<=r){int mid=(l+r)/2;if(arr[mid]-mid-1<k){l=mid+1;}else{r=mid-1;}}//最后一个小于k的位置if(r==-1){return k;}elsereturn arr[r]+(k-(arr[r]-(r+1)));}
};

这里的r是最终指向的最后一个小于k的位置，这里是跟上面的l的意思是类似的。
我们直接用二分找到最后一个缺失数字小于k的位置用这个位置的值arr[r]+(k-(arr[r]-r-1)(还差多少个数字）从而表示出第k个缺失的数字。
为什么非要找最后一个小于k的位置或者第一个大于等于k的位置，关键就在于我们可以弄清楚 第k个数就在最后一个小于k的位置或者第一个大于等于k的位置之间，只需要在再原有的基础上加上还缺的数字个数即可。