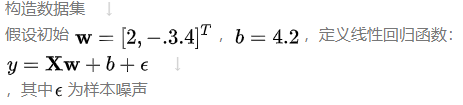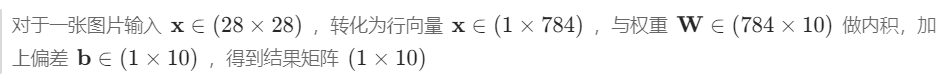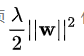李沐动手学深度学习笔记（1）

1. 数据操作与预处理

N 维数组

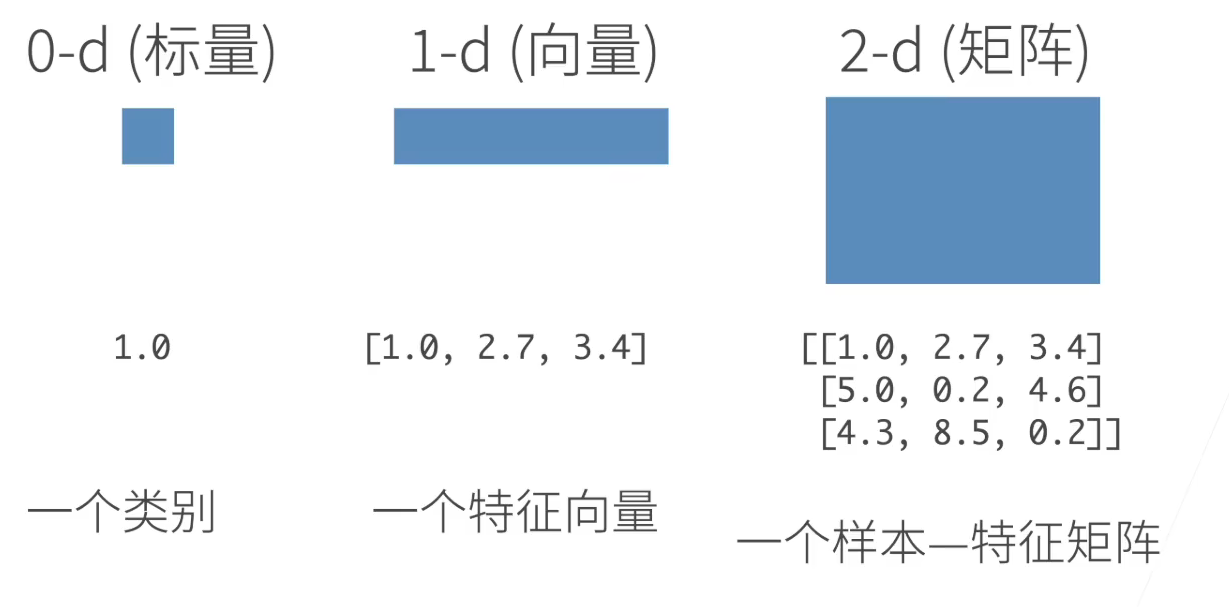
• N=0：标量。一般表示分类问题中指代一个类别
• N=1：向量。一般表示一个样本经过特征化后的特征向量
• N=2：矩阵。一般表示数据集或者其中的 Batch，每一行为一个样本；或一张黑白图片的明暗表示(宽 X 高)
• N=3：一般用于表示一张彩色图像(宽 X 高 X 通道)；或黑白图像数据集(批量大小 X 宽 X 高)
• N=4：一般用于表示彩色图像的数据集或其中的 Batch(批量大小 X 宽 X 高 XRGB 通道)
• N=5：一般用于表示一段视频(批量大小 X 时间 X 宽 X 高 XRGB 通道)

定义矩阵
维度、精度、赋值

数据操作

访问元素

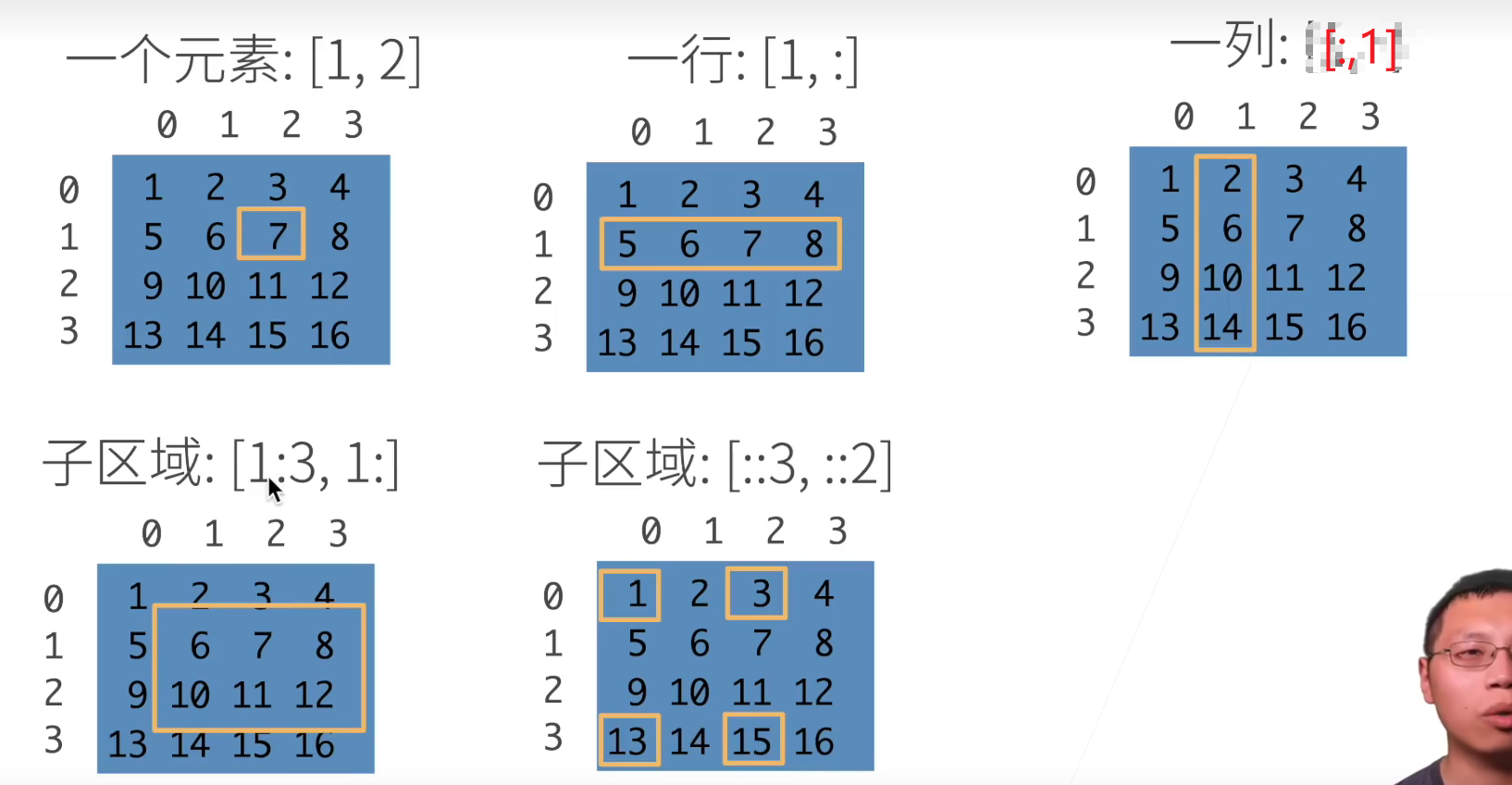
• [1,3]：访问二维数组单一元素
• [2,:]：只有冒号，代表将此维度全部取出
• [1:3,1:]：冒号前后跟数字代表取一个_前闭后开_区间的元素，多在 CNN 中用于在整张图片矩阵中取出一个子区域的数据操作来与卷积核进行运算
• [::3,::2]：两个冒号后代表隔几个元素取，多用于 CNN 中的“空洞卷积”操作

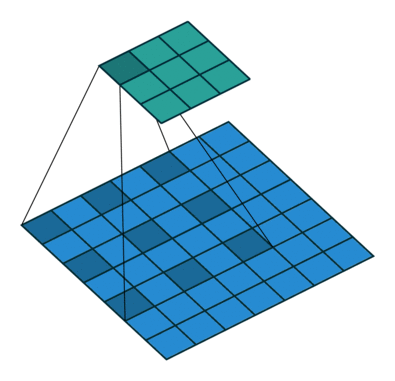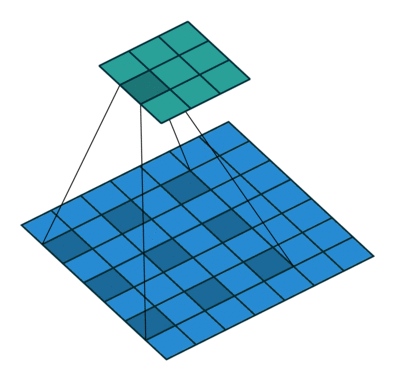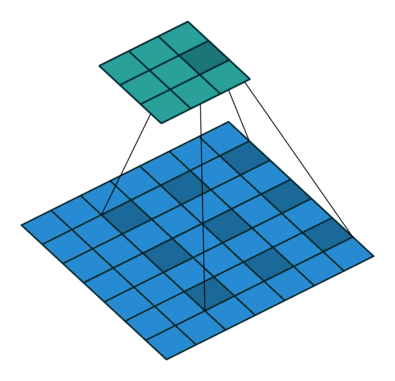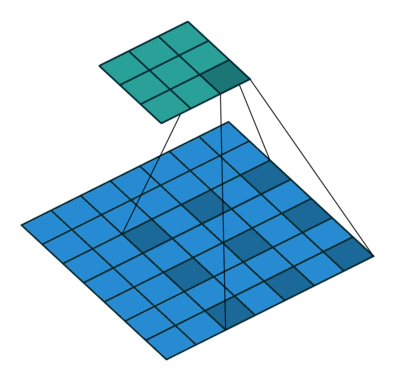
Pytorch 数据基本操作

• torch.arange(N)：生成一个从 0~N-1 的一维 Tensor
• torch.shape：获得张量的形状
• torch.numel()：获得张量中所有元素的个数
• [tensor].reshape(m,n,o...)：将一个 Tensor 重塑为(mno…)形状
• torch.zeros((m,n))：生成一个 m*n的全零张量(一般用于初始化偏置 Bias)
• torch.ones((m,n))：生成一个 m*n 的全 1 张量
• torch.tensor([list])：将 Python 列表转换为张量
• [tensor1]**[tensor2]：按元素求幂运算
• torch.exp([tensor])：按元素求指数
• torch.cat([tensor1],[tensor2],dim=0)：按行(第 0 维)纵向连接两个张量(dim=1 为按列横向连接)，如果维度更高，可以 dim>=2
• torch 继承了 numpy 的广播机制，不同维度的数组可以进行元素运算，但两个数组至少有一个维度相同
• [tensor][X,Y] = m：元素赋值
• [tensor][:]：元素改写，不改变内存地址
• [tensor].sum()：求和所有元素得到标量
• [tensor].numpy()：将张量转换为 Numpy 数组
• torch.tensor([ndarray] | [list] | [Dataframe])：将其他格式数据转换为张量格式
• [tensor].item() | float([tensor]) | int([tensor])：将大小为 1 的张量转换为 Python 标量

import torch
# 初始化一个0~11的张量
x=torch.arange(12)  
x   #tensor([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])x.shape   #torch.Size([12])
# # 张量中元素的总数
x.numel   #12# 改变张量的形状
X=x.reshape(3,4)
X
输出：
tensor([[ 0,  1,  2,  3],[ 4,  5,  6,  7],[ 8,  9, 10, 11]])# 创建全0/全1
torch.zeros((2,3,4))
输出：
tensor([[[0., 0., 0., 0.],[0., 0., 0., 0.],[0., 0., 0., 0.]],[[0., 0., 0., 0.],[0., 0., 0., 0.],[0., 0., 0., 0.]]])torch.ones((2,3,4))
输出：
tensor([[[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.]],[[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.]]])

# 创建特定值的张量
y=pytorch.tensor([[2,1,4,3],[1,2,3,4],[4,3,2,1]]) #二维tesor
输出：
tensor([[2, 1, 4, 3],[1, 2, 3, 4],[4, 3, 2, 1]])z=pytorch.tensor([[[2,1,4,3],[1,2,3,4],[4,3,2,1]]])   # 三维tensor
输出：
tensor([[[2, 1, 4, 3],[1, 2, 3, 4],[4, 3, 2, 1]]])print(y.shape)
print(z.shape)
输出：
torch.Size([3, 4])
torch.Size([1, 3, 4])

# 算数运算
x=torch.tensor([1.0,2,4,8])
y=torch.tensor([2,2,2,2])
x+y,x-y,x*y,x/y,x**y
输出：
tensor([ 3.,  4.,  6., 10.])
tensor([-1.,  0.,  2.,  6.])
tensor([ 2.,  4.,  8., 16.])
tensor([0.5000, 1.0000, 2.0000, 4.0000])
tensor([ 1.,  4., 16., 64.])# 指数运算
torch.exp(x)
print(x)
输出：
tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])

# 把多个张量结合在一起
x=torch.arrange(12,dtype=torch.float32).reshape((3,4))
y=torch.tensor([[2.0,1,4,3],[1,2,3,4],[4,3,2,1]])
torch.cat((x,y),dim=0)  #按行排列
torch.cat((x,y),dim=1)  #按列排列
输出：
tensor([[ 0.,  1.,  2.,  3.],[ 4.,  5.,  6.,  7.],[ 8.,  9., 10., 11.],[ 2.,  1.,  4.,  3.],[ 1.,  2.,  3.,  4.],[ 4.,  3.,  2.,  1.]])
tensor([[ 0.,  1.,  2.,  3.,  2.,  1.,  4.,  3.],[ 4.,  5.,  6.,  7.,  1.,  2.,  3.,  4.],[ 8.,  9., 10., 11.,  4.,  3.,  2.,  1.]])

# 通过逻辑运算符构建二维张量
x==y
输出：
tensor([[False,  True, False,  True],[False, False, False, False],[False, False, False, False]])

# 对张量中所有元素进行求和会产生一个只有一个元素的张量
x.sum()
输出：
tensor(66.)

# 张量广播机制
a=torch.arange(3).reshape((3,1))
b=torch.arange(2),reshape((1,2))
输出：
tensor([[0],[1],[2]])
tensor([[0, 1]])a+b
输出：
tensor([[0, 1],[1, 2],[2, 3]])

# 访问
x = torch.arange(12,dtype=torch.float32).reshape((3,4))
x[-1],x[1:3]
输出：
tensor([ 8.,  9., 10., 11.])
tensor([[ 4.,  5.,  6.,  7.],[ 8.,  9., 10., 11.]])

# 通过指定索引将元素写入矩阵
x[1,2]=9
x
输出：
tensor([[ 0.,  1.,  2.,  3.],[ 4.,  5.,  9.,  7.],[ 8.,  9., 10., 11.]])# 为多个元素赋值
x[0:2,:]=12
x
输出：
tensor([[12., 12., 12., 12.],[12., 12., 12., 12.],[ 8.,  9., 10., 11.]])

# 运行一些操作可能会导致为新结果分配内存
import torch
x = torch.arange(12,dtype=torch.float32).reshape((3,4))
y = torch.tensor([[2.0,1,4,3],[1,2,3,4],[4,3,2,1]])
before = id(y) 
y = x + y
print(id(y) == before) # 运行操作后，赋值后的y的id和原来的id不一样   输出：False

# 张量转numpy
A=x.numpy()
B=torch.tensor(A)
type(A),type(B)输出：
<class 'numpy.ndarray'> <class 'torch.Tensor'># 将大小为1的张量转换为python标量
a=torch.tensor([3.5])
a,a.intem,float(a),int(a)输出：
tensor([3.5000])
3.5
3.5
3

Pandas 数据基本操作

• pd.read_csv(file)：读取 CSV 文件并转换为 Pandas Dataframe 格式
• [Dataframe].iloc[:,0:2]：取出对应索引的数据分片
• [Dataframe].fillna(value)：补充缺失数据
• pd.get_dummies([Dataframe, dummy_na=True])：将离散类别进行 One-hot 编码成数字，同时将缺失值当成一种类别

# 创建一个人工数据集，并存储在csv（逗号分隔符）文件
import pandas as pd
import os
os.makedirs(os.path.join('.','01_Data'),exist_ok=True)
data_file=os.path.join('.','01_Data','01_house_tiny.csv')
with open(data_file,'w') as f:f.write('NumRooms,Alley,Price\n')  #列名f.write('NA,Pave,127500\n')  # 每行表示一个数据样本f.write('2,NA,106000\n')f.write('4,NA,178100\n')f.write('NA,NA,140000\n')

# 加载数据集
data=pd.read_csv(data_file)
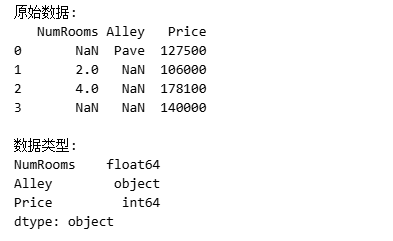
print("原始数据:")
print(data)
print("\n数据类型:")
print(data.dtypes)

# 预处理数据集
# 为了处理缺失的数据，典型的方法包括插值和删除
# inputs：取前两列（0到1列），即特征（输入数据）
# outputs：取第3列（索引2列），即标签（输出数据）
inputs,outputs=data.iloc[:,0:2],data.iloc[:,2]# 只对数值列NumRooms进行均值填充
inputs['NumRooms']=inputs['NumRooms'].fillna(inputs['NumRooms'].mean())
print("处理后的inputs：")
print(inputs)输出：
处理后的inputs:NumRooms Alley
0       3.0  Pave
1       2.0   NaN
2       4.0   NaN
3       3.0   NaN

# 对于inputs中的类别值或离散值，将NaN视为一个类别 
# 使用get_dummies进行独热编码
# dummy_na=True 会为NaN值创建单独的列
inputs_encoded=pd.get_dummies(input,dummy_na=True)
print("独热编码后的inputs:")
print(inputs_encoded)输出：
独热编码后的inputs:NumRooms  Alley_Pave  Alley_nan
0       3.0        True      False
1       2.0       False       True
2       4.0       False       True
3       3.0       False       True

# 数据集转张量
# 直接转成float32
x=torch.tensor(inputs.values.astype(np.float32))
y=torch.tensor(outputs.values.astype(np.float32))
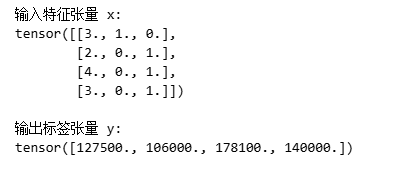
print("输入特征张量 x:")
print(x)
print("输出标签张量 y:")
print(y)

2.线性代数

关于线性代数相关知识，强烈推荐3Blue1Brown的超棒教程 👇

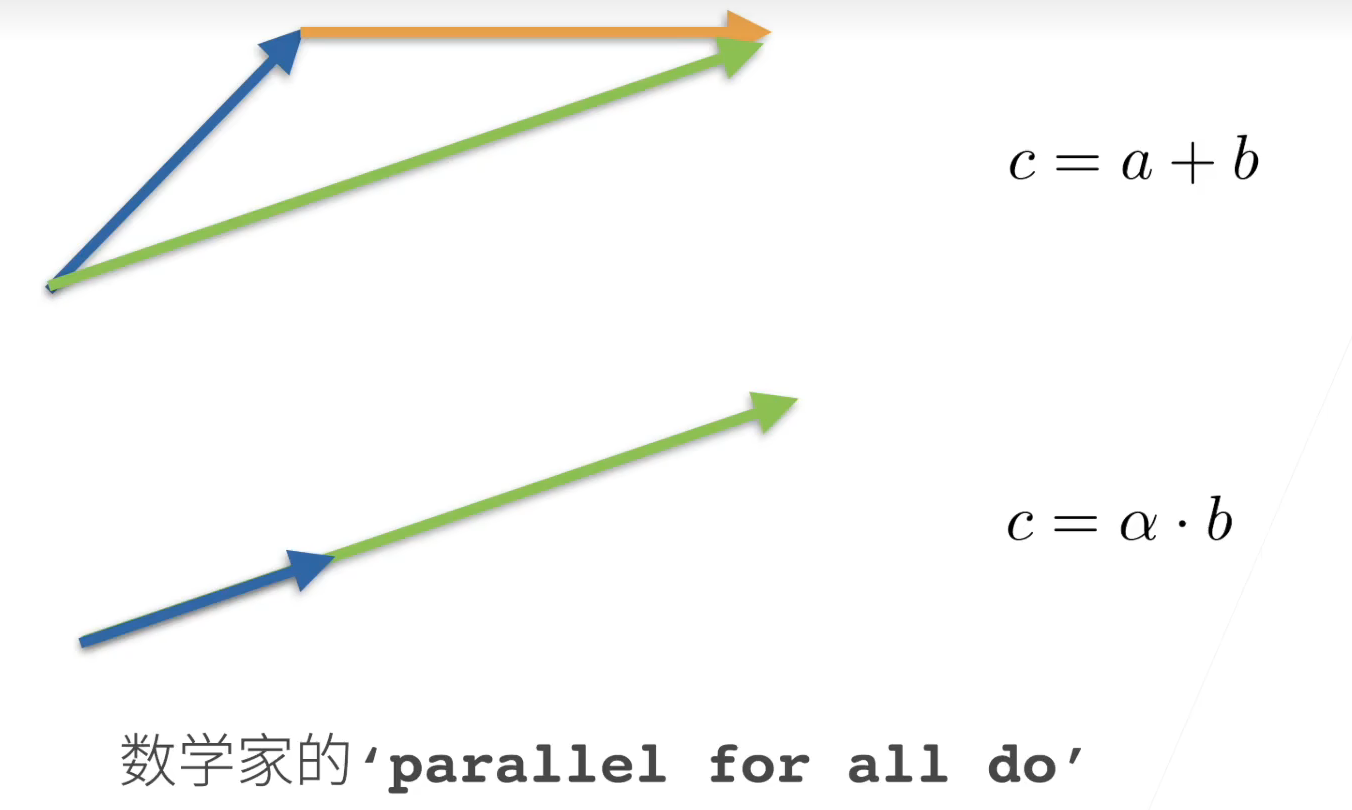
基本概念

1. 标量

2. 向量

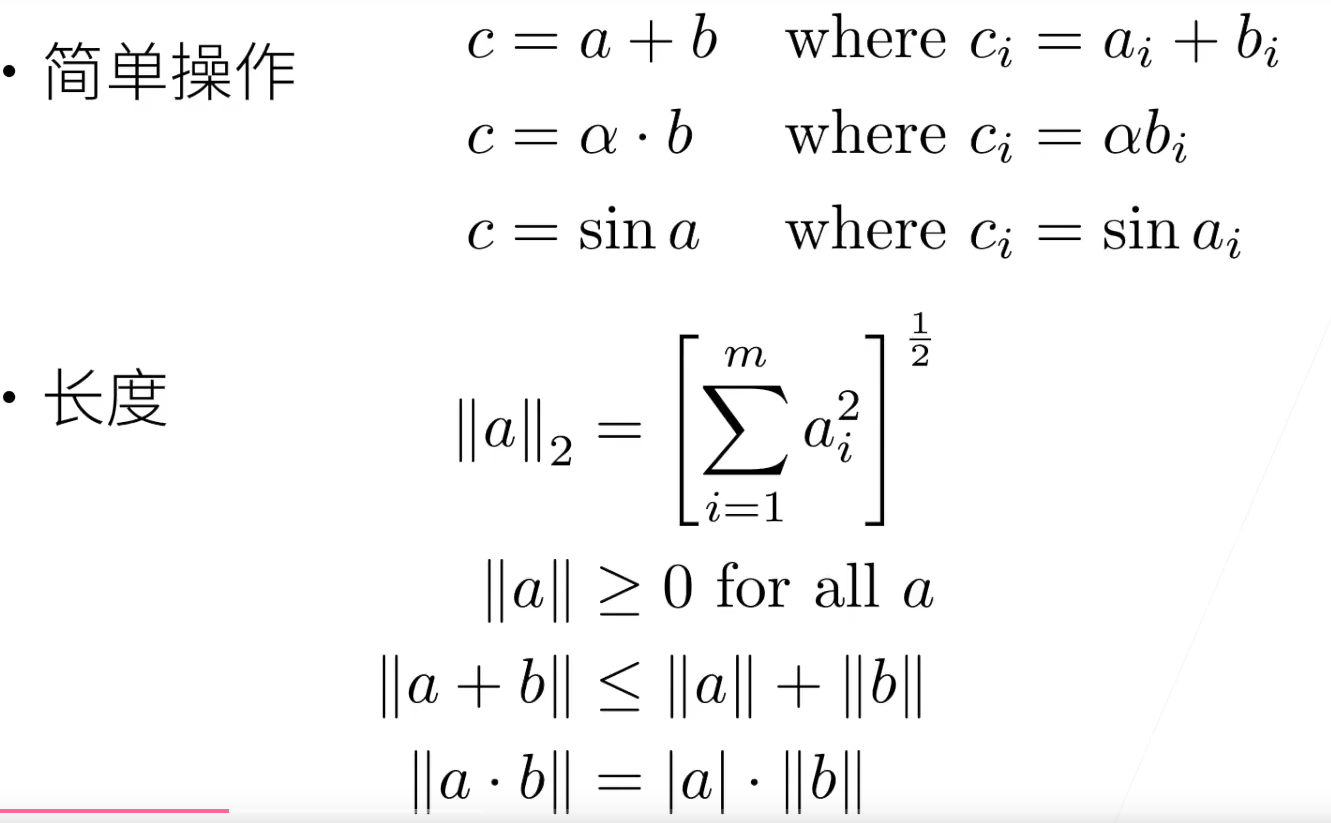
3. 矩阵

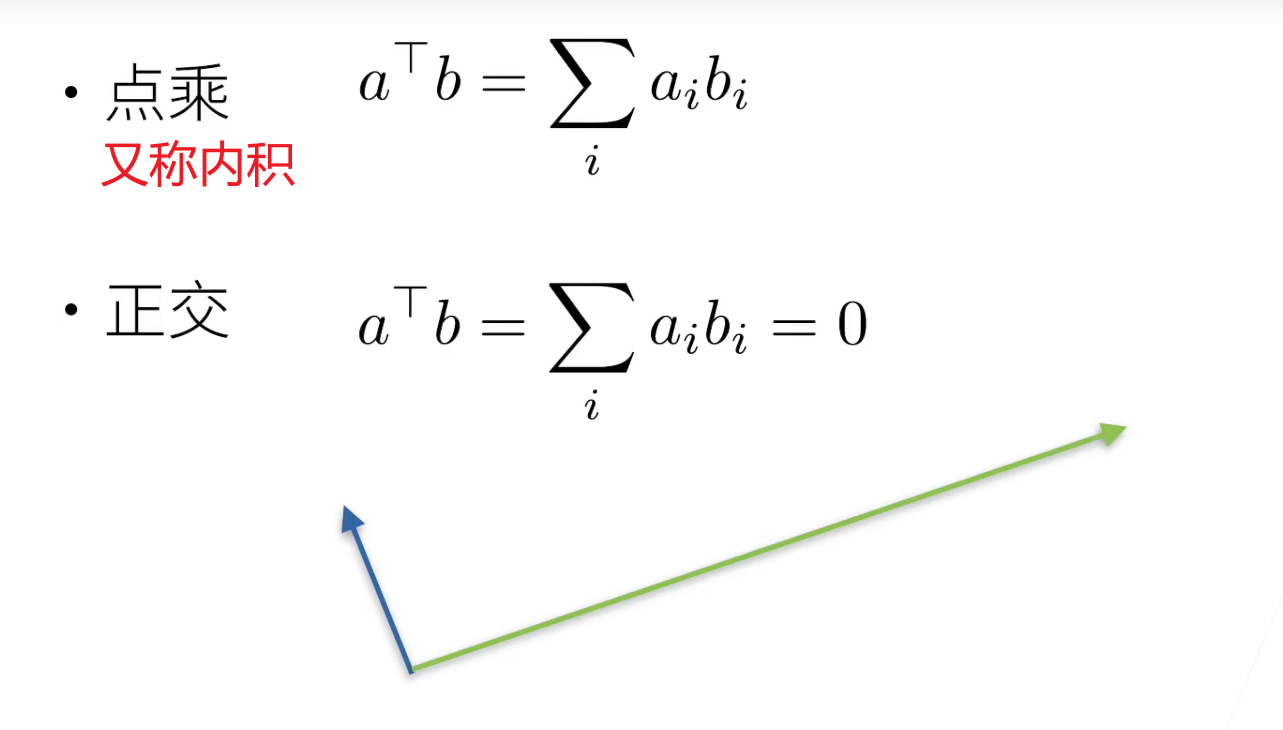
范数（Norm） 就是用来度量一个向量的“长度”或“大小” 的数学工具。

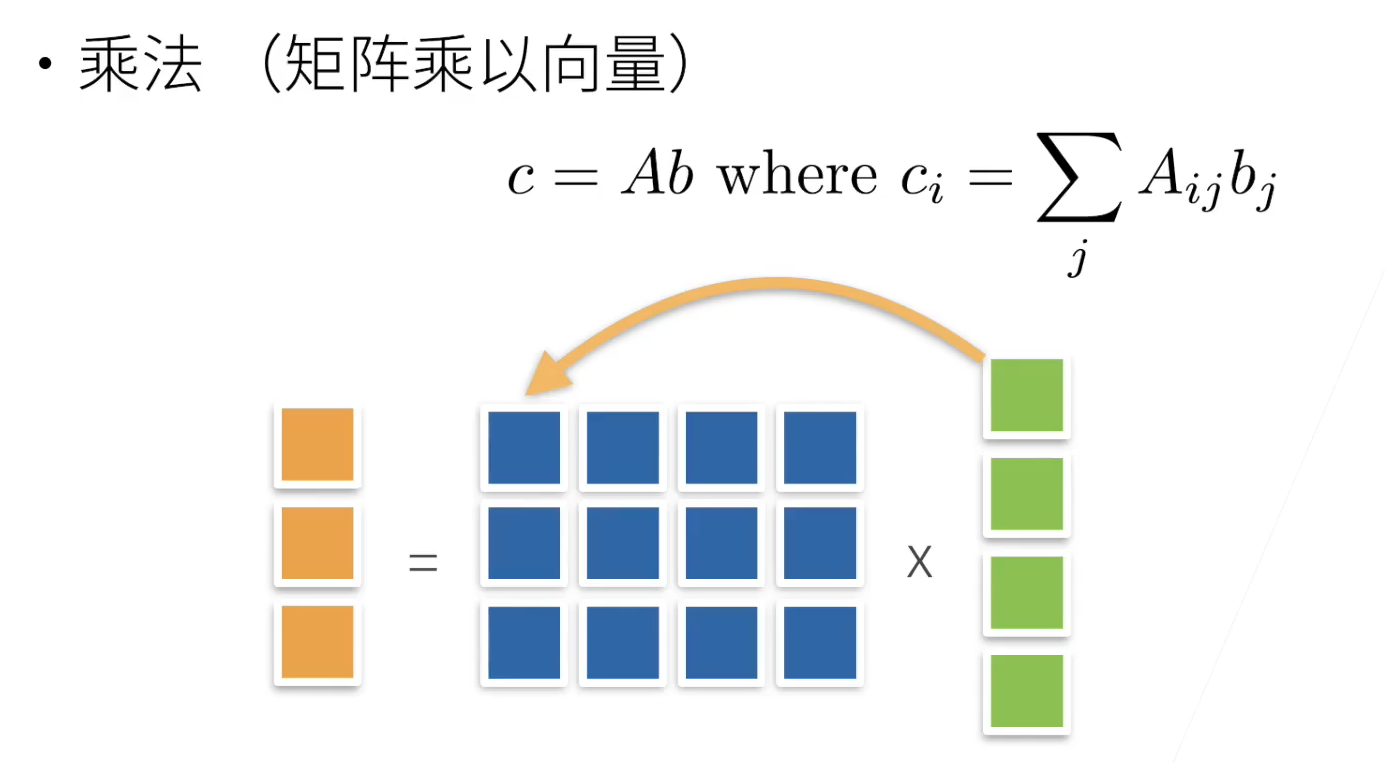
向量基本运算

线性代数的 Pytorch 写法

• 标量：torch.tensor([3.0])
• 向量：torch.tensor([list])
• 向量点积：torch.dot(x,y)，等价于先按元素乘，再求和：sum(x * y)
• 矩阵：torch.arange(20).reshape(5,4)
• 矩阵转置：A.T
• 两个矩阵按元素乘（哈达玛积，Hadamard product，数学符号为 ）[常用于CNN的卷积（互相关)运算中]：A * B
• 矩阵求和，得到标量：A.sum()
• 矩阵按轴求和，则该轴维度变为 1：A.sum(axis=n) | A.sum(axis=[a,b])

操作	被求和的维度	输入形状	输出形状	含义
A.sum(axis=0)	第0维	(2, 5, 4)	(5, 4)，上下两块加在一起	对两个5×4矩阵逐元素相加
A.sum(axis=1)	第1维	(2, 5, 4)	(2, 4)， 每层的 5 行相加成 1 行	每层的5行相加，保留列
A.sum(axis=2)	第2维	(2, 5, 4)	(2, 5)， 每行的 4 列相加成 1 个值	每层的4列相加，保留行

• 矩阵求和时保留维度信息：A.sum(axis=1,keepdims=True)
• 矩阵求均值：A.mean()
• 矩阵的累加：A.cumsum(axis=n)，必须要指定维度
• 矩阵向量积Ax，需保证矩阵列数与向量维数相等：torch.mv(A,x)
• 矩阵相乘AB，可以看作是执行 m 次矩阵向量积，并拼合结果：torch.mm(A,B)
• L2范数：torch.norm(u)
  • 
• L1范数：torch.abs(u).sum()
  • 
• 矩阵的 Frob 范数：torch.norm(A)
  • 

# 标量
# 标量由只有一个元素的张量表示
import torch
x=torch.tensor([3.0])
y=torch.tensor([2.0])
print(x+y)
print(x-y)
print(x/y)
print(x**y)输出：
tensor([5.])
tensor([6.])
tensor([1.5000])
tensor([9.])

# 向量
# 创建向量
x=torch.arange(4)   #tensor([0, 1, 2, 3])
# 访问向量元素
print(x[3])  #tensor(3)
# 访问向量的长度
print(len(x))   # 4
# 访问向量的维度
print(x.shape)  # torch.Size([4])

# 矩阵
# 创建
# 通过两个指定的分量m和n来创建m*n的矩阵
A=torch.arange(20).reshape(5,4)
print(A)输出：
tensor([[ 0,  1,  2,  3],[ 4,  5,  6,  7],[ 8,  9, 10, 11],[12, 13, 14, 15],[16, 17, 18, 19]])

# 矩阵的转置
print(A)
print(A.T)输出：
tensor([[ 0,  1,  2,  3],[ 4,  5,  6,  7],[ 8,  9, 10, 11],[12, 13, 14, 15],[16, 17, 18, 19]])
tensor([[ 0,  4,  8, 12, 16],[ 1,  5,  9, 13, 17],[ 2,  6, 10, 14, 18],[ 3,  7, 11, 15, 19]])

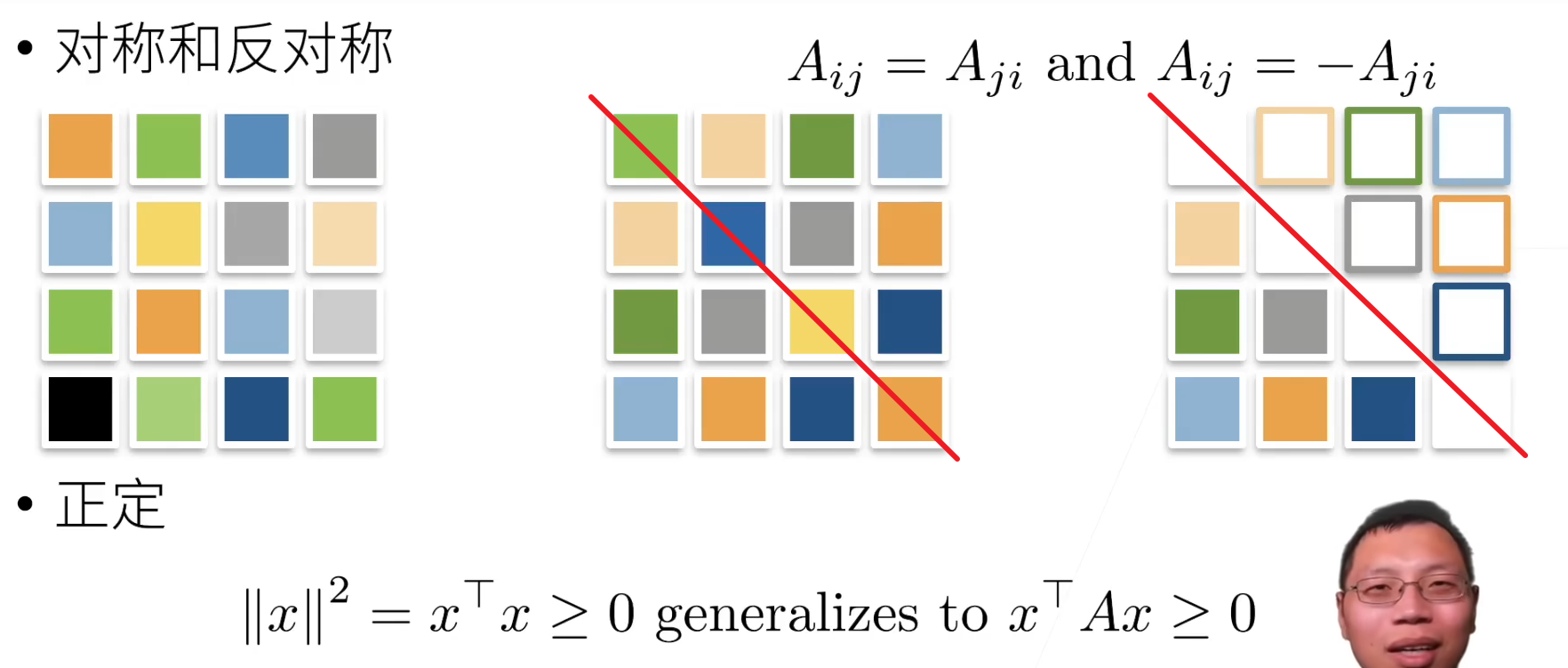
# 对称矩阵
# 对称矩阵A等于其转置A=A.T
B=torch.tensor([[1,2,3],[2,0,4],[3,4,5]])
print(B)
print(B.T)
print(B==B.T)

# 多维矩阵
X=torch.arange(24).reshape(2,3,4)
print(X)输出：
tensor([[[ 0,  1,  2,  3],[ 4,  5,  6,  7],[ 8,  9, 10, 11]],[[12, 13, 14, 15],[16, 17, 18, 19],[20, 21, 22, 23]]])

# 矩阵克隆
# 给定具有相同形状的任何两个张量，任何按元素二元运算的结果都将是相同形状的张量
A=torch.arange(20,dtype=torch.float32).reshape(5,4)
B=A.clone #通过分配新内存，将A的一个副本分配给B
print(A)
print(A+B)

# 矩阵相乘（对应元素相乘）
A = torch.arange(20,dtype=torch.float32).reshape(5,4)
B = A.clone() # 通过分配新内存，将A的一个副本分配给B
print(A)
print(A*B)

# 矩阵加标量
a=2
X=torch.arange(24).reshape(2,3,4)
print(a+X)
print((a*X).shape)

# 向量求和
X=torch.arange(4,dtype=torch.float32)
print(X)
print(X.sum())输出：
tensor([0., 1., 2., 3.])
tensor(6.)

# 矩阵求和
A=torch.arange(20*2).reshape(2,5,4)
print(A.shape)
print(A.sum())输出：
torch.Size([2, 5, 4])
tensor(780)

# 矩阵某轴求和（丢失维度）
# 指定张量沿哪一个和轴来通过求和降低维度
# 沿哪个维度计算就是消灭那一维度
# 构建原始矩阵
import torch
A=torch.arange(20*2).reshape(2,5,4)
print(A)输出：
tensor([[[ 0,  1,  2,  3],[ 4,  5,  6,  7],[ 8,  9, 10, 11],[12, 13, 14, 15],[16, 17, 18, 19]],[[20, 21, 22, 23],[24, 25, 26, 27],[28, 29, 30, 31],[32, 33, 34, 35],[36, 37, 38, 39]]])

A_sum_axis0=A.sum(axis=0) #(2,5,4) 对第一个维度进行求和，剩下两个维度留下来了
print(A_sum_axis0)
print(A_sum_axis0.shape)输出：
tensor([[20, 22, 24, 26],[28, 30, 32, 34],[36, 38, 40, 42],[44, 46, 48, 50],[52, 54, 56, 58]])
torch.Size([5, 4])

A_sum_axis1=A.sum(axis=1)  # (2,5,4) 对第二个维度进行求和，剩下两个维度留下来了
print(A_sum_axis1)
print(A_sum_axis1.shape)输出：
tensor([[ 40,  45,  50,  55],[140, 145, 150, 155]])
torch.Size([2, 4])

A_sum_axis2=A.sum([0,1])
print(A_sum_axis2)
print(A_sum_axis2.shape)输出：
tensor([180, 190, 200, 210])
torch.Size([4])

# 矩阵平均值
# 一个与求和相关的量是平均值（mean或average）
import torch
A=torch.arange(20,dtype=torch.float32).reshape(5,4)
print(A.mean())
# 张量A中有多少个元素
print(A.numel())
print(A.sum()/A.numel())输出：
tensor(9.5000)
20
tensor(9.5000)# 沿着某一维度求平均值
# 沿着第0维（行方向）求平均
# 也就是对每一列求平均
print(A.mean(axis=0))
print(A.sum(axis=0))
print(A.shape[0])
print(A.sum(axis=0)/A.shape[0])输出：
tensor([ 8.,  9., 10., 11.])
tensor([40., 45., 50., 55.])
5
tensor([ 8.,  9., 10., 11.])

# 矩阵某轴求和（不丢失维度）
# 计算总和或均值时保持轴数不变
import torch
A=torch.arange(20,dtype=torch.float32).reshape(5,4)
# keepdims=True不丢掉维度，否则三维矩阵按一个维度求和就会变为二维矩阵
# 二维矩阵若按一个维度求和就会变为一维向量
sum_A=A.sum(axis=1,keepdims=True)  
print(sum_A)
print(sum_A.shape)  #维度没丢失，方便使用广播输出：
tensor([[ 6.],[22.],[38.],[54.],[70.]])
torch.Size([5, 1])

# 矩阵广播
# 通过广播将A除以sum_A
import torch
A=torch.arange(20,dtype=torch.float32).reshape(5,4)
sum_A=A.sum(axis=1, keepdims=True)
print(A/sum_A)输出：
tensor([[0.0000, 0.1667, 0.3333, 0.5000],[0.1818, 0.2273, 0.2727, 0.3182],[0.2105, 0.2368, 0.2632, 0.2895],[0.2222, 0.2407, 0.2593, 0.2778],[0.2286, 0.2429, 0.2571, 0.2714]])

# 矩阵某轴累积
import torch
A=torch.arange(20,dtype=torch.float32).reshape(5,4)
print(A.cumsum(axis=0))输出：
tensor([[ 0.,  1.,  2.,  3.],[ 4.,  6.,  8., 10.],[12., 15., 18., 21.],[24., 28., 32., 36.],[40., 45., 50., 55.]])

详解过程：
A =                              
[[ 0.,  1.,  2.,  3.],        [ 4.,  5.,  6.,  7.],         [ 8.,  9., 10., 11.],      [12., 13., 14., 15.],             [16., 17., 18., 19.]]           
变成了
A.cumsum(axis=0) =
tensor([[ 0.,  1.,  2.,  3.],[ 4.,  6.,  8., 10.],[12., 15., 18., 21.],[24., 28., 32., 36.],[40., 45., 50., 55.]])

# 向量点积
# 点积是相同位置的按元素乘积的和
import torch
x=torch.arange(4,dtype=torch.float32)
y=torch.ones(4,dtype=torch.float32)
print(x)
print(y)
print(torch.dot(x,y))输出：
tensor([0., 1., 2., 3.])
tensor([1., 1., 1., 1.])
tensor(6.)# 可以通过执行按元素乘法，然后进行求和来表示两个向量的点积
import torch
x=torch.arange(4,dtype=torch.float32)
y=torch.ones(4,dtype=torch.float32)
print(torch.sum(x*y))输出：
tensor(6.)

# 矩阵向量积（每行点积）
# A是一个m×n的矩阵，x是一个n×1的矩阵，矩阵向量积Ax是一个长度为m的列向量，其第i个元素是点积aᵢᵀx。
import torch
A=torch.arange(20,dtype=torch.float32).reshape(5,4)
x=torch.arange(4,dtype=torch.float32)
print(A.shape)
print(x.shape)
print(torch.mv(A,x))输出：
torch.Size([5, 4])
torch.Size([4])
tensor([ 14.,  38.,  62.,  86., 110.])

矩阵向量积的计算过程
A =                           x = [0., 1., 2., 3.]
[[ 0.,  1.,  2.,  3.],[ 4.,  5.,  6.,  7.],[ 8.,  9., 10., 11.],[12., 13., 14., 15.],[16., 17., 18., 19.]]
将一个形状为 (m, n) 的矩阵 A与一个形状为 (n,) 的向量 x 相乘，得到一个形状为 (m,) 的向量。
第一行：[0,1,2,3] · [0,1,2,3] = 0*0 + 1*1 + 2*2 + 3*3 = 14
第二行：[4,5,6,7] · [0,1,2,3] = 4*0 + 5*1 + 6*2 + 7*3 = 5 + 12 + 21 = 38

# 矩阵相乘（线性代数相乘）
# 可以将矩阵-矩阵乘法AB看作是简单地执行m次矩阵-向量积，并将结果拼接在一起，形成一个n×m矩阵。
import torch
A=torch.arange(20,dtype=torch.float32).reshape(5,4)
B=torch.ones(4,3)
print(A)
print(B)
print(torch.mm(A,B))输出：
tensor([[ 0.,  1.,  2.,  3.],[ 4.,  5.,  6.,  7.],[ 8.,  9., 10., 11.],[12., 13., 14., 15.],[16., 17., 18., 19.]])
tensor([[1., 1., 1.],[1., 1., 1.],[1., 1., 1.],[1., 1., 1.]])
tensor([[ 6.,  6.,  6.],[22., 22., 22.],[38., 38., 38.],[54., 54., 54.],[70., 70., 70.]])

# 矩阵L2范数
import torch
u=torch.tensor([3.0,-4.0])
print(torch.norm(u))输出：
tensor(5.)

# 矩阵L1范数
u=torch.tensor([3.0,-4.0])
print(torch.abs(u).sum())输出：
tensor(7.)

# 矩阵F范数
print(torch.norm(torch.ones((4,9)))) # 把矩阵拉成一个向量，然后再求和输出：
tensor(6.)

Q&A

Q：怎么改变 Tensor 里元素的数据类型：int/float？

A：首先介绍 Pytorch8 种张量类型：

• torch.FloatTensor：32bit 精度浮点张量 [Pytorch 默认类型] dtype 值为：torch.float32 or torch.float
• torch.DoubleTensor：64bit 精度浮点张量，dtype 值为：torch.float64 or torch.double （深度学习用的较少，因为计算、存储成本太大）
• torch.HalfTensor：半精度（16bit）浮点张量，dtype 值为：torch.float16 or torch.half
• torch.ByteTensor：8bit 无符号整型张量，dtype 值为：torch.uint8（深度学习领域鲜有使用）
• torch.CharTensor：8bit 字符型张量，dtype 值为：torch.int8
• torch.ShortTensor：16bit 短整型张量，dtype 值为：torch.int16 or torch.short（深度学习领域鲜有使用）
• torch.IntTensor：32bit 整型张量，dtype 值为：torch.int32 or torch.int（深度学习领域鲜有使用）
• torch.LongTensor：64bit 长整型张量，dtype 值为：torch.int64 or torch.long（深度学习领域鲜有使用）

要查看已有张量的类型，可通过在张量后使用属性：.dtype查看

怎样改变数据类型：

• 第一种方法： 在构建时直接指定上面提到的 8 种类型：
  • torch.IntTensor([[1,2],[3,4]])或torch.tensor([1,2,3],dtype=torch.long)
• 第二种方法： 使用.type()方法转换已有张量的类型：
  • tensor1.type(torch.HalfTensor)

具体可参考Pytorch文档

3.矩阵运算

关于微积分相关知识，继续强烈推荐3Blue1Brown的超棒教程 👇

矩阵求导的意义

在深度学习里，本质是非凸参数优化问题，例如数据的特征化、损失函数和优化算法的选择，都是将原本不可导的问题转换为可导的目标，进而通过数据迭代计算梯度，再沿梯度反方向微调参数，直至结果收敛在一个合适的区间。

标量导数

亚导数

求导

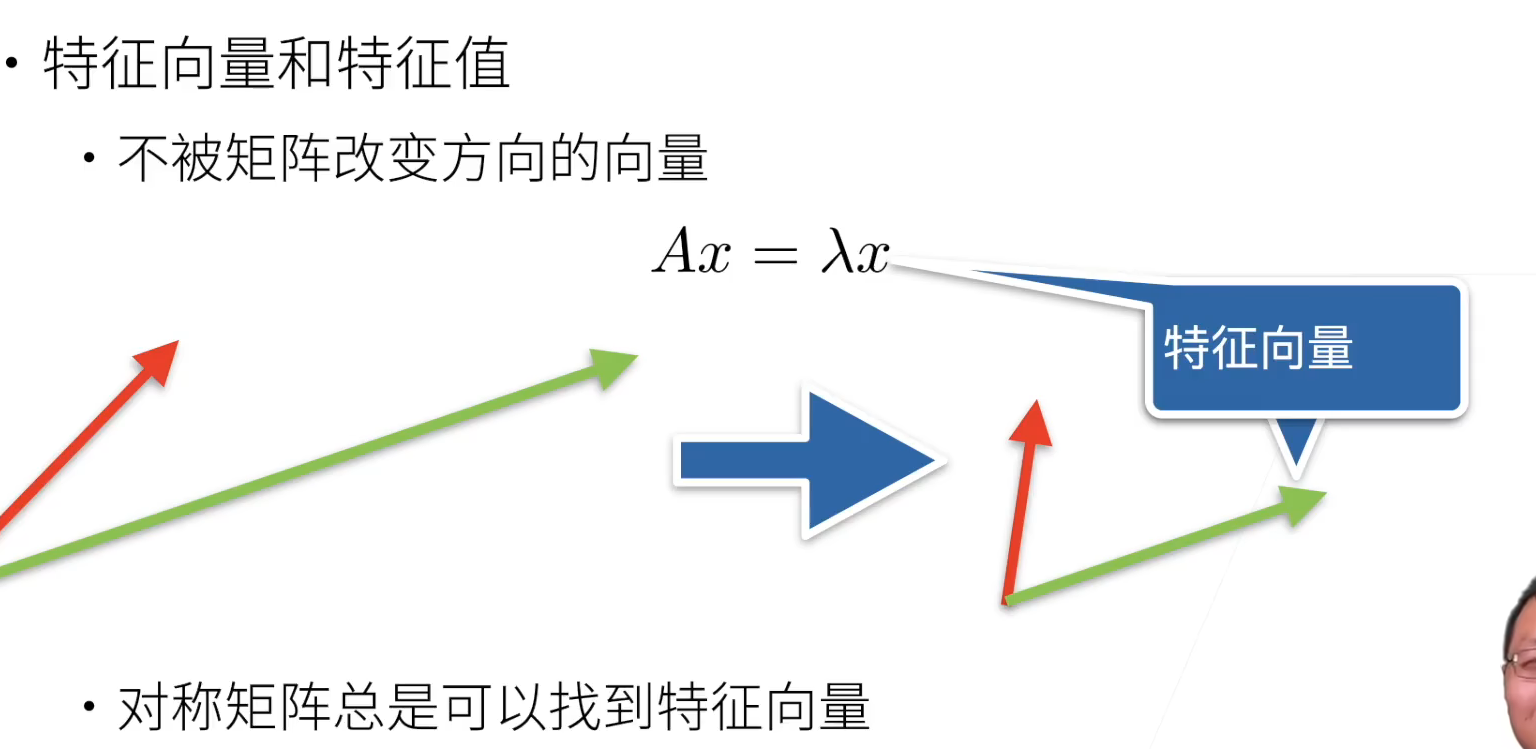
梯度

因变量 (y)	自变量 (x)	结果类型	名称
标量	标量	标量	普通导数
向量	标量	向量	向量导数（每个分量对标量求导）
标量	向量	向量	梯度（Gradient）
向量	向量	矩阵（m×n）	雅可比矩阵（Jacobian）

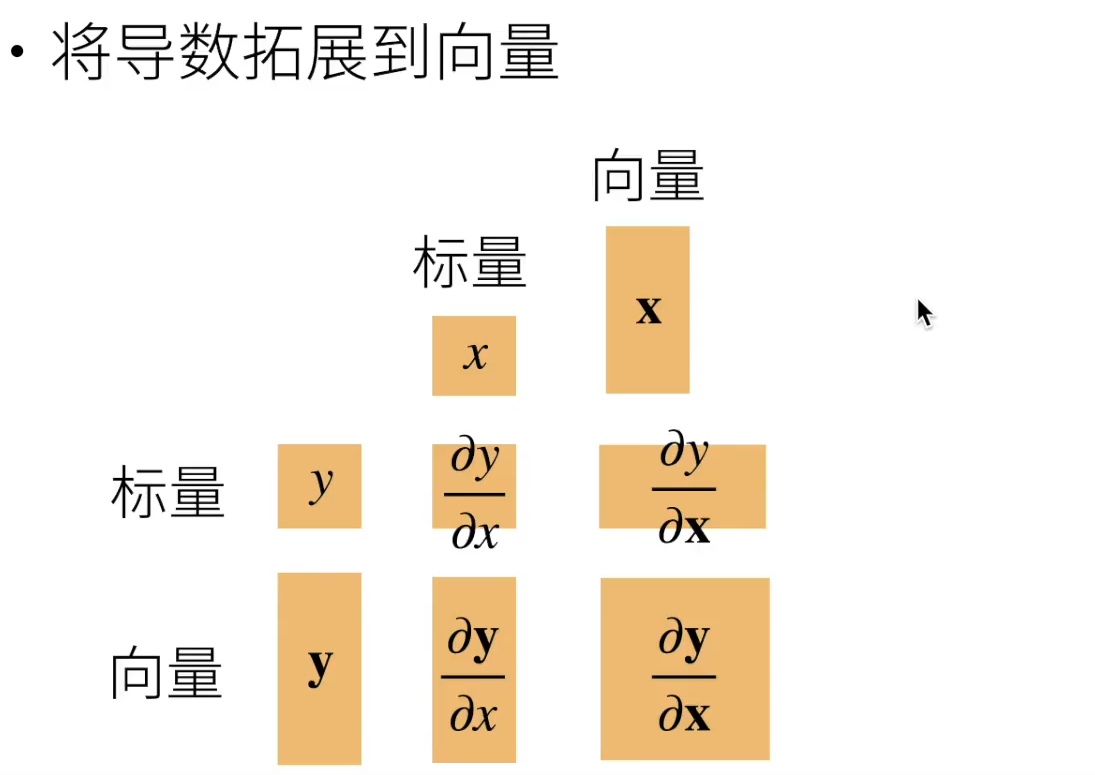
标量对向量求导

举个例子：

是一个椭圆，梯度是指向值变化最大的方向

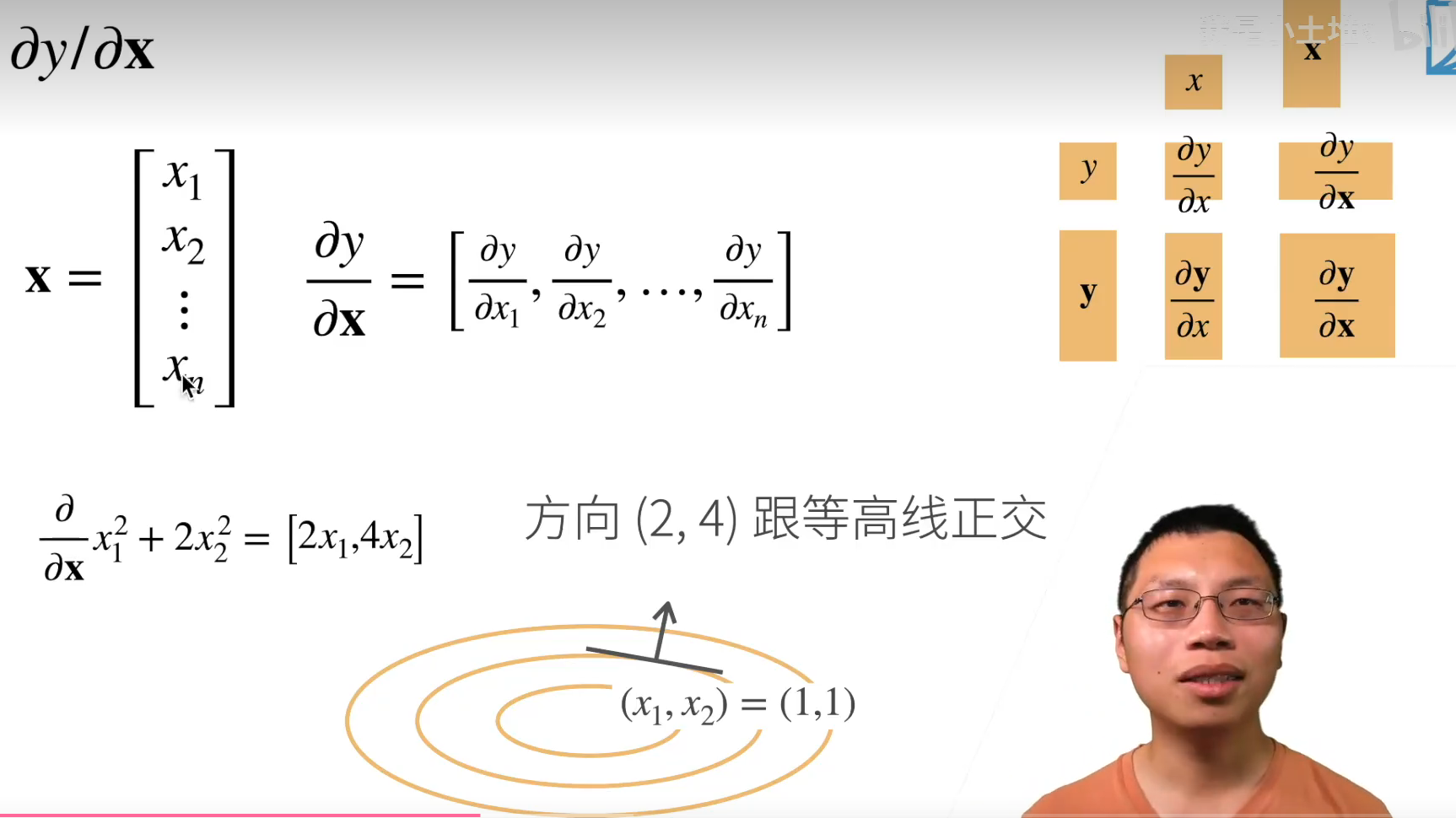
样例：

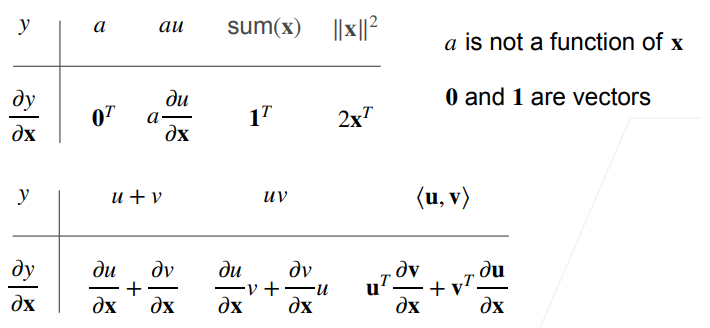
应用到深度学习------梯度

向量对标量求导

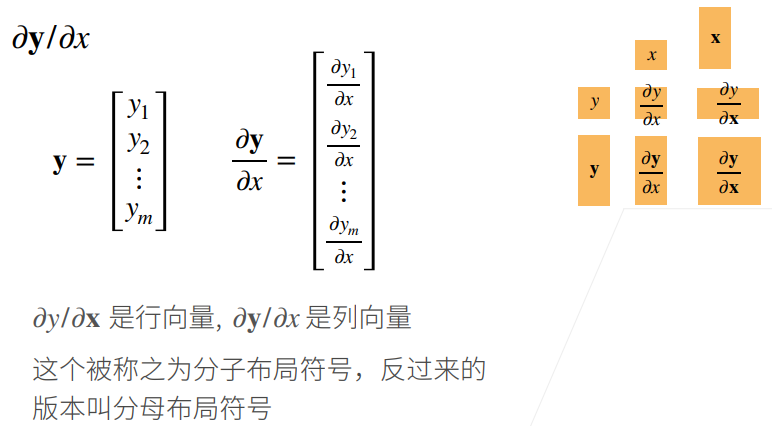
向量对向量求导

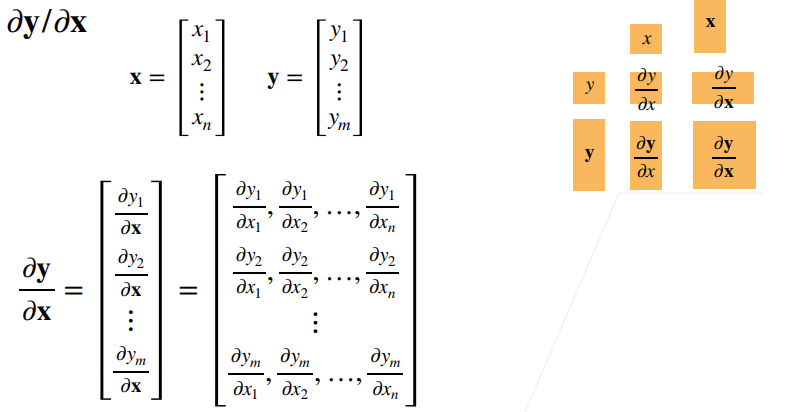
样例：

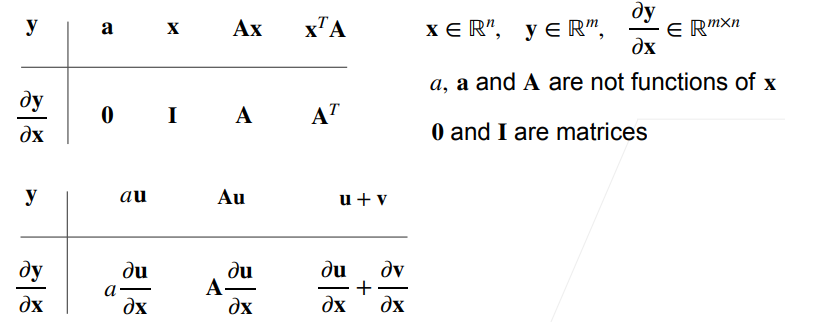
扩展：矩阵对矩阵的求导

4.自动求导

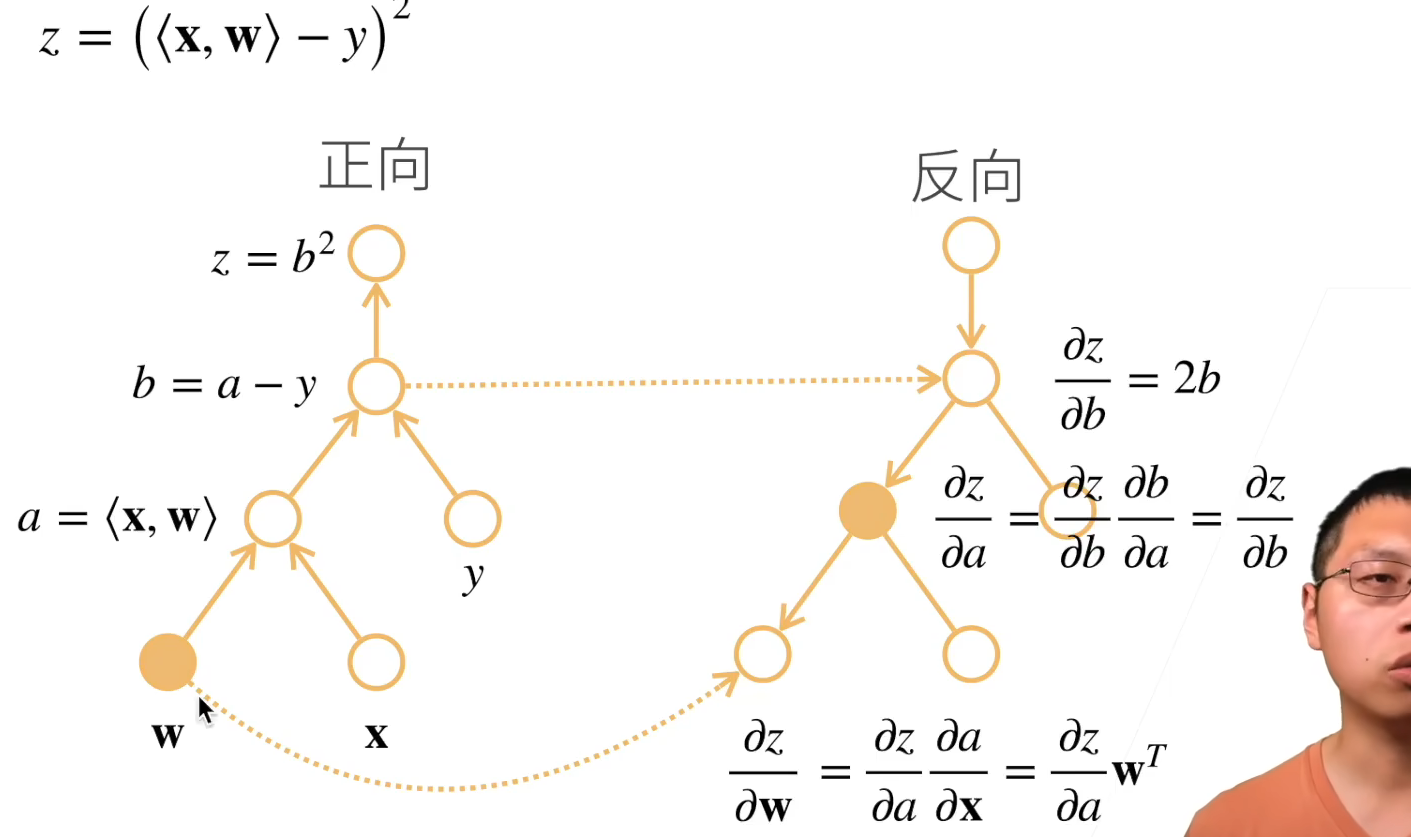
向量求导的链式法则

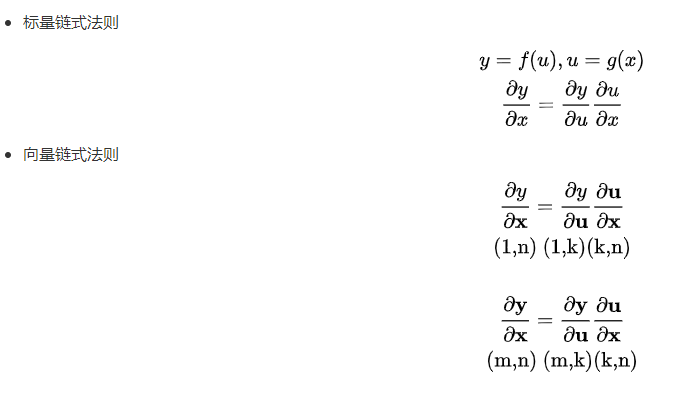
• 向量链式法则求导示例：

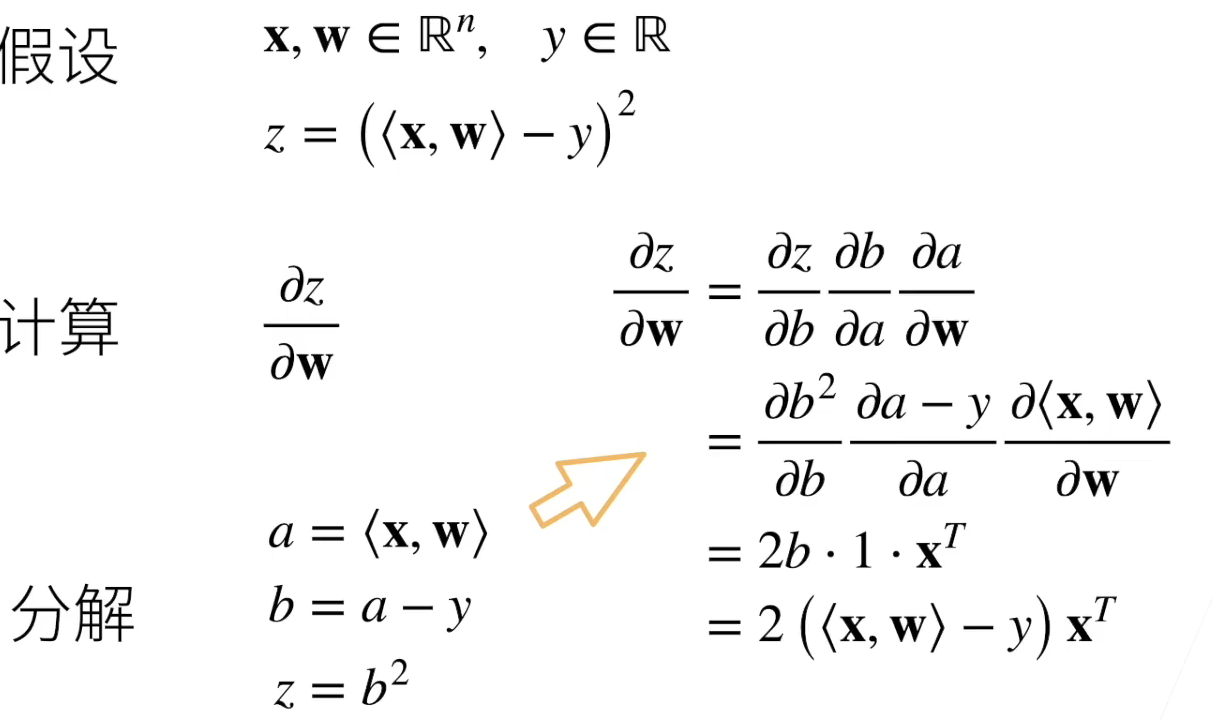
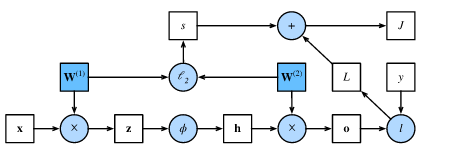
详解：

• 矩阵链式法则求导示例

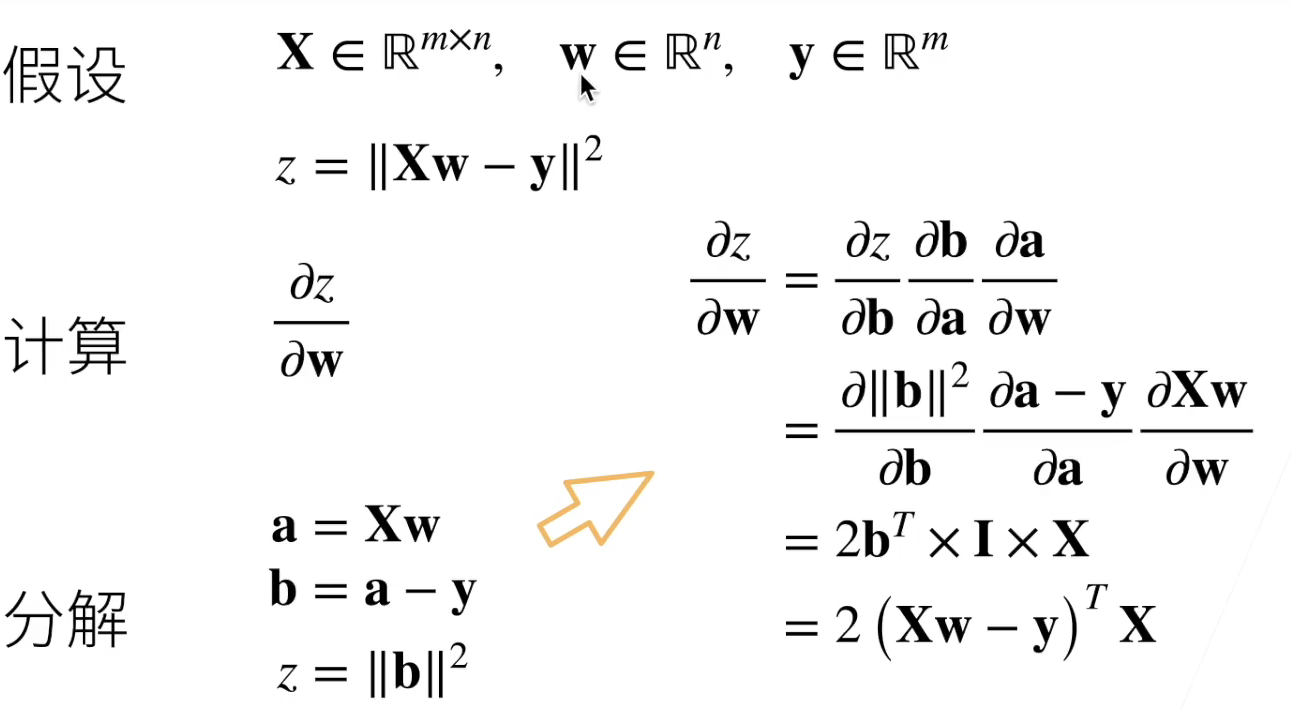
自动求导

自动求导计算一个函数在指定值上的导数

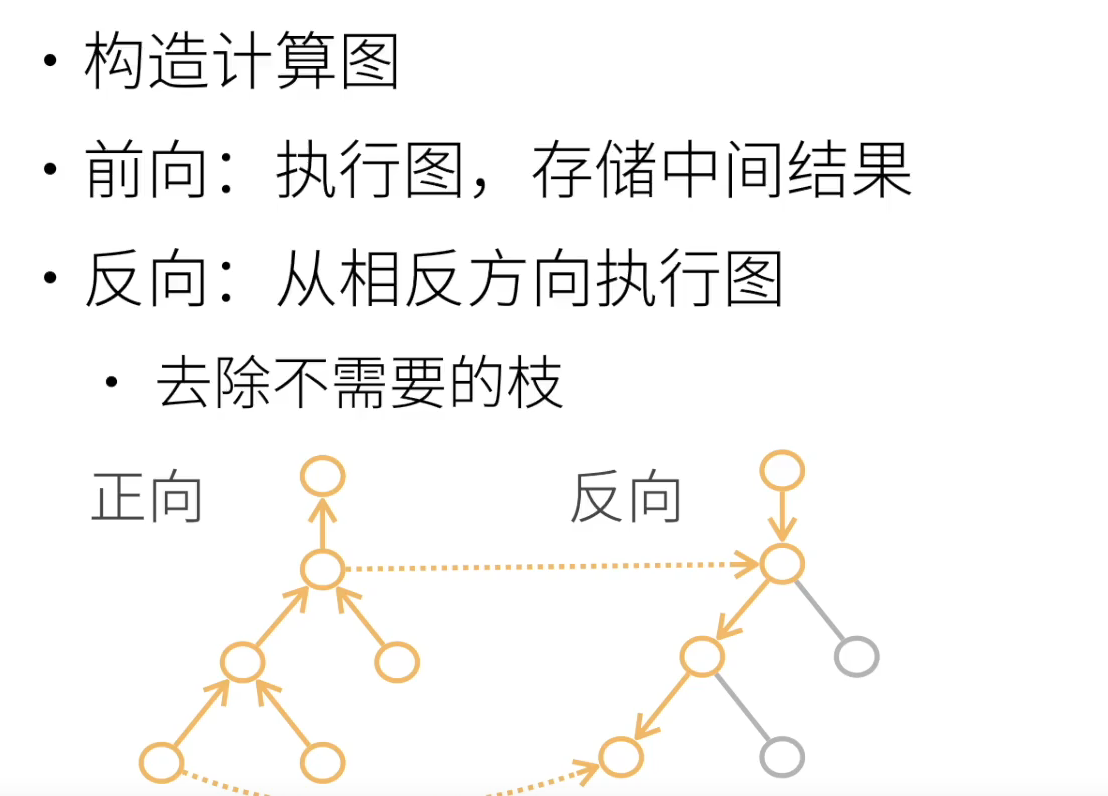
计算图

可以理解为是一张记录计算过程的“流程图”,计算图帮助pytorch实现自动求导

• 把代码分解成操作子
• 把计算表示成一个无环图

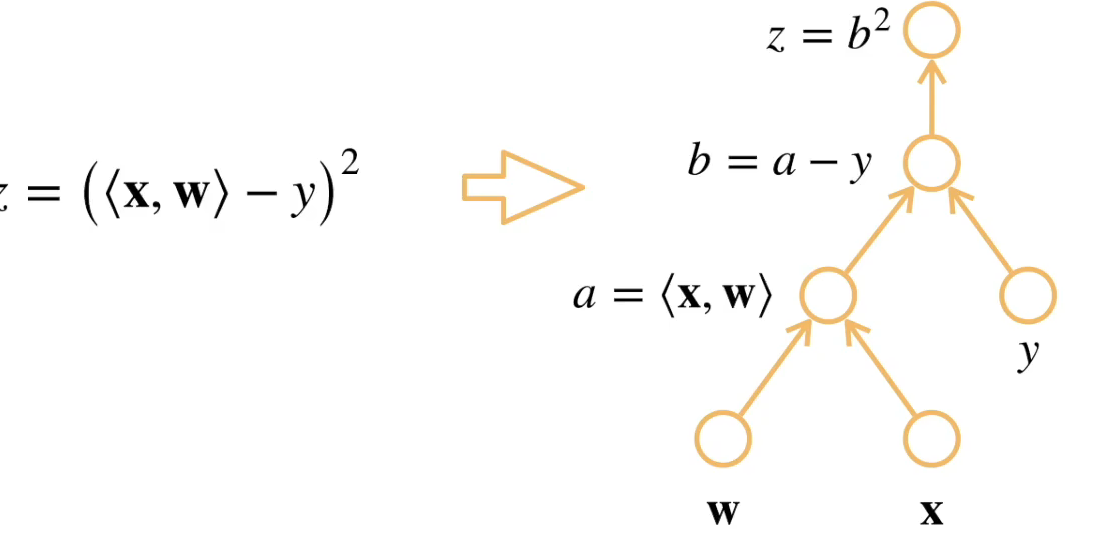
• 显式构造
  • Tensorflow/Theano/MXNet

• 隐式构造
  • PyTorch/MXNet

计算图是几乎目前所有深度学习框架使用的、用于实现神经网络计算的底层模型，是将复杂运算拆分成由多个简单运算符（操作子）组成的有向无环图（DAG, Directed Acyclic Graph）👉Wiki，可以实现自动求导（正向传播、反向传播 Backpropagation👉Wiki）功能。

关于反向传播算法，推荐观看3Blue1Brown博主的科普视频👇

使用计算图模型，可更方便的进行并行化运算（惰性求值），同时拆分成简单的运算符，可充分利用专有硬件（如 GPU 等）实现硬件加速来提升计算效率，详细内容可参考👉这里

正向传播复杂度：

• 计算复杂度为O(n)，n 代表计算图中操作子数目
• 内存复杂度为O(1)，1 表示每次计算只用存储当前操作子的数据，计算下一操作时便可释放前一个中间结果，所以为常量复杂度

反向传播复杂度：

• 计算复杂度为O(n)，与正向复杂度类似
• 内存复杂度为O(n)，因为计算反向梯度时，需要所有操作子正向传播的中间结果

以上复杂度也决定了当神经网络非常大时，在训练过程中，对内存（CPU 计算）或显存（GPU 计算）容量要求非常高，因为所消耗的容量正比于神经网络节点数。

关于计算图相关知识，李沐的视频教程较为简略，可参考官方文档中的文字讲解 👉点击这里，同时还可观看吴恩达(AndrewNG)的 DeepLearning.ai 课程中的《计算图》章节

自动求导的两种模式

反向积累总结：

复杂度

自动求导代码实现

目前几乎所有的深度学习框架（Pytorch、TensorFlow、MXNet etc.）可通过自动计算导数，即自动微分（automatic differentiation）来加快求导。

实际中，根据我们设计的模型，系统会构建一个计算图（computational graph）， 来跟踪计算是哪些数据通过哪些操作组合起来产生输出。 自动微分使系统能够随后反向传播梯度。 这里，反向传播（backpropagate）意味着跟踪整个计算图，填充关于每个参数的偏导数。

• tensor1.requires_grad_(True)：告诉框架需要对**该张量**求导
• tensor2.backward()：求 tensor2 对 tensor1 导数（tensor2 需为 tensor1 的表达式，且求导前要执行requires_grad_(True)命令）
• tensor1.grad：访问求导后张量的导数
• tensor.grad.zero_()：梯度清零（Pytorch 默认会累计梯度并存储在.grad内）
• tensor.detach()：将该变量移出计算图，当作常量处理，多用于神经网络的参数固定
• 一般很少用到向量对向量（以及更高阶）的求导，需要引入一个 gradient 参数，所以会把一个向量转化为标量求导，最常用的就是求和：tensor.sum().backward()。loss一般是一个标量，如果 loss 是矩阵，维度就会越算越大。
• 可以经过 Python 计算流再求导。

代码实现：

假设想对函数关于列向量x求导。

import torch
x=torch.arange(4)
x输出：
tensor([0., 1., 2., 3.])

# 在外面计算y关于x的梯度之前，需要一个地方来存储梯度。
# 告诉 PyTorch：这个张量 x 需要被追踪梯度（grad）
x.requires_grad_(True)  ## 等价于 x = torch.arange(4.0,requires_grad=True)
print(x.grad)   #默认为None输出：
None

# 计算y
x = torch.arange(4.0,requires_grad=True)
y=2*torch.dot(x,x)
# grad_fn是隐式的构造了梯度函数，代表当前这个张量是由哪个运算产生的，以及它在反向传播时该怎么求导
print(y)   输出：
tensor(28., grad_fn=<MulBackward0>)

# 通过调用反向传播函数来自动计算y关于x每个分量的梯度
y.backward()    # 反向传播后会有梯度计算出来
print(x.grad)   #访问导数，即访问梯度
print(x.grad==4*x)  #4*x是2*x*x的导数输出：
tensor([ 0.,  4.,  8., 12.])
tensor([True, True, True, True])

# 计算x的另一个函数
y.backward()
# 默认情况下，PyTorch会累积梯度，需要清除之前的值
x.grad.zero()  # y.backward() 后才能产生梯度，才能梯度清零，没有反向传播，无法梯度清零
y=x.sum()  ## 这里的y是一个标量，sum函数其实就是x_1+x_2+...x_n，求偏导自然是全1啊
y.backward()
print(x.grad)输出：
tensor([1., 1., 1., 1.])

# 在深度学习中，目的不是计算微分矩阵，而是批量中每个样本单独计算的偏导数之和。
import torch
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x,x)
y.backward()
# 默认情况下，PyTorch会累积梯度，需要清除之前的值
# 对非标量调用 'backward' 需要传入一个 'gradient' 参数，该参数指定微分函数
x.grad.zero_()y=x*x  ## 这里的y不是一个标量，这是一个向量
print(y)  # 输出tensor([0., 1., 4., 9.], grad_fn=<MulBackward0>)
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()  # y.sum()后就将向量转为标量了，对标量求导
x.grad输出：
tensor([0., 2., 4., 6.])

默认情况下，PyTorch 会沿着计算图，从输出往回一路传播梯度。
但有时候我们只想让一部分参数更新，另一部分不更新或当常量看待。

.detach() 的作用是：“让某个中间变量从计算图中脱离，不再对之前的张量求梯度。”

# 将某些计算移动到计算图之外
import torch
# 创建变量并开启梯度追踪
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x,x)
y.backward()
x.grad.zero_()y=x*x
# 结果表明这个 y 是从 x 计算得到的，仍然在计算图里，会被 autograd 跟踪
print(y)  #tensor([0., 1., 4., 9.], grad_fn=<MulBackward0>)# 使用.detach()切断计算图
# .detach() 会生成一个新的张量 u，内容与 y 一样，但不再与计算图绑定。
u=y.detach() # y.detach把y当作一个常数，而不是关于x的一个函数
print(y.detach())  # tensor([0., 1., 4., 9.])
print(u)     #tensor([0., 1., 4., 9.])z=u*x
z.sum().backward()
x.grad==u   # tensor([True, True, True, True])

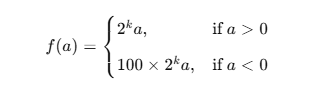
#即使构建函数的计算图需要通过Python控制流（例如，条件、循环或任意函数调用），仍然可以计算得到变量的梯度。
# 即使 f(a) 包含循环和条件判断，PyTorch 仍然能自动追踪运算路径并正确求导
def f(a):b=a*2# 不断把 b 翻倍,直到 b 的绝对值（L2范数） ≥ 1000 为止。while b.norm()<1000:   #norm是L2范数b=b*2if b.sum()>0:c=belse:c=100*breturn c
a=torch.randn(size=(),requires_grad=True)
print(a)  #tensor(-0.5028, requires_grad=True)
d=f(a)
d.backward()
print(a.grad)  #tensor(204800.)
print(d/a)  # tensor(204800., grad_fn=<DivBackward0>)# d是a的线性函数，所以导数就是斜率d/a
a.grad==d/a   #tensor(True)

总结：

• 只能对标量调用 backward()（否则要传梯度参数）
• 梯度会累加，所以常用 zero_() 清空
• detach() 切断梯度，不等于拷贝值，只是不再求导
• 默认动态图机制：每次执行都会重新建图
• 内存释放机制：backward() 默认销毁计算图，要重复用可加参数 retain_graph=True

PyTorch 的自动求导系统通过 动态计算图 自动追踪所有张量的运算

1. 设置 requires_grad=True，
2. 正常计算前向过程，
3. 调用 .backward()，
   PyTorch 就能自动完成反向传播，计算出每个变量的梯度。

同时可以用 .detach() 控制梯度流向，实现灵活的模型训练与优化。

5.线性回归

在机器学习领域，大致可分为回归与分类两类问题。

回归是指一类为一个或多个自变量与因变量之间关系建模的方法。在自然科学和社会科学领域，回归经常用来表示输入和输出之间的关系；在现实生活中，回归常用于解决预测问题

线性回归（Linear Regression）是最简单的一种回归模型，在对结果精度要求不高、现实情况相对不复杂的情况（假设满足线性关系），使用线性回归可以简便快速地得到可接受的结果

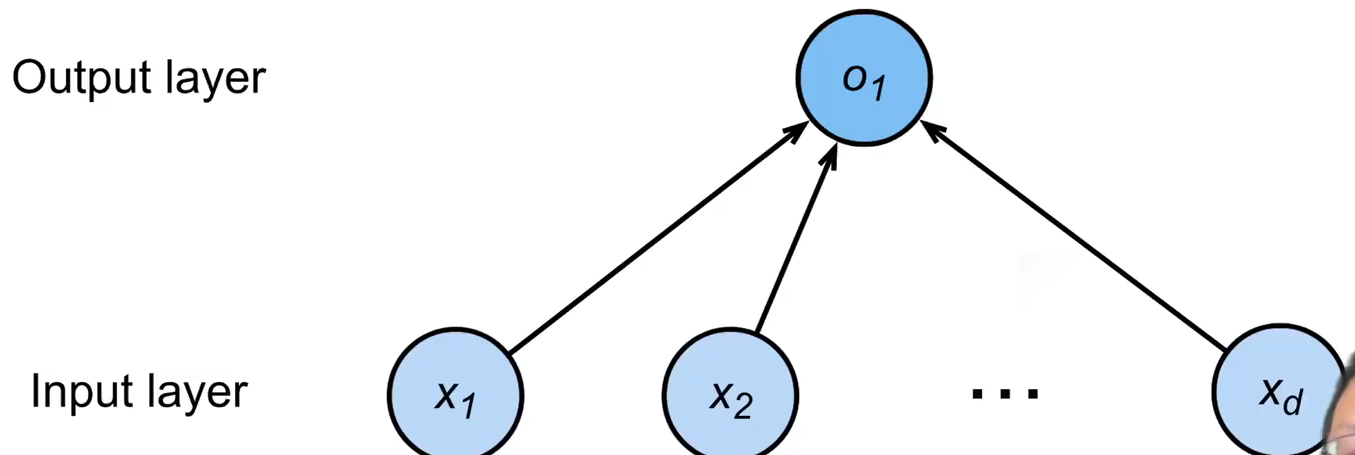
线性回归模型可以看作是激活函数为线性函数的单层神经网络模型。其中输入层节点数量等于数据特征个数：

房价预测

衡量预测的质量-----损失函数

训练数据

参数学习

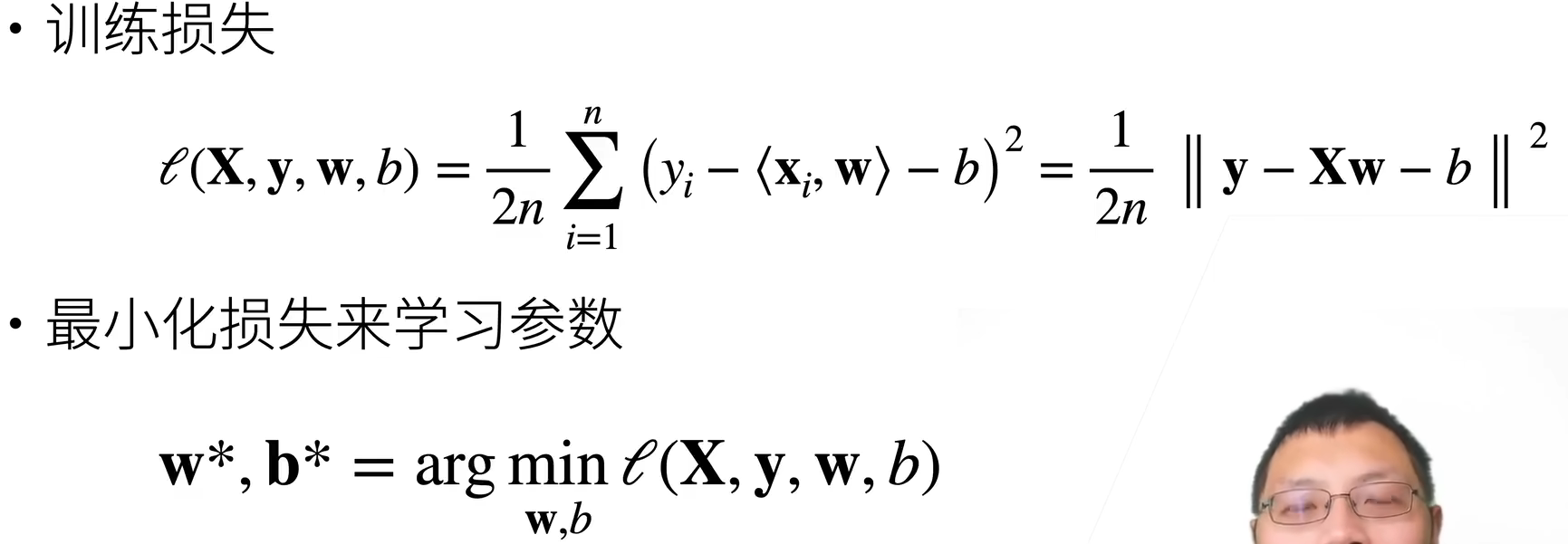
显示解：

总结：

• 线性回归是对n维输入的加权，外加偏差、
• 使用平方损失来衡量预测值和真实值的差异
• 线性回归有显示解
• 线性回归可以看作是单层神经网络

优化方法

梯度下降

如果一个模型没有显式解，就需要借助数值方法。

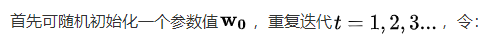
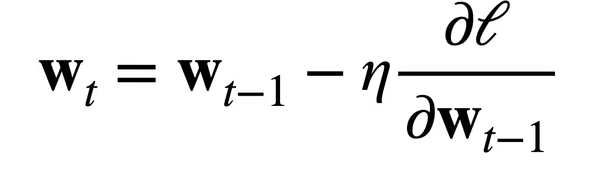
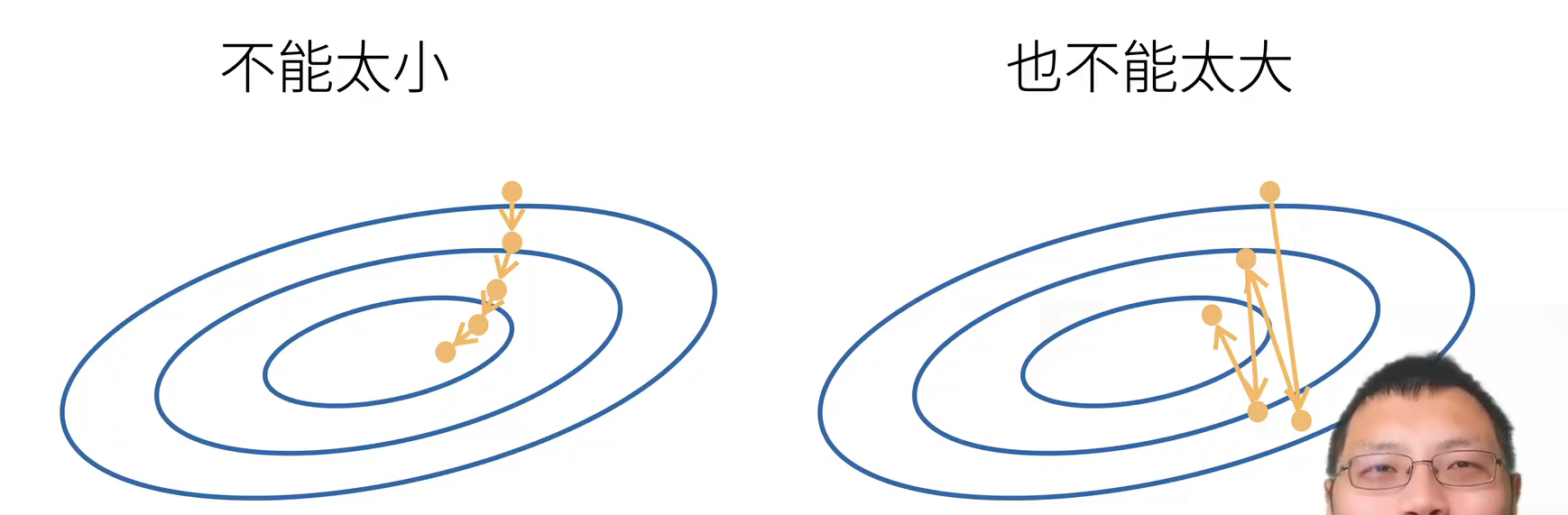
其中，学习率（）：步长的超参数（hyperparameter）,不能太小（会导致收敛时间过慢）也不能太大（产生震荡，无法收敛)

以此沿负梯度方向不断减小损失函数值。梯度下降就是不断延着负梯度方向更新求解，不需要求解显式解的形式，只要可导即可

小批量随机梯度下降法 (SGD)

在整个训练集上算梯度实在太贵
可以随机采样b个样本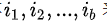来近似损失

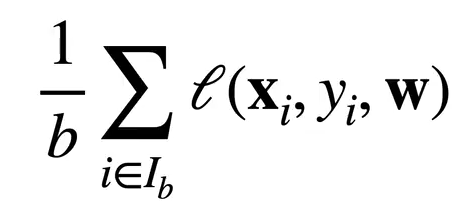
b为批量大小（batch），另外一个重要的超参数。为最大化计算效率，一般与运算设备（如 GPU)的存储大小相关，如 256、512、2048……

不能太小，不然每次计算量太小，不适合并行来最大利用计算资源

不能太小：内存消耗增加，浪费计算，例如如果所有样本都是相同的

梯度下降法通过不断沿着反梯度方向更新参数求解

小批量随机梯度下降法是深度学习默认的求解算法

2个重要的超参数是批量大小和学习率

线性回归的从零开始实现

• 以线性噪声为例

数学符号	代码变量	含义
( X )	features	特征矩阵，每行一个样本，每列一个特征
( y )	labels	标签（输出），与每个样本对应的真实值
( w, b )	true_w, true_b	真实权重和偏置，用来生成数据
噪声	torch.normal(0,0.01,y.shape)	模拟真实测量误差

%matplotlib inline
import random
import torch
from d2l import torch as d2ldef synthetic_data(w,b,num_exaples):"""生成 y = Xw + b + 噪声"""# 生成特征矩阵 X：num_examples 行，每行一个样本# 每个特征从标准正态分布 N(0,1) 中采样X = torch.normal(0,1,(num_exaples,len(w)))print("X.shape:",X.shape)# 按线性模型计算“无噪声的标签”y = torch.matmul(X,w) + bprint("y.shape:",y.shape)# 给 y 原地加上均值 0、标准差 0.01 的高斯噪声，模拟观测误差y += torch.normal(0,0.01,y.shape)print("y.shape:",y.shape)# 返回特征 X 和列向量形式的标签 yreturn X, y.reshape((-1,1))true_w = torch.tensor([2,-3.4])  # 真实权重
true_b = 4.2   # 真实偏置
# 一共生成 1000 个样本（num_examples=1000），每个样本 2 个特征（len(w)=2）
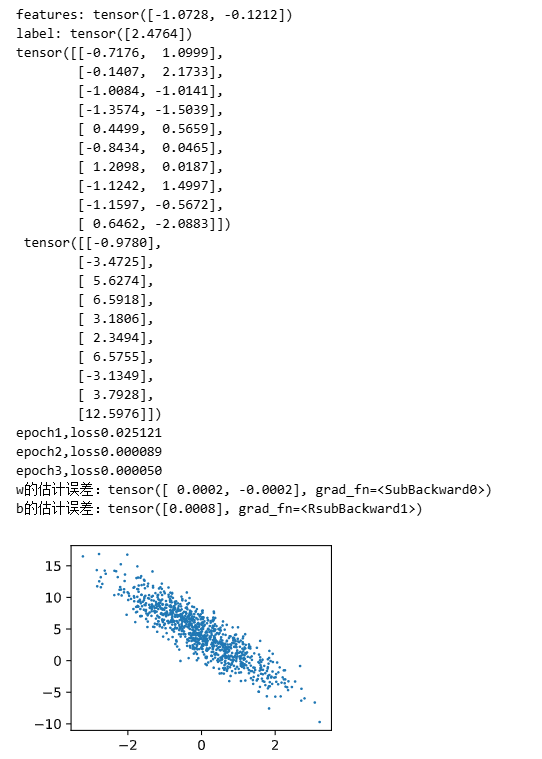
features, labels = synthetic_data(true_w, true_b, 1000)
# features 是一个 1000 × 2 的矩阵
print("features.shape:",features.shape)
# labels 是一个 1000 × 1 的列向量
print("labels.shape:",labels.shape)

# 绘制数据集
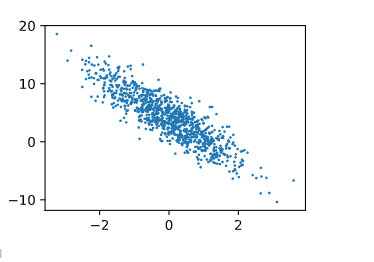
# features中每一行都包含一个二维数据样本，labels中的每一行都包含一维标签值（一个标签）
print('features:',features[0],'\nlabels[0]')
d2l.set_figsie()
# 只有detach后才能转到numpy里面去     
d2l.plt.scatter(features[:,1].detach().numpy(),labels.detach().numpy(),1)  # features取第2列输出：
features: tensor([ 0.7316, -2.4956]) 
label: tensor([14.1394])

# 读取小批量
# data_iter函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量
def data_iter(batch_size,features,labels):num_examples = len(features)  # 样本个数indices = list(range(num_examples)) # 样本索引# 这些样本是随即读取的，没有特定的顺序random.shuffle(indices) # 把索引随即打乱for i in range(0, num_examples, batch_size):batch_indices = torch.tensor(indices[i:min(i+batch_size,num_examples)]) # 当i+batch_size超出时，取num_examples         yield features[batch_indices], labels[batch_indices] # 获得随即顺序的特征，及对应的标签batch_size = 10
for X,y in data_iter(batch_size, features, labels):print(X, '\n', y) # 取一个批次后，就break跳出了break

data_iter 函数：

这个函数是一个 生成器（generator），
它每次会返回一个“小批量数据（mini-batch）”，用于训练时的梯度更新。

• batch_size=10 → 每次取10条样本；
• random.shuffle → 打乱样本顺序（避免模型总看到同样的数据顺序）；
• yield → 每次返回一个批次的 (X, y)；
• 外部可以用 for X, y in data_iter(...): 逐批取出数据。

完整模型：

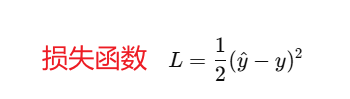
%matplotlib inline
import random
import torch
from d2l import torch as d2ldef synthetic_data(w,b,num_exaples):"""生成 y = Xw + b + 噪声"""X = torch.normal(0,1,(num_exaples,len(w)))y = torch.matmul(X,w) + by += torch.normal(0,0.01,y.shape)return X, y.reshape((-1,1))true_w = torch.tensor([2,-3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
print('features:',features[0],'\nlabel:',labels[0])d2l.set_figsize()
d2l.plt.scatter(features[:,(1)].detach().numpy(),labels.detach().numpy(),1)   # 批量数据迭代器
def data_iter(batch_size,features,labels):num_examples = len(features)  # 样本个数indices = list(range(num_examples)) # 样本索引# 这些样本是随即读取的，没有特定的顺序random.shuffle(indices) # 把索引随即打乱for i in range(0, num_examples, batch_size):batch_indices = torch.tensor(indices[i:min(i+batch_size,num_examples)]) # 当i+batch_size超出时，取num_examples         yield features[batch_indices], labels[batch_indices] # 获得随即顺序的特征，及对应的标签batch_size = 10
for X,y in data_iter(batch_size, features, labels):print(X, '\n', y) # 取一个批次后，就break跳出了break# 定义初始化模型参数
w = torch.normal(0,0.01,size=(2,1),requires_grad=True)
b = torch.zeros(1,requires_grad=True)# 定义线性模型
def linreg(X,w,b):"""线性回归模型"""# matmul()表示矩阵乘法，计算结果是每个样本的线性组合return torch.matmul(X,w)+b# 定义损失函数
def squared_loss(y_hat,y):"""均方损失"""return (y_hat - y.reshape(y_hat.shape))**2/2 # 将y统一成与y_hat一样同尺寸   # 定义优化算法，手写SGD更新
# params是待优化的参数列表，例如 [w, b]。
def sgd(params,lr,batch_size):"""小批量随即梯度下降"""with torch.no_grad(): # 不要产生梯度计算，减少内存消耗for param in params: # 每个参数进行遍历param -= lr * param.grad / batch_size # 每个参数进行更新，损失函数没有求均值，所以这里除以 batch_size 求了均值。由于乘法的线性关系，这里除以放在loss的除以是等价的。                          param.grad.zero_() # 每个参数的梯度清零# 训练过程
lr = 0.03
num_epochs = 3
net = linreg # 这里用线性模型，这样写是很方便net赋予其他模型，只需要改一处，不需要下面所有网络模型名称都改
loss = squared_loss# 训练过程
for epoch in range(num_epochs):for X,y in data_iter(batch_size,features,labels):l = loss(net(X,w,b),y) # x和y的小批量损失# 因为l是形状是(batch_size,1)，而不是一个标量。l中所有元素被加到一起# 并以此计算关于[w,b]的梯度l.sum().backward()sgd([w,b],lr,batch_size) #使用参数的梯度更新参数with torch.no_grad():train_l = loss(net(features,w,b),labels)print(f'epoch{epoch+1},loss{float(train_l.mean()):f}')   # 比较真实参数和通过训练学到的参数来评估训练的成功程度
print(f'w的估计误差：{true_w-w.reshape(true_w.shape)}')
print(f'b的估计误差：{true_b-b}')

线性回归的简单实现

这里使用 Pytorch 已有的常用组件

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l
from torch import nn    true_w = torch.tensor([2,-3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w,true_b,1000) # 库函数生成人工数据集    # 调用框架现有的API来读取数据
def load_array(data_arrays,batch_size,is_train=True):"""构造一个Pytorch数据迭代器"""dataset = data.TensorDataset(*data_arrays) # dataset相当于Pytorch的Dataset。一个星号*，表示对list解开入参。      return data.DataLoader(dataset,batch_size,shuffle=is_train) # 返回的是从dataset中随机挑选出batch_size个样本出来     batch_size = 10
data_iter = load_array((features,labels),batch_size) # 返回的数据的迭代器
print(next(iter(data_iter))) # iter(data_iter) 是一个迭代器对象，next是取迭代器里面的元素  # 使用框架的预定义好的层
# nn是神经网络的缩写
# 每个样本有两个特征输出一个值
net = nn.Sequential(nn.Linear(2,1))# 初始化模型参数
net[0].weight.data.normal_(0,0.01) # 使用正态分布替换掉weight变量里面的数据值
net[0].bias.data.fill_(0)  # 偏差bias变量里面的值设置为0
print(net[0])# 计算均方误差使用的是MSELoss类，也称为平方L2范数
loss = nn.MSELoss()  #L1是算术差，L2是平方差# 实例化SGD实例
trainer = torch.optim.SGD(net.parameters(),lr=0.03)# 训练过程代码与从零开始时所做的非常相似
num_epochs = 3
for epoch in range(num_epochs):for X, y in data_iter:  # 从DataLoader里面一次一次把所有数据拿出来
#         print("X:",X)
#         print("y:",y)l = loss(net(X),y) # net(X) 为计算出来的线性回归的预测值trainer.zero_grad() # 梯度清零l.backward()trainer.step()  # SGD优化器优化模型l = loss(net(features),labels)print(f'epoch{epoch+1},loss{l:f}')

Q&A

Q：batchsize 是否会影响模型精度结果？

反直觉的是，小 batchsize 可能会提高精度，因为相当于人为引入（放大）了数据中的噪音，提高了神经网络的泛化性。

Q：为什么优化算法不使用二阶导算法（如牛顿法），说不定结果更快更好？

首先二阶导在计算成本上开销特别大，同时数据维数会指数增加，有的还无法求出准确的二阶导。同时还有可能使得优化曲面不如一阶导平坦，最终收敛结果不见得比一阶导好

6. softmax回归

Softmax回归是逻辑回归的一种推广，主要用于多分类问题。它通过对输入的线性组合进行标准化处理，输出一个概率分布，这样每个类别的预测概率都在 0 到 1 之间，且所有类别的预测概率和为 1。

Softmax回归的目标是计算输入属于每个类别的概率。

• 回归
  • 单连续数值的输出
  • 自然区间
  • 跟真实值的区别作为损失（比如 MSE 损失）
• 分类
  • 输出通常为多个离散值
  • 输出的第i个元素表示预测为第i类的置信度

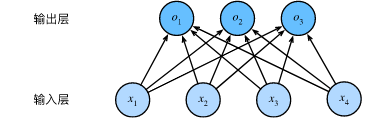
Softmax 回归是以回归之名的分类算法，Softmax 回归也可以看作是拥有多个输出的单层神经网络：

从回归到多类分类——均方损失

从回归到多类分类——无校验比例

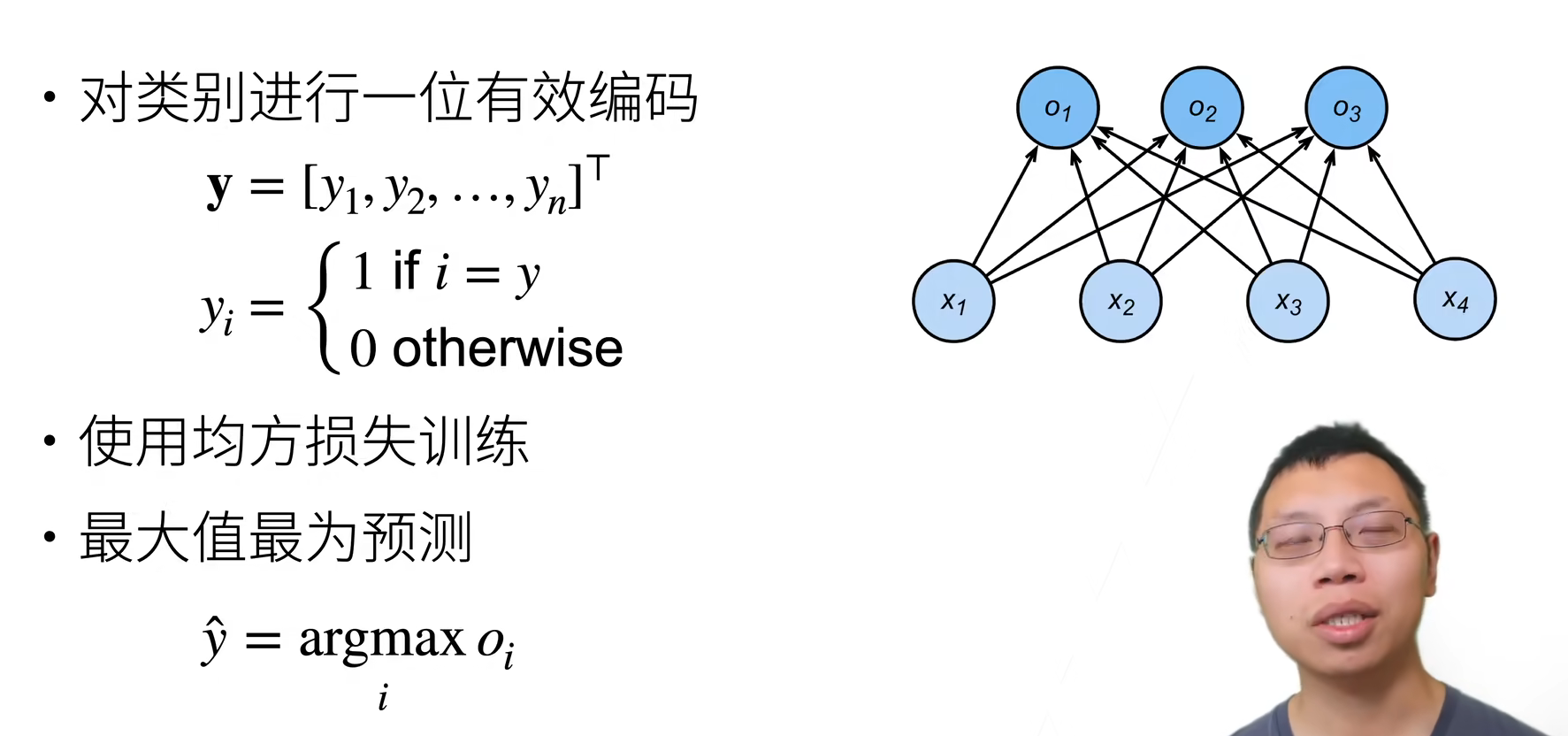
需要更置信的识别正确类（大余量）

正确类的置信度要远大于其他非正确类的置信度，数学表示为一个阈值。

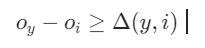
从回归到多类分类——校验比例

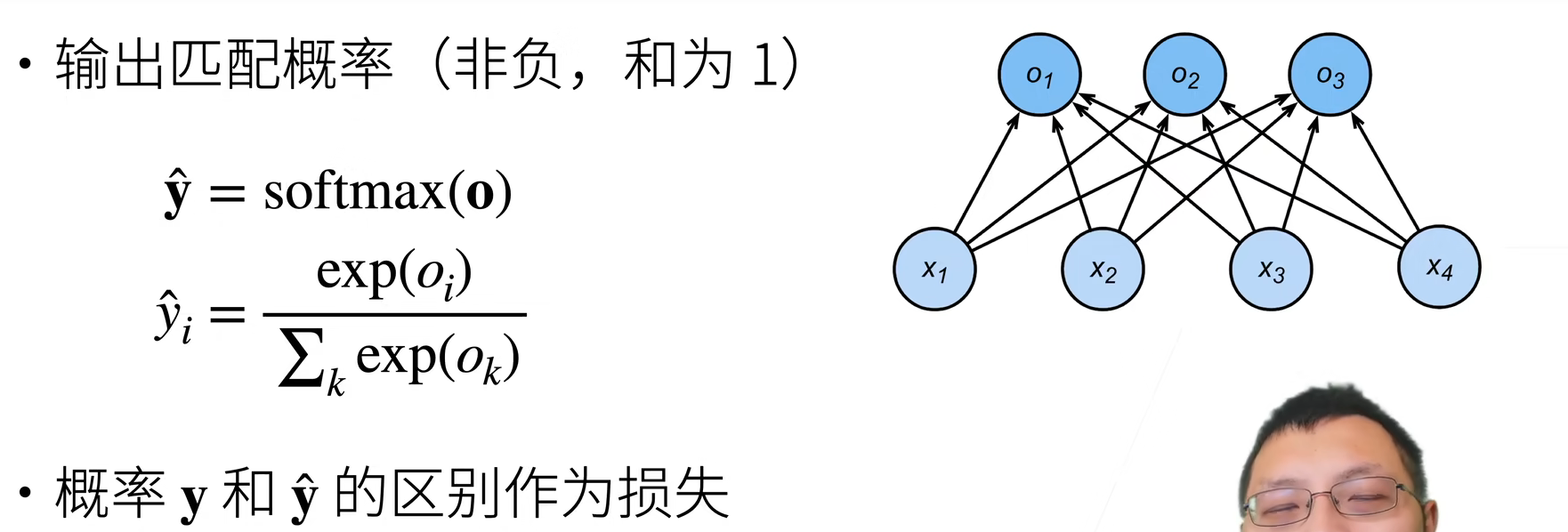
Softmax 和交叉熵损失

损失函数

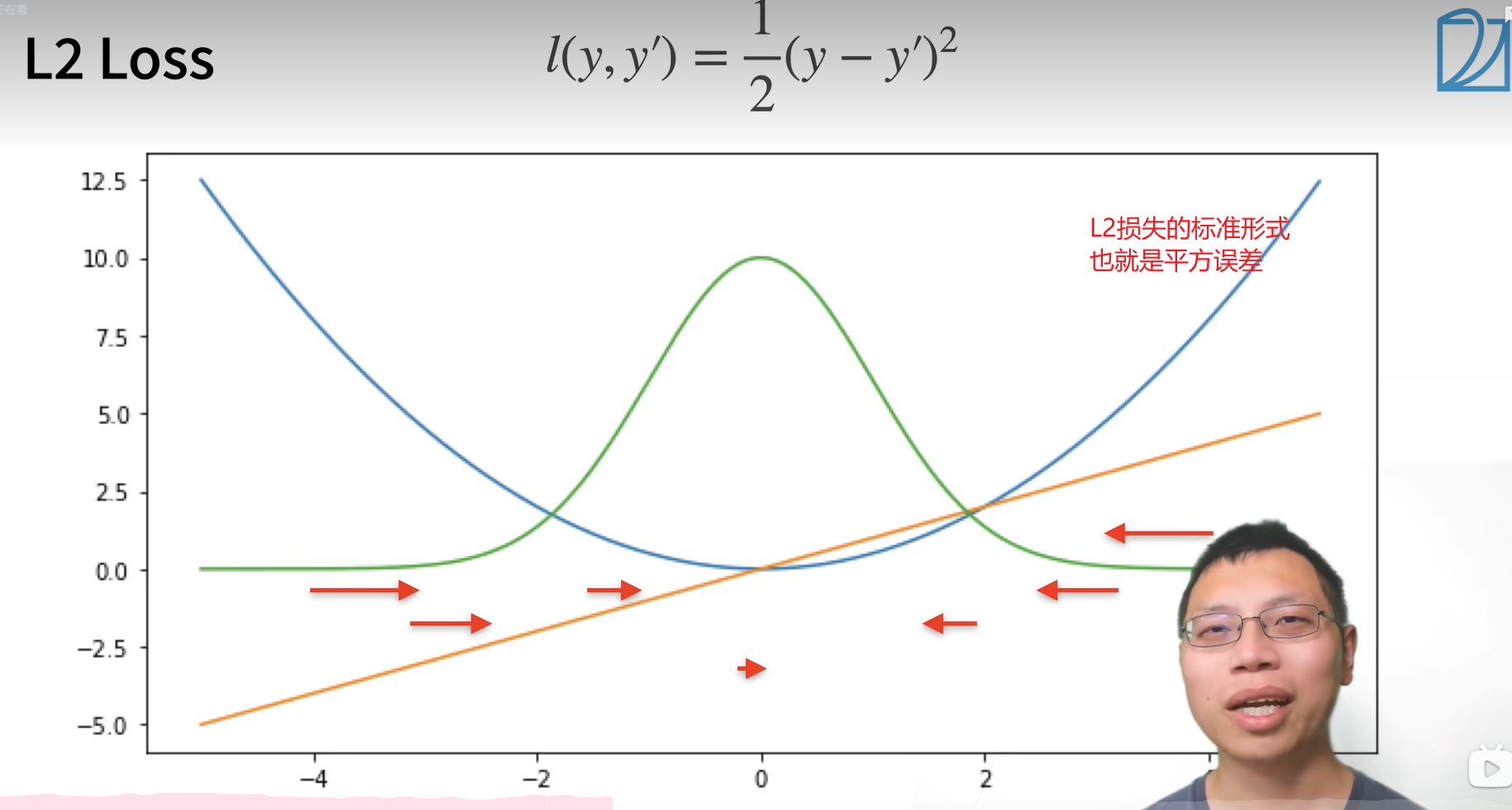
L2 损失函数：

L1 损失函数：

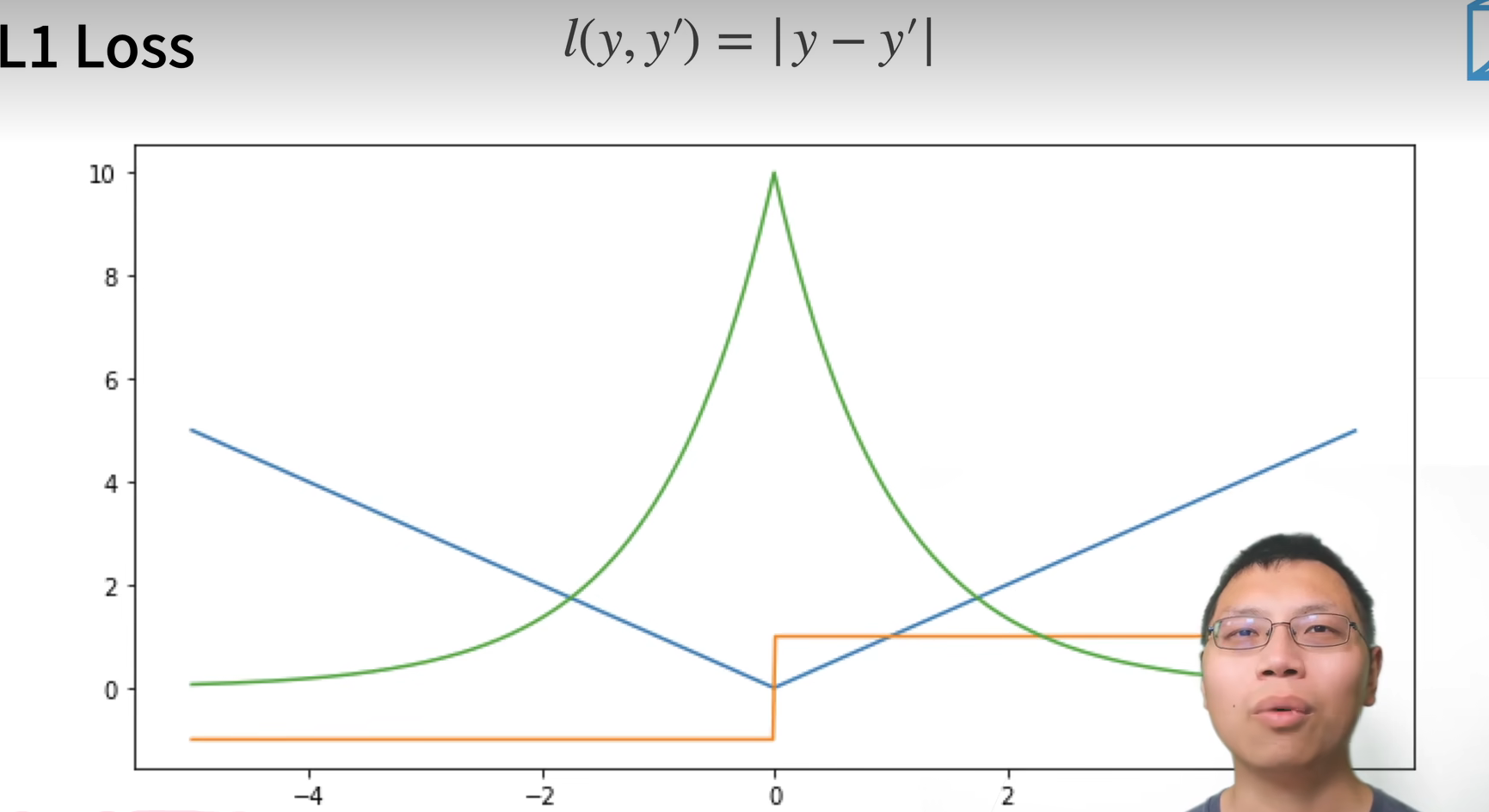
蓝色的线是损失函数的曲线

绿色的线是似然函数

橙色的线是导数，L1大于0，导数是1，L1小于0，导数是-1

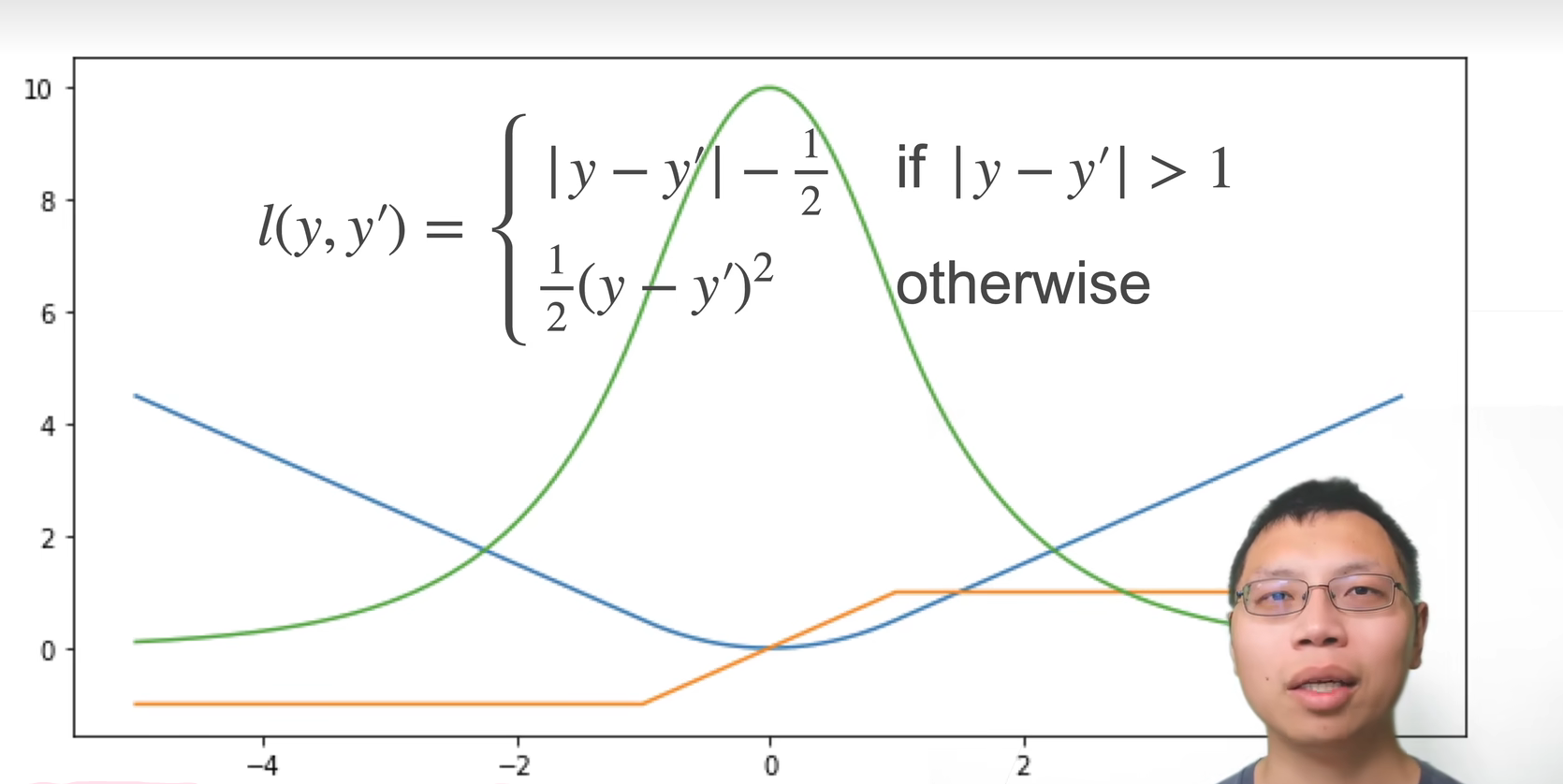
为了互补 L1 损失原点不可导与 L2 损失原点外梯度过大的劣势，提出Huber’s Robust Loss：

图像分类数据集读取

图像分类中使用最为广泛的数据集MNIST，创造与 1986，用于识别手写数字，过于简单，此处用较为复杂的Fashion MNIST。

• 导入各库

%matplotlib inline
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l# SVG是一种无损格式 – 意味着它在压缩时不会丢失任何数据，可以呈现无限数量的颜色。
# SVG最常用于网络上的图形、徽标可供其他高分辨率屏幕上查看。
d2l.use_svg_display() # 使用svg来显示图片，这样清晰度高一些。

• 下载/导入数据

# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式
# 并除以255使得所有像素的数值均在0到1之间
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=True,transform=trans,download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=False,transform=trans,download=True)            
print(len(mnist_train)) # 训练数据集长度
print(len(mnist_test))  # 测试数据集长度print(mnist_train[0][0].shape) # 黑白图片，所以channel通道为1。
print(mnist_train[0][1]) # [0][0]表示第一个样本的图片信息，[0][1]表示该样本对应的标签值输出：
60000
10000
torch.Size([1, 28, 28])
9

• 两个可视化数据集的函数

def get_fashion_mnist_labels(labels):"""返回Fashion-MNIST数据集的文本标签"""text_labels = ['t-shirt','trouser','pullover','dress','coat','sandal','shirt','sneaker','bag','ankle boot']return [text_labels[int(i)] for i in labels]def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):"""Plot a list of images."""figsize = (num_cols * scale, num_rows * scale) # 传进来的图像尺寸，scale 为放缩比例因子_, axes = d2l.plt.subplots(num_rows,num_cols,figsize=figsize)print(_)print(axes) # axes 为构建的两行九列的画布axes = axes.flatten()print(axes) # axes 变成一维数据for i,(ax,img) in enumerate(zip(axes,imgs)):if(i<1):print("i:",i)print("ax,img:",ax,img)if torch.is_tensor(img):# 图片张量ax.imshow(img.numpy())ax.set_title(titles[i])else:# PIL图片ax.imshow(img)
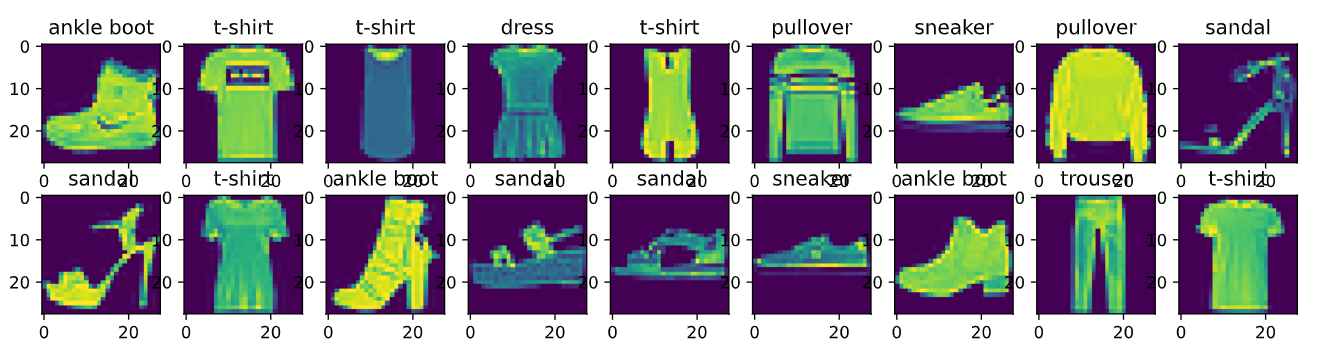
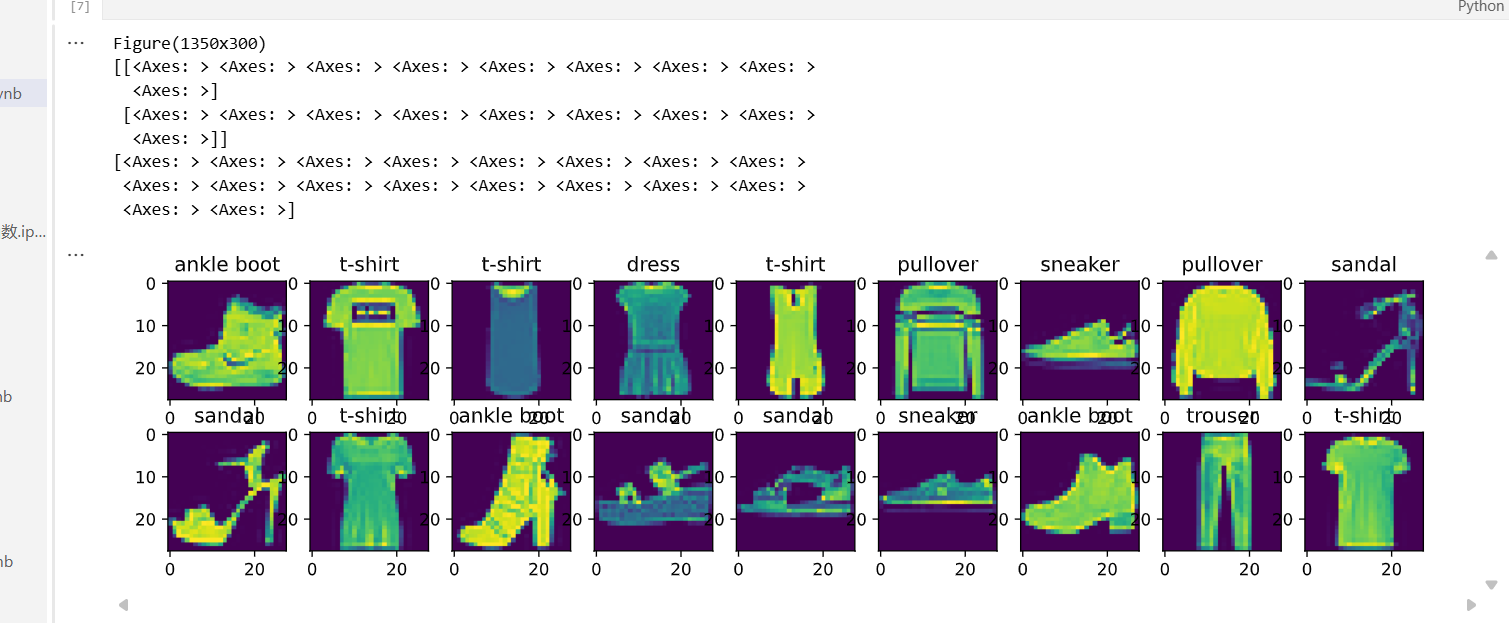
# 几个样本的图像和标签
X, y = next(iter(data.DataLoader(mnist_train,batch_size=18))) # X，y 为仅抽取一次的18个样本的图片、以及对应的标签值
show_images(X.reshape(18,28,28),2,9,titles=get_fashion_mnist_labels(y))

1. X, y = next(iter(data.DataLoader(mnist_train, batch_size=18)))

这行代码做了以下几件事：

data.DataLoader(mnist_train, batch_size=18)：
DataLoader 是 PyTorch 中用于加载数据的工具。mnist_train 是一个 FashionMNIST 数据集对象batch_size=18 表示我们希望每次从数据集中加载 18 张图片（即一个批次）。DataLoader 会自动将数据集 mnist_train 拆分成多个小批次，每个批次包含 18 张图片。

iter()：
将 DataLoader 转换为迭代器。这样我们就可以像访问普通 Python 可迭代对象一样，逐个获取批次的数据。

next()：
获取下一个批次的数据。在这里，它从 DataLoader 中提取出一个包含 18 张图像和它们对应标签的批次数据。
这行代码实际上是获取了一个批次（18张图片及其标签）并将它们分别赋值给变量 X 和 y：

X：是一个张量，包含了 18 张图片。每张图片的尺寸是 28x28，因此 X 的形状为 (18, 28, 28)。

y：是一个张量，包含了每张图片的标签（数字，表示图像的类别）。

2. show_images(X.reshape(18, 28, 28), 2, 9, titles=get_fashion_mnist_labels(y))

这行代码调用了 show_images() 函数来显示这 18 张图片，并且按指定的方式排列（2 行 9 列），并为每张图片添加对应的标签。

X.reshape(18, 28, 28)：
由于 X 是一个张量，其形状可能是 (18, 28, 28) 或 (18, 1, 28, 28)（取决于 DataLoader 如何加载数据）。这里使用 reshape(18, 28, 28) 将 X 的形状调整为 18 张 28x28 像素的图片，以便在图像网格中显示。

2, 9：
这指定了在 show_images() 函数中，显示图片的行数和列数。这里表示：

2 行：即显示 2 行图片

9 列：即显示 9 列图片
这样就能展示 18 张图片（2 x 9 = 18）。

titles=get_fashion_mnist_labels(y)：
get_fashion_mnist_labels(y) 是一个函数，接受一批标签 y（包含 18 个标签），并返回这些标签对应的文本标签（例如 t-shirt, dress 等）。
该函数将返回一个包含 18 个标签名称的列表，并将它作为标题传递给 show_images()。每张图片上都会显示对应的类标签（如 t-shirt、dress 等）。

• 读取一小批量图片

batch_size = 256  #传入批量大小为256
def get_dataloader_workers():"""使用4个进程来读取的数据"""return 4train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True,num_workers=get_dataloader_workers())timer = d2l.Timer() # 计时器对象实例化，开始计时
for X,y in train_iter:  # 遍历一个batch_size数据的时间continue
f'{timer.stop():.2f}sec' # 计时器停止时，停止与开始的时间间隔事件

• 定义数据读取的函数

def load_data_fashion_mnist(batch_size, resize=None):  #@save"""下载Fashion-MNIST数据集，然后将其加载到内存中"""trans = [transforms.ToTensor()]# 指定给一个方法集if resize:trans.insert(0,transforms.Resize(resize)) # 如果有Resize参数传进来，就进行resize操作# 如果制定了大小，则插入一个图片格式改变方法，再转换为张量trans = transforms.Compose(trans)# 打包成torch可理解的函数集。mnist_train = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=True,transform=trans,download=True)mnist_test = torchvision.datasets.FashionMNIST(root="01_data/01_DataSet_FashionMNIST",train=False,transform=trans,download=True)            return (data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers()),data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers()))       

Softmax 回归的从零开始实现

• 引入包

import torch
from IPython import display
from d2l import torch as d2lbatch_size = 256
train_iter, test_iter = load_data_fashion_mnist(batch_size) # 返回训练集、测试集的迭代器     

• 定义权重

num_inputs = 784
#将图片矩阵铺平，变成一个向量，但会损失空间信息 28*28
num_outputs = 10
#数据集有10个类，所以模型输出维度为10
# 高斯随机权重的值，均值为0，方差为0.01
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)
#每个输出都有偏移print(w.shape)  # torch.Size([784, 10])
print(b.shape)   # orch.Size([10])

• 定义 Softmax 函数

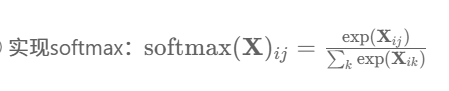
# 给定一个矩阵，可以对所有元素求和
import torch
from IPython import display
from d2l import torch as d2lx = torch.tensor([[1.0,2.0,3.0],[4.0,5.0,6.0]])
print(x)
print(x.sum(0,keepdim=True)) # 按照列求和
print(x.sum(1,keepdim=True)) # 按照行求和输出：
tensor([[1., 2., 3.],[4., 5., 6.]])
tensor([[5., 7., 9.]])
tensor([[ 6.],[15.]])

def softmax(X):#对矩阵的每一行做softmaxX_exp = torch.exp(X) # #按照行内求和partition = X_exp.sum(1,keepdim=True) return X_exp / partition # 这里应用了广播机制# 将每个元素变成一个非负数。此外，依据概率原理，每行总和为1。
X = torch.normal(0,1,(2,5))  # 两行五列的数，数符合标准正态分布
print(X)
X_prob = softmax(X)
print(X_prob) # 形状没有发生变化，还是一个两行五列的矩阵，Softmax转换后所有值为正的  
print(X_prob.sum(1)) # 相当于 X_prob.sum(axis=1) 按行求和，概率和为1输出：
tensor([[ 1.3342, -0.3354,  1.5634, -0.2688, -0.1783],[ 1.8692, -0.4317,  0.0436, -0.5774,  1.6731]])
tensor([[0.3487, 0.0657, 0.4386, 0.0702, 0.0768],[0.4609, 0.0462, 0.0743, 0.0399, 0.3788]])
tensor([1., 1.])

• 定义模型

def net(X):# -1为默认的批量大小，表示有多少个图片，每个图片用一维的784列个元素表示 return softmax(torch.matmul(X.reshape((-1,w.shape[0])),w)+b)     # matmul()是矩阵乘法# reshape(-1, n)中，“-1”表示在第二维为n条件下，自动推导第一维数值# 此处将batch_size=256张图组成的四维张量（256x1x28x28），重整为二维矩阵（256x764）。# shape()返回维度的列表

模型以类别预测的概率进行 softmax 计算后作为输出。

• 代码技巧，根据标号索引

# 交叉熵损失
# 创建一个数据y_hat，其中包含2个样本在3个类别的预测概率，使用y作为y_hat中概率的索引。
#以y的元素数值按顺序作为y_hat的对应数组元素的索引，y = torch.tensor([0,2]) # 标号索引
y_hat = torch.tensor([[0.1,0.3,0.6],[0.3,0.2,0.5]]) # 两个样本在3个类别的预测概率   
y_hat[[0,1],y] # 把第0个样本对应标号"0"的预测值拿出来、第1个样本对应标号"2"的预测值拿出来输出：
tensor([0.1000, 0.5000])

• 交叉熵损失

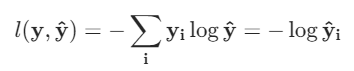
# 交叉熵损失函数
# y_hat 是模型的输出，y 是真实标签
def cross_entropy(y_hat, y):print(list(range(len(y_hat))))return -torch.log(y_hat[range(len(y_hat)),y]) # y_hat[range(len(y_hat)),y]为把y的标号列表对应的值拿出来。传入的y要是最大概率的标号      print(y_hat.shape)
print(y.shape)
cross_entropy(y_hat,y)输出：
torch.Size([2, 3])
torch.Size([2])
[0, 1]
tensor([2.3026, 0.6931])

• 统计分类正确的样本数量

# 将预测类别与真实y元素进行比较
def accuracy(y_hat,y):"""计算预测正确的数量"""if len(y_hat.shape) > 1 and y_hat.shape[1] > 1: # y_hat.shape[1]>1表示不止一个类别，每个类别有各自的概率   y_hat = y_hat.argmax(axis=1) # y_hat.argmax(axis=1)为求行最大值的索引print("y_hat:",y_hat)cmp = y_hat.type(y.dtype) == y # 先判断逻辑运算符==，再赋值给cmp，cmp为布尔类型的数据print("cmp:",cmp)return float(cmp.type(y.dtype).sum()) # 获得y.dtype的类型作为传入参数，将cmp的类型转为y的类型（int型），然后再求和       print("accuracy(y_hat,y) / len(y):",accuracy(y_hat,y) / len(y))
print("accuracy(y_hat,y):",accuracy(y_hat,y))
print("len(y):",len(y))输出：
y_hat: tensor([2, 2])
cmp: tensor([False,  True])
accuracy(y_hat,y) / len(y): 0.5
y_hat: tensor([2, 2])
cmp: tensor([False,  True])
accuracy(y_hat,y): 1.0
len(y): 2

• 计算模型在指定数据集上的精度

# 可以评估在任意模型net的准确率
def evaluate_accuracy(net,data_iter):"""计算在指定数据集上模型的精度"""# 如果net模型是torch.nn.Module实现的神经网络的话，将它变成评估模式 if isinstance(net,torch.nn.Module):     net.eval()  # 将模型设置为评估模式metric = Accumulator(2) # 正确预测数、预测总数，metric为累加器的实例化对象，里面存了两个数for X, y in data_iter:# net(X)将X输入模型，获得预测值。y.numel()为样本总数metric.add(accuracy(net(X),y),y.numel())return metric[0] / metric[1] # 分类正确的样本数 / 总样本数

# Accumulator实例中创建了2个变量，用于分别存储正确预测的数量和预测的总数量
class Accumulator:"""在n个变量上累加"""def __init__(self,n):self.data = [0,0] * ndef add(self, *args):self.data = [a+float(b) for a,b in zip(self.data,args)] # zip函数把两个列表第一个位置元素打包、第二个位置元素打包....def reset(self):self.data = [0.0] * len(self.data)def __getitem__(self,idx):return self.data[idx]# 再来回溯metric = Accumulator(2), self.data = [0.,0.]
# metric.add(accuracy(net(X), y), y.numel())
# y.numel()=10类，accuracy(net(X), y)=预估正确数
# zip([0.,0.], *args= metric.add(accuracy(net(X), y), y.numel())
# *args会把传入的单个参数打包成元组，假设预测对8个，即 args=(8,10)
# 转化为float方便于计算
# return metric[0] / metric[1]evaluate_accuracy(net, test_iter)  #0.06301666666666667

以上完成了测试数据集迭代一个 batch 的初始精确度，因为总共是 10 类，网络参数是随机化，所以精度是 10%左右。

• Softmax 训练函数

def train_epoch_ch3(net, train_iter, loss, updater):#判断函数是手动还是模块调用，提高函数适用性。if isinstance(net, torch.nn.Module):net.train()##train()函数与eval()函数相对应，可以理解为此处启用求导。metric = Accumulator(3)for X, y in train_iter:# train_iter可以看作一个迭代器，每次取batch_size=256的数据集训练一组，然后再换下一组训练，直至60000个数据都训练结束。y_hat = net(X)l = loss(y_hat, y)#torch.optim.Optimizer是torch优化器的包if isinstance(updater, torch.optim.Optimizer):#updater归零梯度。updater.zero_grad()#自带的loss已求了平均l.backward()#Optimizer更新参数updater.step()metric.add(float(l) * len(y), accuracy(y_hat, y),y.size().numel())# 因为一个batch求出的损失l是平均损失，乘len(y)代表恢复成一个batch的总损失else:l.sum().backward()## X是二维向量（256x764），此处updater需要传入批量大小参数，即第0维updater(X.shape[0])metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())return metric[0] / metric[2], metric[1] / metric[2]

• 动画显示

class Animator:def __init__(self, xlabel=None, ylabel=None, legend=None,xlim=None, ylim=None, xscale= 'linear', yscale='linear',fmts=('-','m--', 'g-', 'r:'), nrows=1, ncols=1,figsize=(3.5, 2.5)):# x/ylabel:x/y轴标签#legend:图例#x/ylim(x/ymin, x/ymax):x/y轴的上下极限。#x/yscale：x/y轴缩放比例#'-':实线,'m--'：品红色虚线, 'g-'：绿色实线, 'r:'：红色点线。#nrows/ncols：指定多子图行列数量。if legend is None:legend = []d2l.use_svg_display()#用svg格式显示图片。self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize= figsize)if nrows * ncols == 1:self.axes = [self.axes,]#一张图就是[0]，保证axes是一个数列。self.config_axes = lambda: d2l.set_axes(self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)#可以视为lambda self:#可以理解为定义图像self.X, self.Y, self.fmts = None, None, fmtsdef add(self, x, y):# 向图表中添加多个数据点if not hasattr(y, "__len__"):#hasattr(arg)函数表示是否有属性arg#也就是说int没有长度，需要创造列表。y = [y]n = len(y)if not hasattr(x, "__len__"):x = [x] * n# x和y一样长if not self.X:#判断self.X是否为空self.X = [[] for _ in range(n)]# _表示在循环此处并不想创建变量#创建那个空数组，组成一个n*1的二维空矩阵if not self.Y:self.Y = [[] for _ in range(n)]for i, (a, b) in enumerate(zip(x, y)):if a is not None and b is not None:self.X[i].append(a)self.Y[i].append(b)#将a,b的值分别加入空数组中，组成n*1实值矩阵self.axes[0].cla()#cla()清除图像中的曲线for x, y, fmt in zip(self.X, self.Y, self.fmts):self.axes[0].plot(x, y, fmt)self.config_axes()display.display(self.fig)display.clear_output(wait=True)

10. 定义训练函数

   def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],legend=['train loss', 'train acc', 'test acc'])#显示图像for epoch in range(num_epochs):train_metrics = train_epoch_ch3(net, train_iter, loss, updater)#对数据集训练，return metric[0] / metric[2], metric[1] / metric[2]两个比例。#函数return的多个值是一个元组return a, b = (a, b)test_acc = evaluate_accuracy(net, test_iter)#数据集的正确率统计animator.add(epoch + 1, train_metrics + (test_acc,))#显示图像train_loss, train_acc = train_metrics

11. 调用 sgd 优化方法

lr = 0.1
#设置学习率。
def updater(batch_size):return d2l.sgd([W, b], lr, batch_size)
##定义优化函数，直接调用sgd（在线性回归中定义过的），对w和b求梯度变化，然后清零梯度，再通过step()更新样本，相当于循环。

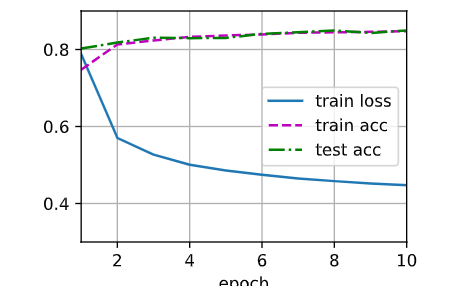
12. 开始训练

num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

13. 用测试集预测

def predict_ch3(net, test_iter, n=10):  #@save"""预测标签（定义见第3章）"""for X, y in test_iter:break#只从遍历出一个批量trues = d2l.get_fashion_mnist_labels(y)preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))titles = [true +'\n' + pred for true, pred in zip(trues, preds)]d2l.show_images(X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])#挑出前n个数据作图，行1列n。predict_ch3(net, test_iter)

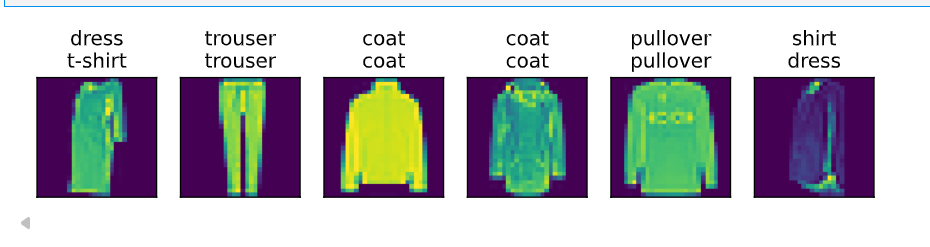
Softmax 的简易实现

import torch
from torch import nn
from d2l import torch as d2lbatch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)# 定义网络
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))
# Sequential()函数打包模块序列，使运算按顺序进行，即Flatten的output是Linear的input。
# Flatten()函数把任意维度tensor第0维保留，后续维“拉平”展开为第1维
# Linear()函数,input=784是输入的features，output=10是输出
# Linear()函数,自带weight和bias（default=True）属性，如果没有指定，系统会用内置算法提供初始权重和偏差。
# Linear()函数对输入特征进行y=Wx+b的线性变换。
def init_weights(m):if type(m) == nn.Linear:nn.init.normal_(m.weight, std=0.01)# 初始化权重层# torch.nn.init.normal_(tensor, mean=0.0, std=1.0)# fills the input Tensor with values drawn from the normal distribution
# apply(fn)函数的参数是一个函数，对net里的每一层都进行fn函数的操作。
net.apply(init_weights)# l = loss(y_hat, y)
# CrossEntropyLoss()函数计算input(y_hat)与target(y)的交叉熵损失。
# CrossEntropyLoss()函数自带Softmax运算。
# CrossEntropyLoss()函数的默认reduction=mean，表示对所有损失之和求平均。
loss = nn.CrossEntropyLoss()
num_epochs = 10
learning_rate = 0.1  # 直接定义学习率# 使用正确的参数调用 train_ch6
# 参数顺序: net, train_iter, test_iter, num_epochs, lr, device
# net.parameters()方法返回模块参数的迭代器。
# torch.optim.SGD()对传入参数进行SGD运算
# SGD的step()方法，进行一次sgd算法
# SGD的zero_grad()方法，随所有训练梯度清零。
#对应前方的updater
#        if isinstance(updater, torch.optim.Optimizer):
#            updater.zero_grad() 先清零
#            l.backward()        再求导
#            updater.step()      一次参数优化
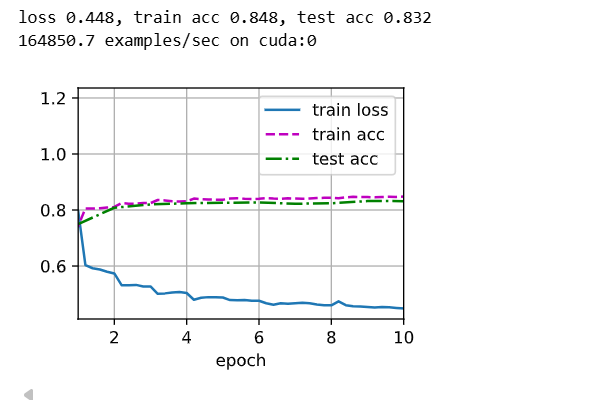
d2l.train_ch6(net, train_iter, test_iter, num_epochs, learning_rate, d2l.try_gpu())

Q&A

Q：softmax 解决的多分类问题，会不会出现类别不平衡？

如果要用机器学习解决多分类问题，那么训练数据就要尽量保证各类都有充足的样本，且数量最好能接近均衡，这样学习算法才能更全面的提取各类的特征，如果某类训练数据过少，则模型对该类的预测也会不可靠。

7.感知机（Perceptron）

感知机可以看作是一个简单的线性分类器，它试图通过一条决策边界（在二维空间中是一条直线，在高维空间中是一个超平面）将数据分为两类。其核心思想是通过输入数据的加权和，使用激活函数（通常是阶跃函数）来做出分类决策。

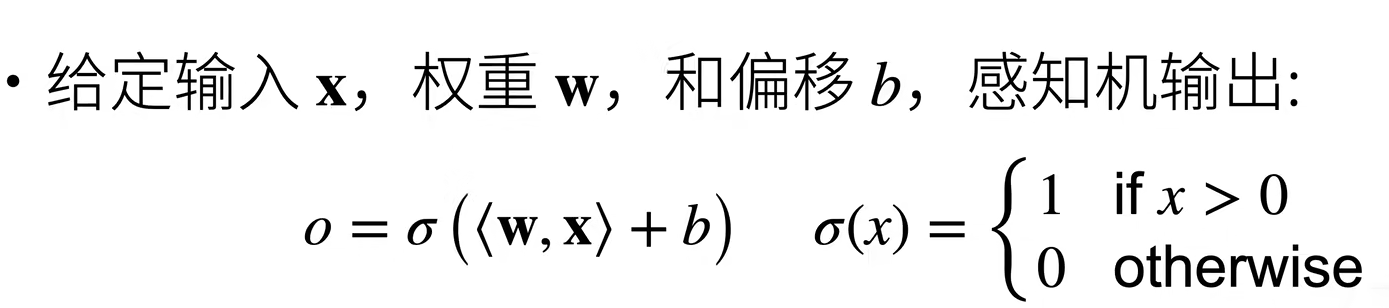
感知机工作步骤：

• 初始化权重和偏置：首先，感知机的权重和偏置通常是随机初始化的。

• 输入数据：将输入数据传入感知机模型。

• 计算加权和：通过每个输入特征与其对应的权重相乘，然后加上偏置，计算加权和 zzz。

• 激活输出：通过阶跃函数计算输出值（0 或 1）。

• 更新权重：根据预测结果和真实标签之间的差距，调整权重和偏置。这个过程使用 梯度下降法（或其它优化算法）进行。

• 二分类：感知机输出离散的两类

  • VS 线性回归：输出实数；
  • VS Softmax 回归：输出概率；

• 如何训练感知机

initialize w=0 and b=0
repeatif y_i[<w,x_i>+b] <= 0 then:w <- w + y_i·x_i and b <- b + y_iend if
until all classified correctly

等价于使用批量大小为 1 的梯度下降，并使用如下的损失函数

把每一个样本单独带入更新梯度。

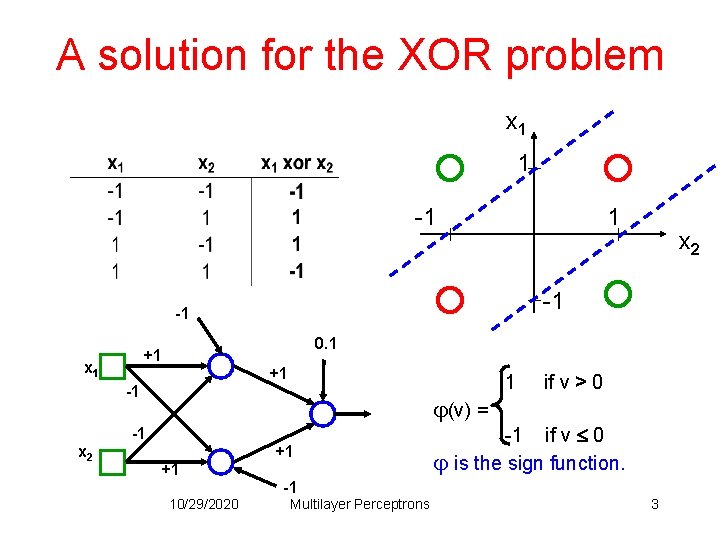
• XOR 问题(Minsky&Papert,1969)

计算机科学家Marvin Minsky（后世人们称他为：人工智能之父）和 Seymour Papert 在其 1969 年的书《感知器》（Perceptrons）中提供了单层人工网络无法执行 XOR 的证据。

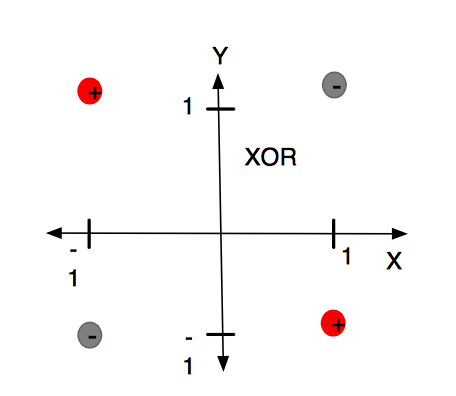
感知机不能拟合XOR函数，它只能产生线性分割面。因为感知机的分割面是线性的，在上图中不管怎么做，都无法画出一条线可以完美分类红灰两种类别。这个结论是如此令人震惊，以至于许多计算机科学家将其归咎于神经网络研究在 1980 年代前的持续低迷状态，因此造成了第一次 AI 寒冬。

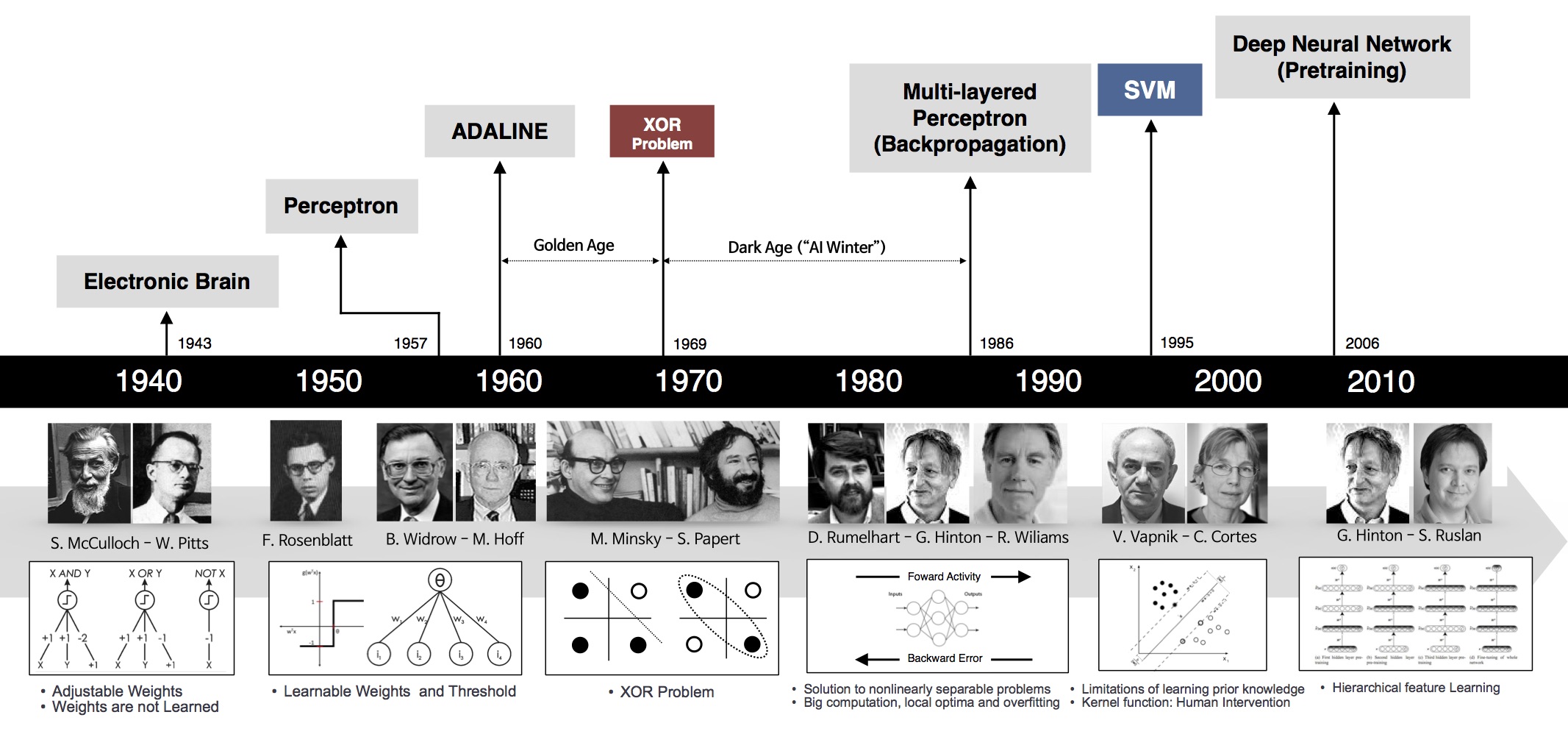
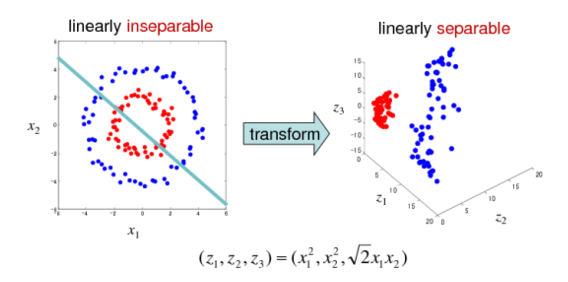
后来引入非线性激活函数（如“核方法”、“支持向量机（SVM）”等）、多层感知机后，对特征空间进行非线性扭曲变换，才使 XOR 之类问题转换为线性可分问题得以解决。

多层感知机(MLP)

既然一层学不了，就用简单函数的组合，层层嵌套，解决问题

单隐藏层——单分类

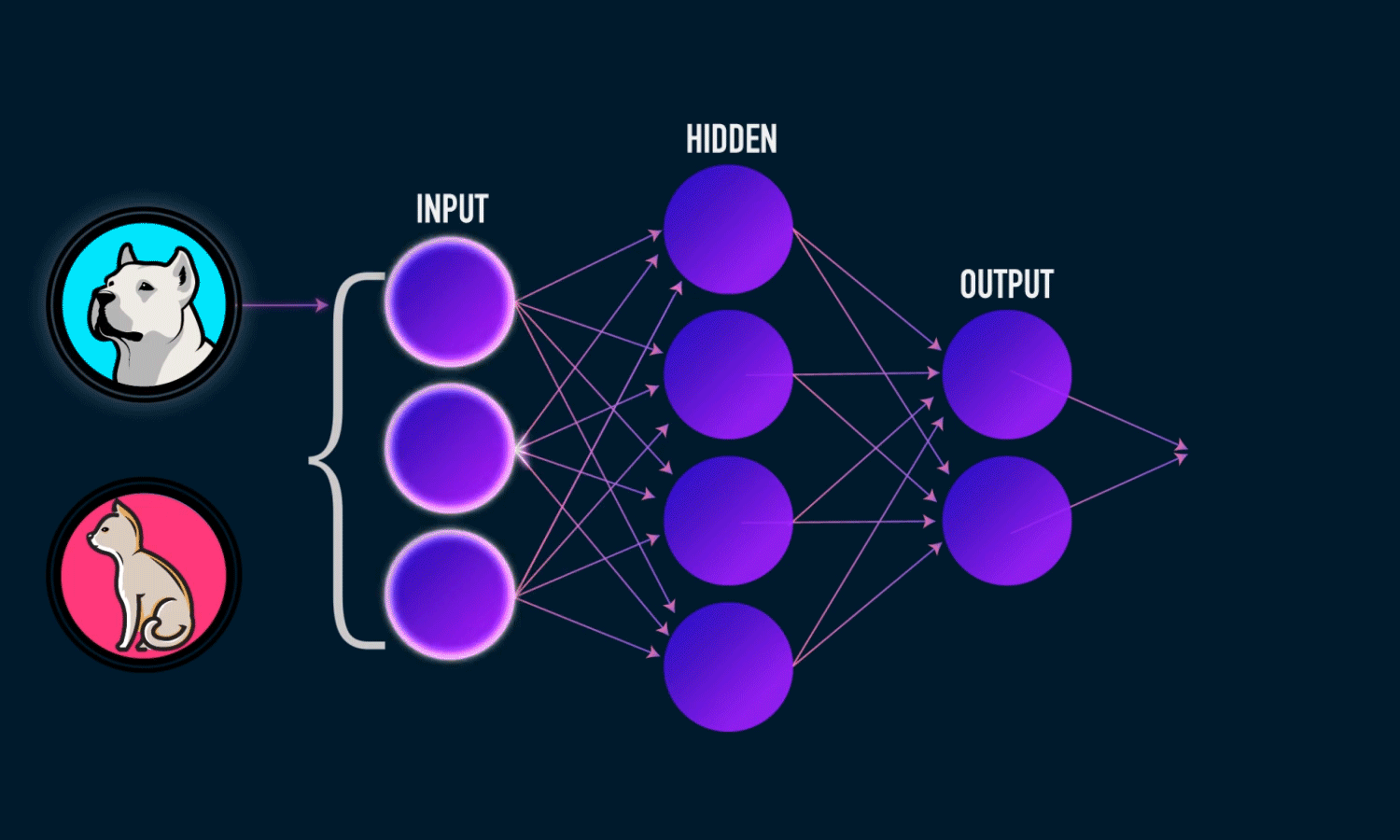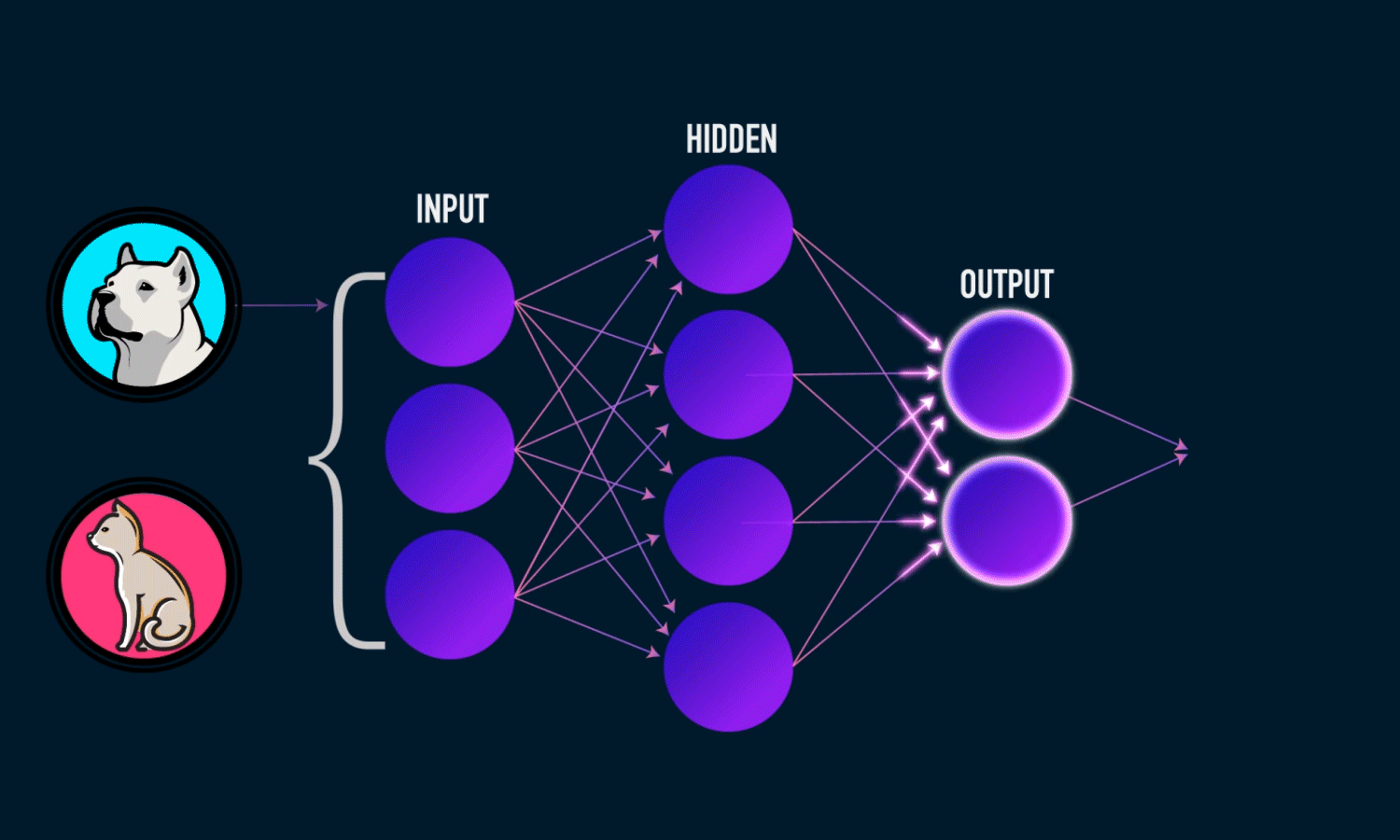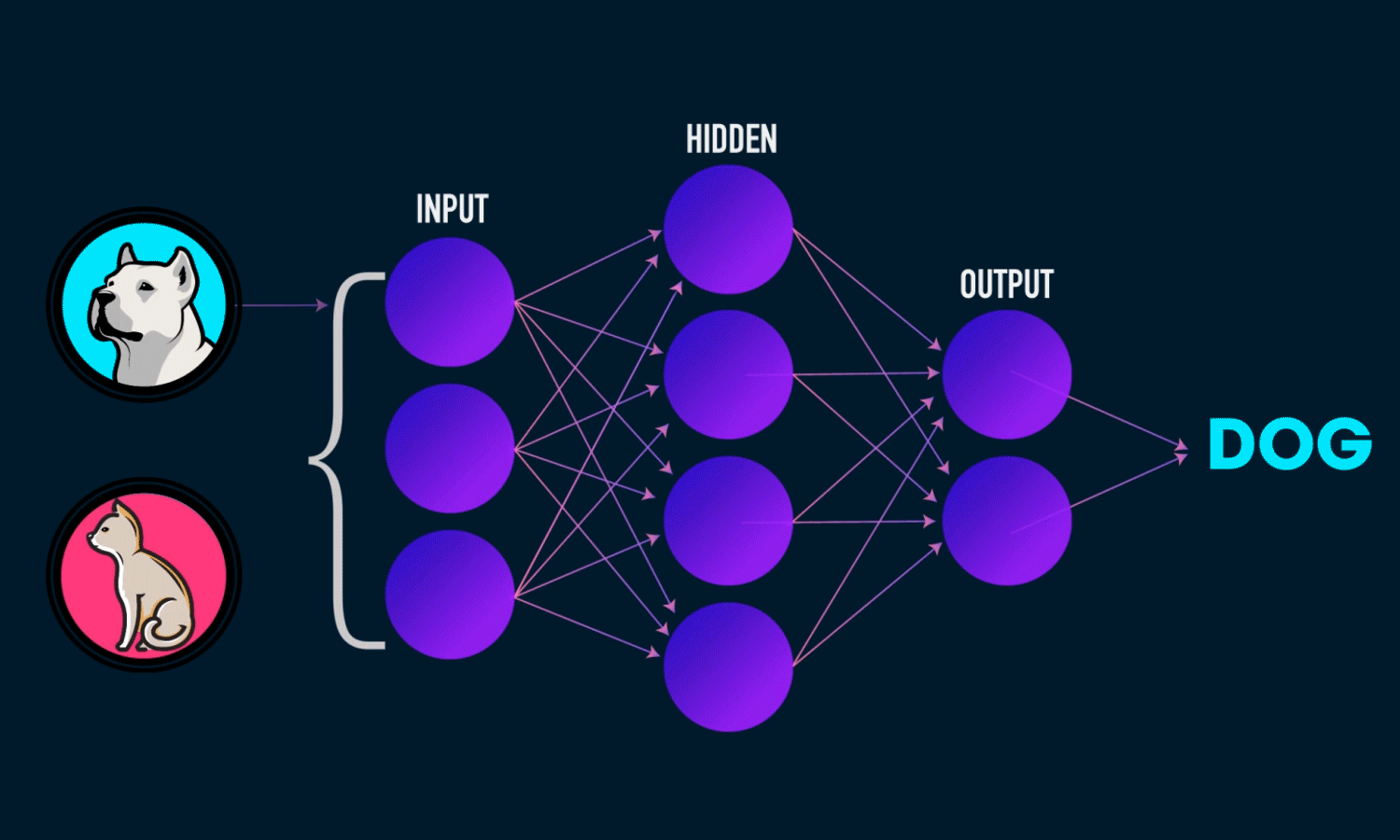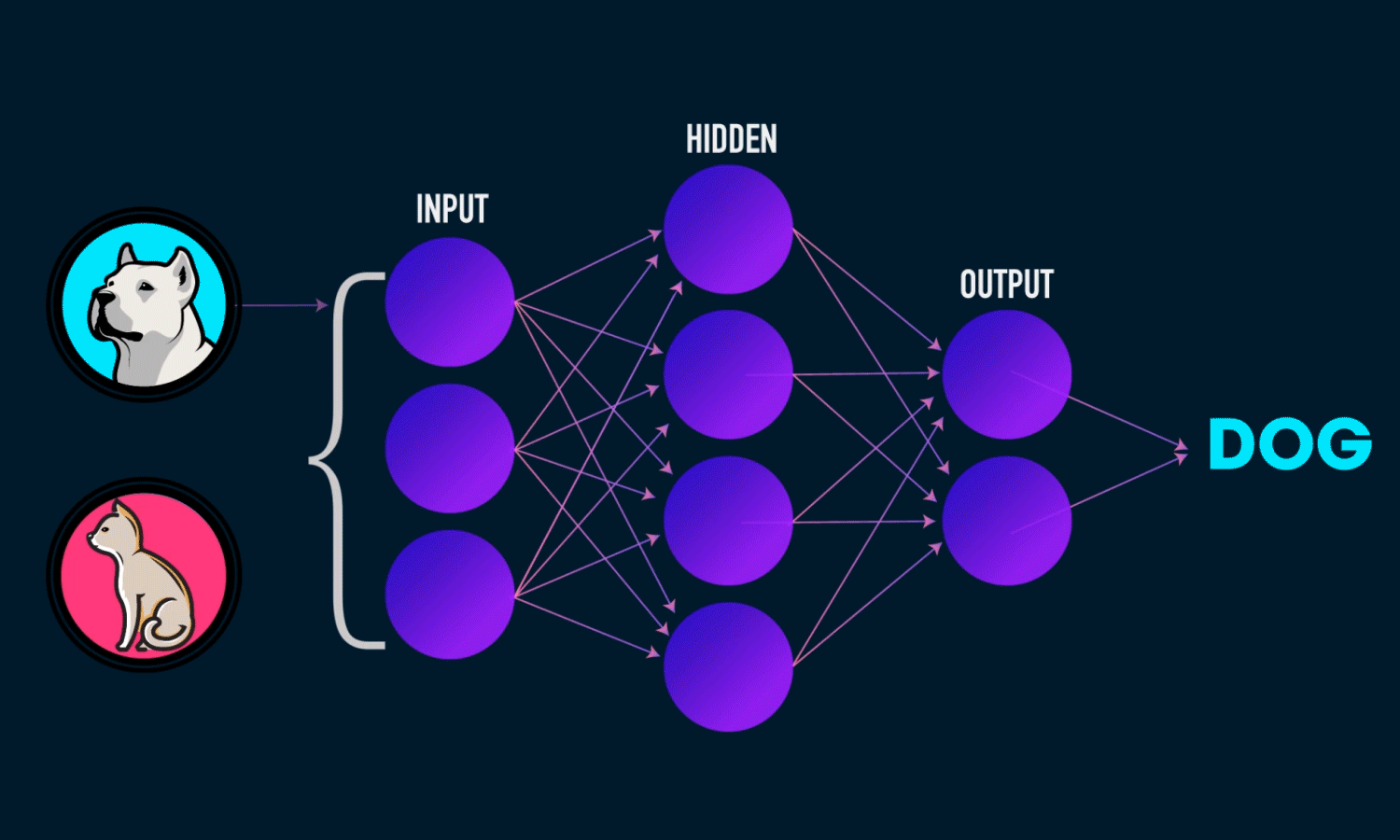
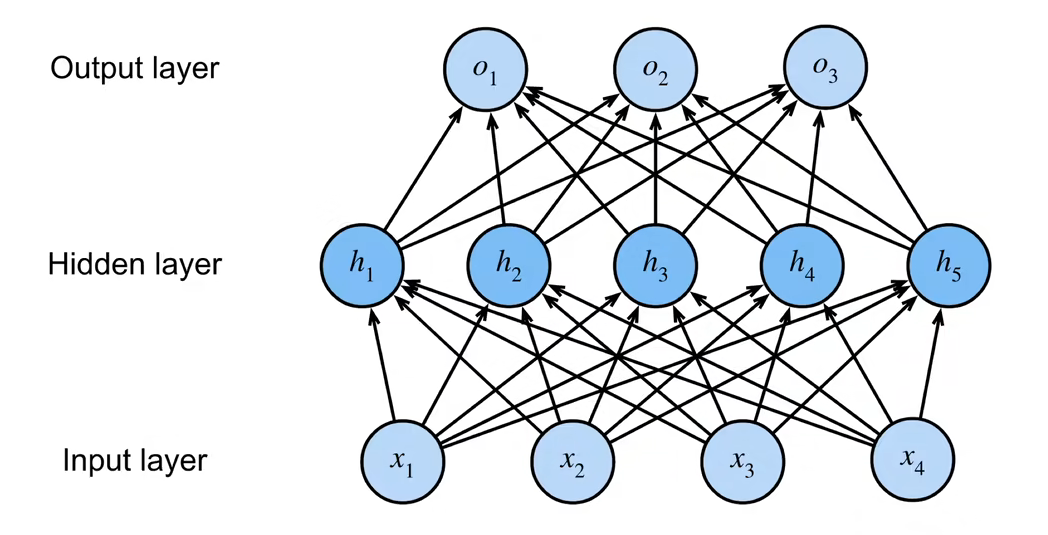
隐藏层的大小是超参数

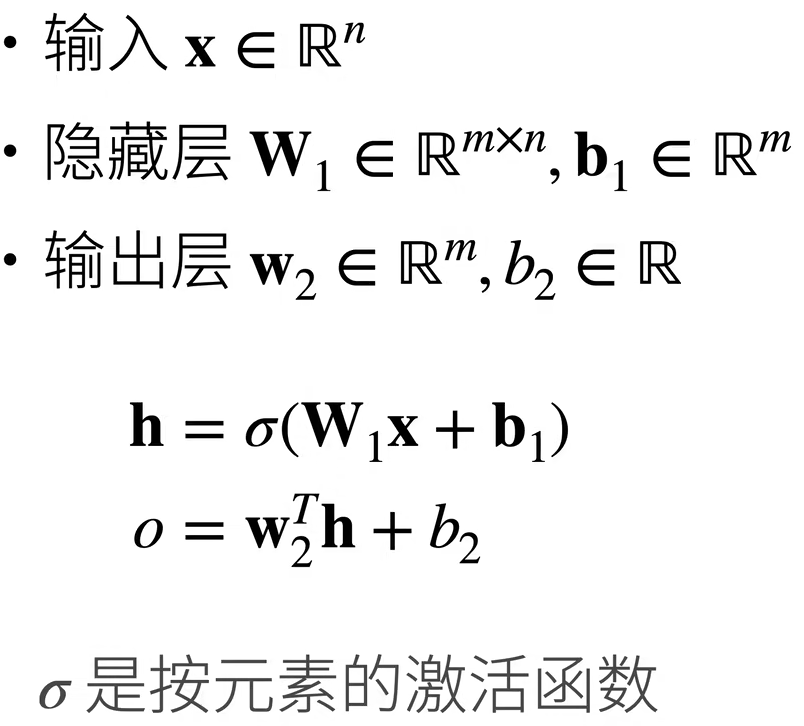
激活函数的引入使得神经网络变得非线性，而非线性使得神经网络能够拟合更加复杂的函数和模式，处理更复杂的数据任务。

• 常用激活函数
  • Sigmoid 函数（多用于二分类问题的 Logistic 回归）

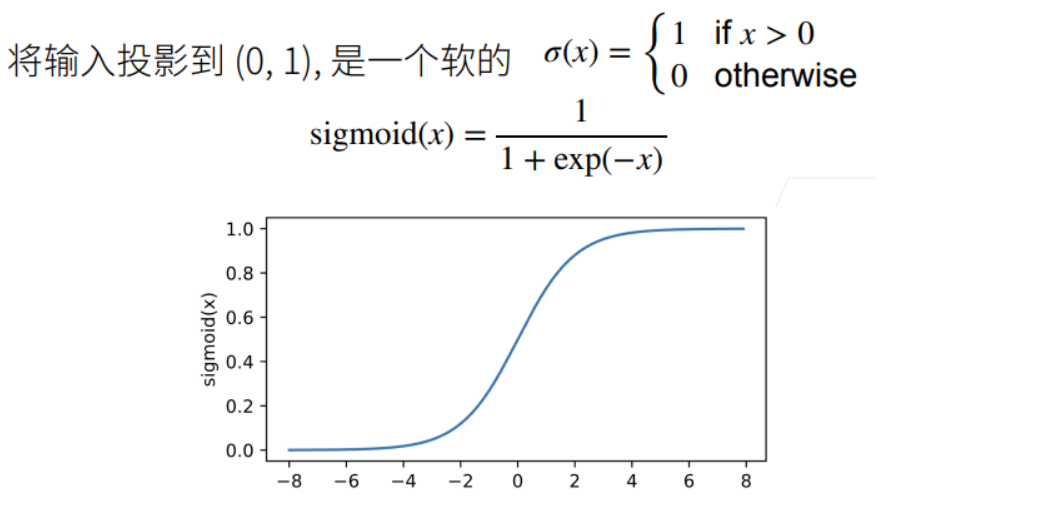
• Tanh 函数

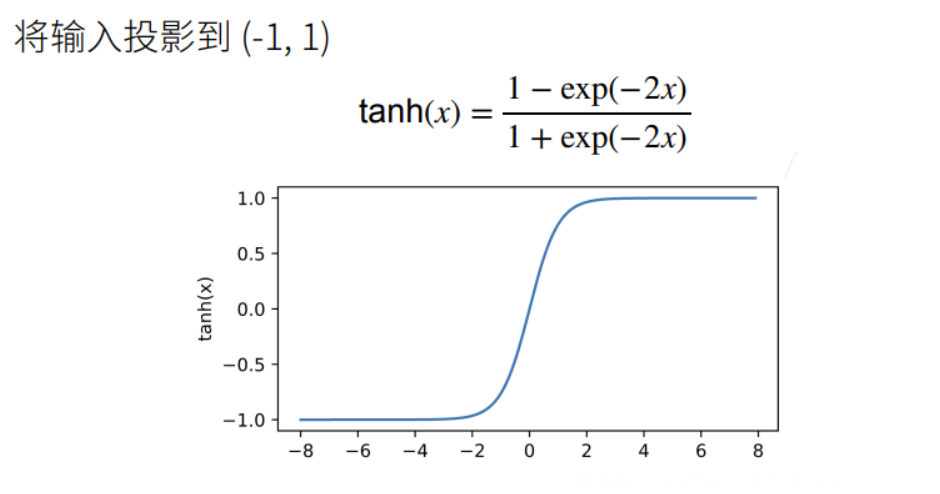
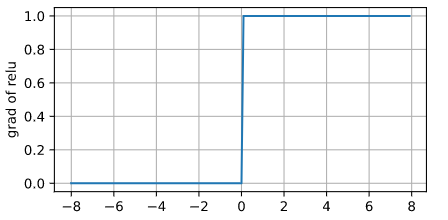
• ReLU 函数(Rectified Linear Unit)

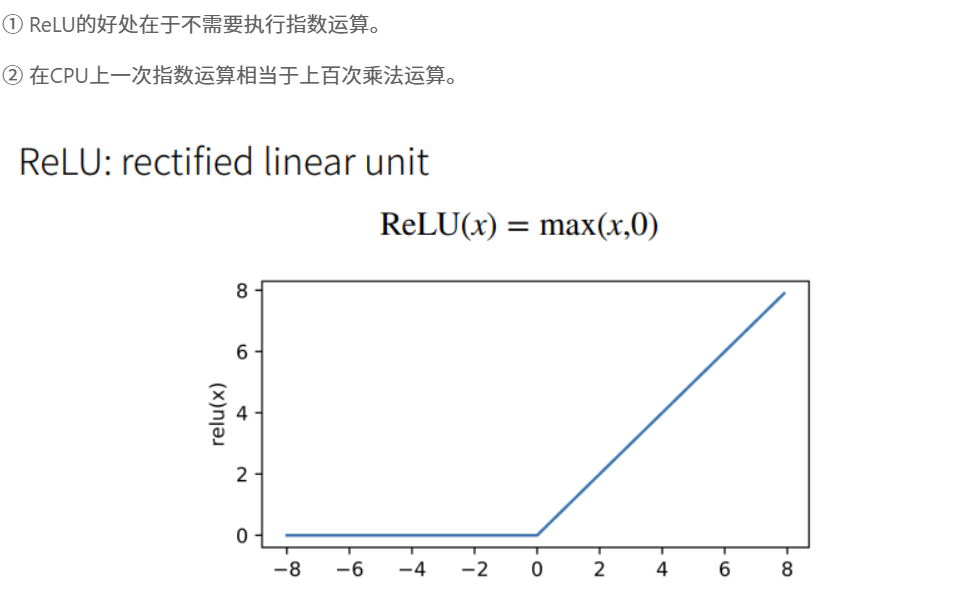
ReLU 激活函数应用广泛的主要原因是计算简便，求导方便，同时没有指数运算（一次指数运算在 CPU 上相当于上百次乘法运算 😮）

多分类感知机——相当于在 Softmax 回归加入一层隐藏层

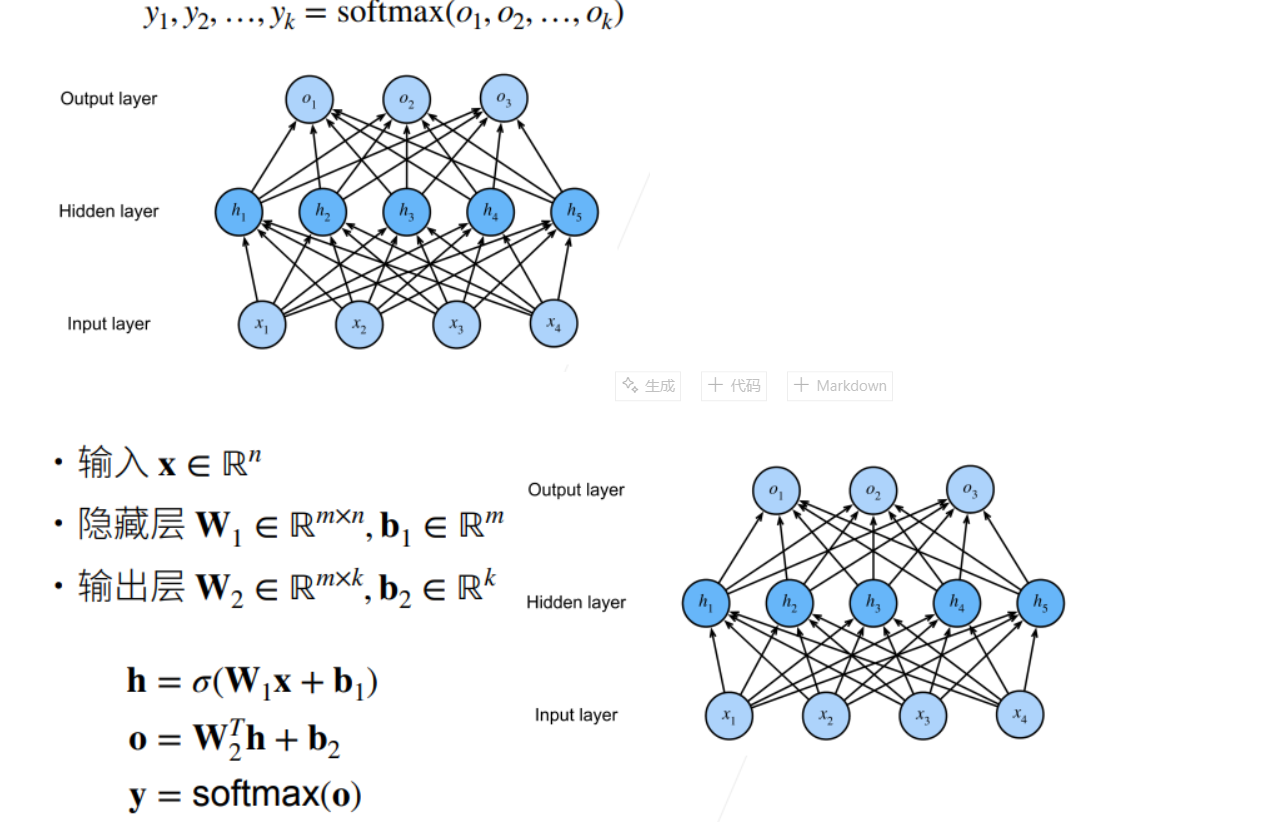
多隐藏层感知机

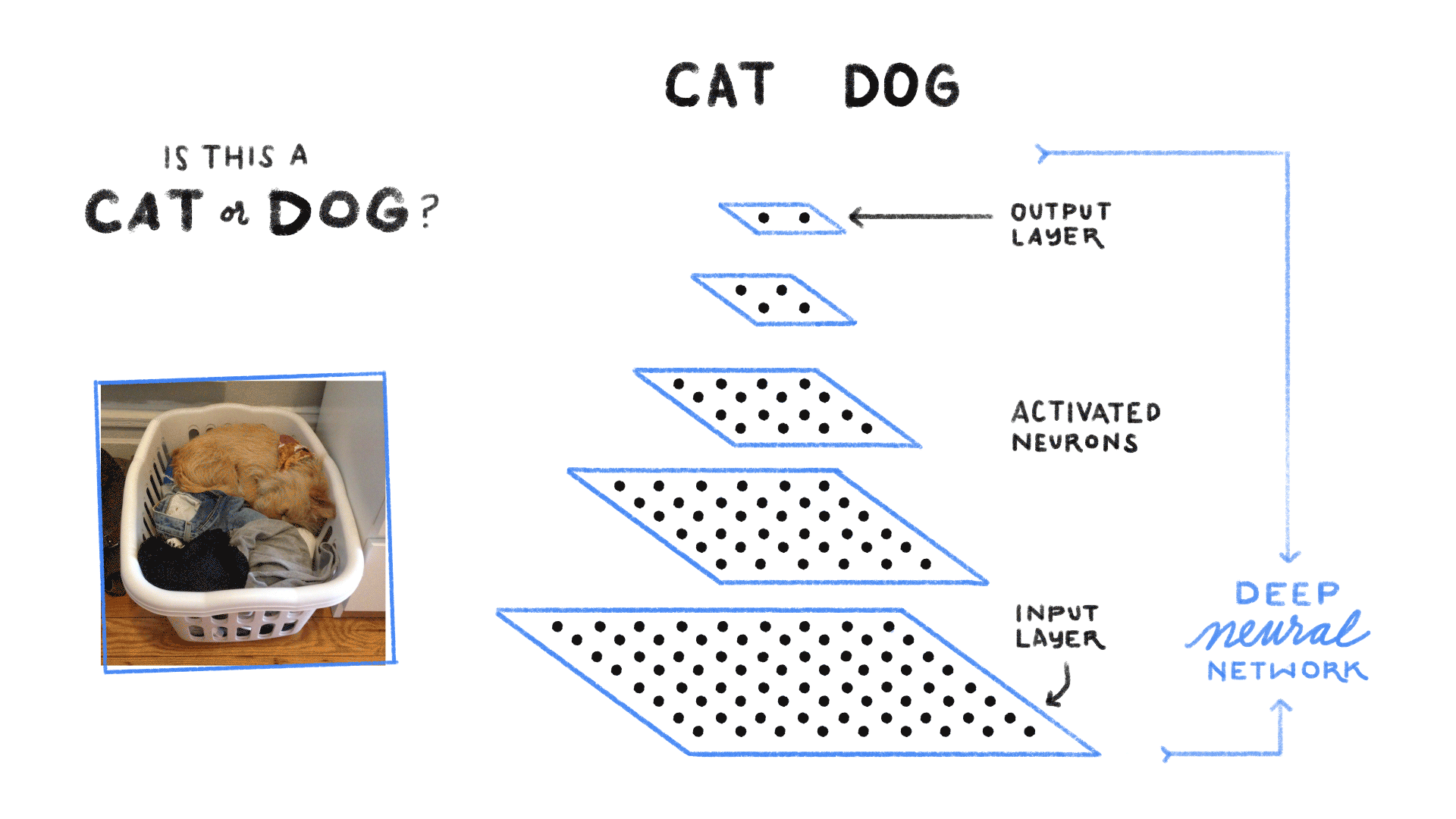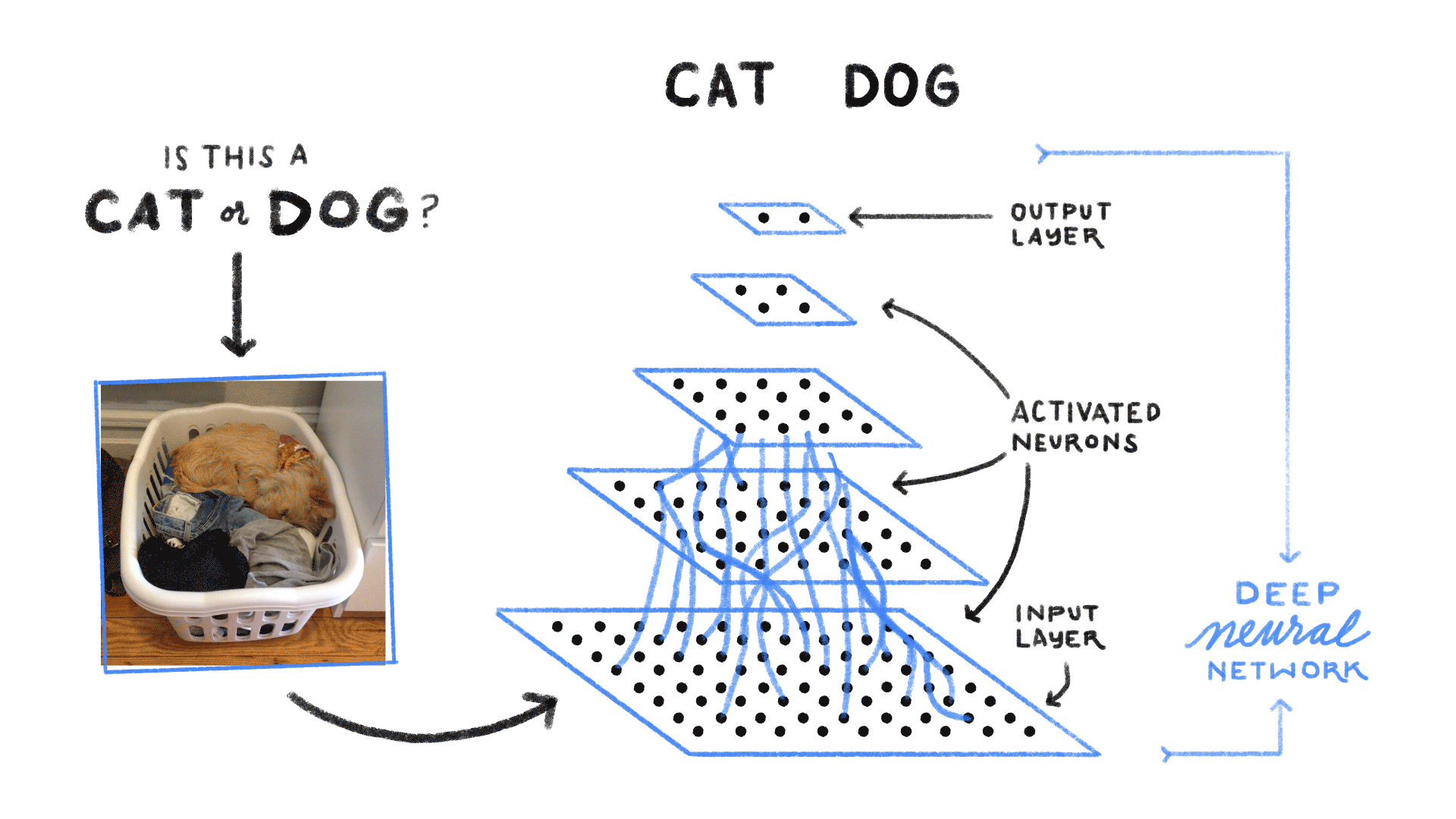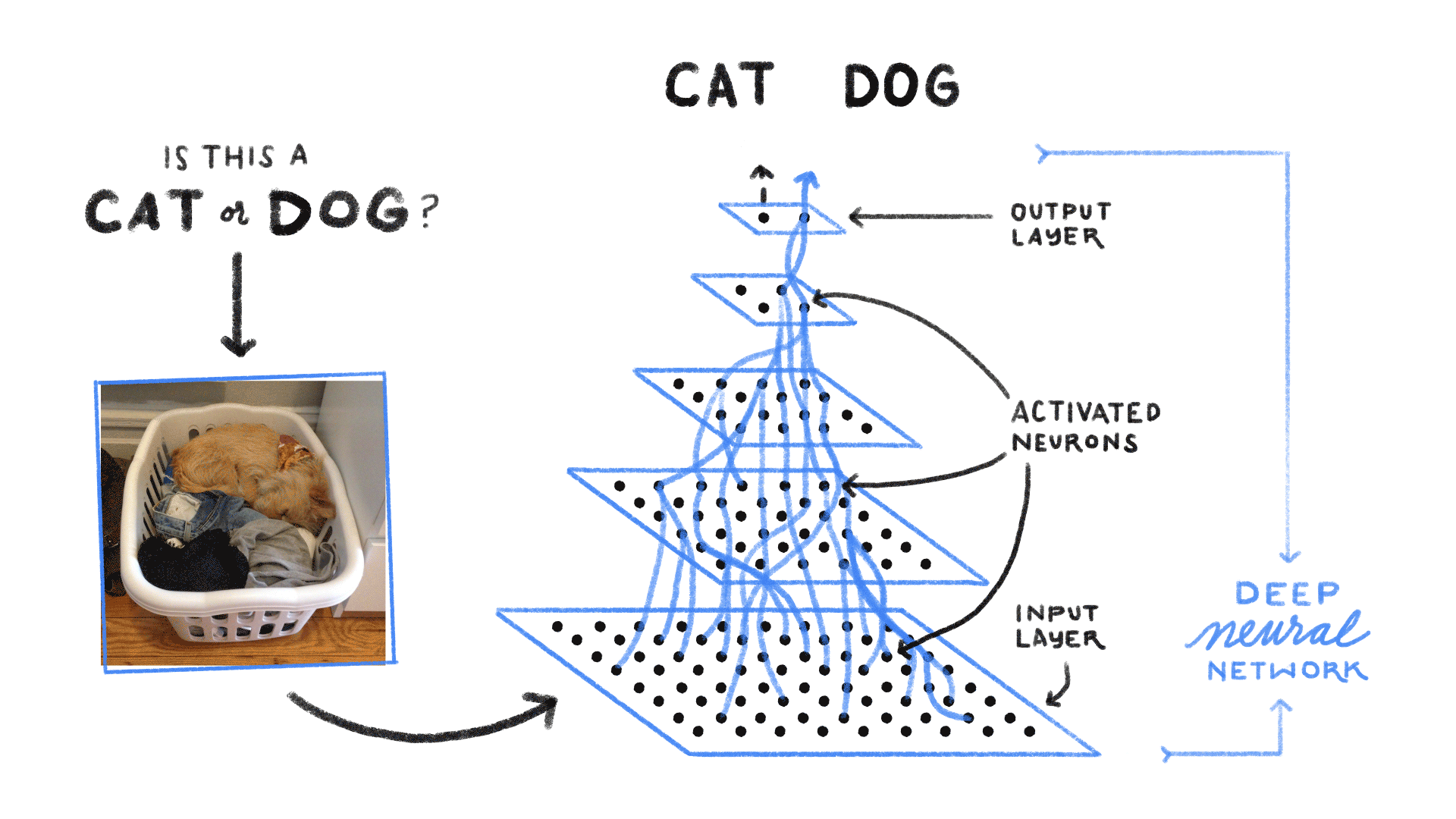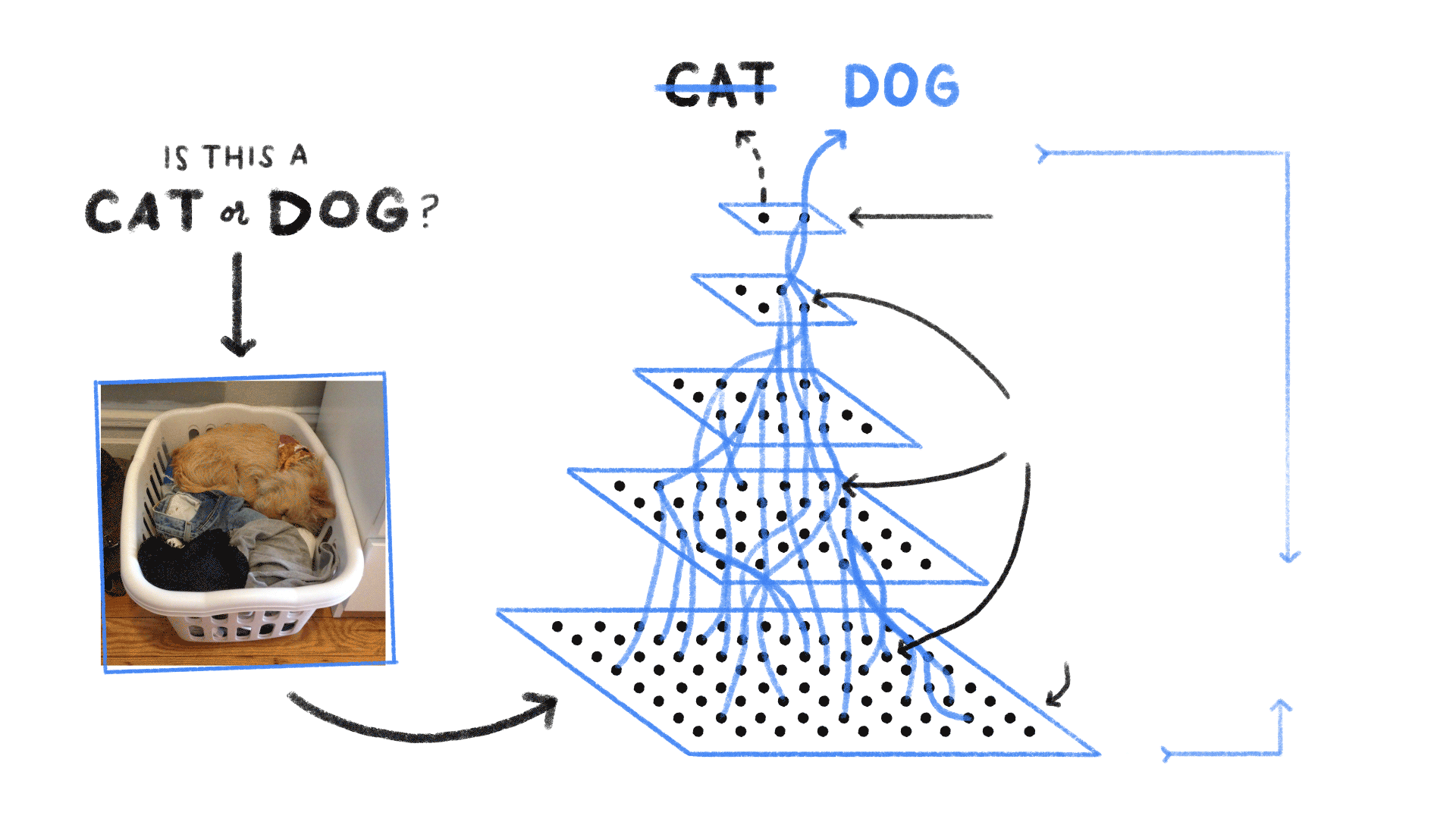
上图卷积神经网络可大致看作是含有三个隐藏层的多层感知机。其中三个激活函数必须均为非线性函数

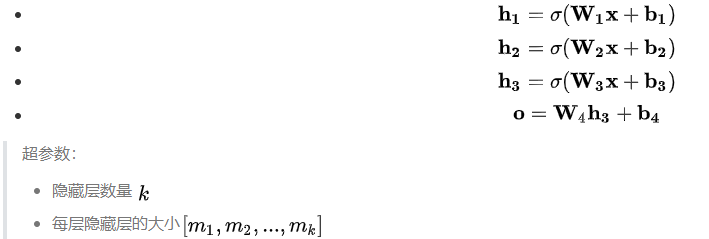
一般每个隐藏层大小是逐层递减的，此处一个可解释性是多层感知机相当于对信息做逐层“压缩”，即对知识做蒸馏，Distillation）

多层感知机的代码实现

• 导入包

import torch
from torch import nn
from d2l import torch as d2lbatch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

• 设置各层参数

一般选用 2 的幂次作为隐藏层数量，因为内存在硬件中的分配和寻址方式，这么做往往可以在计算上更高效。

Parameters()指定 input(Tensor)作为模型参数。

torch.randn(m.n)返回符合随机正态分布的 m*n 张量

# 实现一个具有单隐藏层的多层感知机，它包含256个隐藏单元
num_inputs, num_outputs, num_hiddens = 784, 10, 256# 将网络定义为 nn.Module 子类
class MLP(nn.Module):def __init__(self):super().__init__()self.W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True))self.b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))self.W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True))self.b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))# 定义感知机网络和训练模型def forward(self, X):X = X.reshape((-1, num_inputs))H = relu(X @ self.W1 + self.b1)return (H @ self.W2 + self.b2)

• 定义 ReLU 激活函数

def relu(X):a = torch.zeros_like(X)   #_like(X)表示与输入X的形状相同return torch.max(X,a)

# 创建网络实例
net = MLP()
# 损失
loss = nn.CrossEntropyLoss()

• 训练

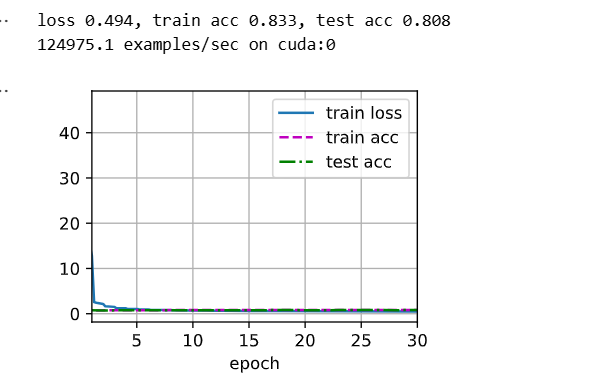
num_epochs, lr = 30, 0.1
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

• 简易实现

import torch
from torch import nn
from d2l import torch as d2l# 隐藏层包含256个隐藏单元，并使用了ReLU激活函数
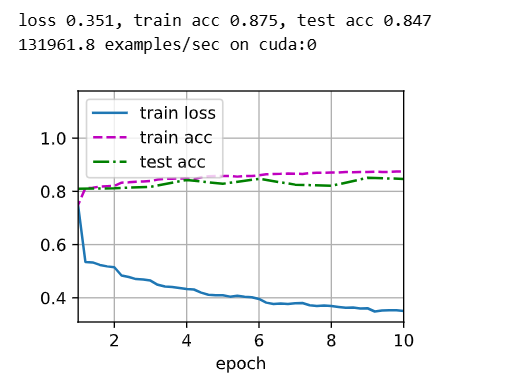
net = nn.Sequential(nn.Flatten(),nn.Linear(784,256),nn.ReLU(),nn.Linear(256,10))def init_weights(m):if type(m) == nn.Linear:nn.init.normal_(m.weight,std=0.01)net.apply(init_weights)# 训练过程
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(), lr=lr)train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

8.模型选择+过拟合欠拟合

模型选择

• 训练误差：模型在训练数据上的误差
• 泛化误差：模型在新数据上的误差
• 训练数据集（Training Dataset）：用于训练模型参数
• 验证数据集（Validation Dataset）：一个用来评估模型好坏的数据集。用来选择、调整模型超参数
  • 例如取出 50%的训练数据作为验证数据
  • 不要与训练数据混用（常犯错误），因为验证数据没有参与模型训练，可以反映出超参数好坏（当数据量不够时，可以采取下文的 k-折交叉验证来构造）
• 测试数据集（Testing Dataset）：只用一次的数据集。（不能用来调整超参数）

K-折交叉验证（K-Fold Cross Validation）

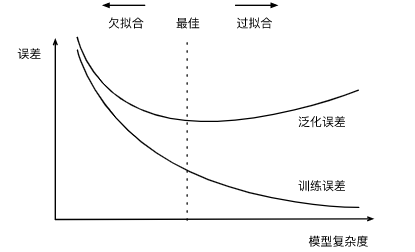
过拟合和欠拟合(overfitting and underfitting)

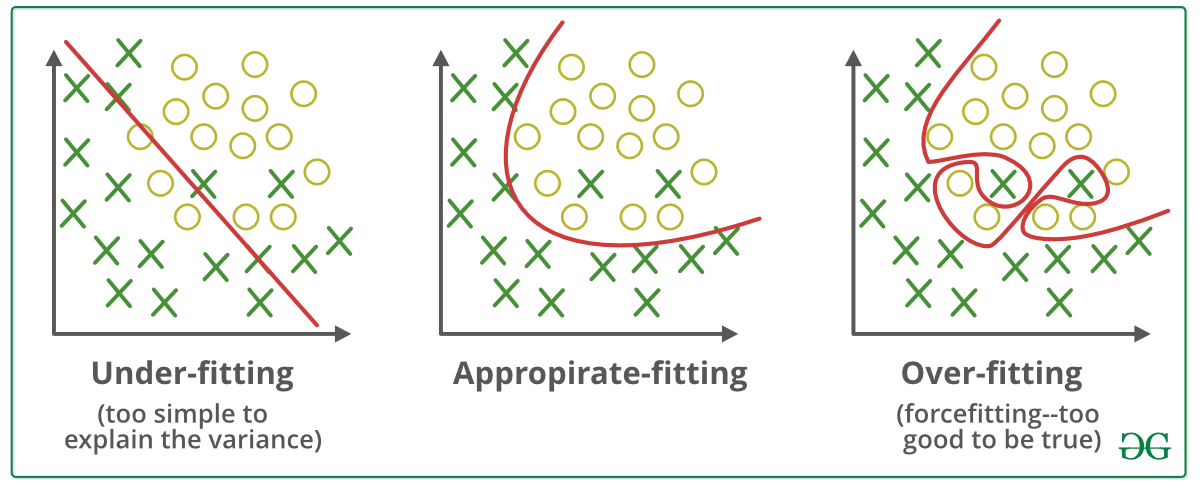
	简单数据	复杂数据
低模型复杂度	正常	欠拟合
高模型复杂度	过拟合	正常

模型复杂度（即：模型容量）：拟合各种函数的能力

模型复杂度要与数据复杂度相匹配。

• 高模型复杂度的模型去训练简单数据，会造成特征过度提取，过分关注噪音，容易“记住”所有训练数据，而丧失泛化性；
• 低模型复杂度的模型去训练复杂数据，会造成无法提取有效特征

一般我们使用泛化误差和训练误差的差值作为模型是否欠拟合、过拟合的衡量

要旨在于，首先保证模型容量，再控制精度，可能会承受一定轻微的过拟合。

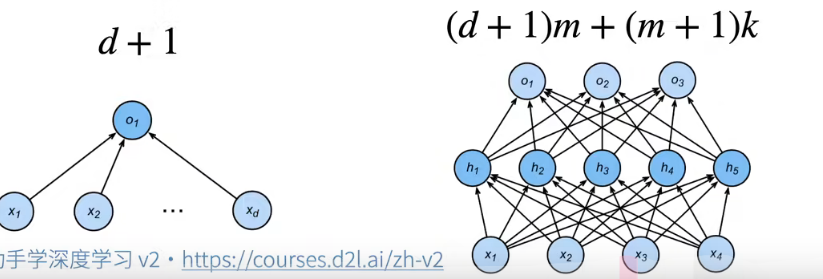
估计模型容量

• 难以在不同种类算法之间比较，例如树模型和神经网络。
• 给定一个模型种类，将有两个主要因素：
  • 参数的个数
  • 参数值的选择范围

VC 维

• 统计学习理论的一个核心思想
• 对一个分类模型，VC 维等于一个最大的数据集大小，不管如何给定标号，都存在一个模型来对它进行完美分类

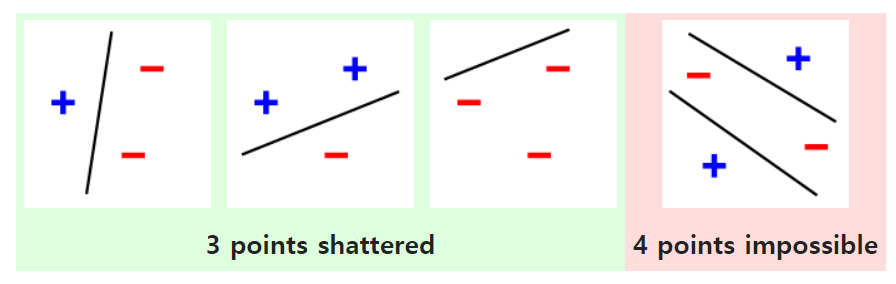
例如，2 维输入的感知机， VC 维=3，即能够分类任何三个点，但不是四个(XOR)。

支持 N 维输入的感知机 VC 维是 N+1

一些多层感知机的 VC 维是

VC 维的用处

• 提供了为什么一个模型好的理论依据，可以衡量训练误差和泛化误差之间的间隔。
• 但深度学习中很少使用：
  • 衡量不是很准确
  • 计算深度学习模型的 VC 维很困难

数据复杂度

• 样本个数
• 每个样本的元素个数（张量的维度和大小）
• 时间、空间结构（图片的空间结构、视频的时间空间维度）
• 多样性（如分几类）

统计学提供了一些理论依据，实际要靠训练/泛化误差对比

代码实例

用阶乘作为分母抵消求导系数的影响。

• 创建数据集

import numpy as np
import math
import torch
from torch import nn
from d2l import torch as d2l
# 多项式的最大阶数
max_degree = 20
# 训练集和测试集的大小
n_train, n_test = 100, 100
# 分配大量的空间
true_w = np.zeros(max_degree)
#其余w=0，噪音项，即一个20维的向量，只有前四项有实值
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])# size=(200, 1)返回一个长度200的列向量
features = np.random.normal(size=(n_train + n_test, 1))
np.random.shuffle(features)# np.power(a,b)返回幂指数a^b,如果是两个不同维度的数组，使用广播法则。
# (200,1)^(1,20)=(200,20)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))for i in range(max_degree):#对其进行gamma函数变换，可以视作阶乘gamma(z)=(z-1)!poly_features[:, i] /= math.gamma(i + 1)labels = np.dot(poly_features, true_w)  # (200,20)*(20,1)=(200,1)
labels += np.random.normal(scale=.1, size=labels.shape)# 使用列表推导将所有数值转换为Tensor类型
true_w, features, poly_features, labels = [torch.tensor(x, dtype=torch.float32) for x in [true_w, features, poly_features, labels]]features[:2], poly_features[:2, :], labels[:2]

• 训练

def evaluate_loss(net, data_iter, loss):'''评估给定数据集上模型的损失'''metric = d2l.Accumulator(2)  #损失的总和，样本数量for X, y in data_iter:# 前向传播得到预测结果out = net(X)#把y和y_hat形状统一y = y.reshape(out.shape)# 计算损失l = loss(out, y)metric.add(l.sum(), l.numel())return metric[0] / metric[1]

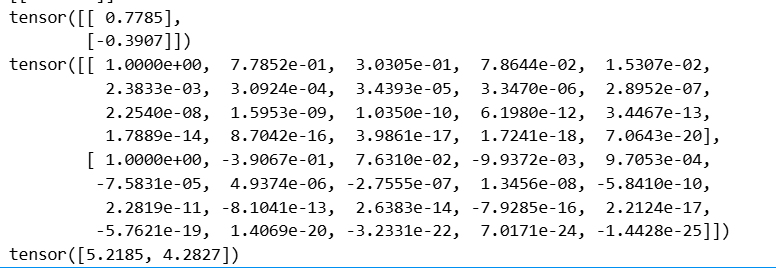
def train(train_features, test_features, train_labels, test_labels,num_epochs=400):loss = nn.MSELoss(reduction='none') #损失不求平均# 输入数据的维数,线性模型是4阶，欠拟合<4，过拟合>4input_shape = train_features.shape[-1] #.shape是返回的是(m,n)的元组，所以-1代表列所对应元素n。net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))batch_size = min(10, train_labels.shape[0])# 两个数据源分别作为提取源，每次批量=batch_size# 把labels变成二维矩阵，与features统一维度，从而提取。# is_train表示用于训练。train_iter = d2l.load_array((train_features, train_labels.reshape(-1,1)),batch_size)test_iter = d2l.load_array((test_features, test_labels.reshape(-1,1)),batch_size, is_train=False)trainer = torch.optim.SGD(net.parameters(), lr=0.001)animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',xlim=[1, num_epochs], ylim=[1e-3, 1e2],legend=['train', 'test'])for epoch in range(num_epochs):d2l.train_epoch_ch3(net, train_iter, loss, trainer)if epoch == 0 or (epoch + 1) % 20 == 0: #每20个epoch绘制一个数据点。animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),evaluate_loss(net, test_iter, loss)))print('weight:', net[0].weight.data.numpy())    # net[0]就是nn.Linear模块

正常拟合：选取数据集前 4 列

'''
定义完训练函数，接着从多项式特征数据中选择前4个维度进行训练，即1,x,x^2/2!,x^3/3!
'''
# 三阶多项式函数拟合(正态)
train(poly_features[:n_train,:4],poly_features[n_train:,:4],labels[:n_train],labels[n_train:])  # 最后返回的weight值和公式真实weight值很接近       

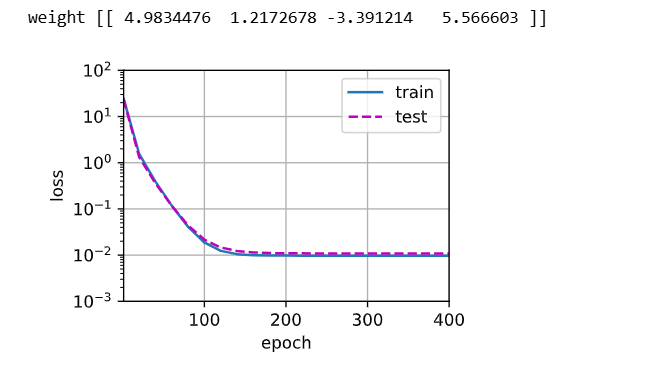
欠拟合：只选取数据集前两列

# 一阶多项式函数拟合(欠拟合)
# 这里相当于用一阶多项式拟合真实的三阶多项式，欠拟合了，损失很高，根本就没降
train(poly_features[:n_train,:2],poly_features[n_train:,:2],labels[:n_train],labels[n_train:])

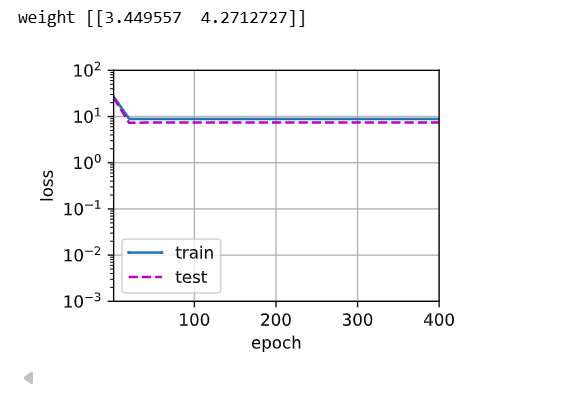
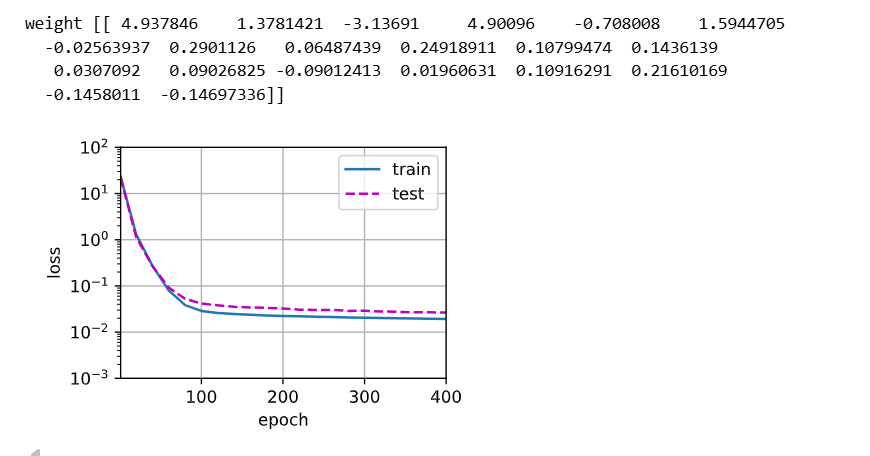
过拟合：选取所有数据集

# 十九阶多项式函数拟合(过拟合)
# 这里相当于用十九阶多项式拟合真实的三阶多项式，过拟合了
train(poly_features[:n_train,:],poly_features[n_train:,:],labels[:n_train],labels[n_train:])

Q&A🤓

Q：SVM（支持向量机）在分类任务中效果也可以，但为什么不如神经网络应用广泛？

�‍*♂️**：一个原因是传统机器学习算法如 SVM（或者 kernal SVM）在小数据集上训练还是可以，但数据量大时，训练就会比较困难。而且 SVM 可调的超参数不多、Kernal 的不同选择对结果区别不明显。另一个原因如沐神所说，神经网络相当于一个“语言”，可以针对不同任务，进行灵活的组合变化，可编程性很强，目前大多数深度学习框架也都是“图灵完备（Turing Complete）”语言，可以解决所有的可计算问题。同时神经网络是一种“端到端学习（End-to-End Learning）”，比如对于图片分类任务，SVM 还需要专门设计特征提取器和分类器，而神经网络可以在一种架构下同时具备这两个功能。

Q：一般训练、测试、验证三个数据集的划分标准是什么？

�‍*♂️**：一般情况划分总数据的 30%作为测试数据，总数据的 70%作为训练数据，同时在训练数据上做 5-折交叉验证，如果数据足够大，可以五五开分割测试和训练数据集，同时在训练数据集做 k-折交叉验证。

Q：对于分类问题，如果数据集中各类数量很不平衡，那么在构造验证数据集的时，各类数量应保持与原始数据集相似的不平衡比例，还是均衡各类比例？

�‍*♂️**：在验证数据集上还是要均衡各类比例，这样可以避免模型存在“偏好”问题。（比如二分类问题，正负样本比例为 90%：10%，如果验证数据集保持 9：1 比例，则哪怕模型全部判正类，在此验证数据集上也会获得 90%的精度，这是不正确的）。

解决方法是首先评估数据集不平衡性和真实世界的情况是否吻合，如果真实世界也是如此不平衡，那模型专注于做好主流分类就 Ok；如果只是数据集采样导致不平衡，则可以通过增加少样本的权重来增大重要性（比如复制多份、在 Loss 函数里加权等等）。

Q：沐神对于当下深度学习的感受经典定义

�‍*♂️**：“大家希望深度学习是一门‘科学👨‍🎓’，但实际上是一门‘工程👨‍🔧’，其中 50%还是‘艺术👨‍🎨’”。

9.权重衰退(Weight Decay)

权重衰退的核心思想是惩罚大权重，避免模型在训练数据上过度拟合。通过对每个权重的平方加一个正则化项，迫使网络在学习时倾向于使用更小的权重。这样可以有效控制模型的复杂度，防止模型在训练数据上表现得过好，但在测试数据上效果不佳(即过拟合)

最常见的处理过拟合的方法。 权重衰减本质上就是在损失函数中加入L2正则化项

如何控制模型容量？

使用均方范数作为硬性限制条件

但一般不采用，因为该定义不好做优化（已有的优化算法无法处理这一硬性条件）

使用均方范数作为柔性限制

为解决上个方法不好优化的问题，可将硬性条件形式化到损失函数中。

图片解释：同心圆代表损失函数的等高线，则等高线中心代表未加正则项的最小损失点，而正则项
代表的等高线为图中以原点为圆心的阴影圆，其最小惩罚值在坐标轴原点。则在图中必存在一个平衡点，使得损失+正则惩罚值最小

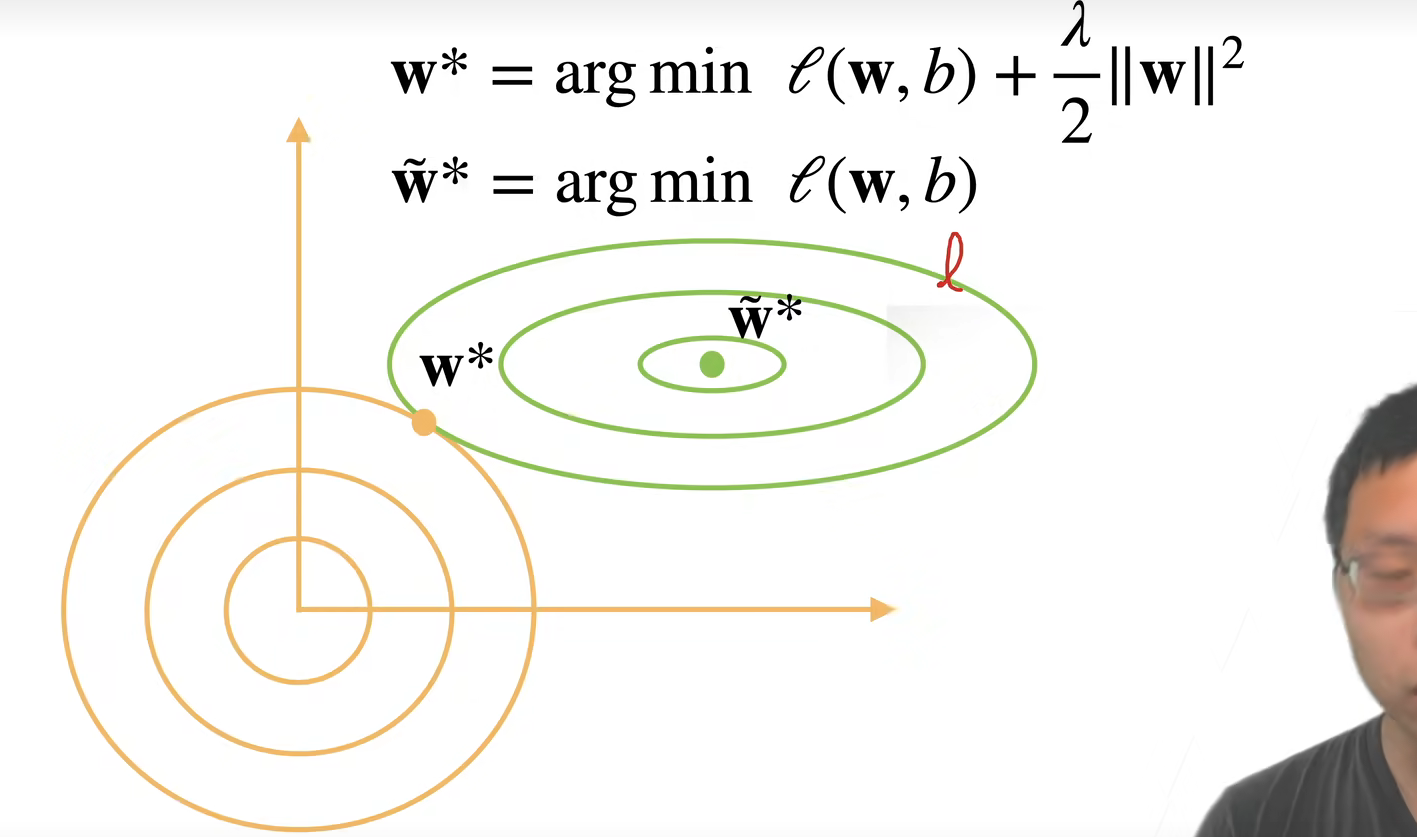
参数更新法则

权重衰退通过 L2 正则项使得模型参数不会过大，从而控制模型复杂度。正则项权重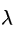
是控制模型复杂度的超参数。

权重衰退的代码实现

首先生成一个人工数据集，依据：

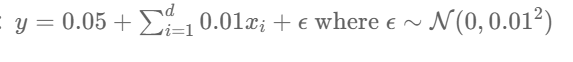
• 创建数据集

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
# 训练集n_train越小，越容易过拟合；同理，输入特征num_inputs越多，模型越复杂
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5 # 数据越简单，模型越复杂，越容易过拟合。num_inputs为特征维度
true_w, true_b = torch.ones((num_inputs,1)) * 0.01, 0.05
# synthetic_data()函数返回y=wx+b+noise，n_train表示执行此任务的样本数量，这个函数已经考虑了噪音。
train_data = d2l.synthetic_data(true_w, true_b, n_train) # 生成人工数据集
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)

• 初始化模型参数和L2惩罚
• 
• 

def init_params():w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)b = torch.zeros(1, requires_grad=True)return [w, b]                                             

• 定义L2范数惩罚

def l2_penalty(w):return torch.sum(w.pow(2)) / 2  # .pow()函数代表指数运算符

• 定义训练函数

# 训练一个线性回归模型，并在训练中加入 L2 正则化（权重衰减），同时用 Animator 实时画出训练集与测试集的损失曲线。
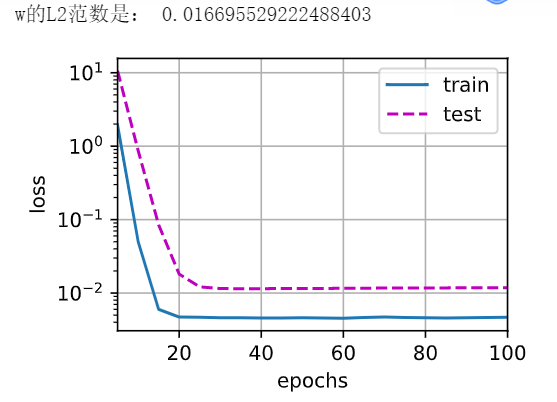
def train(lambd):w, b = init_params()net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_lossnum_epochs, lr = 100, 0.003animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale = 'log',xlim=[5, num_epochs], legend=['train', 'test'])for epoch in range(num_epochs):for X, y in train_iter:#with torch.enable_grad(): 新版不需要这么写l = loss(net(X), y) + lambd * l2_penalty(w)l.sum().backward() #求导已经包括对lambda项的求导d2l.sgd([w, b], lr, batch_size)if (epoch + 1) % 5 == 0:animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),d2l.evaluate_loss(net, test_iter, loss)))print('w的L2范数是：', torch.norm(w).item())  #返回值是一个tensor，所以要用item()调用元素。#只有一维张量可以返回一个标量，因为本身就是一个标量，只是改了数据类型。

• 分不同数值训练

# 忽略正则化直接训练
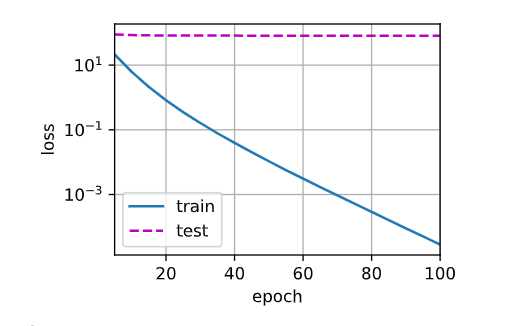
train(lambd=0)  # 训练集小，过拟合，测试集损失不下降
输出：
w的L2范数是 13.300994873046875

由图形状可知，模型已严重过拟合

train(lambd=3)
# 输出L2范数为：0.3527

由图形状可知，模型过拟合程度减轻

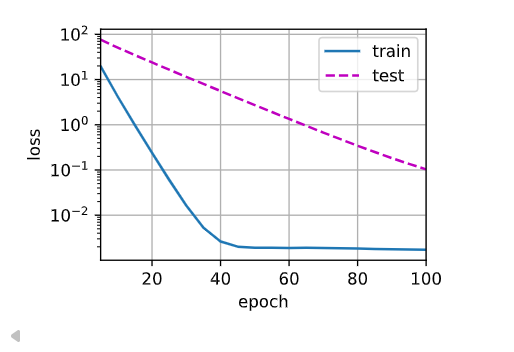
train(lambd=20)

由图可知，此时模型拟合程度比较好

• 简洁实现

# 简洁实现
def train_concise(wd):net = nn.Sequential(nn.Linear(num_inputs,1))for param in net.parameters():param.data.normal_()loss = nn.MSELoss()num_epochs, lr = 100, 0.003# 惩罚项既可以写在目标函数里面，也可以写在训练算法里面，每一次在更新之前把当前的w乘以衰退因子weight_decay trainer = torch.optim.SGD([{"params":net[0].weight,"weight_decay":wd},{"params":net[0].bias}],lr=lr)                     animator = d2l.Animator(xlabel='epoch',ylabel='loss',yscale='log',xlim=[5,num_epochs],legend=['train','test'])                   for epoch in range(num_epochs):for X, y in train_iter:with torch.enable_grad():trainer.zero_grad()l = loss(net(X),y)l.backward()trainer.step()if(epoch + 1) % 5 == 0:animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss), d2l.evaluate_loss(net,test_iter,loss)))print('w的L2范数是',net[0].weight.norm().item()) 

• 训练

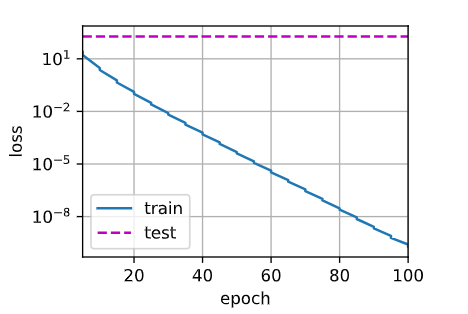
# 这些图看起来和我们从零开始实现权重衰减时的图相同
train_concise(0)
# w的L2范数是 14.216987609863281

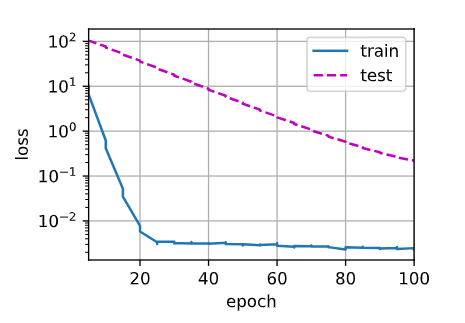
train_concise(3)
# w的L2范数是 0.36535120010375977

10.丢弃法（dropout）

也是一种防止过拟合的方法

丢弃法（Dropout）：训练神经网络时，随机“丢弃”一部分神经元（将一些输出项随机置为0）来控制模型复杂度，强迫模型不能依赖某几个特定的神经元，从而学得更健壮、更有泛化能力。

常用作在多层感知机的隐藏层输出上

丢弃概率是控制模型复杂度的超参数

动机

• 一个好的模型需要对输入数据的扰动鲁棒（Robust）
  • 使用有噪音的数据等价于Tikhonov 正则（又称：岭回归）
  • 丢弃法：相当于在层之间加入噪音。

无偏差的加入噪音

相当于有一定概率 p 使一个值变为零，否则使之变大。这种定义下，可保证期望E不变

使用丢弃法训练过程

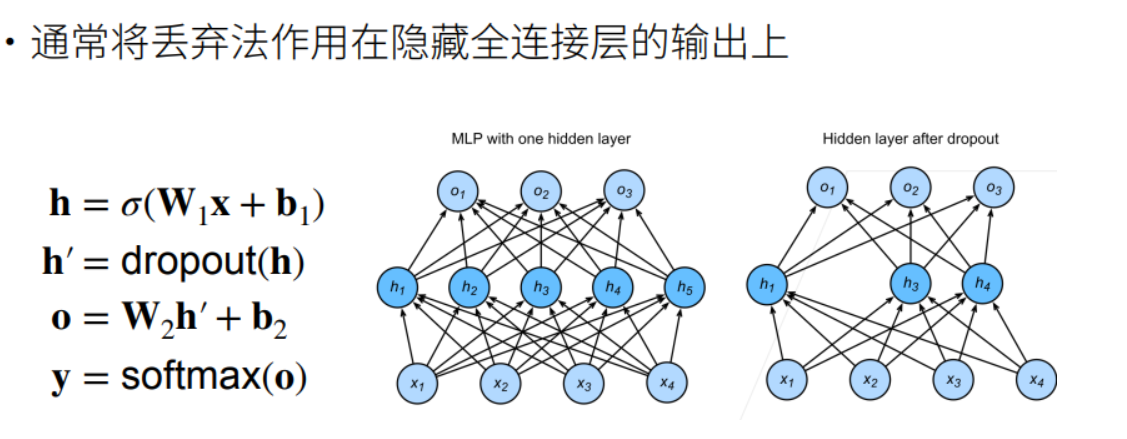
• 丢弃概率p是控制模型复杂度的超参数，p越大，模型复杂度越小，反之亦然
• 一般只用于全连接神经网络（多层感知机），而权重衰退（Weight Decay）通用性更强
• 一般可以将模型复杂度设置得大一些（比如隐藏层数量更多、隐藏层更大），再添加 Dropout 操作，效果可能会好于一个无 Dropout 的稍简单的网络

推理（预测）中的丢弃法

• 正则项只在训练中使用：他们影响模型参数的更新
• 在推理过程中，丢弃法直接返回输入

这样也能保证预测时模型结构的固定，有确定性的输出，否则模型结构将会发生随机改变，导致结果不可控。

当年 Hinton 老爷子认为，dropout 相当于每一次采样一个子神经网络做集成训练。在后来人们的研究中，Dropout 表现出的效果更像是一个正则项。

代码实现

• 定义 dropout 函数，该函数以dropout的概率丢弃张量输入x中的元素

# 实现dropout_layer函数，该函数以dropout的概率丢弃张量输入x中的元素
import torch
from torch import nn
from d2l import torch as d2ldef dropout_layer(X, dropout):assert 0 <= dropout <= 1 # dropout大于等于0，小于等于1，否则报错if dropout == 1:return torch.zeros_like(X) # 如果dropout为1，则X返回为全0if dropout == 0:return X # 如果dropout为0，则X返回为全原值
# mask 是一个与输入X形状相同的张量，里面只包含0和1，用来随机决定每个神经元是否被“保留”或“丢弃”mask = (torch.rand(X.shape, device=X.device) > dropout).float()return mask * X / (1.0 - dropout) X = torch.arange(16,dtype=torch.float32).reshape((2,8))
print(X)
print(dropout_layer(X, 0.))
print(dropout_layer(X, 0.5)) # 有百分之50的概率变为0
print(dropout_layer(X, 1.))输出：
tensor([[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.],[ 8.,  9., 10., 11., 12., 13., 14., 15.]])
tensor([[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.],[ 8.,  9., 10., 11., 12., 13., 14., 15.]])
tensor([[ 0.,  0.,  4.,  6.,  0.,  0.,  0.,  0.],[16.,  0., 20., 22., 24., 26.,  0., 30.]])
tensor([[0., 0., 0., 0., 0., 0., 0., 0.],[0., 0., 0., 0., 0., 0., 0., 0.]])

• 定义模型

# 定义具有两个隐藏层的多层感知机，每个隐藏层包含256个单元
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10 ,256, 256
dropout1, dropout2 = 0.2, 0.5class Net(nn.Module):def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,is_training=True):       super(Net, self).__init__()self.num_inputs = num_inputsself.training = is_trainingself.lin1 = nn.Linear(num_inputs, num_hiddens1)self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)self.lin3 = nn.Linear(num_hiddens2, num_outputs)self.relu = nn.ReLU()def forward(self, X):H1 = self.relu(self.lin1(X.reshape((-1,self.num_inputs))))if self.training == True: # 如果是在训练，则作用dropout，否则则不作用H1 = dropout_layer(H1, dropout1)H2 = self.relu(self.lin2(H1))if self.training == True:H2 = dropout_layer(H2,dropout2)out = self.lin3(H2) # 输出层不作用dropoutreturn outnet = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)

• 训练

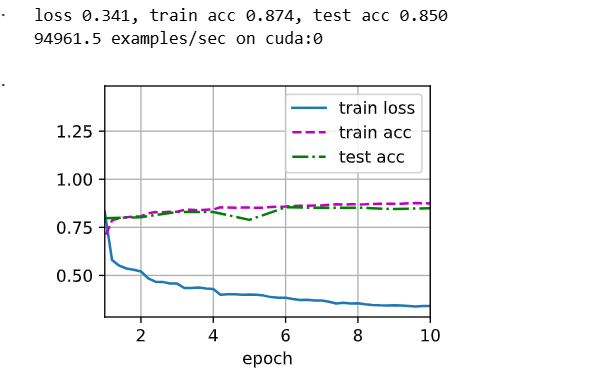
num_epochs, lr, batch_size = 10, .5, 256
loss = nn.CrossEntropyLoss()    #打包了softmaxtrain_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)  #net.parameters(recurse=True)返回模块和所有子模块的参数。d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

• 简洁实现

import torch
from torch import nn
from d2l import torch as d2l# 简洁实现
num_epochs, lr, batch_size = 10, 0.5, 256
dropout1, dropout2 = 0.2, 0.5
loss = nn.CrossEntropyLoss()
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)net = nn.Sequential(nn.Flatten(),              # 1️ 展平层nn.Linear(784, 256),       # 2️ 全连接层1（输入784 -> 输出256）nn.ReLU(),                 # 3️ 激活函数ReLUnn.Dropout(dropout1),      # 4️ Dropout层（丢弃比例 = dropout1）nn.Linear(256, 256),       # 5️ 全连接层2nn.ReLU(),                 # 6️ 激活函数ReLUnn.Dropout(dropout2),      # 7️ Dropout层（丢弃比例 = dropout2）nn.Linear(256, 10)         # 8️ 输出层（10类分类）
)def init_weights(m):
# 如果是线性层,初始化权重参数,均值为 0、标准差为 0.01 的正态分布随机数来填充if type(m) == nn.Linear:nn.init.normal_(m.weight,std=0.01)net.apply(init_weights)
# 使用 随机梯度下降（SGD） 优化算法，以学习率 lr 更新网络 net 中所有需要训练的参数
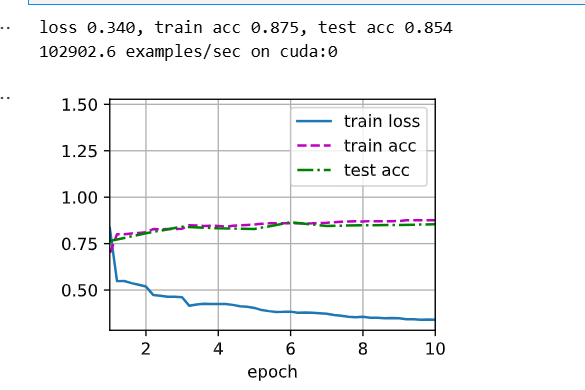
trainer = torch.optim.SGD(net.parameters(),lr=lr)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

nn.Dropout模块在评估（推理）时，会自动停止 Dropout 操作

Q&A

Q：Dropout 在训练的时候进行随机丢弃，在推理的时候又都不丢弃，这样在预测时候，不就相当于还在一个“可能”过拟合的网络结构上使用（所有神经元都为可用）？

�‍*♂️**：关于这点，可以点击以下视频 👇 观看吴恩达 DeepLearning.ai 中一节课程《Why does Dropout work？》

大致观点是，Dropout 在训练过程中，通过随机置零神经元结构，使得 Dropout 下层神经元不能过分依赖上层的某些输入，而不得不 Spread out 权重，这会导致权重收缩（Shrink Weights），从而达到和 L2 正则一样的效果。

结合吴恩达的观点，私以为神经网络在预测时虽然网络结构依旧完整（相比训练时，反而可用的神经元更多），但经过 Dropout 训练时的“调教”，使得神经元权重分配更加“合理”，不会过分地关注某些特征而造成过拟合，同时在数学上相当于增加了正则项，所以限制了模型复杂度。

Q：Dropout和前一节的权重衰退等正则化方法相比具体有什么关系？有没有一个综述性的对比讲解？

�‍♂️：Of Course！在我们笔记主页推荐过的博客*TheAISummer**上有一篇综述性文章可供参考👉Regularization techniques for training deep neural networks

11.kaggle加州房价预测案例

本节我们将详细介绍数据预处理、模型设计和超参数选择。 通过亲身实践，你将获得一手经验，这些经验将指导你数据科学家职业生涯。

该比赛项目网址：点击 👉这里，数据描述：点击 👉这里

BN 是 Batch Normalization（批量归一化)

代码实现

import hashlib
import os
import tarfile
import zipfile
import requests
import numpy as np
import pandas as pd
import torch
from torch import nn
from d2l import torch as d2l
%matplotlib inlineDATA_HUB = dict()
DATA_URL = 'http://d2l-data.s3-accelerate.amazonaws.com/'def download(name, cache_dir=os.path.join('.', '01_data/02_DataSet_Kaggle_House')):"""下载一个DATA_HUB中的文件，返回本地文件名"""assert name in DATA_HUB, f"{name} 不存在于 {DATA_HUB}."url , sha1_hash = DATA_HUB[name]os.makedirs(cache_dir, exist_ok=True)fname = os.path.join(cache_dir, url.split('/')[-1])if os.path.exists(fname):sha1 = hashlib.sha1()with open(fname,'rb') as f:while True:data = f.read(1048576)if not data:breaksha1.update(data)if sha1.hexdigest() == sha1_hash:return fnameprint(f'正在从{url}下载{fname}...')r = requests.get(url,stream=True,verify=True)with open(fname,'wb') as f:f.write(r.content)return fnamedef download_extract(name, folder=None):"""下载并解压zip/tar文件"""fname = download(name)base_dir = os.path.dirname(fname)data_dir, ext = os.path.splitext(fname)if ext == '.zip':fp = zipfile.ZipFile(fname, 'r')elif ext in ('.tar', '.gz'):fp = tarfile.open(fname, 'r')else:assert False, '只有zip/tar文件可以被解压缩'fp,extractall(base_dir)return os.path.join(base_dir, folder) if folder else data_dirdef download_all():"""下载DATA_UHB中的所有文件"""for name in DATA_HUB:download(name)DATA_HUB['kaggle_house_train'] = (DATA_URL + 'kaggle_house_pred_train.csv','585e9cc9370b9160e7921475fbcd7d31219ce')         
DATA_HUB['kaggle_house_test'] = (DATA_URL + 'kaggle_house_pred_test.csv', 'fal9780a7b011d9b009e8bff8e99922a8ee2eb90')     
train_data = pd.read_csv(download('kaggle_house_train'))
test_data = pd.read_csv(download('kaggle_house_test'))
print(train_data.shape) # 1460个样本，80个te特征，1个标号label
print(test_data.shape) # 测试样本没有标号labelprint(train_data.iloc[0:4,[0,1,2,3,-3,-2,-1]]) # 前面四行的某些列特征

# 在每个样本中，第一个特征是ID，将其从数据集中删除  
all_features = pd.concat((train_data.iloc[:,1:-1],test_data.iloc[:,1:])) # 从第2列开始，第1列没有了 
print(all_features.iloc[0:4,[0,1,2,3,-3,-2,-1]])

# 将所有缺失的值替换成相应特征的平均值
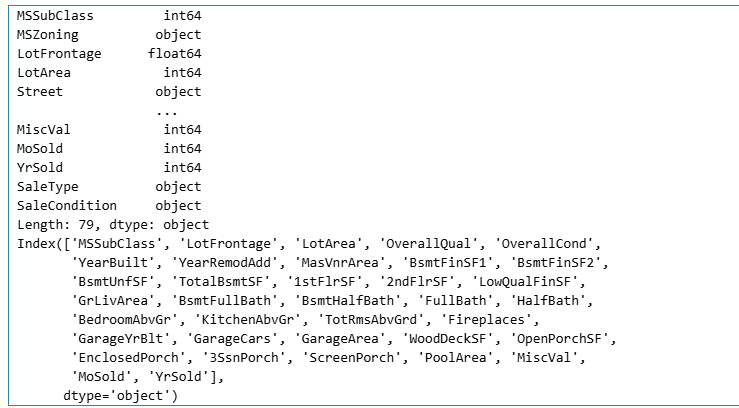
# 通过将特征重新缩放到零均值和单位方差来标准化数据
print(all_features.dtypes) # 可以知道每一列分别为什么类型特征
numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index  # 当值的类型不是object的话，就是一个数值
print(numeric_features)
all_features[numeric_features] = all_features[numeric_features].apply(lambda x: (x - x.mean()) / (x.std())) # 对数值数据变为总体为均值为0，方差为1的分布的数据        
all_features[numeric_features] = all_features[numeric_features].fillna(0)  # 将数值数据中not number的数据用0填充      

# 处理离散值。用一次独热编码替换它们
# 若一列里面有五个不同的值，则创建五个features，如果该列中为该feature则为1，不为该feature则为0
all_features = pd.get_dummies(all_features,dummy_na=True) 
all_features.shape  # (2919, 330)

# 从pandas格式中提取Numpy格式，并将其转换为张量表示
print(train_data.shape)  #(1460, 81)
n_train = train_data.shape[0] # 样本个数# 确保数据是数值类型
train_features = torch.tensor(all_features[:n_train].values.astype(np.float32),dtype=torch.float32)
test_features = torch.tensor(all_features[n_train:].values.astype(np.float32),dtype=torch.float32)
# train_data的SalePrice列是label值
train_labels = torch.tensor(train_data.SalePrice.values.reshape(-1,1),dtype=torch.float32)

# 训练
loss = nn.MSELoss()
print(train_features.shape[1]) # 所有特征个数,330
in_features = train_features.shape[1]
def get_net():net = nn.Sequential(nn.Linear(in_features,1)) # 单层线性回归return net

def log_rmse(net, features, labels):clipped_preds = torch.clamp(net(features),1,float('inf')) # 把模型输出的值限制在1和inf之间，inf代表无穷大（infinity的缩写）       rmse = torch.sqrt(loss(torch.log(clipped_preds),torch.log(labels))) # 预测做log，label做log，然后丢到MSE损失函数里return rmse.item()

# 训练函数将借助Adam优化器
def train(net, train_features, train_labels, test_features, test_labels,num_epochs, learning_rate, weight_decay, batch_size):train_ls, test_ls = [], []train_iter = d2l.load_array((train_features, train_labels), batch_size)optimizer = torch.optim.Adam(net.parameters(), lr=learning_rate, weight_decay=weight_decay)for epoch in range(num_epochs):for X, y in train_iter:optimizer.zero_grad()l = loss(net(X),y)l.backward()optimizer.step()train_ls.append(log_rmse(net,train_features,train_labels))if test_labels is not None:test_ls.append(log_rmse(net, test_features, test_labels))return train_ls, test_ls

# K折交叉验证
def get_k_fold_data(k,i,X,y): # 给定k折，给定第几折，返回相应的训练集、测试集assert k > 1fold_size = X.shape[0] // k  # 每一折的大小为样本数除以kX_train, y_train = None, Nonefor j in range(k): # 每一折idx = slice(j * fold_size, (j+1)*fold_size) # 每一折的切片索引间隔  X_part, y_part = X[idx,:], y[idx] # 把每一折对应部分取出来if j == i: # i表示第几折，把它作为验证集X_valid, y_valid = X_part, y_partelif X_train is None: # 第一次看到X_train，则把它存起来 X_train, y_train = X_part, y_partelse: # 后面再看到，除了第i外，其余折也作为训练数据集，用torch.cat将原先的合并    X_train = torch.cat([X_train, X_part],0)y_train = torch.cat([y_train, y_part],0)return X_train, y_train, X_valid, y_valid # 返回训练集和验证集

# 返回训练和验证误差的平均值
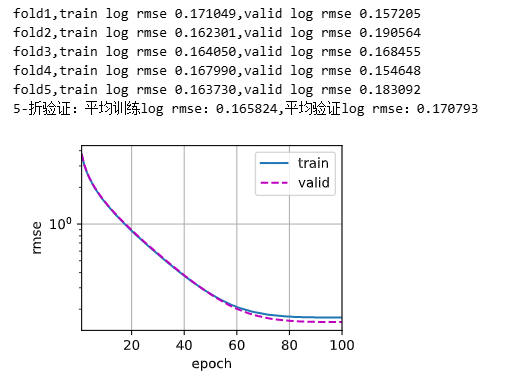
def k_fold(k, X_train, y_train, num_epochs, learning_rate, weight_decay,batch_size):train_l_sum, valid_l_sum = 0, 0for i in range(k):data = get_k_fold_data(k, i, X_train, y_train) # 把第i折对应分开的数据集、验证集拿出来   net = get_net()# *是解码，变成前面返回的四个数据train_ls, valid_ls = train(net, *data, num_epochs, learning_rate, weight_decay, batch_size) # 训练集、验证集丢进train函数 train_l_sum += train_ls[-1]valid_l_sum += valid_ls[-1]if i == 0:d2l.plot(list(range(1, num_epochs + 1)), [train_ls,valid_ls],xlabel='epoch',ylabel='rmse',xlim=[1,num_epochs],legend=['train','valid'],yscale='log')print(f'fold{i+1},train log rmse {float(train_ls[-1]):f},'f'valid log rmse {float (valid_ls[-1]):f}')return  train_l_sum / k, valid_l_sum / k # 求和做平均

# 模型选择
k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
train_l, valid_l = k_fold(k, train_features, train_labels, num_epochs, lr, weight_decay, batch_size)   
print(f'{k}-折验证：平均训练log rmse：{float(train_l):f},'f'平均验证log rmse：{float(valid_l):f}')    

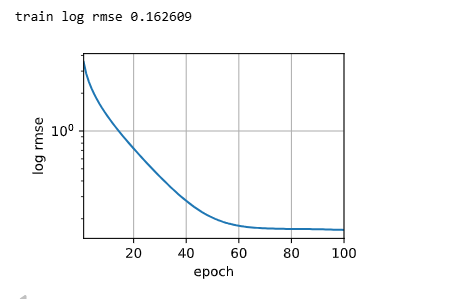
def train_and_pred(train_features, test_feature, train_labels, test_data, num_epochs, lr, weight_decay, batch_size):net = get_net()train_ls, _ = train(net, train_features, train_labels, None, None, num_epochs, lr, weight_decay, batch_size)  d2l.plot(np.arange(1, num_epochs + 1), [train_ls], xlabel='epoch',ylabel = 'log rmse', xlim=[1,num_epochs], yscale='log')print(f'train log rmse {float(train_ls[-1]):f}')preds = net(test_features).detach().numpy()test_data['SalePrice'] = pd.Series(preds.reshape(1,-1)[0])submission = pd.concat([test_data['Id'],test_data['SalePrice']],axis=1)submission.to_csv('submission.csv',index = False)train_and_pred(train_features, test_features, train_labels, test_data,num_epochs, lr, weight_decay, batch_size)

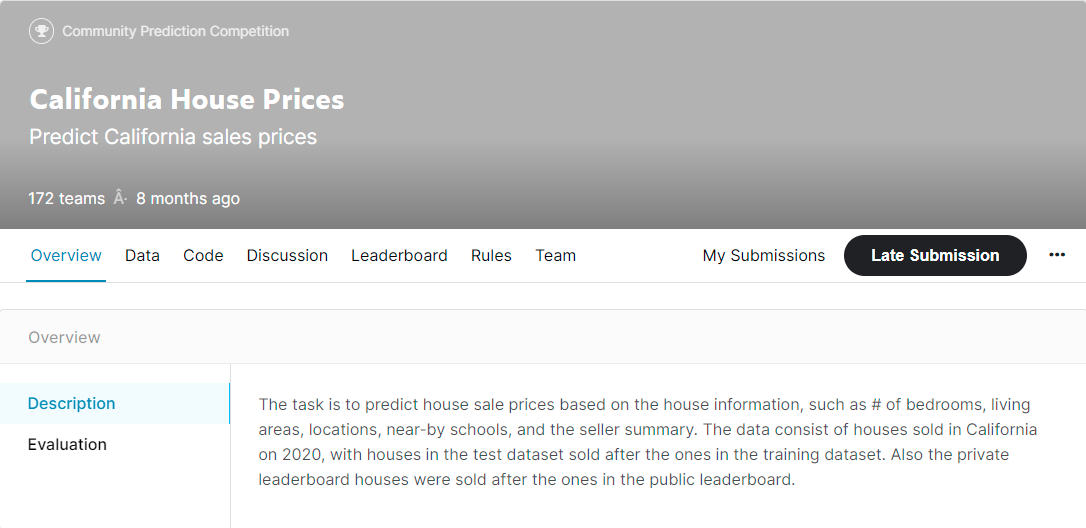
课后作业

本节课最后，李沐老师动员大家去 Kaggle 上做他为课程专门开设的一个小竞赛California House Prices，作为前期学习效果的实践巩固和检验。大家可以点击下图访问查看 👇。目前仍然可以提交成绩，整个数据集大小在 80Mb 左右，涉及 40 个特征，训练数据共 47439 条，测试数据共 31626 条。

Q&A

Q：训练时在做数据特征化时，内存炸掉怎么办？

�‍*♂️**：数据的特征化处理一直也是深度学习乃至机器学习很重要的一步，而一般对于 NLP 领域、CV 领域来说，数据量都很大，常常会遇到还没开始训练，仅特征化数据就炸内存/显存的问题。一般碰到硬件瓶颈时无非就两种途径：

1. 有钱任性上更好、更贵的硬件
2. 改进算法，使计算复杂度、空间复杂度降低

有时候，方法 1 我们心有余而力不足（🚫💰 没钱 or 已经达到当下硬件极限），大多都是通过方法 2 在现有硬件条件下，通过开动脑筋 🙇‍♂️，来达到我们的目的（纵观机器学习的发展史，各种著名的模型算法，如 word bag、word2vec、CNN、LSTM、Transformer 等，都是在现有硬件极限下，通过巧妙地设计，成功处理更大更复杂数据的范例）。

在传统机器学习中，特征工程是决定一项任务成败的关键一环，美国计算机科学家 Peter Norvig 的 2 句经典名言：

基于大量数据的简单模型优于基于少量数据的复杂模型。

这句说明了数据量的重要性。

更多的数据优于聪明的算法，而好的数据优于多的数据。

这句则是说的特征工程的重要性。

所以，如何基于给定数据来发挥更大的数据价值就是特征工程要做的事情。

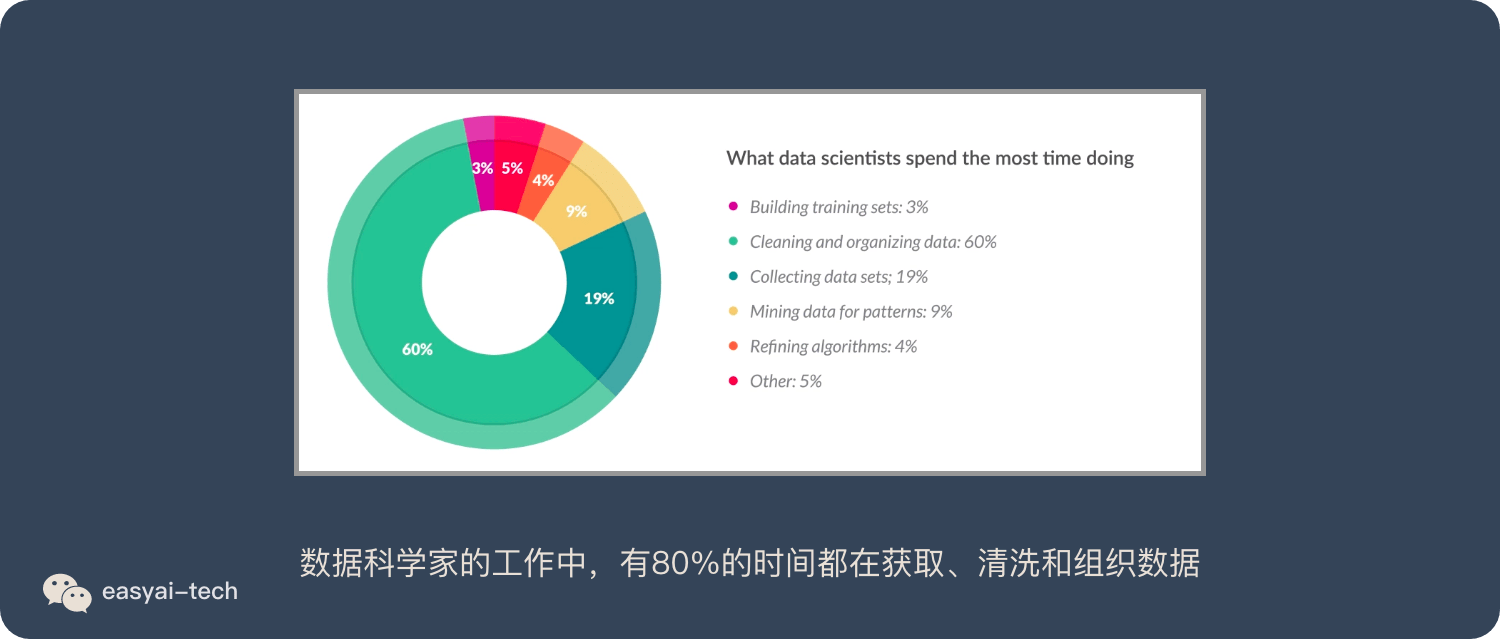
在 16 年的一项调查中发现，数据科学家的工作中，有 80%的时间都在获取、清洗和组织数据。构造机器学习流水线的时间不到 20%。详情如下：

更多内容可参考 👉这里

Q：为了避免 Overfitting，是调参好还是不调好？

�‍*♂️**：在实际应用中，对于调参没有竞赛时那么重要，因为实际生产环境中，更关心模型的 Robotics，而竞赛更关注精度，所以实际中为了达到高泛化性，适当降低精度的要求是允许的，一般大概调调参就可以，过度调参很容易导致过拟合。可以联系第一个问题，机器学习首先拼的是数据（收集、清洗、组织等待），最后拼的才是模型（模型的选择、超参数的设置、初始化方法等待）。

Q：能不能训练一个模型来预测股市、数字货币等的价格走势？

�‍♂️：目前来说以普通人的资源很难做到（可能有些量化交易公司可以做到部分的预测性），因为首先这个市场影响价格的相关信息源非常多，除了__客观事件_外，还有人类的__主观想法和信念*_。要构建一个能迅速处理多信息源、情绪检测的在线模型，首先对实时数据的收集、处理噪声就是一件非常难、成本很高的事（因为讲究时效性），同时模型的硬件构建、训练也是一个成本很高的事，以目前的方法来说，就算理论上可行，但实际的成本很可能大于模型带来的收益。