【洛谷】枚举专题-二进制枚举 从子集到矩阵问题，经典应用与实现

---

⼆进制枚举：⽤⼀个数⼆进制表⽰中的 0/1 表⽰两种状态，从⽽达到枚举各种情况。

• 利⽤⼆进制枚举时，会⽤到⼀些位运算的知识。
• 关于⽤⼆进制中的 0/1 表⽰状态这种⽅法，会在动态规划章节中的状态压缩 dp 中使⽤到。
• ⼆进制枚举的⽅式也可以⽤递归实现，后面介绍递归时再细讲。

子集

题目描述

题目解析

这道题很简单，就是一道练手题，主要重点还是在代码实现上。

代码

class Solution {
public:vector<vector<int>> subsets(vector<int>& nums) {vector<vector<int>> ret;int n = nums.size();// 枚举所有状态：000、001、010...for(int st = 0; st < (1 << n); st++){vector<int> tmp;//判断st哪些位为1，把为1的位作为nums的下标把对应的元素插入tmp中//因为与顺序无关，若要严格对应的话应该是nums[n - 1 - j]for (int j = 0; j < n; j++){if((st >> j) & 1){tmp.push_back(nums[j]);}}ret.push_back(tmp);}return ret;}
};

费解的开关

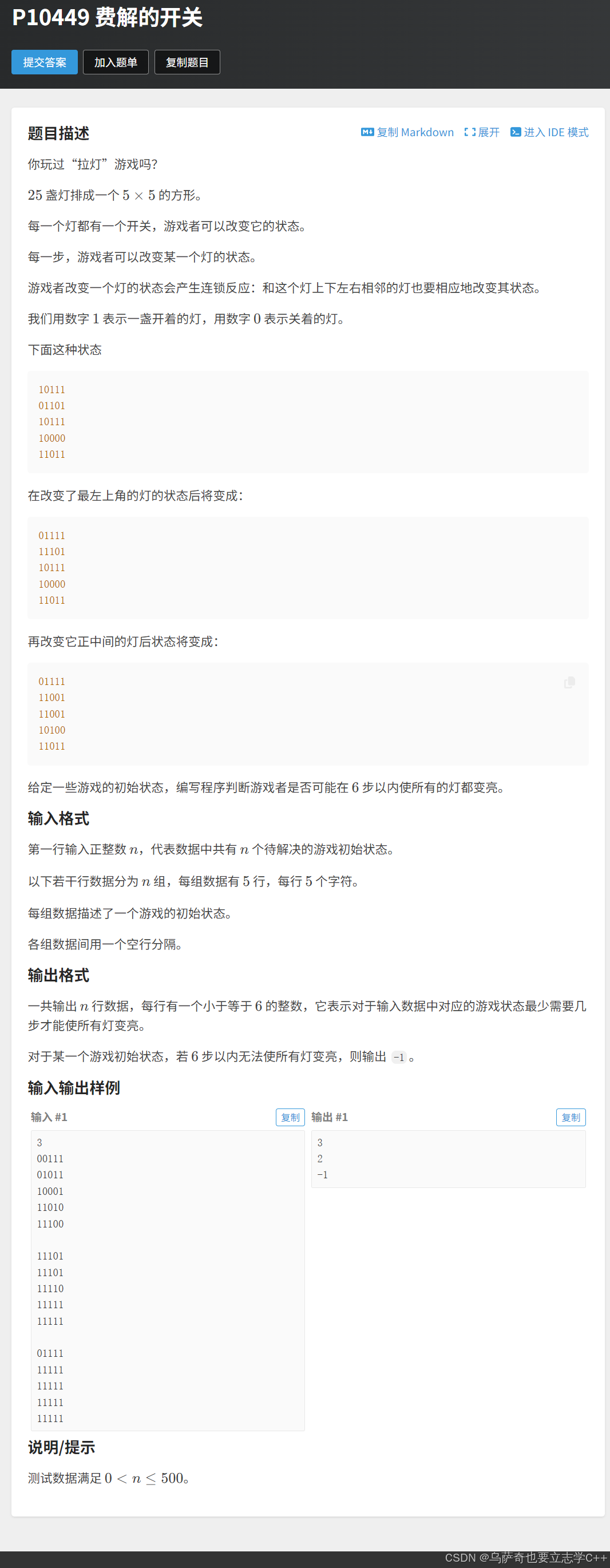
题目描述

题目解析

这道题应该是迄今为止我们遇到的最难的一题，虽然复杂，但我们把它拆分成一个一个的小点再串起来就很好理解了。

首先我们分析一下本题有哪些性质：
1、每一盏灯最多只会按一次，因为按两次后就复原了。
2、按灯后的结果与顺序无关，只与如何按有关。
3、类比之前扫雷那道题，当第一行的按法确定后，下面行的按法就跟着确定了。

本题的实现思路如下：
1、枚举第一行所有按法。
2、根据当前行的按法，计算出按后的该行状态和下一行状态。
3、根据按后的该行的状态，推导出下一行的按法，重复2、3步。
4、直到按完最后一行，判断所有灯是否全亮。

具体实现步骤：
1、把输入数据存起来，用整数的二进制形式把每行的二进制数存起来是最方便的，如二进制10000 就用16存储，然后把五行整数存入到一个数组中。而题目中的每个二进制数都是以字符的形式的存储的，所以我们要依次读入一行中的所有字符，当读到 ‘1’ 时需要a[i]的对应位置1。（小编这里用正向存储灯的亮灭（1开，0灭），但其实反向存储代码实现更简单，但是方便大家理解，还是采用正向存储）
（补充：这里正向存储虽然二进制00111会被存为整数28，但是只要后续列位操作一致，就不会影响最终结果）
2、枚举第一行的所有按法，五位二进制数一共32种按法。需要统计每一种按法能让灯全亮的步数，最小的步数若小于等于6就是所求。
3、在进行每次按法操作前，需要把按法st和数组a用临时变量存一下，因为每一次的按法操作都会修改st和数组a。
4、按法操作内部逻辑：

1）、首先统计当次push的步数，加到cnt中。
2）、把当前行按后的结果算出来。
3）、把高位的影响去除，相当于把第六位的1置为0，若不去除影响的话下一行按法就可能超出范围。
4）、把当前行按后对下一行的影响算出来，得出下一行的结果。
5) 、求下一行的按法push，下一行需要把当前行的0全部按为1。
5、当次按法结束后判断是否把所有灯都按按亮了，判断依据是看最后一行t[N-1]是否全为1。
6、最后按题意输出结果。

代码

#include <iostream>
#include <string.h>
using namespace std;//数组元素个数，多开一些空间
const int M = 10; 
const int N = 5;
int a[M];// 统计x的二进制表示中有多少个1
int calc(int x)
{int cnt = 0;while (x){cnt++;x &= x - 1;}return cnt;
}int main()
{int T;cin >> T;while(T--){// 多组测试用例，要先清空数据memset(a, 0, sizeof(a));// 1、把五位二进制数用整数的二进制形式存储//如 10000 就存为 16for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){char ch; cin >> ch;if (ch == '1')a[i] |= 1 << j;}}// 所有按法中的能让灯全亮的最小步数int ret = 0x3f3f3f3f; //算法题中安全的最大值// 1、枚举第一行所有按法（00000，00001，00010...）// 1按，0不按for (int st = 0; st < 1 << N; st++){int cnt = 0; // 该次按法的步数//下面会改变a[i]和st的值，所以需要用临时变量暂存一下int t[M];memcpy(t, a, sizeof(a));int push = st;// 2、根据第一行所有按法推导出本行按后状态和下一行状态for (int i = 0; i < N; i++){// 统计该行push的步数，并加到cnt中cnt += calc(push); //（该步骤必须写在push = t[i];的前面）// 修改当前行为按后状态（位运算有并行性，可以批量处理当前行所有灯的翻转）t[i] = t[i] ^ push ^ (push << 1) ^ (push >> 1);// 消除高位影响,如t[0]:0001010,push:0010000// 按后t[0]:0110010,0110010 &= 0011111 = 0010010t[i] &= (1 << N) - 1;// 修改下一行为按后状态t[i + 1] ^= push;// 下一行t[i + 1]的按法,需要把t[i]的0全部变为1push = ((1 << N) - 1) ^ t[i];}if(t[N - 1] == (1 << N) - 1)ret = min(ret, cnt);}if (ret <= 6)cout << ret << endl;elsecout << -1 << endl;}return 0;
}

EvenParity

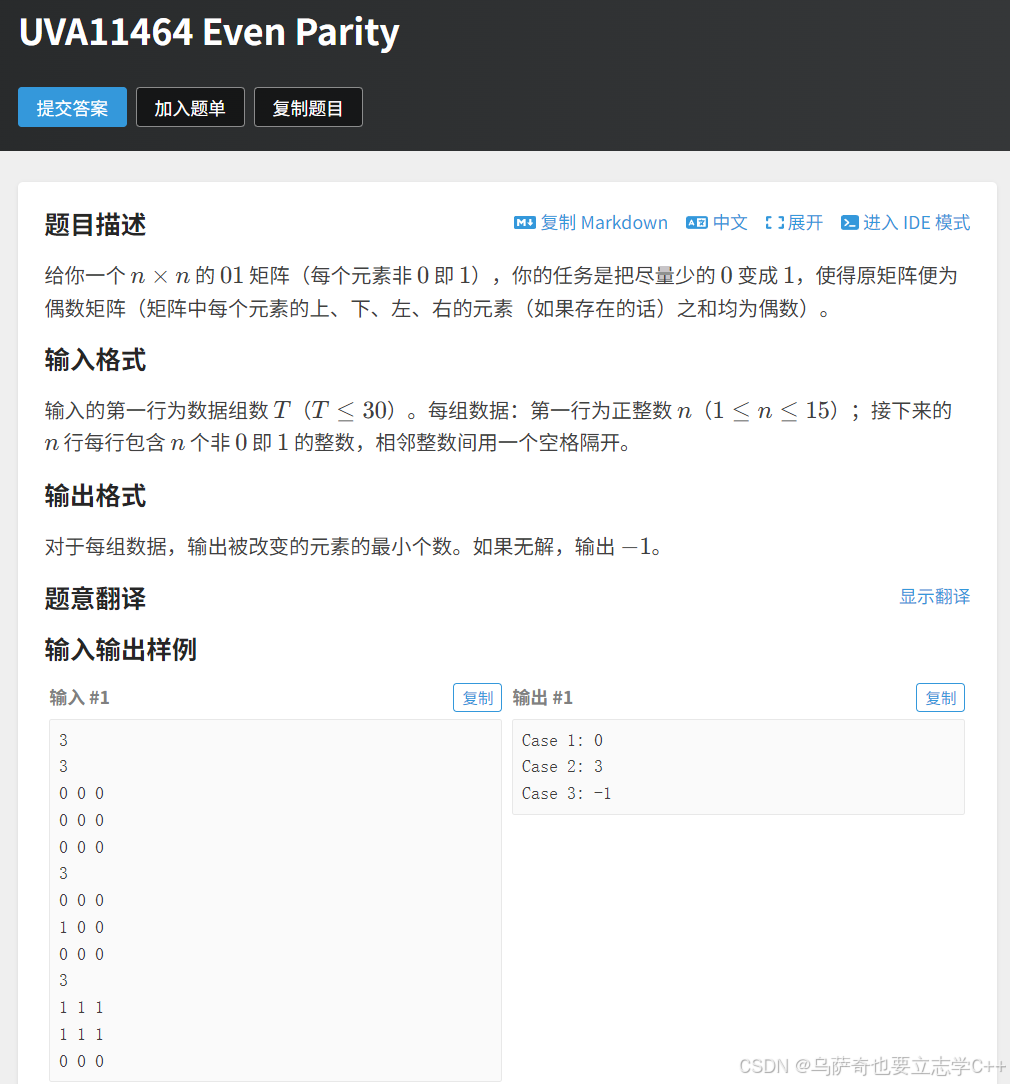
题目描述

题目解析

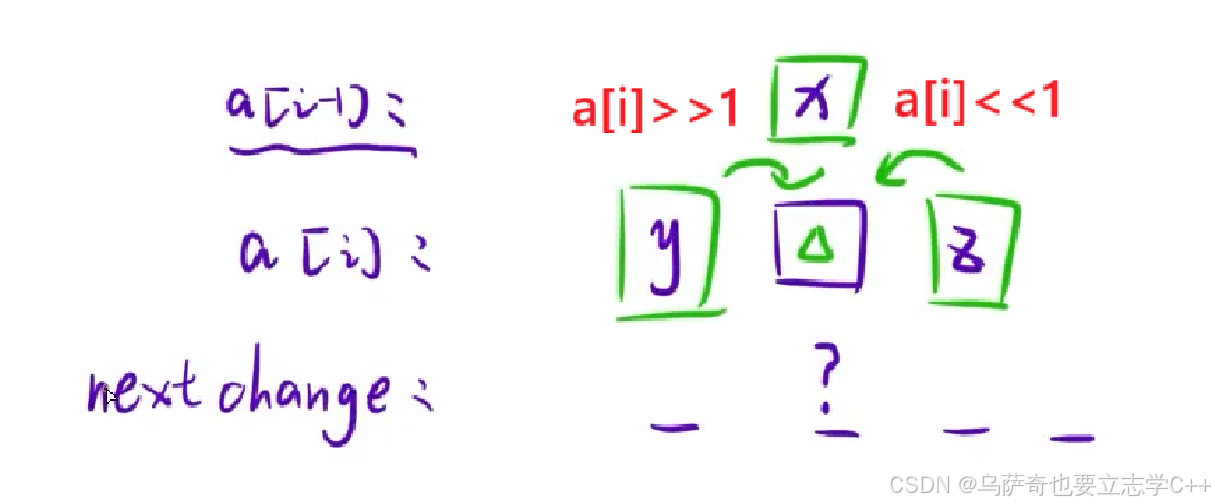
本题思路和上一题基本一致，都是依次枚举第一行所有结果，然后递推，只不过本题对于每行数据不再需要按法，而是直接推出每行的结果。并且本题需要一些位运算的特性，如下所示。

位运算特性和递推推导：
1、异或消消乐性质，一堆偶数个变量，变量只有0或1两种取值，把这堆变量全部异或起来时，若值为1的变量有偶数个，那么值为0的变量也就有偶数个，那么它们异或后的最终结果就为0。所以要让 ？取值符合题目要求 x + y + z + ？ 的结果为偶数，就需要：
x ^ y ^ z ^ ? = 0
2、我们把x ^ y ^ z 打包看成一个整体，那么要让x ^ y ^ z ^ ? = 0，就相当于：x ^ y ^ z == ?，这就是递推公式。

注意： 1、本题相比上一题，递推时会用到当前行上两行的数据，所以本题需要从数组下标1开始存储数据，避免越界访问。
2、本题也需要清除无效高位影响，因为递推公式是建立在有效数据外面一圈全是0的基础上的，若不清除无效高位影响会导致递推公式中原本应该异或右移来的0，但是实际却异或成了1导致结果出错。

代码

#include <iostream>
#include <cstring>
using namespace std;const int M = 20;int a[M];
int t[M]; //备份
int n;// 判断x->y是否合法 0->1合法  1->0非法
int calc(int x, int y)
{int cnt = 0;for (int i = 0; i < 16; i++){// 0->1合法if (((x >> i) & 1) == 0 && ((y >> i) & 1) == 1)cnt++;// 1->0不合法if (((x >> i) & 1) == 1 && ((y >> i) & 1) == 0)return -1;}return cnt;
}int solve()
{// 保存该组数据最小0->1次数int ret = 0x3f3f3f3f;// 依次枚举第一行的最终状态 for (int st = 0; st <= ((1 << n) - 1); st++){// 暂存a[i]memcpy(t, a, sizeof(a));// 记录每一次第一行枚举总的0->1次数int cnt = 0;// 默认该次合法int flag = 1;// 递推下一行的结果int change = st;// 根据第一行结果依次递推下面行 行for (int j = 1; j <= n; j++){// 判断是否存在非法转换：1->0,若有返回-1，// 若没有，返回 0->1次数int c = calc(a[j], change);if (c == -1){flag = 0;break;}// 把该行0->1次数加到cnt中cnt += c;// 当前行的最终状态t[j] = change;// 按递推公式推导下一行最终状态change = t[j - 1] ^ (t[j] << 1) ^ (t[j] >> 1);// 消除无效高位影响,若不清除无效高位会存到change中// change为下一行目标状态，不清除影响下一行change &= ((1 << n) - 1);}if (flag){ret = min(cnt, ret);}}if (ret == 0x3f3f3f3f){return -1;}else{return ret;}
}int main()
{int T;cin >> T;// 组for (int z = 1; z <= T; z++){// 多组数据，先清空上一组数据memset(a, 0, sizeof(a));cin >> n;for (int i = 1; i <= n; i++){for (int j = n - 1; j >= 0; j--){int ch; cin >> ch;if (ch == 1){a[i] |= (1 << j);}}}printf("Case %d: %d\n", z, solve());}return 0;
}

以上就是小编分享的全部内容了，如果觉得不错还请留下免费的赞和收藏
如果有建议欢迎通过评论区或私信留言，感谢您的大力支持。
一键三连好运连连哦~~