当前位置：首页 > news >正文

算法笔记 10

news 2025/11/6 12:46:31

二叉树系列算法核心纲领 | labuladong 的算法笔记https://labuladong.online/algo/essential-technique/binary-tree-summary/这篇笔记容量很大，干货满满，需要反复复盘，值得反复学习的重磅好文。

1 对二叉树前中后序遍历的深入解读

前序位置的代码在刚刚进入一个二叉树节点的时候执行；

后序位置的代码在将要离开一个二叉树节点的时候执行；

中序位置的代码在一个二叉树节点左子树都遍历完，即将开始遍历右子树的时候执行。
前中后序的本质前中后序并非仅仅是三个元素顺序不同的列表，而是遍历二叉树时处理节点的三个特殊 “时间点”：
- 前序位置：刚进入节点时执行代码。
- 中序位置：遍历完左子树、即将遍历右子树时执行代码。
- 后序位置：将要离开节点时执行代码。
后序遍历的特殊性后序位置的代码执行时机是在节点的左右子树都遍历完成之后，这使得它天然适合处理子树相关的后续逻辑，比如计算子树的高度、统计子树的节点数、释放子树内存等（只有当子树的逻辑都处理完，才能对当前节点进行最终操作）。
多叉树无中序遍历的原因二叉树的中序遍历依赖于 “左子树 - 根节点 - 右子树” 的二叉结构，多叉树的节点有多个子节点，不存在 “左子树遍历完、即将遍历右子树” 这样明确且统一的中间时机，因此没有中序遍历的概念。

2 二叉树递归解法的两类思路及函数命名习惯

解法分类与对应算法框架
- 遍历思路：遍历一遍二叉树得出答案，对应回溯算法核心框架，函数签名一般为void traverse(...)，无返回值，靠更新外部变量计算结果。
- 分解问题思路：通过分解问题计算答案，对应动态规划核心框架，函数名依具体功能而定，一般有返回值，返回子问题的计算结果。
函数命名习惯的意义这种命名风格能突出函数作用和解题思维模式，例如回溯的void backtrack(...)无返回值，动态规划的dp函数有返回值，与二叉树两种递归思路的函数设计逻辑一致，便于理解和运用。

3 二叉树前序遍历的分解式理解

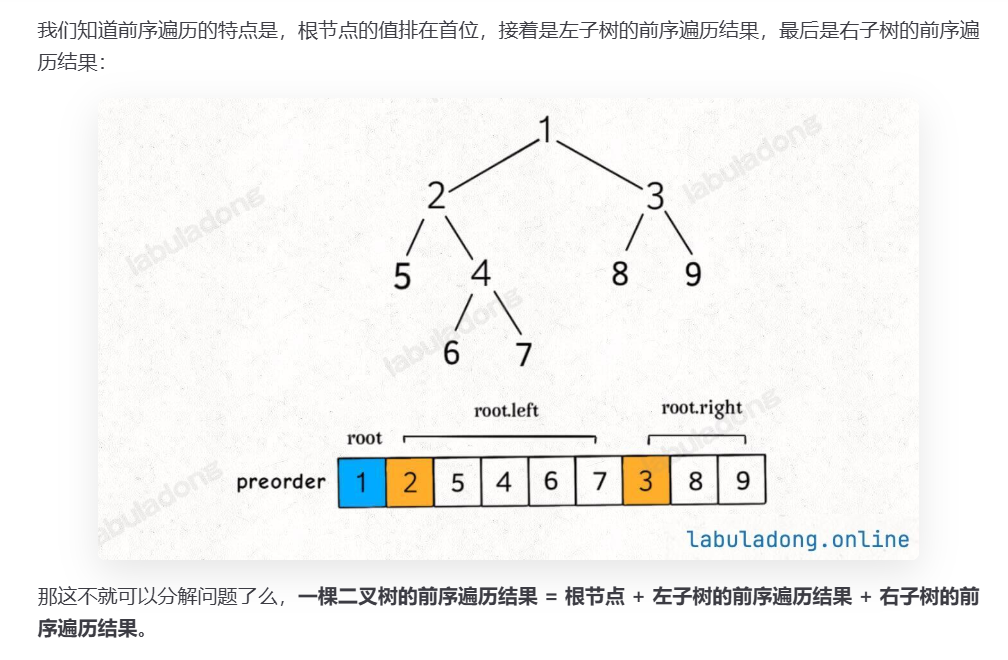
前序遍历的结构特点前序遍历结果的结构为：根节点 + 左子树的前序遍历结果 + 右子树的前序遍历结果。以图中二叉树为例，根节点是1，左子树的根是2，其前序遍历为2 5 4 6 7；右子树的根是3，其前序遍历为3 8 9，最终前序遍历序列为1 2 5 4 6 7 3 8 9，完全符合该结构。
分解问题的意义这种结构可以将二叉树的前序遍历问题分解为 “根节点处理 + 左子树遍历 + 右子树遍历” 三个子问题，体现了递归分解问题的思路，也为理解二叉树的构造、遍历类算法提供了基础逻辑。

class Solution {
public:// 定义：输入一棵二叉树的根节点，返回这棵树的前序遍历结果vector<int> preorderTraversal(TreeNode* root) {vector<int> res;if (root == nullptr) {return res;}// 前序遍历的结果，root->val 在第一个res.push_back(root->val);// 利用函数定义，后面接着左子树的前序遍历结果vector<int> left = preorderTraversal(root->left);res.insert(res.end(), left.begin(), left.end());// 利用函数定义，最后接着右子树的前序遍历结果vector<int> right = preorderTraversal(root->right);res.insert(res.end(), right.begin(), right.end());return res;}
};

insert的写法

在 C++ 中，insert 是容器（如 vector、list、string 等）的成员函数，用于在容器的指定位置插入元素或元素范围。

以你代码中的 vector<int> 为例，res.insert(res.end(), left.begin(), left.end()) 的作用是：将 left 容器中从 begin() 到 end() 的所有元素，插入到 res 容器的 end() 位置（即容器末尾），从而实现将左子树的前序遍历结果拼接在根节点之后。

简单来说，insert 在这里的功能是批量插入元素，实现多个容器间的内容拼接，帮助我们构建出 “根节点 + 左子树前序 + 右子树前序” 的完整前序遍历序列。

4 前中后序代码的能力

BST 是二叉搜索树（Binary Search Tree）的简称，也叫二叉排序树，是一种特殊的二叉树，具有以下核心特性：

节点值约束：若左子树非空，左子树上所有节点的值均小于根节点的值；若右子树非空，右子树上所有节点的值均大于根节点的值；左右子树也分别是二叉搜索树。
中序遍历有序性：对 BST 进行中序遍历，会得到一个递增的有序序列，这一特性使其在需要有序数据的场景中非常实用，比如可将其视为 “遍历有序数组”。
高效操作：基于其结构特性，BST 的查找、插入、删除操作在理想情况下时间复杂度为 O (log n)，适合动态数据的管理场景，是很多高级数据结构（如 AVL 树、红黑树）的基础。