当前位置：首页 > news >正文

GJOI 10.28 题解

news 2025/11/6 18:06:46

1.AT_abc200_e Patisserie ABC 2

题意

在这里插入图片描述

思路

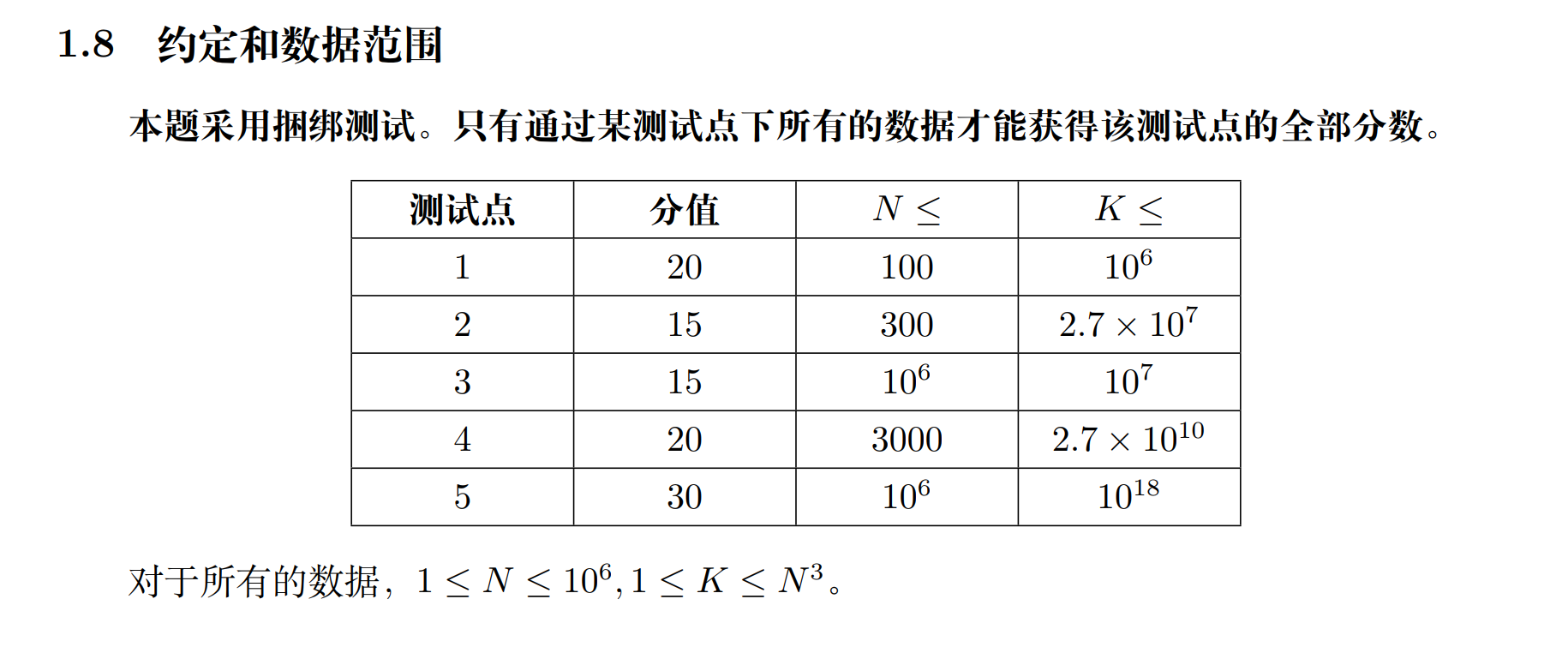
问题转化为，用 $3$ 个数组成和为 $s$ ，要求每个数 $≤n\le n$ ，求方案数。

这个问题可以容斥。首先容易用插板法算出没有限制的组合有 $(s−12)\binom{s-1}{2}$ ，之所以会多出情况是因为有的三元组中出现了 $> n$ 的数。对于这类超限限制可以直接计算 $s - n$ 的和的方案数，然后随便 $3$ 个数中选一个 $+ n$ 使其超限，就能还原出超限的三元组。即 $−(31)(s−n−12)-\binom{3}{1}\binom{s-n-1}{2}$ ，钦定 $1$ 个数大于 $> n$ 的方案数。

但是又出现了一个问题：对于一个有两个超限的三元组，显然有 $2$ 种和为 $s - n$ 的三元组可以把它还原，就减多了。例如 $s = 9, n = 3$ ， $(4, 1, 4)$ 的情况可以由和为 $6$ 的 $(1, 1, 4)$ 和 $(4, 1, 1)$ 还原回去。于是根据容斥原理，减去钦定 $2$ 个数 $> n$ 的方案数： $+(32)(s−2n−12)+\binom{3}{2}\binom{s-2n-1}{2}$ 。

显然不可能有 $3$ 个数同时超限。

ll cal(ll s)
{return Cx2(s-1)-3*Cx2(s-n-1)+3*Cx2(s-2*n-1);//C(s-1,2)-C(3,1)*C(s-n-1,2)+C(3,2)*C(s-2*n-1)
}

然后根据题意模拟排名即可。

代码1

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll n,k;
ll Cx2(ll x)
{if(x<=1)return 0;return x*(x-1)/2;
}
ll cal(ll s)
{return Cx2(s-1)-3*Cx2(s-n-1)+3*Cx2(s-2*n-1);//C(s-1,2)-C(3,1)*C(s-n-1,2)+C(3,2)*C(s-2*n-1)
}
int main()
{freopen("spaceship.in","r",stdin);freopen("spaceship.out","w",stdout);scanf("%lld%lld",&n,&k);for(ll s=3;s<=3*n;s++){ll cnt=cal(s);if(k>cnt){k-=cnt;continue;}for(ll a=1;a<=n;a++){ll s2=s-a;if(s2>n*2)continue;ll b=max(1ll,s2-n),c=s2-b;if(k>c-b+1)k-=c-b+1;else {while(1){if(k==1){printf("%lld %lld %lld",a,b,s-a-b);return 0;}b++;k--;}}}}if(k==0)printf("%lld %lld %lld",n,n,n);return 0;
}

也可以先处理两个数的，设 $g_s$ 表示两个 $≤n\le n$ 的数组成和为 $s$ 的方案数，这个搞个上下界就能预处理。设 $f_s$ 表示三个 $≤n\le n$ 的数组成和为 $s$ 的方案数，枚举第三个数 $i$ 然后合并 $g_{s-i}$ ，但是这个要 $O(n^2)$ ，所以直接预处理 $i$ 的上下界然后取 $g$ 的前缀和优化即可。具体可以看这篇博客。

2.P7150 Stuck in a Rut S

题意

在这里插入图片描述

思路

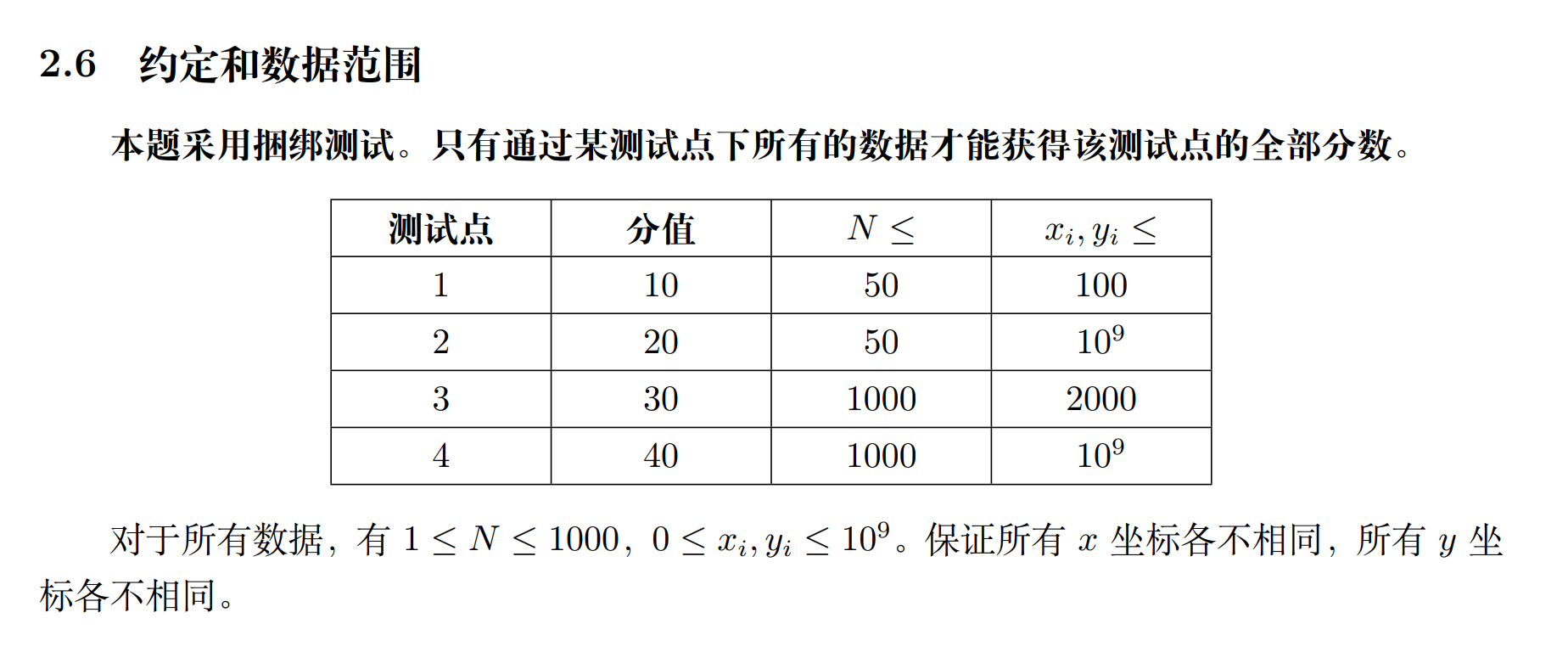
把机器人分成 E 和 N 两组，因为同方向的必然不会撞到一起。分别枚举两组各自的机器人 $i, j$ ，必然有其中一个机器人存活时间遭到限制。

写出一个四元组 $(s h, b s, w 1, w 2)$ 表示 $s h$ 杀死 $b s$ ， $s h$ 需要 $w 1$ 步，而 $b s$ 还能存活 $w 2$ 。贪心地按照存活时间排序，维护每个点的存活时间，即能画出干与被干的 DAG，DAG 上计数即可。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=1009,inf=0x3f3f3f3f;
ll n;
struct point
{ll x,y,id;
}nor[N],eas[N];
ll tn,te,tot;
struct term
{ll sha,bs,w1,w2;
}b[N*N];
bool cmp(term x,term y)
{if(x.w2!=y.w2)return x.w2<y.w2;return x.w1<y.w1;
}
ll dis[N];
vector<ll>G1[N];
ll f[N],out[N];
void topo()
{queue<ll>q;for(int i=1;i<=n;i++)if(!out[i])q.push(i);while(!q.empty()){ll u=q.front();q.pop();for(auto v:G1[u]){f[v]+=f[u]+1;out[v]--;if(!out[v])q.push(v);}}
}
int main()
{freopen("robot.in","r",stdin);freopen("robot.out","w",stdout);scanf("%lld",&n);for(int i=1;i<=n;i++){char op;ll x,y;cin>>op;scanf("%lld%lld",&x,&y);if(op=='N')nor[++tn]=(point){x,y,i};else eas[++te]=(point){x,y,i};}for(int i=1;i<=te;i++){for(int j=1;j<=tn;j++){if(eas[i].x<=nor[j].x&&eas[i].y>=nor[j].y){ll w1=nor[j].x-eas[i].x;//东沙 ll w2=eas[i].y-nor[j].y;//北沙 if(w1==w2)continue;if(w1<w2)b[++tot]=(term){eas[i].id,nor[j].id,w1,w2};else b[++tot]=(term){nor[j].id,eas[i].id,w2,w1};}}}sort(b+1,b+tot+1,cmp);memset(dis,inf,sizeof(dis));for(int i=1;i<=tot;i++){if(dis[b[i].sha]>=b[i].w1&&dis[b[i].bs]>=b[i].w2){dis[b[i].bs]=min(dis[b[i].bs],b[i].w2);G1[b[i].bs].push_back(b[i].sha);out[b[i].sha]++;}}topo();for(int i=1;i<=n;i++)printf("%lld\n",f[i]);return 0;
}

3.洛谷 P8162 JOI2022 Final 让我们赢得选举 / Let’s Win the Election

题意

在这里插入图片描述

思路

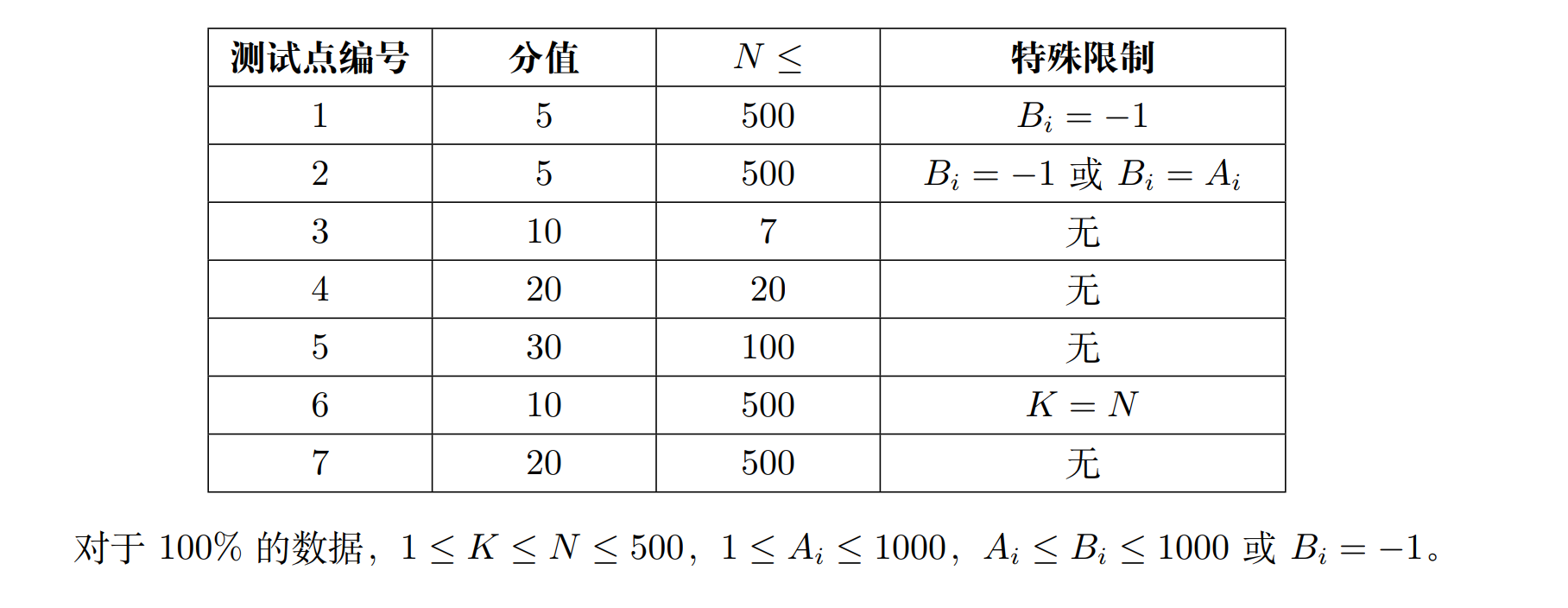
对于协作者肯定是在 $b$ 小的选走，于是按照 $b$ 从小到大排序。想用两点贪心：

先在要获得协作者的州演讲，把所有州的协作者拉拢后，再去其他的；
自己和所有协作者一起拼一个州，因为 $min⁡i=1n{x1y1,x2y2,...,xnyn}≤∑i=1nxi∑i=1nyi≤max⁡{x1y1,x2y2,...,xnyn}\min_{i=1}^n\{\frac{x_1}{y_1},\frac{x_2}{y_2},...,\frac{x_n}{y_n}\}\le \frac{\sum_{i=1}^nx_i}{\sum_{i=1}^ny_i}\le \max\{\frac{x_1}{y_1},\frac{x_2}{y_2},...,\frac{x_n}{y_n}\}$ ；

钦定要选到 $x$ 个协作者，按理来说是在前面 $i$ 个从头开选， $i$ 个里选连续 $x$ 个。但是要预料到前 $i$ 个中，中间挖掉一个不选会更优的情况（一种可能的，搞定 $a_i$ 比较小，但是 $b_i$ 相对较大，从而劣）。于是要考虑 dp。

按照 $b$ 从小到大排序，钦定前 $x$ 个可以选协作者，设 $f_{i,j}$ 表示，前 $i$ 个州拉拢到 $j$ 个协作者的最少时间。然后转移，不选：
$fi,j←fi−1,j+ai÷(x+1)f_{i,j}\leftarrow f_{i-1,j}+a_i\div(x+1)$

这里是 $÷(x+1)\div (x+1)$ ，是因为根据上面的贪心，拉拢完所有协作者之后再去一起做只用拿选票的，所以此时已经拉拢了 $x + 1$ 个协作者了，而不是 $÷(j+1)\div(j+1)$ 。

然后选：
$fi,j←fi−1,j−1+bi÷jf_{i,j}\leftarrow f_{i-1,j-1}+b_i\div j$

因为按顺序来到 $i$ ，演讲 $b_i$ 拿到协作者，前面只有 $j - 1$ 个协作者，加上自己就 $÷j\div j$ 。在 $1∼i1\sim i$ 选出了 $x$ 个协作者后，就可以去后面的城市演讲，直到凑够 $k$ 。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define dd double
const ll N=506,inf=2e9;
ll n,k;
struct node
{dd a,b;
}p[N];
bool cmp(node x,node y)
{return x.b<y.b;
}
dd f[N][N],ans=inf;
dd aa[N];
int main()
{freopen("election.in","r",stdin);freopen("election.out","w",stdout); scanf("%lld%lld",&n,&k);for(int i=1;i<=n;i++){dd a,b;scanf("%lf%lf",&a,&b);if(b==-1)b=inf;p[i]=(node){a,b};}sort(p+1,p+n+1,cmp);for(int x=0;x<=k;x++){for(int i=1;i<=n;i++)aa[i]=p[i].a;for(int i=0;i<=n;i++)for(int j=0;j<=n;j++)f[i][j]=inf;f[0][0]=0;for(int i=1;i<=n;i++){for(int j=0;j<=min(i,x);j++){f[i][j]=f[i-1][j]+p[i].a/(dd)(x+1);if(j&&p[i].b!=inf)f[i][j]=min(f[i][j],f[i-1][j-1]+p[i].b/(dd)j);}}dd ret=inf;for(int i=k;i<=n;i++)ret=min(ret,f[i][x]);for(int i=k;i>=x;i--){dd s=0;sort(aa+i+1,aa+n+1);for(int j=i+1;j<=k;j++)s+=aa[j];ret=min(ret,f[i][x]+s/(dd)(x+1));}ans=min(ans,ret);}printf("%.15lf",ans);return 0;
}