当前位置：首页 > news >正文

拓扑排序的实现

news 2025/11/6 10:33:56

在前面几期，我们给大家介绍了几种求最短路径的算法以及用代码的具体实现，今天我们给大家介绍一种关于图的排序算法-----拓扑排序

拓扑排序:在图论中，由一个有向无环图的顶点组成的序列，当且仅当满足下列条件式，称为该图的一个拓扑排序:

1.每个顶点出现且出现一次

2.若顶点A在序列中排在B的前面，则在图中不存在从顶点B到顶点A的路径。

总结来说拓扑排序就是找到做事情的先后循序

如图:

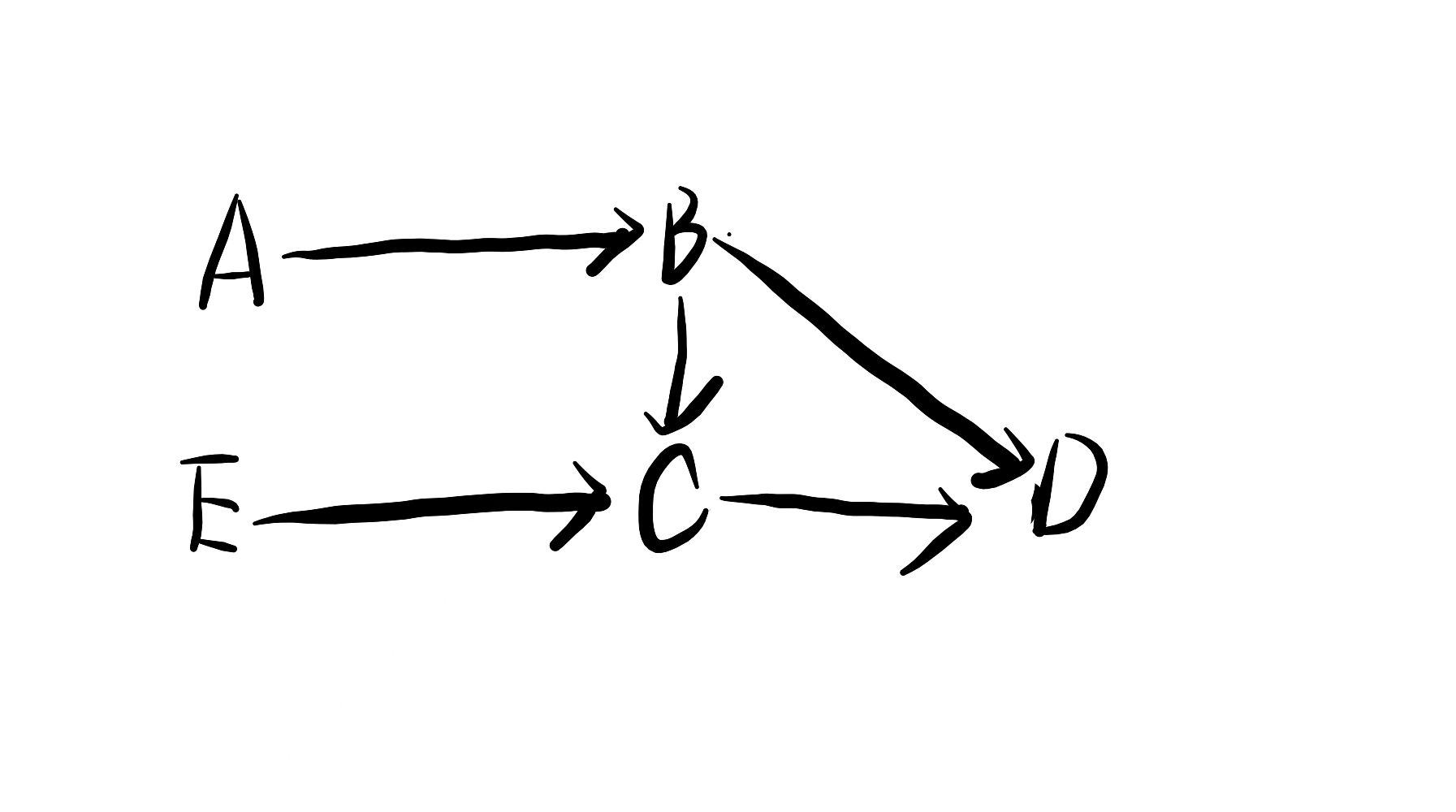
邻接表为:

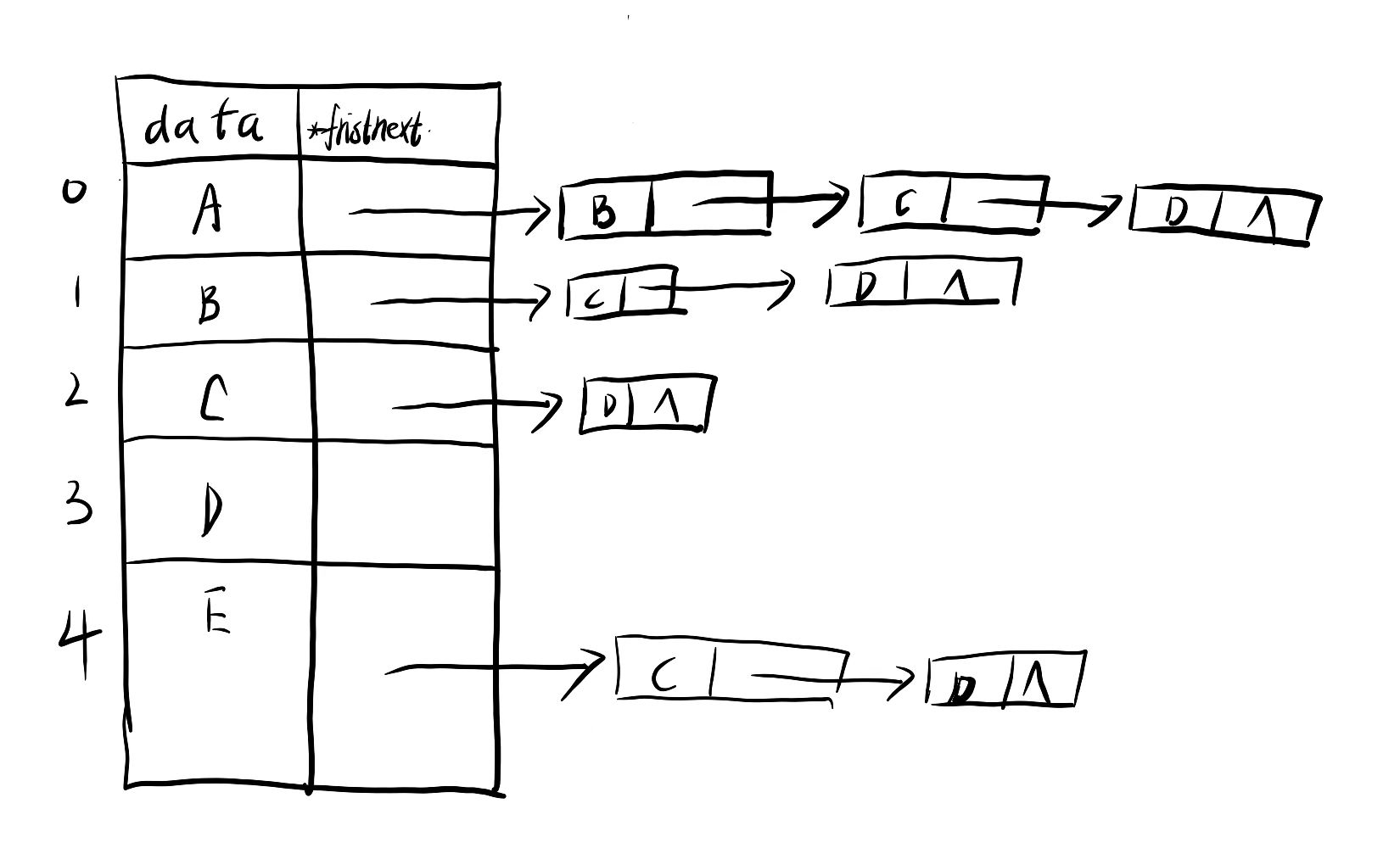
实现拓扑排序的具体思想:

1.AOV网中选择一个没有前驱(入度为0)的顶点并输出

2.从网中删除该顶点和所有以它为起点的有向边

3.重复1和2直到当前的AOV网为空或当前网中不存在无前驱的顶点为止

代码实现:

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdbool.h>
#include<stdlib.h>
#include<limits.h>
#define VertexNum 5
//定义边
typedef struct Edge
{
int adjvex;//邻接顶点的索引
struct Edge* next;//下一个顶点的位置
}Edge;
//定义顶点
typedef struct VNode
{
char data;//顶点
struct Edge* first;//指向该顶点第一条边
}VNode;
//定义图
typedef struct array
{
VNode arr[VertexNum];//定义数组
int Vertex;//顶点和边的数量
}Graph;
//这样的话就是存在一个arr数组，数组里的每个元素都是VNode型的，每个元素里面有个顶点和顶点的第一条边的指针
//每一个指针里面又有下一个顶点在数组里的下标和地址
typedef struct SNode
{
int data;//数据域
struct SNode* next;//下一个结点
}SNode,*LinkStack;

//初始化图
void InitGraph(Graph* G)
{
//给每个数据域赋为0，指针域赋为空
int i = 0;
for (i; i < VertexNum; i++)
{
G->arr[i].data = '\0';
G->arr[i].first = NULL;
}
G->Vertex = 0;
}
//插入顶点
bool EnVertex(Graph* G)
{
if (G->Vertex >= VertexNum)//如果顶点的数量大于等于数组的长度
return false;
int i;
for (i = 0; i < VertexNum; i++)
{
G->arr[i].data = 'A' + i;
}
//顶点数量
G->Vertex = VertexNum;
return true;
}
//将无向邻接表改为有向邻接表
//插入边
bool EnEdge(Graph* G)
{
if (G->Vertex <= 1)
return false;//1个顶点无需边
//为每个顶点的邻接顶点创建指针
//int i;

   //A顶点
G->arr[0].first = (Edge*)malloc(sizeof(Edge));
if (G->arr[0].first == NULL)
return false;
Edge* p = G->arr[0].first;
p->adjvex = 1;
p->next = NULL;
//for (i = 2; i <= 3; i++)
//{
//   Edge* s = (Edge*)malloc(sizeof(Edge));
//   if (s == NULL)
//       return false;
//   s->adjvex = i;
//   s->next = NULL;
//   p->next = s;
//   p = s;
//}

//B顶点
G->arr[1].first = (Edge*)malloc(sizeof(Edge));
if (G->arr[1].first == NULL)
return false;
Edge* q = G->arr[1].first;
q->adjvex = 2;
q->next = (Edge*)malloc(sizeof(Edge));
if (q->next == NULL)
return false;
q = q->next;
q->adjvex = 3;//指向D
q->next = NULL;

//C顶点
G->arr[2].first = (Edge*)malloc(sizeof(Edge));
if (G->arr[2].first == NULL)
return false;
Edge* C1 = G->arr[2].first;
C1->adjvex = 3;
C1->next = NULL;

   //D顶点
//G->arr[3].first = (Edge*)malloc(sizeof(Edge));
//if (G->arr[3].first == NULL)
//   return false;
//Edge* D1 = G->arr[3].first;
////D的邻接顶点A
//D1->adjvex = 0;
////D的邻接顶点B
//D1->next = (Edge*)malloc(sizeof(Edge));
//if (D1->next == NULL)
//   return false;//分配失败
//D1 = D1->next;
//D1->adjvex = 1;
//D1->next = (Edge*)malloc(sizeof(Edge));
//if (D1->next == NULL)
//   return false;//分配失败
//D1 = D1->next;
//D1->adjvex = 4;
//D1->next = NULL;

//E顶点
G->arr[4].first = (Edge*)malloc(sizeof(Edge));
if (G->arr[4].first == NULL)
return false;
Edge* E1 = G->arr[4].first;
//E的邻接顶点C
E1->adjvex = 2;
E1->next = NULL;

return true;
}
//拓扑排序
//初始化栈
int degree[VertexNum];//表示顶点的入度
int print[VertexNum];//表示顶点的出栈序列
void InitStack(LinkStack* S)
{
(*S) = NULL;
}
//进栈
bool Push(LinkStack* S,int i)
{
//链式队列无需判断满栈
//创建结点
SNode* p = (SNode*)malloc(sizeof(SNode));
if (p == NULL)
return false;
p->data = i;
p->next = (*S);
(*S) = p;
return true;
}
//判断栈不为空
bool EmptyStack(LinkStack* S)
{
if ((*S) == NULL)
return true;
return false;
}
//出栈
int Pop(LinkStack* S)
{
if ((*S) == NULL)
return INT_MAX;//空栈
int dingdian;
SNode* top = (*S);//栈顶指针
(*S) = (*S)->next;//更新栈顶指针
dingdian = top->data ;//保留栈顶数据
free(top);//释放内存空间
return dingdian;
}
//求图G中顶点x的第一个邻接点，若有则返回顶点号。若x没有邻接点或图中不存在x，则返回 -1
int FirstNeighbor(Graph G, char x)
{
if (G.Vertex == 0)
return -1;//非法图
if (G.Vertex == 1)
return -1;//只有一个顶点
int i;
int index = -1;
//求顶点的下标
for (i = 0; i < VertexNum; i++)
if (G.arr[i].data == x)
index = i;
if (index == -1)
return -1;//不存在顶点
//返回邻接顶点号
return G.arr[index].first->adjvex;
}
//假设图G中顶点y是顶点x的一个邻接点，返回除y之外顶点x的下一个邻接点的顶点号，若y是x的最后一个邻接点，则返回 - 1
int NextNeighBor(Graph G,char x,char y)
{
if (G.Vertex == 0)
return -1;//非法图
if (G.Vertex == 1)
return -1;//图中只有一个顶点
//求当前顶点的下标
int index = -1;
int i;
for (i = 0; i < VertexNum; i++)
if (G.arr[i].data == x)
{
index = i;
break;
}
if (index == -1)
return -1;//不存在该顶点
Edge* p = G.arr[index].first;

while (p != NULL)
{
if (G.arr[p->adjvex].data == y)//找到了y
return p->next->adjvex;
else//没有找到y
return -1;
}

return -1;
}
//拓扑排序
bool TopologicalSort(Graph G,LinkStack* S)
{
if (G.Vertex == 0)
return false;//非法图
if (G.Vertex == 1)
return false;//只有一个顶点
//初始化栈
InitStack(S);
//初始化数组
int i;
for (i = 0; i < VertexNum; i++)//print[]数组
print[i] = -1;
//degree数组
degree[0] = 0;
degree[1] = 1;
degree[2] = 2;
degree[3] = 2;
degree[4] = 0;

//进行拓扑排序
//令入度为0的顶点入栈
for (i = 0; i < VertexNum; i++)
{
if (degree[i] == 0)
Push(S,i);
}
int count = 0;//记录顶点的数量
int dingdian = -1;
while (EmptyStack(S) == false) //判断栈不为空的情况
{
dingdian = Pop(S);
if(dingdian >= 0 && dingdian < VertexNum)
print[count] =dingdian ;//打印出栈的顶点
count++;
//将dingdian指向的顶点入度-1，并且将为0的顶点入栈
Edge* p = G.arr[dingdian].first;
while(p != NULL)
{
int index = p->adjvex;
degree[index]--;
//如果此时入度为0则直接进栈
if (degree[index] == 0)
Push(S, index);
p = p->next;
}
}
if (count < VertexNum)
return false; //排序失败
return true;//排序成功
}
void Print(int print[])
{
int i;
for (i = 0; i < VertexNum; i++)
{
printf("%d ", print[i]);
}
printf("\n");
}