当前位置：首页 > news >正文

神经网络常见操作

news 2025/11/6 8:50:44

卷积

dim=d的tensor可以进行torch.nn.Convnd(in_channels,out_channels),其中n=d-1,d-2
对于torch.nn.Convnd(in_channels,out_channels)，改变的是tensor的倒数n+1维的大小

n维卷积指的是卷积核的空间形状是n维的，也就是滑动方向是n维的，但是在PyTorch中核张量的维度不是n维的。

无论是一维、二维还是三维卷积，每个卷积核都会作用于所有输入通道,输出通道数都等于卷积核的个数。

下面是一个多通道的二维卷积图示，一共有一个卷积核，这个卷积核作用于所有的通道，也就是作用于三个通道，因为只有一个卷积核，所以生成一个特征图
以下我们将333的卷积核称为完整卷积核，将其按通道分成3份后，每一份称为子核
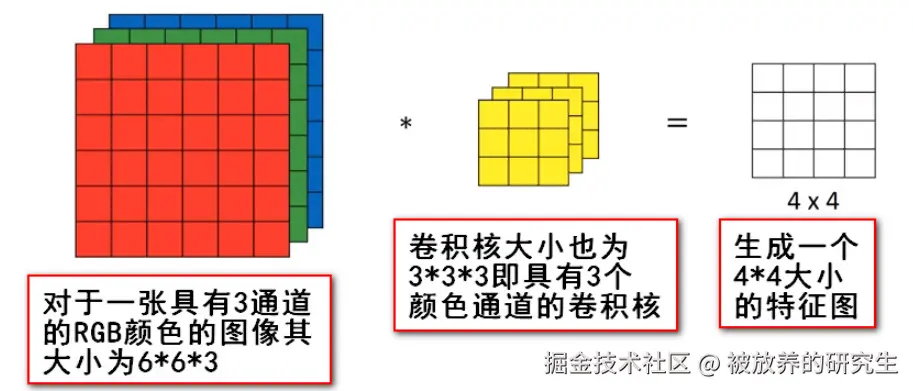
在这里插入图片描述
带入公式算一下，卷积核张量维度4D(1,3,3,3)
卷积核的完整张量维度需要同时描述「通道维度」和「空间维度」，不同维度的卷积，通道维度都是（out_channels, in_channels//groups），区别只在空间维度。

维度	一维卷积（`nn.Conv1d`）	二维卷积（`nn.Conv2d`）	三维卷积（`nn.Conv3d`）
滑动方向	1个（长度）	2个（高度、宽度）	3个（深度/时间、高度、宽度）
卷积核空间形状	1D（`kernel_size`）	2D（`kernel_height, width`）	3D（`kernel_depth, height, width`）
核张量维度	3D（`out_channels, in_channels//groups, kernel_size`）	4D（`out_channels, in_channels//groups, kernel_h, kernel_w`）	5D（`out_channels, in_channels//groups, kernel_depth,kernel_h, kernel_w`）

nn.Convnd(in_channels,out_channels,kernel_size,stride,padding,dilation,groups,bias,padding_mode)

输入: $N, C_{in}, D, H, W)$
输出: $N, C_{out}, D_{out}, H_{out}, W_{out})$
math: $out(Ni,Coutj)=bias(Coutj)+∑k=0Cin−1weight(Coutj,k)⋆input(Ni,k)\text{out}(N_i, C_{\text{out}_j}) = \text{bias}(C_{\text{out}_j}) +\sum_{k = 0}^{C_{in} - 1} \text{weight}(C_{\text{out}_j}, k) \star \text{input}(N_i, k)$
k是指第k个通道
卷积核的通道数等于输入的通道数
一个样本对应一个或多个通道，一个通道对应一个子核
一个完整卷积核对应一个卷积操作，卷积操作的结果是生成一个整体的张量

全连接

nn.Linear(in_features: int, out_features: int, bias: bool = True)

math: $y = xA^T + b$
The shape of x is [batch_size, in_features]
The shape of A^T is [in_features,out_features].
The shape of b is [out_features].

激活函数

nn.ReLU(inplace: bool = False)

math: $x≤0\text{ReLU}(x) = \begin{cases} x, & \text{if } x > 0 \\ 0, & \text{if } x \leq 0 \end{cases}$

nn.Sigmoid()

math: $Sigmoid(x)=σ(x)=11+exp⁡(−x)\text{Sigmoid}(x) = \sigma(x) = \frac{1}{1 + \exp(-x)}$

归一化

LayerNorm

class torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True, bias=True, device=None, dtype=None)
核心逻辑是对 “单个样本” 的指定维度计算统计量（均值 / 方差） ，不依赖批次内其他样本
对于一个形状为（N,C，H,W）的张量，选样本内的”最后连续k个维度"，k<=3,无批次依赖

BatchNorm2d

核心逻辑是对 “整个批次（N 个样本）” 的 “单个通道” 计算统计量，即每个通道的统计量由该批次所有样本在该通道的所有空间像素共同决定，因此归一化维度严格绑定 N 维度（批次） 和 空间维度（H、W） ，仅对 C 维度（通道） 独立处理。
对于一个形状为（N,C，H,W）的张量,是对对每个通道 c，将该通道的 N×H×W 个元素归一化

GroupNorm

GroupNorm 是 BatchNorm 的改进，核心逻辑是对 “单个样本” 的 “通道分组” 计算统计量—— 先将 C 个通道分成 G 个组（每组 C/G 个通道），再对每个组内的 “所有空间像素（H×W）” 计算统计量，既不依赖批次（N），也不跨组共享统计量。
1. 通道分组：将 C 个通道分成 G 个组（需满足 C % G == 0），每组包含 C/G 个通道（记为 C_g = C/G）；
2. 统计量计算范围：对每个样本、每个通道组，收集该组内 C_g 个通道的所有空间像素（H×W 个），即范围为 (C_g, H, W)；
3. 归一化维度：对每个样本的每个通道组，将该组的 C_g×H×W 个元素归一化，且每个样本、每个组独立计算统计量。

三者的使用场景

归一化类型	核心适用场景关键词	批次依赖	通道 / 空间处理特点
BatchNorm	图像 CNN、大批次数据	强依赖（需 N≥8，推荐 N≥32）	单通道独立归一化，不跨通道
LayerNorm	NLP 序列任务、小批次 / 动态批次	无依赖（N=1 也可用）	跨通道 + 空间归一化（样本内全局 / 局部维度）
GroupNorm	图像 CNN（小批次）、医学图像（样本少）	无依赖	通道分组归一化（平衡通道关联性与计算效率）