Java 位运算算法题目练习

汉明距离

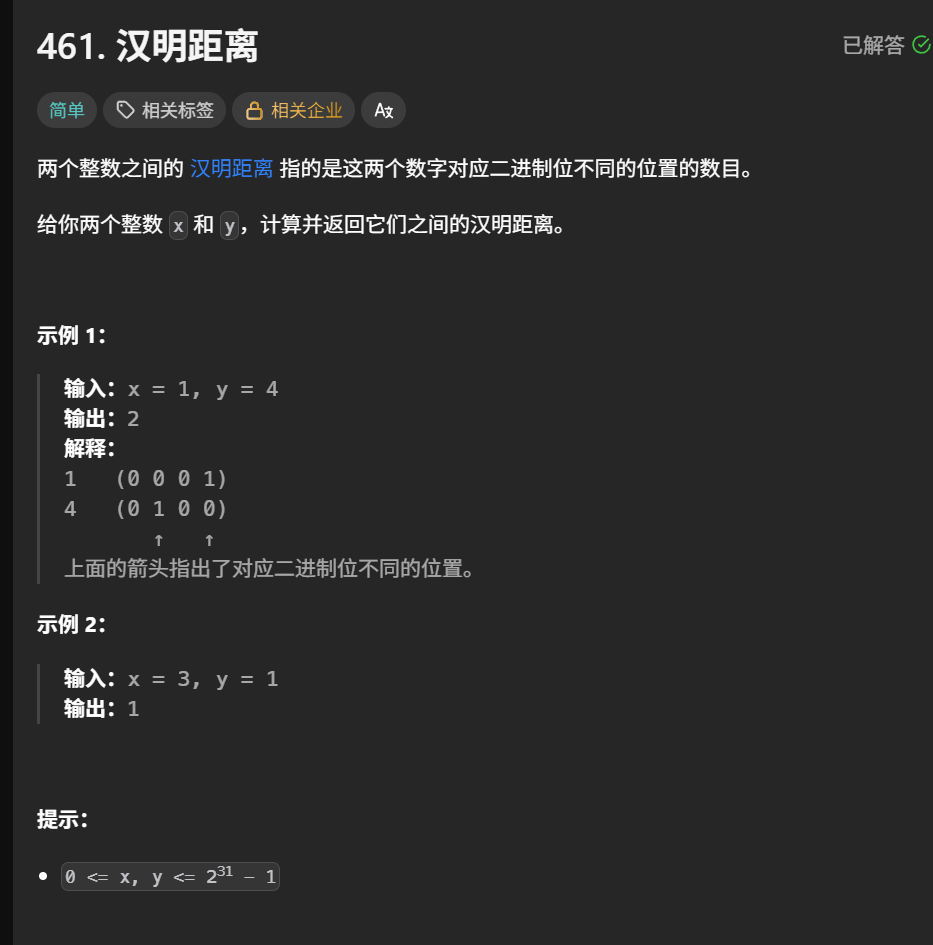
题目解析：判断两个数的对应的二进制位不同的个数
直接判断(x>>i)&1 和 （y>>i)&1，先获取对应二进制位，在判断是否相等即可

class Solution {public int hammingDistance(int x, int y) {int count = 0;//从后向前依次取出二进制位，进行比较for(int i = 0;i < 31;i++){if(((x>>i)&1) != ((y>>i)&1) ){count++;}}return count;}
}

比特位计数

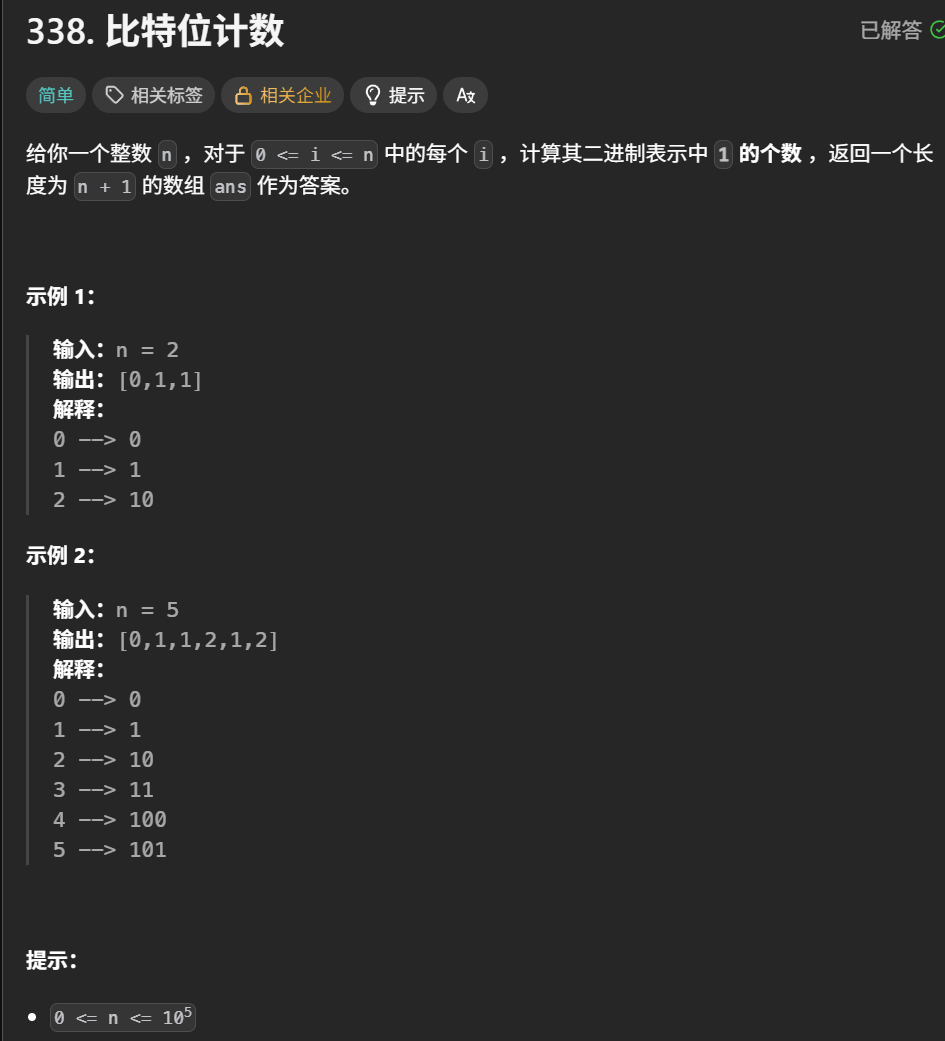
题目解析：给了一个数n，从[0,n]中，找出每一个数对应的二进制位中1的个数，并将其放一个长度为(n+1)数组中
暴力解法：因为 n & (n-1)每次都可以干掉最右边的1，这样每次遇到一个数，都进行这样的操作，直到这个数变成0，才进行下一个数的计算，时间复杂度：O(n * log n)
规律：一个正整数 x ,右移一位,将会去掉最低位，变成x / 2
但是我们可以知道，如果x是偶数其1的个数和x / 2是一样的,因为后面都是0
奇数的话就要+1
偶数：bits[x] = bits[x>>1]
奇数：bits[x] = bits[x>>1] + 1
通过这种方法可以利用前面已经计算过的数据，不用像上面重复计算
时间复杂度：O(n)

class Solution {public int[] countBits(int n) {//根据规律特性，偶数  bits[x]= bits[x/2] ，奇数+1int[] bits = new int[n+1];for(int i = 1;i<=n;i++){     }}
}

只出现一次的数字

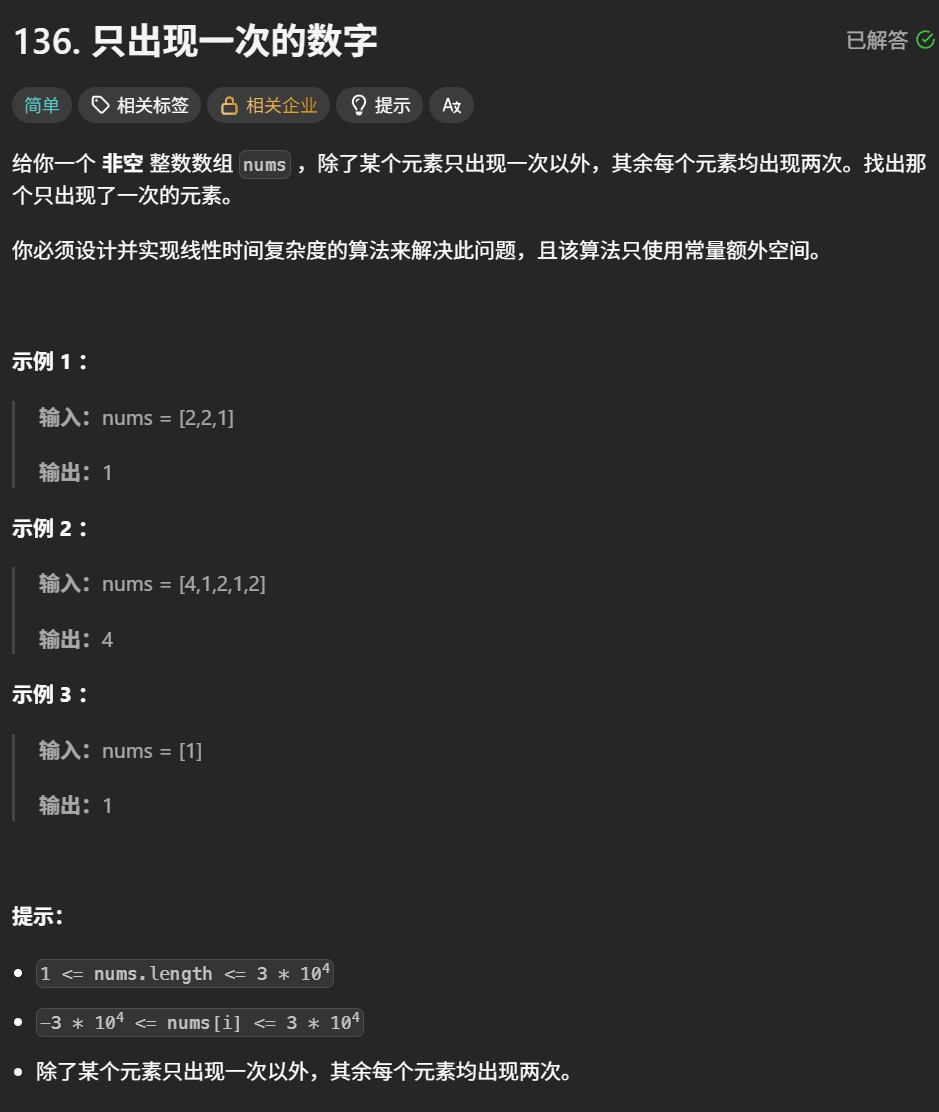
题目解析：一个数组中只有一个数出现一次，其他数都出现两次，找出这个出现一次的数
此可以使用异或，因为 a ^ a = 0，就这样将数组所有元素全部进行异或，最终的结果就是这个只出现一次的数

class Solution {public int singleNumber(int[] nums) {int ret = 0;for(int i = 0;i < nums.length;i++){ret ^= nums[i];}return ret;}
}

只出现一次的数字|||

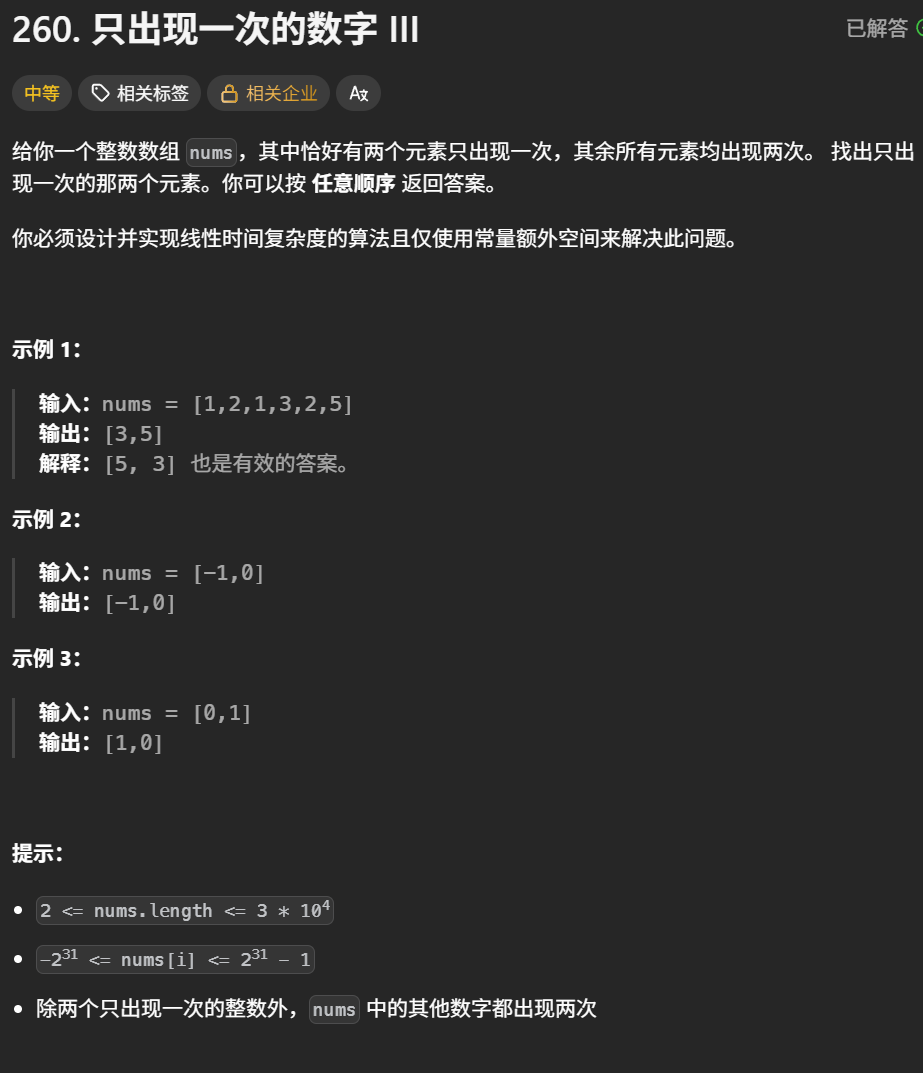
题目解析：上面那个题是找出只出现一次的一个数，但是这个题目中数组中又两个元素出现一次，其他都出现两次，找出这两个元素
思路：1.先进行全部数的异或，这样结果就是这两个出现一次的元素的异或结果，由于异或是相同为0，不同为1
2.因此我们只需将这个异或结果，在进行二次异或就行，当这个异或结果不为0，一个元素一直进行异或，当异或结果为0说明第二个数找到了，但是另一个这个要一直异或下去，这样第一个也找到了
3.细节，进行二次异或可能会出现数据溢出的情况，因此我们可以将2进行简化，因为异或的性质是相同为0，不同为1，当第一次异或中有一个二进制位是1，那说明这两个数肯定是一个是1，另一个是0，因此其实我们只拿第一次异或结果最右边的1进行异或即可 x & (-x)即可得到最右边的1

class Solution {public int[] singleNumber(int[] nums) {//先全部进行一次异或，这样得到的是其两个不同数的异或结果//因为 a^b^b = a//所以只需要在异或一遍int x = 0;for(int num : nums){x ^= num;}int t1 = 0;int t2 = 0;//防溢出    0x = x == Integer.MIN_VALUE ? x : x&(-x);for(int num : nums){if((num & x) != 0){t1 ^= num;}else{t2 ^= num;}}return new int[]{t1,t2};}
}

判断字符是否唯一

题目解析：有一个char类型的数组，里面存放的全是小写字母，判断其中是否有重复字母，如果有返回false,如果没有返回true
思路1：使用hash表，来遍历整个数组，每次放入元素都检查哈希表是否存放过这个元素，时间复杂度：O(n)，空间复杂度：O(n)
思路2：因为总共就26个小写英文字母，因此可以使用一个int[ ] 类型数组来模拟哈希表，这样空间复杂度变为O(1)
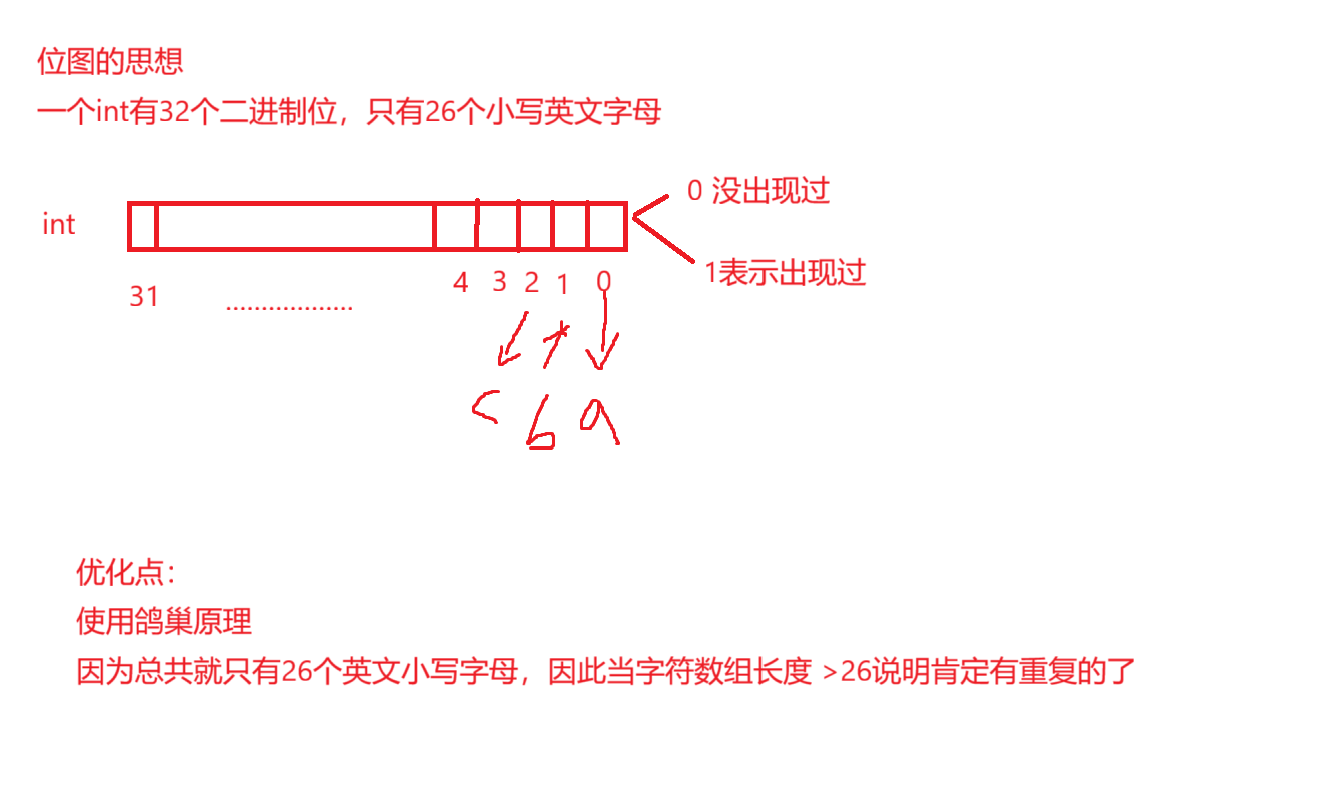
思路3：思路2其实还是有点浪费空间，因此我们可以使用位图，总共就26个小写英文字母，一个int类型有32个比特位，我们将小写字母对应到位图中，判断其对应的二进制位是否为1，为1返回false
不为1，将其对应的二进制位修改成1
if (((bitMap>>i)&1) == 1){
return false
}
bitMap |= (1 << x)

class Solution {public boolean isUnique(String astr) {if(astr.length() > 26){return false;}//位图的思想，只是用一个int来表示全部int bitMap = 0;for (int i = 0; i < astr.length(); i++) {int x = astr.charAt(i) - 'a';//判断其对应位置的二进制位是否为1if(((bitMap>>x)&1) == 1){return false;}//如果是0就将这个二进制位修改成1bitMap |= (1<<x);}return true;}
}

时间复杂度：O(n)
空间复杂度：O(1)

丢失的数字

题目解析：在[0 , n]中只有n个数在数组中，找出那个不在数字中的数

class Solution {public int missingNumber(int[] nums) {int ret = 0;for(int i = 0;i < nums.length;i++){ret ^= nums[i] ^ i;} //最后还有一个其长度没有异或return ret ^ nums.length;}
}

时间复杂度：O(n)
空间复杂度：O(1)

两数之和

题目解析：不适用+和-运算符计算两数之和
使用^(无进位相加)

class Solution {public int getSum(int a, int b) {//当没有进位a ^ b就是结果while(b != 0){int x = a ^ b;//无进位相加int carry = (a & b) << 1;  //计算进位a = x;b = carry;}return a;}
}

只出现一次的数字

题目解析：一个数组中只有一个数字出现一次，其他全部出现三次，找出这个只出现一次的数字
位图思想：一个一个二进制位确定，全部确定最终就得到这个数字
因此每次要计算出其数组每一个数值对应第 i 位 2进制之和，因为其他数字全部出现三次，因此让其 %3,得到的就是要找到数字第i 位 2进制的值

class Solution {public int singleNumber(int[] nums) {int ret = 0;for (int i = 0; i < 32; i++) {int sum = 0;//统计其数组第i位2进制之和for (int j = 0; j < nums.length; j++) {if (((nums[j] >> i) & 1) == 1) {sum++;}}sum %= 3;if (sum == 1) {//将其第i位修改成1ret |= (1 << i);}}return ret;}
}

时间复杂度：O(n ^ 2)
空间复杂度：O(1)

消失的两个数字

题目解析：一个包含[ 1, N]数的数组中有两个数消失了，找出这两个消失的数字
此题目结合 丢失的数字和只出现一次的数字|||的结合
丢失的数字：是找出一个数组缺失的一个数字
只出现一次的数字|||：是一个数组有两个数出现一次，其他全部出现两次，找出这两个只出现一次的数字
原理：1.先求出其消失的两个数字的异或结果，根据其丢失的数字这个题目，我们只需要将其nums数组所有元素和[0 , N]全部异或一起就是丢失两个数的异或结果记作ret
2.进行二次异或，找出这两个数，因为异或是相同为0，不同为1，所以只需要找出其任意一个ret中二进制位为1，这里可以先找出ret最右侧的1，拿这个来&进行判断，因为异或结果相同为0，不同为1，将其分为两类，一类是ret & 数 ！= 0，另一类==0，这样分别进行二次异或找出这两个数
也可以找出两个数异或结果ret中一个二进制位为1，拿这个二进制位分为两类，一类是这个二进制位为1，一类是这个二进制位为0，这个分为两类，分别异或最终可以找出这两个数

class Solution {public int[] missingTwo(int[] nums) {//先找出消失的两个数字^结果int ret = 0;for(int num : nums){ret ^= num;}for(int i = 1;i <= nums.length + 2;i++){ret ^= i;}//此时的ret就是消失的两个数字的异或结果//找出最右边的1ret = ret == 0 ? ret : ret&(-ret);//只根据其第i位进行判断即可，因为异或结果是相同为0，不同为1//此时将其分为两类int t1 = 0;int t2 = 0;for(int num : nums){if((ret & num) != 0){t1 ^= num;}else{t2 ^= num;}}for(int i = 1;i <= nums.length + 2;i++){if((ret & i )!= 0){t1 ^= i;}else{t2 ^= i;}}return new int[]{t1,t2};}
}

class Solution {public int[] missingTwo(int[] nums) {//先找出消失的两个数字^结果int ret = 0;for(int num : nums){ret ^= num;}for(int i = 1;i <= nums.length + 2;i++){ret ^= i;}//此时的ret就是消失的两个数字的异或结果int d = 0;//为1的二进制位while(true){if(((ret>>d)&1) == 1){break;}d++;}//只根据其第i位进行判断即可，因为异或结果是相同为0，不同为1//此时将其分为两类int t1 = 0;int t2 = 0;for(int num : nums){if(((num>>d) & 1)== 0){t1 ^= num;}else{t2 ^= num;}}for(int i = 1;i <= nums.length + 2;i++){if(((i>>d) & 1)== 0){t1 ^= i;}else{t2 ^= i;}}return new int[]{t1,t2};}
}