当前位置：首页 > news >正文

Dirichlet分布的理解与应用

news 2025/11/5 16:50:52

联邦学习中的非独立同分布数据模拟：Dirichlet分布原理与应用

Dirichlet分布基本原理

概念理解

Dirichlet分布可以被理解为"分布的分布"：它描述的是概率分布向量的分布特性。具体来说，Dirichlet分布研究的随机变量是一个 $N$ 维向量 $x=[x1,x2,...,xN]\boldsymbol{x} = [x_1, x_2, ..., x_N]$ ，其中每个元素 $x_i > 0$ 且满足 $∑i=1Nxi=1\sum_{i=1}^N x_i = 1$ ，因此可以视为一个概率分布。

举例说明：假设小明午餐会选择香蕉、苹果或梨这三种水果中的一种。我们可以用一个概率分布向量 $x=[0.2,0.4,0.4]\boldsymbol{x} = [0.2, 0.4, 0.4]$ 来描述他选择每种水果的概率，即选择香蕉的概率为0.2，选择苹果和梨的概率各为0.4。而Dirichlet分布研究的正是这种概率分布向量 $x\boldsymbol{x}$ 本身的分布特性。

数学形式

Dirichlet分布的概率密度函数形式如下：

$f(x∣αm)∝∏i=1Nxiαmi−1f(\boldsymbol{x}|\alpha\boldsymbol{m}) \propto \prod_{i=1}^N x_i^{\alpha m_i - 1}$

我们无需过度关注公式的细节，但需要理解该分布由参数 $u=αm\boldsymbol{u} = \alpha\boldsymbol{m}$ 控制，其中：

基向量 $m\boldsymbol{m}$ ：这是一个 $N$ 维向量，满足 $m_i > 0$ 且 $∑i=1Nmi=1\sum_{i=1}^N m_i = 1$ ，可以看作一个基准概率分布。该参数控制着 $x\boldsymbol{x}$ 的总体趋势。
浓度参数 $α\alpha$ ：这是一个正实数，控制着 $x\boldsymbol{x}$ 向基向量 $m\boldsymbol{m}$ 集中的程度。 $α\alpha$ 值越大， $x\boldsymbol{x}$ 越可能接近 $m\boldsymbol{m}$ 。

直观理解是：基向量 $m\boldsymbol{m}$ 提供了一个基准分布，而 $α\alpha$ 衡量了生成分布与这个基准的相似程度。值得注意的是， $m\boldsymbol{m}$ 实际上是随机向量 $x\boldsymbol{x}$ 的期望值，即 $E[x]=mE[\boldsymbol{x}] = \boldsymbol{m}$ 。

Dirichlet分布在联邦学习中的应用

在联邦学习的数据集划分中，我们可以利用Dirichlet分布生成不同类别数据在各个客户端上的分布比例向量 $x\boldsymbol{x}$ 。通常，我们将基向量 $m\boldsymbol{m}$ 设为均匀向量（即每个元素相等），通过调节浓度参数 $α\alpha$ 来控制生成的比例向量 $x\boldsymbol{x}$ 的均衡程度。

当 $α\alpha$ 很小时，生成的分布向量 $x\boldsymbol{x}$ 会显著偏离基向量 $m\boldsymbol{m}$ ，导致 $x\boldsymbol{x}$ 中各元素间差异较大，从而实现不同客户端上数据分布的非独立同分布特性。

实践应用

我们可以使用NumPy库中的numpy.random.dirichlet函数来生成各类别数据在不同客户端上的分布比例。

函数介绍

numpy.random.dirichlet(alpha, size=None)参数说明：

alpha：Dirichlet分布的参数，长度为 $K$ 的数组，表示分布的浓度参数
size：输出形状。如果为None，则返回单个 $K$ 维向量；如果给定形状，则返回该形状的数组，其中每个元素是一个 $K$ 维向量

返回值：从Dirichlet分布中采样的随机向量，形状由size参数决定

代码示例

以下代码展示了如何使用Dirichlet分布生成不同浓度参数下的样本，并可视化结果：

import numpy as np
import matplotlib.pyplot as plt# 定义三组不同的浓度参数α和基向量m的组合
# 注意：这里实际上定义的是α*m，即Dirichlet分布的完整参数
us = [(0.1, 0.1, 0.1), (1, 1, 1), (10, 10, 10)]  # 3组不同的u=alpha*m参数# 初始化存储采样点的列表
points = [[] for i in range(3)]# 对每组参数进行采样
for i in range(3):print(f"参数组 us[{i}]: {us[i]}")# 从Dirichlet分布中采样100个点points[i] = np.random.dirichlet(us[i], size=100)print(f"采样点 points[{i}] 的形状: {points[i].shape}")# 准备可视化数据：提取前两个维度用于二维散点图
xs, ys = [[] for i in range(3)], [[] for i in range(3)]for i in range(3):# 将三维点拆分为三个坐标列表，这里只取前两个维度用于绘图xs[i], ys[i], _ = list(zip(*points[i]))print(f"xs[{i}] 的前5个值: {xs[i][:5]}")print(f"ys[{i}] 的前5个值: {ys[i][:5]}")# 创建可视化图形
fig, axs = plt.subplots(1, 3, figsize=(12, 4), sharey=True)for i in range(3):axs[i].set_title(f"$αm={us[i]}$")axs[i].scatter(xs[i], ys[i], alpha=0.7)axs[i].set_xlabel("$X_1$")axs[i].set_ylabel("$X_2$")axs[i].set_xlim(0, 1)axs[i].set_ylim(0, 1)plt.suptitle(r"Dirichlet分布采样：$(X_1, X_2)$在$(X_1, X_2, X_3)$中的分布")
plt.tight_layout()
plt.show()

可视化结果分析

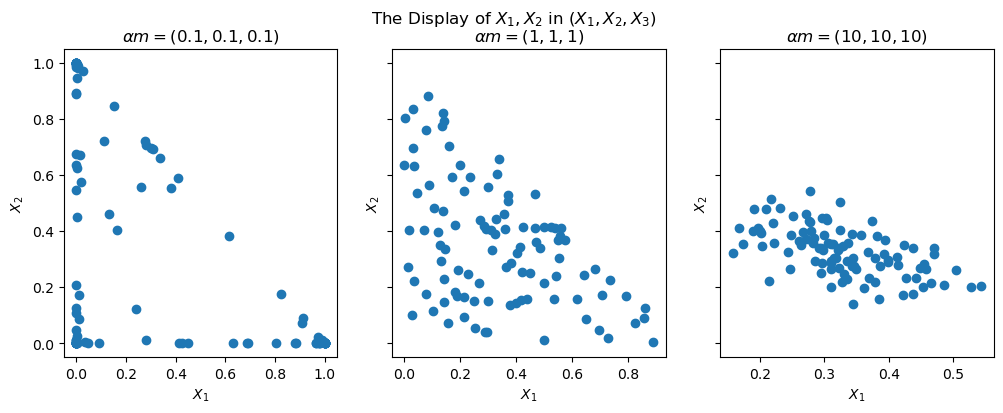
在这里插入图片描述

这三张图直观展示了Dirichlet分布的浓度参数 $α\alpha$ 对样本集中程度的控制作用：

当 $α\alpha$ 较小（如0.1）时，样本点分布较为分散，倾向于集中在单纯形的角落，这对应于联邦学习中高度非独立同分布的情况
当 $α\alpha$ 适中（如1）时，样本点分布相对均匀
当 $α\alpha$ 较大（如10）时，样本点高度集中于基向量 $m=(1/3,1/3,1/3)\boldsymbol{m}=(1/3,1/3,1/3)$ 附近，这对应于联邦学习中接近独立同分布的情况