算法学习入门---二分查找(C++)
目录
1.STL中的二分查找
2.牛客网---牛可乐和魔法封印
3.洛谷---A-B数对
4.洛谷---烦恼的高考志愿
5.洛谷---木材加工
6.洛谷---砍树
7.洛谷---跳石头
1.STL中的二分查找

lower_bound:大于等于 x 的最小元素,返回的是迭代器指针;时间复杂度为 O(logN)
使用时有3个参数,lower_bound(begin,end,target)
begin与end是查找的区间,左闭右开即 [begin,end),所以查找 a 数组 [1,8] 区间的target值,表示成 lower_bound(a+1,a+9,target)
upper_bound:大于 x 的最小元素,返回的是迭代器指针;时间复杂度为 O(logN)
返回的是大于x的最小元素迭代器,其他与lower_bound同
在使用迭代器时,可以使用auto类型来接受lower_bound返回的结果
然后对该结果进行解引用,即 auto it =lower_bound(begin,end,target),*it 即为it下标的值(相当于返回了一个只有一个值的数组)
注:STL中的二分算法只能对有序数组进行使用,使用的头文件为 algorithm
2.牛客网---牛可乐和魔法封印
非严格单调递增:递增的情况下,可以突然平一下,比如[1,2,2,3]
严格单调递增:递增的情况下,不能突然平一下
用二分查找左端点与二分查找右端点来解决问题(解决思路在leetcode二分查找中讲解了)
但需要注意的是几个特殊情况,因此该题不推荐使用lower_bound、upper_bound来完成,会使题目变得更加复杂(特殊情况在代码注释中有详细说明)
代码:
#include<iostream>
#include<vector>
using namespace std;int l_search(vector<long>& arr,long target)
{//需要特判,示例一中[-1,4]的情况int n = arr.size();if(target<arr[0]) return 0;int left=0,right=n-1;while(left<right){int mid = left+(right-left)/2;if(target>arr[mid]) left = mid+1;else right = mid;}return left;
}int r_search(vector<long>& arr,long target)
{int n = arr.size();//极限情况需要特判,例如示例一中的[2,6]if(target>arr[n-1]) return n-1; int left=0,right=n-1;while(left<right){int mid = left+(right-left+1)/2;if(target>=arr[mid]) left = mid;else right = mid-1;}return left;
}int main()
{int n;cin>>n;vector<long> arr(n,0);for(int i=0;i<=n-1;i++) cin>>arr[i];int q;cin>>q;for(int i=1;i<=q;i++) {long ret_left,ret_right;cin>>ret_left>>ret_right;if(ret_right<arr[0]||ret_left>arr[n-1]) cout<<0<<endl;//以示例一为例,[-1,0] [6,7] 结果都为0 else cout<<(r_search(arr,ret_right)-l_search(arr,ret_left)+1)<<endl;//返回的是数组下标,因此结果处需要+1 }return 0;
} 3.洛谷---A-B数对
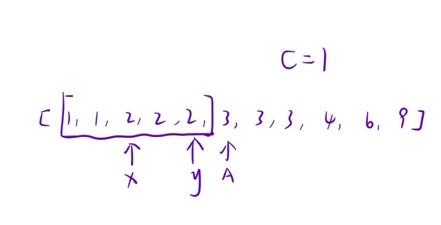
需要的结果是 A-B = C,可以转换为 B = C - A ,这样我们需要求的值就从2个变为了1个,然后找到第一个为B的,再找到最后一个为B的,统计这个区间有多少个B,然后对每个A进行该操作即可。(如下图所示)
此处可以用求左右端点的模板来解决该题,也可以使用upper_bound与lower_bound,因为该题的极限条件没有上一道题目那么多,所以建议使用后者
upper_bound:返回B所在的下标指针
lower_bound:返回比B刚好大1的下标指针,由于是针对 [0,i-1] 区间进行该操作(把 i 位置的元素视作A),所以即使返回了 i 位置的指针也依然满足条件
两个指针,可以通过指针相减的方式,直接获得结果值;只要注意循环从 1 位置 开始循环即可,因为数对数对,一定得是一对数才行,i 位置处的数即为数对中的一个数
同时还需要对原数组排序,排序完再使用两个二分stl库函数
代码:
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
#define int long longsigned main()
{int N,C;cin>>N>>C;vector<int> arr(N,0);for(int i=0;i<=N-1;i++)cin>>arr[i];sort(arr.begin(),arr.end());int ret = 0;for(int i=1;i<=N-1;i++){int A = arr[i]; auto x = lower_bound(arr.begin(),arr.begin()+i,A-C);auto y = upper_bound(arr.begin(),arr.begin()+i,A-C);ret+=(y-x);}cout<<ret;return 0;
}代码易错点:
upper_bound 和 lower_bound 中,如果要表示数组首元素,就必须以 arr.begin() 来表示,人为规定如此
4.洛谷---烦恼的高考志愿
排序+二分,可以使用lower_bound来辅助解决,需要注意的是score比最小的分数还要小以及比最大的分数还要大两种情况,特判完即可
代码:
#include<algorithm>
#include<vector>
#include<iostream>
#include<cmath>
using namespace std;
#define int long longsigned main()
{int m,n;cin>>m>>n;vector<int> schools(m,0);for(int i=0;i<=m-1;i++) cin>>schools[i];sort(schools.begin(),schools.end());int ret = 0;for(int i=1;i<=n;i++){int score;cin>>score;if(score<schools[0]) ret += (schools[0]-score);else if(score>schools[m-1]) ret += (score-schools[m-1]);else{auto it = lower_bound(schools.begin(),schools.end(),score);int school1 = *it;int school2 = *(it-1);if(fabs(score-school1)>fabs(score-school2)) ret+=fabs(score-school2);else ret+=fabs(score-school1);}}cout<<ret;return 0;
}算法题小诀窍:当发现类型错误时,#define int long long + int main 改为 signed main 可以解决大多数问题
5.洛谷---木材加工

如下图所示,以两根原木分别 11cm 和 21 cm 为例,每段切为5cm的话,即11cm的切出2段,21cm的切出4段,总共6段;如果每段切为4cm的话,可以切出7段,依旧满足条件,但不是最优解
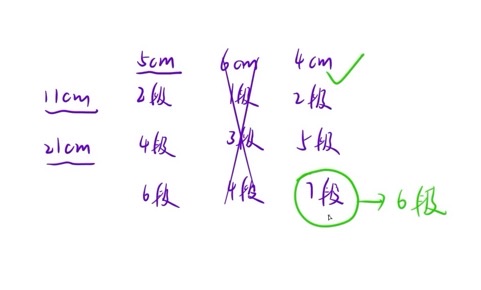
解法1:枚举从 0 cm到 maxlen cm(最长的一根原木的长度)的所有情况,每次判断一遍能切出多少段木头;对于第 i 根木头,可以切出 a[i] / x 段木头,所以假如 c 代表总的切出来的木段数,那么 c += a[i] / x(x为当前切的每段长度)
解法2:二分答案
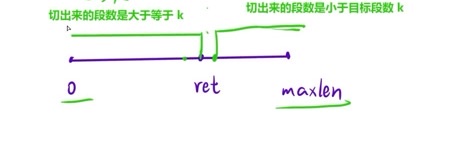
不难发现 x 与 c 成反比,当 x 为 maxlen 的时候只能切一段,为 1 时能且非常多段,这就是题目的二段性;如下图所示,c(切出来的段数)大于等于k时,说明 x 比较小落在了左边区间内;c 小于k时,说明 x 比较大落在了右边区间;当处于某个 x 值时,c 恰好处于 >=k 与 <k 的界限上,那么就是最后的ret,所以可以把题目转换为寻找区间右端点来解决
寻找区间右端点:left = mid and right = mid - 1,c >= k and c < k
c 的段数可以通过一个 caculator 函数来求出,通过模块性来降低代码的整体复杂度
总结:二分答案为从一堆答案当中,通过二分查找的方式找到最优解,它可以处理大部分[最小的最大值] 和 [最大的最小值] 问题,只要有二段性即可解决问题
代码:
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int caculator(vector<int>& a,int x)//统计段数
{int ret = 0;for(int i=0;i<=a.size()-1;i++)ret+=a[i]/x;return ret;
}int main()
{int n,k;cin>>n>>k;vector<int> forests(n,0);for(int i=0;i<=n-1;i++)cin>>forests[i];sort(forests.begin(),forests.end());int left=0,right=forests[n-1];while(left<right){int mid = left+(right-left+1)/2;if(caculator(forests,mid)>=k) left = mid;else right = mid - 1;}cout<<left;return 0;
}6.洛谷---砍树

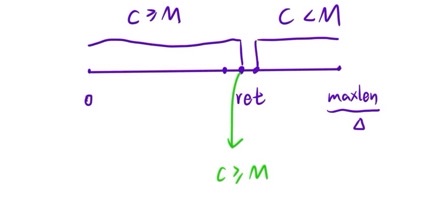
如下图所示,最优解是15cm高的电锯切一刀,20cm的切出5cm,17cm的切出2cm,最后刚好是要求的7cm,现在求这个电锯最高可以放在哪里切
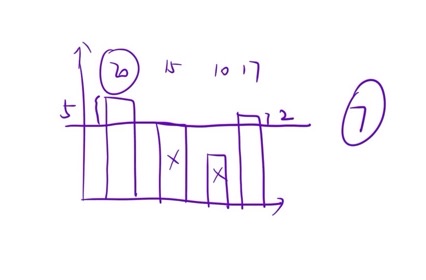
二分答案:
与上题解题思路大致相同,假设 h 表示当前电锯高度,c 表示当伐木机高度为 x 时能切出来的厘米数,则 h 与 c 成反比;所以 c >= M 时,h 在左区间,c < M 时,h 在右区间;对 [0,maxlen] 区间的值进行二分查找,maxlen 为最长的树木长度
根据上题的模板,只要把caculator函数稍微修改一下,就能够ac掉这道题了
注:本题数据大小会比较大,因此需要 #define int long long + signed main
代码:
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
#define int long long
int caculator(vector<int>& a,int x)//统计厘米
{int ret = 0;for(int i=0;i<=a.size()-1;i++)if(a[i]>x) ret+=(a[i]-x);return ret;
}signed main()
{int n,k;cin>>n>>k;vector<int> forests(n,0);for(int i=0;i<=n-1;i++)cin>>forests[i];sort(forests.begin(),forests.end());int left=0,right=forests[n-1];while(left<right){int mid = left+(right-left+1)/2;if(caculator(forests,mid)>=k) left = mid;else right = mid - 1;}cout<<left;return 0;
}7.洛谷---跳石头
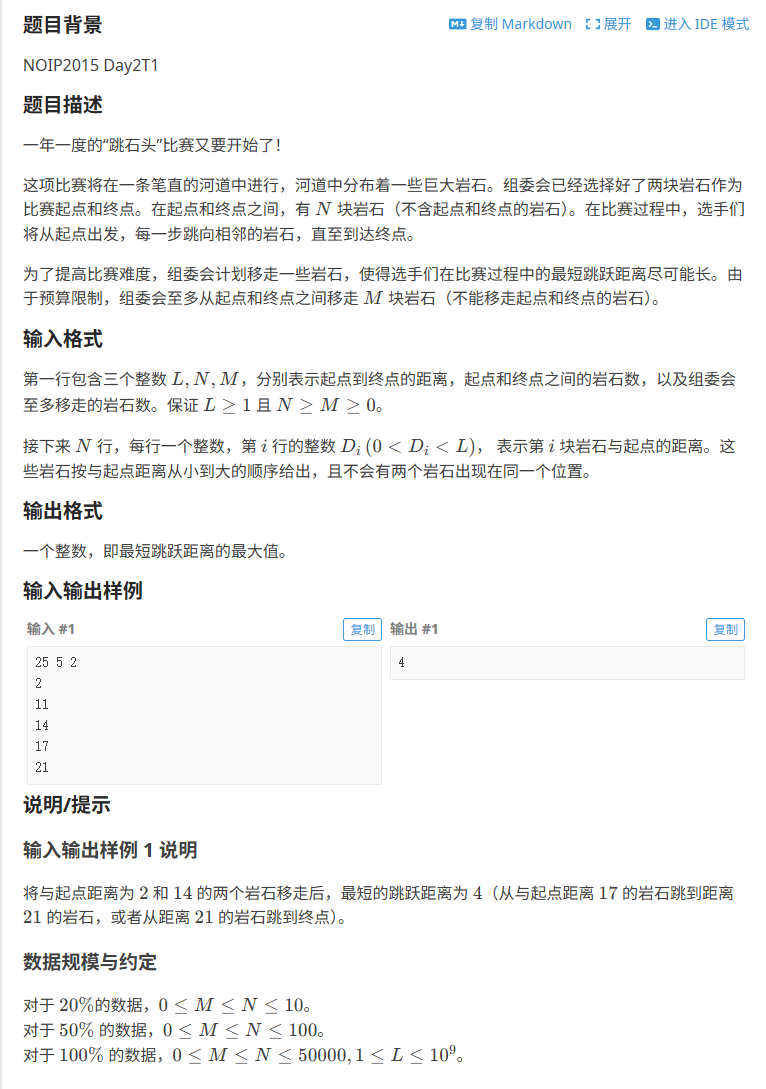
L距离之间有N+2块石头,现在可以从中移除2块(不能是第一块/最后一块),要求移除后 距离最近的两块相邻石头 距离最远,N行数分别代表距离第1块石头的距离
二分答案:
当我们看到最短跳跃距离要尽可能长的这种字眼,就要往 动态规划/二分答案/贪心 上面去思考
把 x 设为最短跳跃距离,c 设为跳跃距离为 x 下移走的岩石数目;假设把所有石头都移走,那么就得从起点一步跳到终点,通过该极限情况很容易发现 c 与 x 成正比
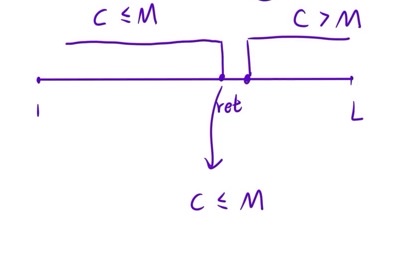
难点解析:
本题的难点在于,如何求出在跳跃距离为 x 的情况下,移走的岩石数目
可以通过一个双指针的方式来解决,定义双指针 i 、j ,初始都指向起点位置;然后 j 开始向后移动,直到移动到 a[j] - a[i] >= x 的情况下,此时 j - i - 1 即为所需移除的石头数量;然后 i 不要一步步往后移动到 j 位置,直接移到 j 位置即可,因为 i 移动时 j 已经处于最优的情况了,i 不断移动以后只会间隔越来越小,距离 x 也越来越远;最后对整个岩石数组重复该操作,并把每次情况统计到 ret 变量,因为 x 是最短跳跃距离,要所有的相邻石头都满足这个 x

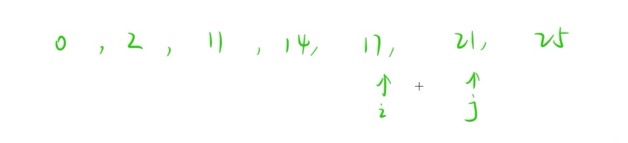
代码:
#include<iostream>
#include<vector>
#include<limits.h>
using namespace std;
#define int long long
int caculator(vector<int>& a,int x)
{int ret = 0;int i = 0,j = 0,n = a.size();while(i<=n-1){j = i;while(j<=n-1&&a[j]-a[i]<x)j++;ret += (j-i-1);i = j;}return ret;
}signed main()
{int L,N,M;cin>>L>>N>>M;vector<int> stones(N+2,0);stones[N+1] = L;for(int i=1;i<=N;i++) cin>>stones[i];//开始二分答案int left = 0,right = L;while(left<right){int mid = left+(right-left+1)/2;if(caculator(stones,mid)<=M) left = mid;else right = mid - 1;}cout<<left; return 0;
}代码易错点:
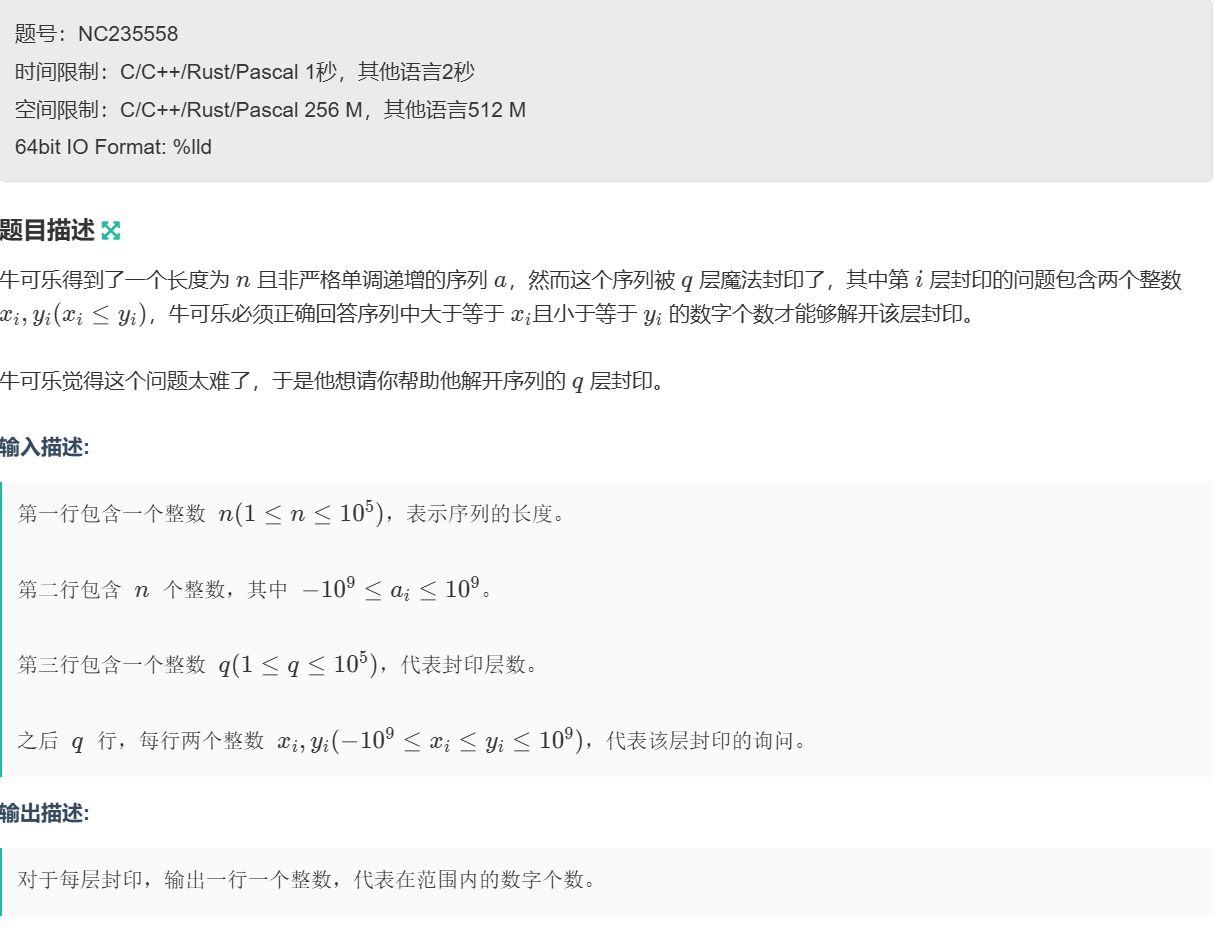
当 i = j = 3时,j 遍历完以后都没有把4、5两块石头给统计进去,同时最小的距离也不为 x ,14 与 25 之间只距离了 11,所以肯定出现逻辑错误;但我们可以假设把最后一块石头也给移出,这样14 与 +∞ 距离就能够大于 x 了,同时移除数量也是不会影响结果的