当前位置：首页 > news >正文

cf div2 1061个人补题笔记

news 2025/11/5 14:50:43

废话不多说，直接补题

A：

链接：Problem - A - Codeforces

思路：

最开始的总数是 $n$ ，由于每次的分配遵循 $m_{1} \leqslant m_{2} \leqslant m_{3}$ ，所以为了让 $m_{1}$ 尽可能大一点，每次分配保持 $m_{1}=m_{2}$ ，对于 $m_{3}$ 而言有以下几种情况：

（1）如果 $m_{3} \geqslant 3$ ，说明一定存在策略能把 $m_{3}$ 继续分配，保持 $m_{1}=m_{2}$ 。

（2）如果 $m_{3} <3$ ，说明 $m_{3}$ 无论怎么分配，都无法给 $m_{1}$ 分配数字。

因此，最终 $m_{1}$ 的最大值为 $\left \lfloor\frac{n-1}{2} \right \rfloor$

AC代码：

#include<bits/stdc++.h>
using namespace std;
int a[50];void solve(){int n;cin>>n;int ans=(n-1)/2;cout<<ans<<'\n';
}int main(){int t;cin>>t;while(t--){solve();}return 0;
}

B：

链接：Problem - B - Codeforces

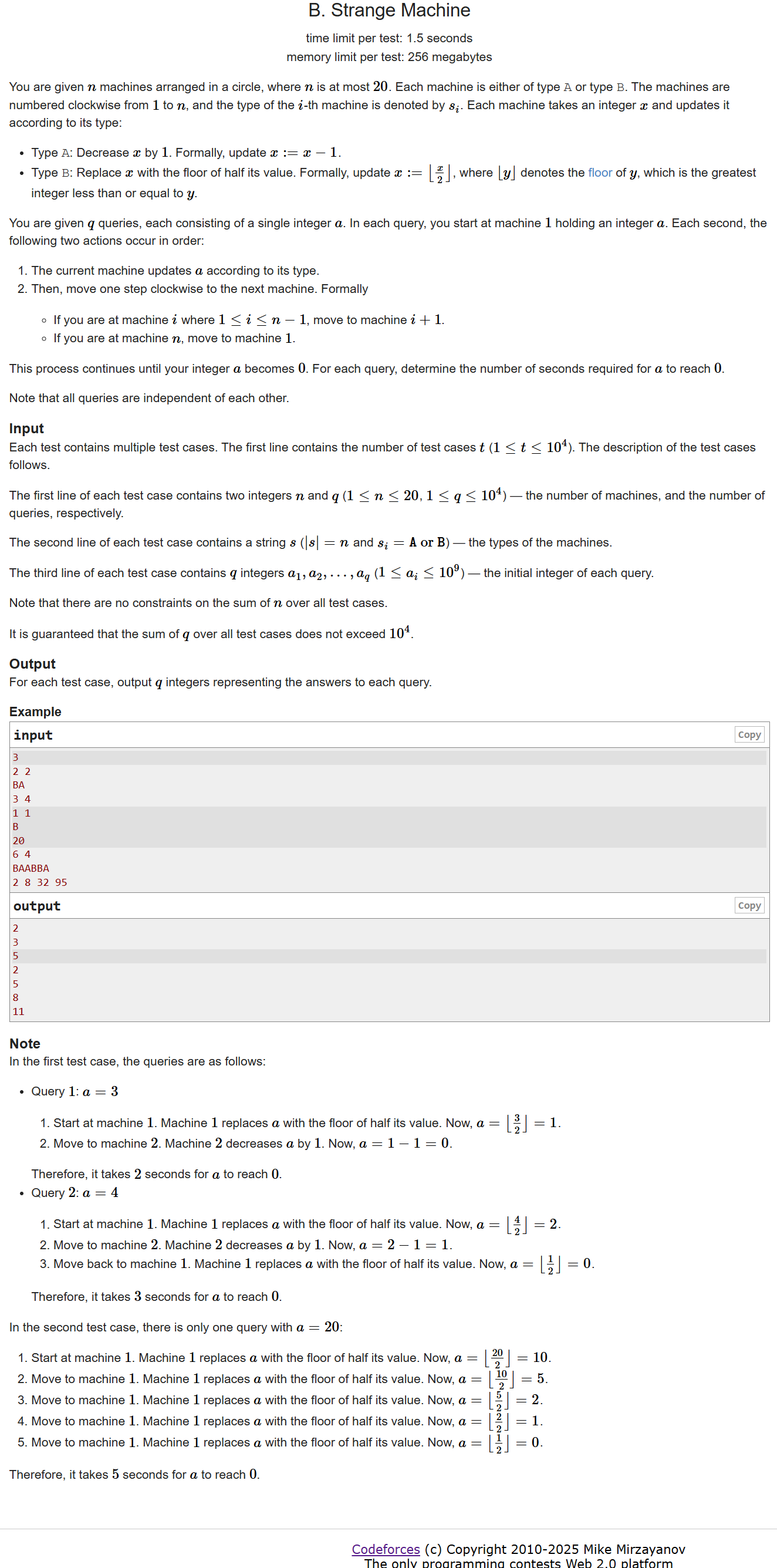
思路：

对于每一次查询，如果 $s$ 中存在 $B$ ，模拟过程即可，如果不存在直接输出对应的 $a_{i}$ 。

AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,q;
string s;
void solve(){cin>>n>>q;cin>>s;bool r=false;for(auto c:s){if(c=='B')r=true;}while(q--){int x;cin>>x;if(!r){cout<<x<<'\n';continue;}int id=0;int cnt=0;while(x){if(s[id]=='A')x--;elsex/=2;cnt++;id=(id+1)%n;}cout<<cnt<<'\n';}
}int main(){int t;cin>>t;while(t--){solve();}return 0;
}

C：

链接：Problem - C - Codeforces

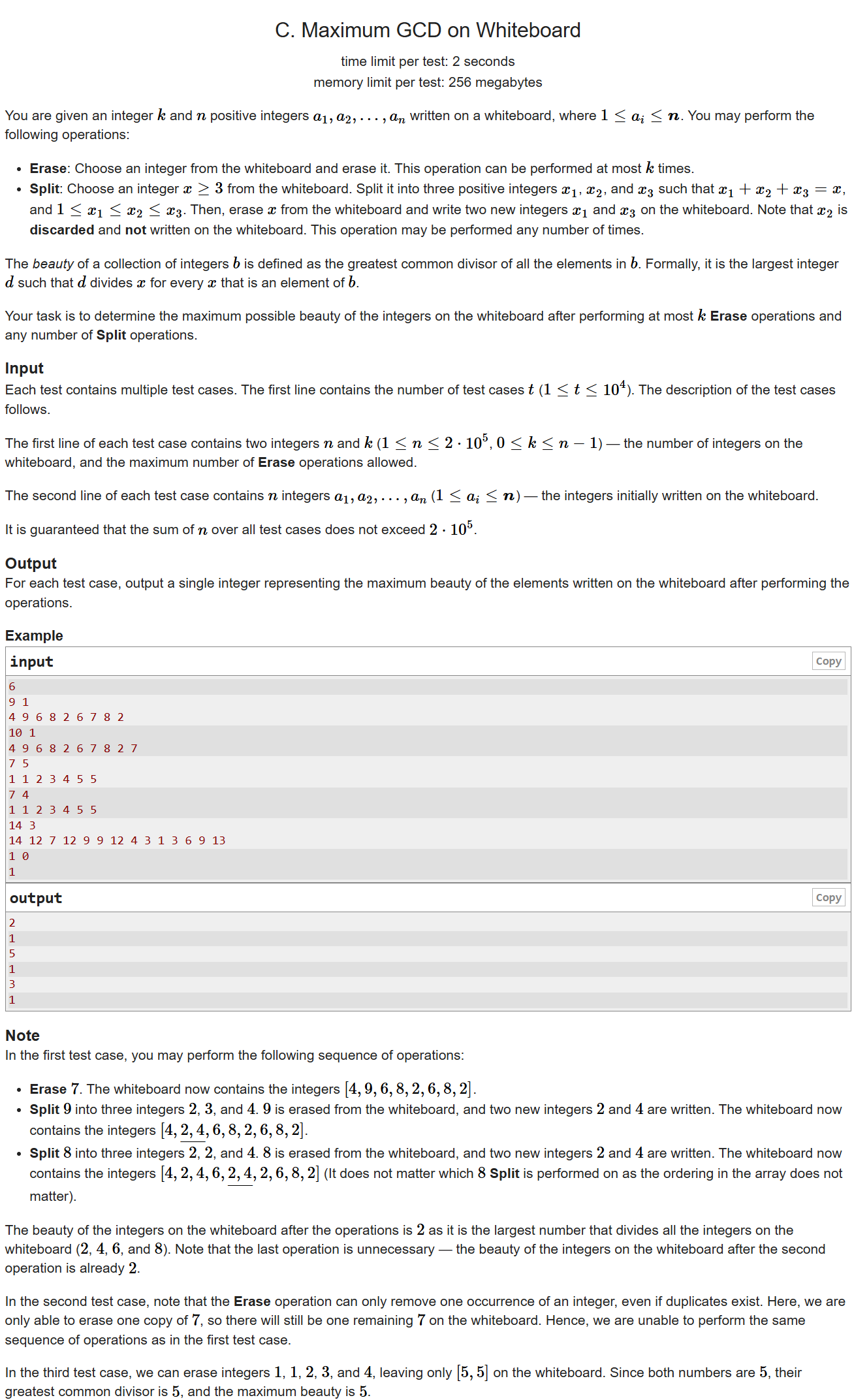
思路：

对于这道题而言，直接从数组出发其实是不好考虑的，我们不妨从最终的答案 $d$ 出发考虑。

可以容易知道，对于每一个可能的答案 $d$ ，若 $a_{i} \geqslant 4d$ ，则 $a_{i}$ 必然可以通过 $Split$ 操作让其变成 $d$ 的倍数，否则必然不可能通过 $split$ 操作，就需要 $Erase$ 操作让非 $d$ 倍数的 $a_{i}$ 消失。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+100;
int n,k;
int sum[N],a[N];
void solve(){for(int i=1;i<=4*n;i++)a[i]=sum[i]=0;cin>>n>>k;int ans=1;for(int i=1;i<=n;i++){int x;cin>>x;a[x]++;}for(int i=1;i<=4*n;i++)sum[i]=sum[i-1]+a[i];for(int i=1;i<=n;i++){int s=sum[4*i-1];s-=a[i]+a[2*i]+a[3*i];if(s<=k)ans=max(ans,i);}cout<<ans<<'\n';
}int main(){int t;cin>>t;while(t--){solve();}return 0;
}

D：

链接：Problem - D - Codeforces

思路：

对于一个排列 $1\sim n$ ，假设对 $n$ 二进制拆位有 $k$ 位。

从第 $1$ 位开始拆位，大致有 $\frac{n}{2}$ 的数第 $1$ 位是 $1$ ，有 $\frac{n}{2}$ 的数第 $1$ 位是 $0$ 。

从第 $2$ 位开始拆位，最多有 $\frac{n}{2}$ 的数第 $1$ 位是 $1$ ，有 $\frac{n}{2}$ 的数第 $1$ 位是 $0$ 。

但既满足第 $1$ 位其中一个条件又满足第 $2$ 位其中一个条件的只有 $\frac{n}{4}$ 个数字，对于更高位也是同理。

这样对于查询而言，最多查询 $\frac{n}{2^{0}} +\frac{n}{2^{1}} +\frac{n}{2^{2}}+ ......+\frac{n}{2^{k}} = \frac{\frac{1}{2}*(1-(\frac{1}{2})^{k+1})}{\frac{1}{2}}*n = (1-(\frac{1}{2})^{k+1})*n < n$ 次。

具体实现上开两个 bool 类型数组 $num$ （记录不可能的数字，如果 $num[i] = true$ 代表 $i$ 这个数字不可能是结果）和 $id$ （记录没有帮助的下标，如果 $id[i] = true$ 代表 $i$ 这个下标对于结果的查询没有帮助）。

对于第 $i$ 轮， $num[a_{j}] = false$ 的值中，分别记录 $2^{i-1}$ & $a_{j} > 0$ 的数量 $x_{1}$ 和 $2^{i-1}$ & $a_{j} = 0$ 的数量 $x_{2}$ 。

然后对于 $id_{j} = false$ 的下标中，分别进行查询，若是 $a_{id_{j}}$ & & $2^{i-1} > 0$ ，则 $x_{1}=x_{1}-1$ ,否则 $x_{2}=x_{2}-1$ 。

最后 $x_{1}=0 ~or~x_{2}=0$ ，若是 $x_{1}=0$ 则把 $1\sim n$ 中 $2^{i-1}$ && $a_{i} > 0$ 中的 $num [a_{i}]= true$ ，并且把 $a_{id_{j}}$ & & $2^{i-1} > 0$ 中的 $id_{i}=true$ 。

反之则把 $1\sim n$ 中 $2^{i-1}$ && $a_{i} = 0$ 中的 $num [a_{i}]= true$ ，并且把 $a_{id_{j}}$ & & $2^{i-1}= 0$ 中的 $id_{i}=true$ 。

然后进行第 $i-1$ 轮操作，直至查询操作前 $x_{1}~+~x_{2} ~ =~1$ 实现即终止。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+100;
int n;int print(int id,int x){cout<<"? "<<id<<" "<<x<<'\n';int r;cin>>r;return r;
}
bool num[N],id[N];void solve(){cin>>n;for(int i=1;i<=n;i++)num[i]=id[i]=false;int r=1;while(1){int x1,x2;x1=x2=0;for(int i=1;i<=n;i++){if(num[i])continue;if((i&r))x1++;elsex2++;}if(x1+x2==1)break;vector<int>c1,c2;for(int i=1;i<n;i++){if(id[i])continue;if(print(i,r)){x1--;c1.push_back(i);}else{x2--;c2.push_back(i);}}if(!x1){//说明 最后一位 第 k位为0for(int i=1;i<=n;i++)if((i&r))num[i]=true;for(auto a:c1)id[a]=true;}else {for(int i=1;i<=n;i++)if(!(i&r))num[i]=true;for(auto a:c2)id[a]=true;}r*=2;}for(int i=1;i<=n;i++)if(!num[i]){cout<<"! "<<i<<'\n';return ;}
}int main(){int t;cin>>t;while(t--){solve();}return 0;
}

E：

链接：Problem - E - Codeforces

思路：

我们可以考虑一件事情，最终美丽数的大小由锁定的几个数来决定，其中真正做贡献的只有2个数字，因此，其实锁的操作只需要进行4步即可确定答案（因为经过4步操作后总能让美丽数达到Alex的预期，后续的操作其实不影响最终结果），然后我们就需要考虑如何进行这4步了。

我们如果通过枚举数组来直接找答案其实是很难的，因为枚举的话就需要 $n^{2}$ 的复杂度，很明显是会超时的，其实我们根据4步操作这个性质就操作。

我们可以二分一个预想的结果 $d$ ，然后对 $d$ 进行检验，具体思想如下：

对于 $i<j$ ，若是 $x_{j} -x_{j}\geqslant d$ ，则说明这一对可以，我们可以对 $i$ 、 $j$ 建边，最终构成一张图，保证这张图删除一个节点后还存在一个度为2以上的节点。

对于每一个 $j$ ，我们可以只保留满足 $i<j$ 的3个最小 $x_{i}$ 处理即可。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
typedef long long ll;
typedef pair<ll,int> PII;
const ll inf=1e9+100;
vector<int>eg[N];
ll a[N];
int n;bool check(ll x){for(int i=1;i<=n;i++)eg[i].clear();vector<PII>cun;for(int i=1;i<=n;i++){for(auto [val,id]:cun){if(a[i]-val>=x){eg[i].push_back(id);eg[id].push_back(i);}}cun.push_back({a[i],i});sort(cun.begin(),cun.end());if(cun.size()>3)cun.pop_back();}    int cnt=0;for(int i=1;i<=n;i++)if(eg[i].size()>=2)cnt++;for(int i=1;i<=n;i++){int res=eg[i].size()>=2;for(auto v:eg[i]){if(eg[v].size()==2)res++;}if(res==cnt)return false;}return true;
}void solve(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];ll l=-inf,r=inf;ll ans;while(l<=r){ll mid=(l+r)/2;if(check(mid)){ans=mid;l=mid+1;}elser=mid-1;}cout<<ans<<'\n';
}int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t;cin>>t;while(t--){solve();}return 0;
}

至于后续的F1、F2，等我有能力了再补，打上欠条先。

查看全文

http://www.dtcms.com/a/570523.html