归并排序解读(基于java实现)
归并排序(Merge Sort)是一种基于分治思想的排序算法,它的核心思想是将待排序序列分为若干个子序列,然后对每个子序列进行排序,最终合并成完整的有序序列。
归并排序可以按照以下步骤进行:
- 将待排序序列拆分为两个子序列,分别对这两个子序列递归地进行归并排序。
- 将两个排好序的子序列合并成一个有序序列。合并时,需要使用额外的辅助数组,以便在合并过程中保存排好序的元素。
- 重复步骤1和步骤2,直到所有子序列都被排好序并合并成一个完整的有序序列。
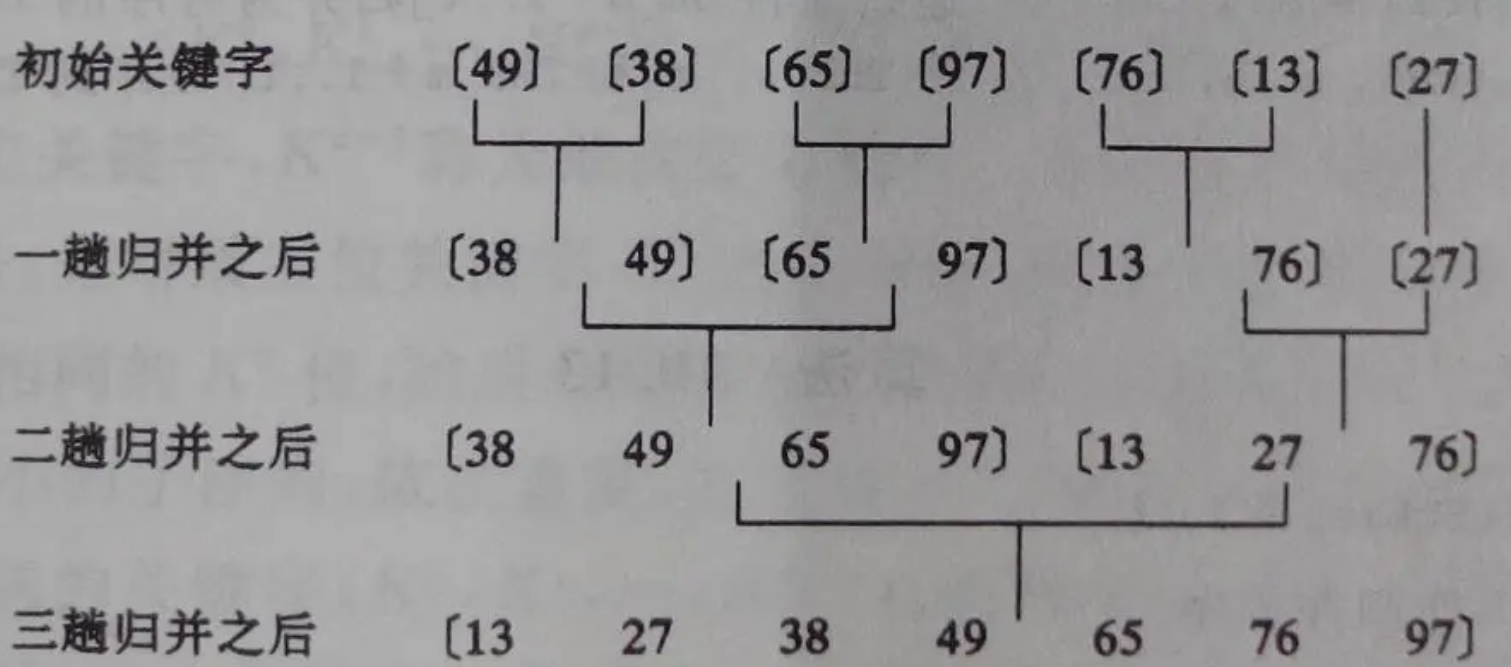
时间复杂度:
分解:首先将待排序序列不断二分,直到每个子序列只有一个元素,这个过程的时间复杂度为O(logn),因为每次都将序列分成两半,需要进行logn次。
合并:对于每一层的合并操作,需要将相邻的子序列合并成一个有序序列,这个过程的时间复杂度为O(n),因为需要比较和移动n个元素。
总体来说,在归并排序的每一层中,合并操作都需要进行n次,而分解操作的次数是logn。所以,总的时间复杂度可以表示为O(nlogn)。
空间复杂度:
归并排序的空间复杂度为O(n),其中n表示待排序序列的长度。
在每一层的合并操作中,都需要使用额外的辅助数组来暂存排序结果。这个辅助数组的大小与待排序序列的长度相等。由于在整个排序过程中,会存在多层递归,每一层都会创建一个辅助数组。所以,归并排序的空间复杂度是O(n)。
注意点:归并排序的空间复杂度是以代价换取了时间复杂度的优化,因为它需要额外的存储空间来存放辅助数组。在实际应用中,如果内存空间有限,可能需要考虑归并排序的空间消耗。
伪代码如下:
代码语言:java
AI代码解释
MergeSort(arr, left, right)if left < rightmid = (left + right) / 2// 分解:将待排序序列二分为两个子序列MergeSort(arr, left, mid) // 对左侧子序列进行归并排序MergeSort(arr, mid + 1, right) // 对右侧子序列进行归并排序// 合并:将两个排好序的子序列合并为一个有序序列Merge(arr, left, mid, right)Merge(arr, left, mid, right)n1 = mid - left + 1n2 = right - mid// 创建临时数组来存放排序结果L[n1], R[n2]// 将数据拷贝到临时数组for i = 0 to n1L[i] = arr[left + i]for j = 0 to n2R[j] = arr[mid + 1 + j]i = 0, j = 0, k = left// 合并两个有序子序列while i < n1 and j < n2if L[i] <= R[j]arr[k] = L[i]i++elsearr[k] = R[j]j++k++// 将剩余元素直接拷贝到排序数组while i < n1arr[k] = L[i]i++k++while j < n2arr[k] = R[j]j++k++
MergeSort函数用于分解和合并操作,它首先将待排序序列二分为两个子序列,然后对每个子序列递归地调用MergeSort函数进行排序。最后,调用Merge函数将两个排好序的子序列合并成一个有序序列。
Merge函数用于合并操作,它创建了临时数组来存放排序结果,并在合并过程中比较和移动元素。它首先将待合并的两个子序列拷贝到临时数组中,然后按照大小顺序将元素依次放回原始数组。最后,将剩余的元素直接拷贝到原始数组中。
基于java实现:
代码语言:java
AI代码解释
public class MergeSort {public void mergeSort(int[] arr) {if (arr == null || arr.length <= 1) {return;}mergeSort(arr, 0, arr.length - 1);}private void mergeSort(int[] arr, int left, int right) {if (left < right) {int mid = (left + right) / 2;mergeSort(arr, left, mid); // 对左侧子序列进行归并排序mergeSort(arr, mid + 1, right); // 对右侧子序列进行归并排序merge(arr, left, mid, right); // 合并两个有序子序列}}private void merge(int[] arr, int left, int mid, int right) {int n1 = mid - left + 1;int n2 = right - mid;// 创建临时数组来存放排序结果int[] L = new int[n1];int[] R = new int[n2];// 将数据拷贝到临时数组for (int i = 0; i < n1; i++) {L[i] = arr[left + i];}for (int j = 0; j < n2; j++) {R[j] = arr[mid + 1 + j];}int i = 0, j = 0, k = left;// 合并两个有序子序列while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;} else {arr[k] = R[j];j++;}k++;}// 将剩余元素直接拷贝到排序数组while (i < n1) {arr[k] = L[i];i++;k++;}while (j < n2) {arr[k] = R[j];j++;k++;}}public static void main(String[] args) {int[] arr = {12, 11, 13, 5, 6, 7};MergeSort sorter = new MergeSort();sorter.mergeSort(arr);for (int num : arr) {System.out.print(num + " ");}}
}