【LeetCode】98. 验证二叉搜索树

98. 验证二叉搜索树

题目描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 严格小于 当前节点的数。
节点的右子树只包含 严格大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

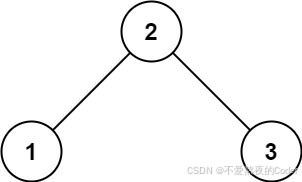
输入：root = [2,1,3]
输出：true

示例 2：

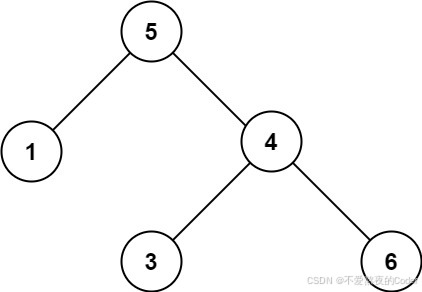
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 10^4] 内
• -2^31 <= Node.val <= 2^31 - 1

解题思路

问题深度分析

这是经典的二叉树验证问题，也是BST性质的典型应用。核心在于验证BST的三个约束条件：左子树严格小于根节点，右子树严格大于根节点，且左右子树本身也是BST。

问题本质

给定一个二叉树，判断它是否满足BST的定义。这是一个树遍历问题，需要验证每个节点都满足BST的性质。

核心思想

BST的性质验证：

1. 上下界约束：每个节点必须在合理的上下界范围内
2. 递归验证：左右子树必须也是BST
3. 中序递增性：BST的中序遍历结果必须是严格递增的
4. 严格性：左子树严格小于，右子树严格大于（不能等于）

关键技巧：

• 使用递归传递上下界（min, max）
• 利用中序遍历的递增性质
• 处理整数边界问题（使用指针或特殊值）
• 注意严格性的要求（< 和 >，不是 <= 和 >=）

关键难点分析

难点1：上下界的传递

• 需要为每个节点维护合理的上下界
• 左子树的上界是父节点值，下界继承父节点
• 右子树的下界是父节点值，上界继承父节点
• 需要处理整数边界（-2^31 到 2^31-1）

难点2：严格性的要求

• 左子树必须严格小于父节点（<）
• 右子树必须严格大于父节点（>）
• 不能使用 <= 或 >=，否则会错误接受重复值

难点3：中序遍历的递增性

• BST的中序遍历必须是严格递增的
• 需要记录前一个访问的节点值
• 需要处理边界情况（第一个节点）

典型情况分析

情况1：有效BST

     2/ \1   3

• 节点2：范围(-∞, +∞)，值2在范围内 ✓
• 节点1：范围(-∞, 2)，值1 < 2 ✓
• 节点3：范围(2, +∞)，值3 > 2 ✓
  结果：true

情况2：无效BST（右子树小于根）

     5/ \1   4/ \3   6

• 节点5：范围(-∞, +∞)，值5在范围内 ✓
• 节点1：范围(-∞, 5)，值1 < 5 ✓
• 节点4：范围(5, +∞)，值4 < 5 ✗（违反BST性质）
  结果：false

情况3：无效BST（左子树大于根）

     5/ \6   7

• 节点5：范围(-∞, +∞)，值5在范围内 ✓
• 节点6：范围(-∞, 5)，值6 > 5 ✗（违反BST性质）
  结果：false

情况4：无效BST（重复值）

     2/ \2   3

• 节点2：范围(-∞, +∞)，值2在范围内 ✓
• 左节点2：范围(-∞, 2)，值2 < 2 ✗（违反严格性）
  结果：false

算法对比

算法	时间复杂度	空间复杂度	特点
递归上下界	O(n)	O(h)	最优解法，直观易懂
中序遍历递归	O(n)	O(h)	利用BST性质，经典方法
中序遍历迭代	O(n)	O(n)	避免递归栈溢出
Morris遍历	O(n)	O(1)	空间最优，但会修改树

注：n为节点数，h为树高度

算法流程图

主算法流程（递归上下界）

graph TDA[isValidBST(root)] --> B{root==nil?}B -->|是| C[return true]B -->|否| D[检查root.Val是否在范围内]D --> E{min < root.Val < max?}E -->|否| F[return false]E -->|是| G[递归验证左子树]G --> H[递归验证右子树]H --> I{左右子树都有效?}I -->|是| J[return true]I -->|否| F

上下界传递流程

中序遍历验证流程

graph TDA[inorder(root)] --> B{root==nil?}B -->|是| C[return]B -->|否| D[inorder(root.Left)]D --> E{prev != nil?}E -->|是| F{prev.Val < root.Val?}F -->|否| G[标记无效]F -->|是| H[更新prev]E -->|否| HH --> I[inorder(root.Right)]I --> J[继续遍历]G --> J

复杂度分析

时间复杂度详解

递归上下界算法：O(n)

• 每个节点最多被访问一次
• 每次访问进行常数时间检查
• 总时间：O(n)

中序遍历算法：O(n)

• 需要遍历所有节点
• 每次访问检查与前一个节点的关系
• 总时间：O(n)

空间复杂度详解

递归上下界算法：O(h)

• 递归调用栈深度为树高度
• 最坏情况（链状树）：O(n)
• 最好情况（平衡树）：O(log n)

中序遍历迭代算法：O(n)

• 需要显式栈存储节点
• 最坏情况栈大小为n
• 总空间：O(n)

Morris遍历算法：O(1)

• 只使用常数额外空间
• 通过修改树指针实现遍历
• 总空间：O(1)

关键优化技巧

技巧1：递归上下界验证（最优解法）

func isValidBST(root *TreeNode) bool {return isValidBSTHelper(root, nil, nil)
}func isValidBSTHelper(node *TreeNode, min, max *int) bool {if node == nil {return true}// 检查当前节点值是否在范围内if min != nil && node.Val <= *min {return false}if max != nil && node.Val >= *max {return false}// 递归验证左右子树// 左子树：上界更新为当前节点值// 右子树：下界更新为当前节点值return isValidBSTHelper(node.Left, min, &node.Val) &&isValidBSTHelper(node.Right, &node.Val, max)
}

优势：

• 时间复杂度：O(n)
• 空间复杂度：O(h)
• 逻辑清晰，易于理解
• 使用指针避免整数边界问题

技巧2：中序遍历递归验证

var prev *intfunc isValidBST(root *TreeNode) bool {prev = nilreturn inorder(root)
}func inorder(root *TreeNode) bool {if root == nil {return true}// 验证左子树if !inorder(root.Left) {return false}// 检查当前节点if prev != nil && root.Val <= *prev {return false}prev = &root.Val// 验证右子树return inorder(root.Right)
}

特点：利用BST中序遍历递增的性质，代码简洁

技巧3：中序遍历迭代验证

func isValidBST(root *TreeNode) bool {stack := []*TreeNode{}cur := rootvar prev *intfor cur != nil || len(stack) > 0 {// 一路向左for cur != nil {stack = append(stack, cur)cur = cur.Left}// 访问节点n := len(stack) - 1node := stack[n]stack = stack[:n]// 检查递增性if prev != nil && node.Val <= *prev {return false}prev = &node.Val// 转向右子树cur = node.Right}return true
}

特点：避免递归，适合深度很大的树

技巧4：Morris遍历验证

func isValidBST(root *TreeNode) bool {cur := rootvar prev *intfor cur != nil {if cur.Left == nil {// 访问当前节点if prev != nil && cur.Val <= *prev {return false}prev = &cur.Valcur = cur.Right} else {// 寻找前驱节点pre := cur.Leftfor pre.Right != nil && pre.Right != cur {pre = pre.Right}if pre.Right == nil {// 建立线索pre.Right = curcur = cur.Left} else {// 拆除线索并访问pre.Right = nilif prev != nil && cur.Val <= *prev {return false}prev = &cur.Valcur = cur.Right}}}return true
}

特点：空间复杂度O(1)，但会临时修改树结构

边界条件处理

边界情况1：空树

• 处理：空树不是有效的BST（根据题目约束，节点数>=1）
• 但为安全考虑：可以返回true或false，根据题目要求

边界情况2：单节点树

• 处理：单个节点总是有效的BST
• 验证：值在(-∞, +∞)范围内 ✓

边界情况3：整数边界

• 处理：使用指针(*int)而不是int值传递边界
• 原因：需要区分"无边界"和"边界值为-2^31或231-1"
• 替代方案：使用特殊值或更大的数据类型

边界情况4：重复值

• 处理：严格检查 < 和 >，不允许 <= 和 >=
• 示例：如果左子节点值等于父节点，应该返回false

边界情况5：极端不平衡树

• 处理：递归方法可能栈溢出（但题目约束节点数<=10^4，通常不会）
• 优化：使用迭代方法避免栈溢出

测试用例设计

基础测试用例

1. 有效BST：[2,1,3] → true
2. 无效BST（右子树小于根）：[5,1,4,null,null,3,6] → false
3. 空树：[] → true（或根据题目要求）
4. 单节点：[1] → true

进阶测试用例

5. 重复值：[2,2,3] → false
6. 左子树大于根：[5,6,7] → false
7. 完全BST：[4,2,6,1,3,5,7] → true
8. 链状BST：[1,null,2,null,null,null,3] → true
9. 边界值：包含-2^31和2^31-1的BST
10. 深度不平衡：极端左偏或右偏的BST

常见错误和陷阱

错误1：使用 <= 和 >= 而不是 < 和 >

// 错误写法
if node.Val <= min || node.Val >= max {return false
}// 正确写法
if node.Val < min || node.Val > max {return false
}

原因：BST要求严格小于和严格大于

错误2：整数边界处理不当

// 错误写法：使用int传递边界
func isValidBSTHelper(node *TreeNode, min, max int) bool {// 无法区分"无边界"和"边界值为0"
}// 正确写法：使用指针
func isValidBSTHelper(node *TreeNode, min, max *int) bool {// 可以区分nil（无边界）和具体值
}

错误3：中序遍历时忘记更新prev

// 错误写法
if prev != nil && root.Val <= *prev {return false
}
// 忘记更新prev// 正确写法
if prev != nil && root.Val <= *prev {return false
}
prev = &root.Val  // 必须更新

错误4：Morris遍历后未恢复树结构

• 问题：Morris遍历会修改树指针，但遍历过程中会恢复
• 注意：如果在遍历中断，需要手动恢复

实用技巧

1. 优先使用递归上下界方法：逻辑清晰，易于理解和调试
2. 处理整数边界：使用指针或更大的数据类型（如int64）
3. 注意严格性：牢记BST的严格小于/大于要求
4. 中序遍历方法：适合需要同时验证多个BST性质的情况
5. 迭代方法：适合深度很大的树，避免栈溢出
6. Morris遍历：适合空间受限的场景

进阶扩展

扩展1：验证BST并返回错误信息

• 不仅返回true/false，还返回具体的错误节点和原因

扩展2：修复无效BST

• 将无效BST转换为有效BST（可能需要重建树）

扩展3：验证BST的多种定义

• 有些定义允许相等值，有些不允许
• 需要根据具体定义调整验证逻辑

扩展4：并行验证

• 对于大型树，可以使用并行算法加速验证

应用场景

1. 数据库索引验证：验证B树/B+树索引是否有效
2. 数据结构验证：验证树结构是否符合BST定义
3. 算法正确性检查：验证BST构建算法的正确性
4. 代码审查：检查BST相关代码的实现
5. 树结构修复：在修复无效BST前先验证

总结

验证BST是一个经典的树遍历问题，核心在于：

1. 理解BST的定义：左子树严格小于，右子树严格大于
2. 选择合适的方法：递归上下界最直观，中序遍历利用性质
3. 注意边界条件：整数边界、空树、重复值
4. 严格性要求：必须使用 < 和 >，不能使用 <= 和 >=

完整题解代码

package mainimport ("fmt"
)type TreeNode struct {Val   intLeft  *TreeNodeRight *TreeNode
}// =========================== 方法一：递归上下界验证（最优解法） ===========================
func isValidBST1(root *TreeNode) bool {return isValidBSTHelper1(root, nil, nil)
}func isValidBSTHelper1(node *TreeNode, min, max *int) bool {if node == nil {return true}// 检查当前节点值是否在范围内（严格小于/大于）if min != nil && node.Val <= *min {return false}if max != nil && node.Val >= *max {return false}// 递归验证左右子树// 左子树：上界更新为当前节点值// 右子树：下界更新为当前节点值return isValidBSTHelper1(node.Left, min, &node.Val) &&isValidBSTHelper1(node.Right, &node.Val, max)
}// =========================== 方法二：中序遍历递归验证 ===========================
var prev2 *intfunc isValidBST2(root *TreeNode) bool {prev2 = nilreturn inorder2(root)
}func inorder2(root *TreeNode) bool {if root == nil {return true}// 验证左子树if !inorder2(root.Left) {return false}// 检查当前节点（中序遍历，此时访问根节点）if prev2 != nil && root.Val <= *prev2 {return false}prev2 = &root.Val// 验证右子树return inorder2(root.Right)
}// =========================== 方法三：中序遍历迭代验证 ===========================
func isValidBST3(root *TreeNode) bool {if root == nil {return true}stack := []*TreeNode{}cur := rootvar prev *intfor cur != nil || len(stack) > 0 {// 一路向左for cur != nil {stack = append(stack, cur)cur = cur.Left}// 访问节点n := len(stack) - 1node := stack[n]stack = stack[:n]// 检查递增性（BST中序遍历必须严格递增）if prev != nil && node.Val <= *prev {return false}prev = &node.Val// 转向右子树cur = node.Right}return true
}// =========================== 方法四：Morris遍历验证 ===========================
func isValidBST4(root *TreeNode) bool {if root == nil {return true}cur := rootvar prev *intfor cur != nil {if cur.Left == nil {// 访问当前节点if prev != nil && cur.Val <= *prev {return false}prev = &cur.Valcur = cur.Right} else {// 寻找前驱节点（左子树的最右节点）pre := cur.Leftfor pre.Right != nil && pre.Right != cur {pre = pre.Right}if pre.Right == nil {// 建立线索pre.Right = curcur = cur.Left} else {// 拆除线索并访问当前节点pre.Right = nilif prev != nil && cur.Val <= *prev {return false}prev = &cur.Valcur = cur.Right}}}return true
}// =========================== 工具函数：构建二叉树 ===========================
func arrayToTreeLevelOrder(arr []interface{}) *TreeNode {if len(arr) == 0 {return nil}if arr[0] == nil {return nil}root := &TreeNode{Val: arr[0].(int)}queue := []*TreeNode{root}i := 1for i < len(arr) && len(queue) > 0 {node := queue[0]queue = queue[1:]// 左子节点if i < len(arr) && arr[i] != nil {left := &TreeNode{Val: arr[i].(int)}node.Left = leftqueue = append(queue, left)}i++// 右子节点if i < len(arr) && arr[i] != nil {right := &TreeNode{Val: arr[i].(int)}node.Right = rightqueue = append(queue, right)}i++}return root
}// =========================== 测试 ===========================
func main() {fmt.Println("=== LeetCode 98: 验证二叉搜索树 ===\n")testCases := []struct {name     stringroot     *TreeNodeexpected bool}{{name:     "例1: [2,1,3] - 有效BST",root:     arrayToTreeLevelOrder([]interface{}{2, 1, 3}),expected: true,},{name:     "例2: [5,1,4,null,null,3,6] - 无效BST",root:     arrayToTreeLevelOrder([]interface{}{5, 1, 4, nil, nil, 3, 6}),expected: false,},{name:     "单节点 - 有效BST",root:     arrayToTreeLevelOrder([]interface{}{1}),expected: true,},{name:     "[1,1] - 重复值，无效BST",root:     arrayToTreeLevelOrder([]interface{}{1, 1}),expected: false,},{name:     "[2,2,3] - 左子节点重复，无效BST",root:     arrayToTreeLevelOrder([]interface{}{2, 2, 3}),expected: false,},{name:     "[5,6,7] - 左子节点大于根，无效BST",root:     arrayToTreeLevelOrder([]interface{}{5, 6, 7}),expected: false,},{name:     "[4,2,6,1,3,5,7] - 完全BST，有效",root:     arrayToTreeLevelOrder([]interface{}{4, 2, 6, 1, 3, 5, 7}),expected: true,},{name:     "[1,null,2,null,null,null,3] - 右链BST，有效",root:     arrayToTreeLevelOrder([]interface{}{1, nil, 2, nil, nil, nil, 3}),expected: true,},{name:     "[10,5,15,null,null,6,20] - 右子树中有小于根的值，无效",root:     arrayToTreeLevelOrder([]interface{}{10, 5, 15, nil, nil, 6, 20}),expected: false,},{name:     "[3,1,5,0,2,4,6] - 复杂有效BST",root:     arrayToTreeLevelOrder([]interface{}{3, 1, 5, 0, 2, 4, 6}),expected: true,},}methods := map[string]func(*TreeNode) bool{"递归上下界验证":  isValidBST1,"中序遍历递归":   isValidBST2,"中序遍历迭代":   isValidBST3,"Morris遍历": isValidBST4,}for methodName, methodFunc := range methods {fmt.Printf("方法：%s\n", methodName)pass := 0for i, tc := range testCases {got := methodFunc(tc.root)ok := got == tc.expectedstatus := "✅"if !ok {status = "❌"}fmt.Printf("  测试%d(%s): %s\n", i+1, tc.name, status)if !ok {fmt.Printf("    输出: %v\n    期望: %v\n", got, tc.expected)} else {pass++}}fmt.Printf("  通过: %d/%d\n\n", pass, len(testCases))}
}