当前位置：首页 > news >正文

电路分析 | Phasor Analysis（篇 1）

news 2025/11/5 7:51:10

注：本文为 “电路分析 | Phasor Analysis” 相关论文合辑。
图片清晰度受引文原图所限。
略作重排，如有内容异常，请看原文。

相量法历史上的三篇经典文献

张亮亮雷银照
(北京航空航天大学自动化科学与电气工程学院北京 100191)

收稿日期 2011-03-16 改稿日期 2011-07-13

摘要

研究了促成相量法提出的三篇文献，分别探讨了它们的主要内容、成文背景和历史地位。结果表明：1886 年 7 月，亥维赛在分析外加振荡电动势的效应及其在长途电话和电报信号传输中的应用时，首次提出“阻抗”术语，并将它定义为传输线上外加电动势振幅和电流振幅之比；1893 年 4 月，肯涅利将亥维赛定义的传输线的阻抗推广到一般交流电路和设备的阻抗，并使用复数表示阻抗；1893 年 8 月，施泰因梅茨为了分析通用电气公司为尼亚加拉瀑布水电站设计的三相系统中相间的不平衡现象，在肯涅利使用复数表示阻抗的基础上，用复数表示正弦电压和正弦电流，提出了相量法。

关键词

相量法；阻抗；亥维赛；肯涅利；施泰因梅茨；历史

中图分类号：TM13

1 引言

相量法是计算线性电路的一种简便有效的数学方法。它的提出是电气发展史上的一件大事，推动了电路理论的快速发展，对 19 世纪 80 至 90 年代交流电的普及起到了决定性作用，促使交流设备迅速商品化。翻开今天电工学科的教科书可以看到，相量法已成为电类学生的必学内容。

历史上，有三篇文献对该方法的建立起到了至关重要的作用。1886 年 7 月 23 日，英国电气工程师亥维赛发表了论文“线路一端外加振荡电动势的效应及其在长途电话和电报信号传输中的应用”[1]，针对传输线问题进行了探讨，首次提出“阻抗”一词，对分析和计算交流电路起到了开创性的作用。以此为基础，美国电气工程师肯涅利在 1893 年 4 月 18 日宣读的一篇论文“阻抗”[2]中使用复数表示阻抗，详细研究了有关阻抗计算的一些问题。受这篇论文启发，美国电气工程师施泰因梅茨在 1893 年 8 月宣读的著名论文“复数及其在电气工程领域的应用”[3]中使用复数表示正弦电压和正弦电流，提出了一种计算交流电路的重要方法-相量法。

研究这三篇文献的内容、地位及背景，有助于我们理清相量法的历史脉络，为相量法的教学提供历史背景资料，使电类学生更准确地理解相量法，从而更好地运用相量法。同时，本文的研究将为进一步研究相量法在中国电工学科中的传播、交流理论及交流系统发展史中的其他问题提供参考。

国家自然科学基金资助项目(51077002)。收稿日期 2011-03-16；改稿日期 2011-07-13

2 亥维赛首次提出“阻抗”一词的论文

2.1 亥维赛简介及其论文概况

亥维赛[4,5]（见图 1），1850 年 5 月 18 日出生于英国伦敦的卡姆登，1925 年 2 月 3 日逝世于英国德文郡的托基。他是一位自学成才的数学物理学家，一生最主要的成就是：整理简化了麦克斯韦方程组；发展了传输线理论，建立了电报方程并求出其解；独立于肯涅利预言电离层的存在；推导出坡印亭定理；提出了运算微积分法(类似于现在使用的拉普拉斯变换法)；独立于美国科学家吉布斯(J. W. Gibbs, 1839-1903 年)提出了矢量分析法；首次提出电导(conductance; 1885 年 9 月)、磁导率(permeability; 1885 年 9 月)、电感(inductance; 1886 年 2 月)、阻抗(impedance; 1886 年 7 月)、电纳(permittance; 1887 年 6 月)、导纳(admittance; 1887 年 12 月)、磁阻(reluctance; 1888 年 5 月)等电磁学术语。

在这里插入图片描述
图 1 亥维赛(1850-1925 年)(图片取自文献[6])
Fig.1 O. Heaviside (1850-1925) (source of image: [6])

亥维赛的这篇论文（见文献[1]）起初刊于英国《电学家》杂志，后收录到亥维赛所著的 1892 年出版的《电学论文集》，全文共 6 页。

在交流电路中研究者曾使用“交流电阻”(alternating-current resistance)或“表观电阻”(apparent resistance)等名称[7]来对应直流电路的“电阻”，这两种名称的英文均是两个单词，而该文提出了一个更简捷的名称“阻抗”(impedance)，只对应一个英文单词。1889 年在巴黎召开的国际电气会议采纳了“阻抗”术语[8]，此后电工界开始广泛使用。

同时，文中首次定义了交流传输线的阻抗，这样人们就可以用它来综合考虑线路中电阻、电感和电容这三个参数的效应，从而有助于建立交流电路的欧姆定律，对分析和计算交流电路起到重要的推动作用，为相量法的提出做了准备。

2.2 成文背景

亥维赛在青年时代就注重电信技术的理论探讨[5]。从事电报员工作时，亥维赛曾接到一项测量电报信号传输速度的任务，他发现从英格兰发送到丹麦比从丹麦发送到英格兰的电报的速度快 40%，这个奇怪的现象引起了他的兴趣，之后便投入大量时间从理论上研究电报和电话信号的传输问题。1873 年，当他获得英国物理学家麦克斯韦(J. C. Maxwell, 1831-1879 年)的巨著《电磁通论》时，被麦克斯韦的电磁场理论吸引，遂想精通此书以推广该理论。经过长达十几年的研究，1885 年他将麦克斯韦的 20 个标量形式电磁场方程简化为 4 个不完全对称的矢量方程，随后应用它们来解决电报和电话信号的传输问题。其间，他研究了传输线一端外加振荡电动势的效应，撰写了文献[1]。

2.3 论文内容

文献[1]主要包括两部分。

第一部分：分析了线路上加与不加电动势时线路的表面电位 $v$ 与电流 $C$ （现用 $I$ ）的变化，在此基础上，定义了不考虑静电感应时传输线的阻抗。这是该文的重要内容，其中首次提出“阻抗”并给出定义（见图 2）：“当一条线路上的静电感应可忽略时，我们将其外加电动势和电流之比称为该线路的阻抗。”

文中还给出一些特定情形下的阻抗：①直流传输线的阻抗等于电阻 $Rl$ 。②对于交流传输线，频率非常低时阻抗等于电阻 $Rl$ ；频率较高时阻抗为 $(R2+L2n2)12l(R^{2}+L^{2} n^{2})^{\frac{1}{2}} l$ ，式中 $R$ 和 $L$ 分别表示线路的单位长电阻和电感， $n$ （现用 $ω\omega$ ）为正弦波的角频率， $l$ 为线路长度。

在这里插入图片描述
图 2 亥维赛在文献[1]中给出的阻抗定义
Fig.2 The definition of impedance in [1] by Heaviside

第二部分：在考虑静电感应的条件下，定义传输线的阻抗。由于考虑静电感应时电流振幅从外加电动势处到线的远端逐渐变小，所以线路阻抗也相应变化。此时若将阻抗的定义限制于外加电动势处，则必须再创造一个新词，因此亥维赛延伸了阻抗的定义，将 $V_{0}/C_{0}$ 的含义扩展到线路上任一点，其中 $V_{0}$ （现用 $V_{m}$ ）表示外加电动势的振幅， $C_{0}$ （现用 $I_{m}$ ）表示线路上电流的振幅。

可见，亥维赛将阻抗定义为外加电动势振幅和电流振幅之比[9]，在定义中他提到了阻抗模，但未提及阻抗角。

提出“阻抗”一词后，亥维赛又引入交流电路的“电阻算子”(resistance operator)，并用符号 $Z$ 表示，该词的含义和符号表示等同现在使用的“阻抗”[10,11]。

3 肯涅利研究阻抗问题的论文

“阻抗”一词提出后不久，电工界便开始广泛使用它，为了更好地理解和使用该词，当时正从事交流研究工作的肯涅利在亥维赛的研究基础上，进一步研究了有关阻抗计算的问题。

3.1 肯涅利简介及其论文概况

肯涅利[12-14]（见图 3），1861 年 12 月 17 日出生于印度孟买附近的戈拉巴，1939 年 6 月 18 日逝世于美国麻省波士顿。他是一位著名的电气工程师和物理学家，主要贡献有：用复数表示交流电路的阻抗；独立于亥维赛预言电离层的存在，电离层的 E 区曾称为“肯涅利–亥维赛层”；积极致力于国际电磁单位和标准的演变研究，曾担任美国公制学会会长和美国电机工程师学会标准委员会主席等职务。
在这里插入图片描述
图 3 肯涅利(1861-1939 年)(图片取自文献[15])
Fig.3 A. E. Kennelly (1861-1939) (source of image: [15])

肯涅利的论文（见文献[2]）在 1893 年 4 月 18 日召开的美国电机工程师学会的第 76 次会议上宣读，随后刊登在该年出版的《美国电机工程师学会会刊》上，全文共 42 页。

肯涅利在文中指出，如果交流电采用正弦波，就可以引入“阻抗”概念，结合使用复数，交流电路就可以和直流电路一样利用欧姆定律计算。

该文将阻抗概念从传输线推广到一般交流电路，首次基于阻抗三角形[16]使用复数分析交流电路，为使用复数方法计算交流电路奠定了基础，推动了交流电路理论的发展。

3.2 成文背景

在“交直流大战”期间，为了证明交流电比直流电危险，爱迪生(T. A. Edison, 1847-1931 年)想了各种办法。1887 年 12 月，他雇佣刚来美国的肯涅利在其西奥兰治实验室进行交流研究[17]。1888 年 7 月至 12 月，爱迪生派肯涅利指导布朗(H. P. Brown, 1869-1932 年)对狗和其他动物进行交流电刑实验，执行电刑的电椅正是在此基础上研制出来的[17,18]。由于肯涅利了解爱迪生为抵制交流电所采取的一些手段，所以他在文献[2]中强调说“目前为掩盖交流电的工作原理而制造的种种困难，在很大程度上都是虚构的、编造的”。从 1887 年到 1893 年，肯涅利发表了一些关于交流电的论文，并在爱迪生实验室设计了一个实验交流系统。对交流电的这些分析以及实际问题的需要促使他研究了交流电路的阻抗，撰写了文献[2]。

3.3 论文内容

论文[2]由正文、会上对论文的讨论、会后施泰因梅茨对论文的评论等部分组成①。

①《美国电机工程师学会会刊》早期刊登的论文一般都是先在美国电机工程师学会的会议上宣读，而后在会上讨论，所以在刊出时一些论文的正文后附有讨论，个别还附有会后对论文所做的书面评论。

3.3.1 正文第一部分：阻抗及其计算

“一个导体的阻抗就是其表观电阻，它的量纲为欧姆。严格来说，阻抗已被定义为导体端子间的有效电动势和导体的有效电流强度之比。”肯涅利将“阻抗”推广到表示交流电路和设备的端电压振幅与电流振幅之比。他进而指出直流电路和交流电路阻抗的特点，并给出交流电路的欧姆定律： $C = E / I$ ，式中 $E$ （现用 $U$ ）、 $C$ （现用 $I$ ）、 $I$ （现用 $Z$ ）分别表示电压、电流和阻抗。

通过使用阻抗三角形和平行四边形法则，肯涅利系统介绍了 $R L$ 电路、 $RC$ 电路、 $R L C$ 电路的阻抗以及阻抗并联后的总阻抗的计算。由此他得出结论：阻抗为电阻和电感速度(inductance-speed)及电容速度倒数(capacity-speed-reciprocal)的合成。

3.3.2 正文第二部分：使用复数表示阻抗

肯涅利总结说：“当阻抗或其倒数的和与差都以矢量形式处理时，并且如果所有交流电都严格用正弦波表示，所有电感都是非铁磁性的，那么由欧姆定律所得到的所有关于直流电的结论，也适用于正弦交流，从而就可以像在直流电路中那样来考虑交流电路中电压和电流的关系。”在此基础上，他指出其论文的核心思想-使用复数表示阻抗（见图 4）：“若将电感视为 $\sqrt{-1}$ 形式的电阻，将电容视为 $−1kp−1-\frac{1}{k p} \sqrt{-1}$ 形式的电阻，则任何包含电阻、非铁磁性电感和电容的正弦交流电路都可以使用直流规则处理，相应的代数运算按照‘复数’的运算法则进行。”

在这里插入图片描述

图 4 肯涅利论文的核心思想(取自文献[2])
Fig.4 The main idea of Kennelly’s paper (source: [2])

施泰因梅茨没有参加肯涅利宣读论文[2]的会议，会后他对该文有一个书面评论，强调了其核心思想并指出将复数引入交流理论分析的重要性：“若用复数 $j=r(\cos \varphi+j \sin \varphi)$ 表示阻抗，则任何包含电阻、非铁磁性电感和电容的正弦交流电路都可以使用直流规则处理，相应的代数运算按照复数的运算法则进行。”

据我所知，在这篇论文中，肯涅利率先在电气术语‘阻抗’和复数之间建立了一种对应关系。其重要性在于：研究者关于复平面的分析已比较透彻，因此，将电气问题转化为对复数的分析，就将它们带到一个已知的、理解得比较好的科学领域。”

4 施泰因梅茨提出相量法的论文

施泰因梅茨注意到分析交流电路的图形法和肯涅利提出的复阻抗几何表示法之间具有相似性，于是将这两种方法结合起来，4 个月后提出了一个完整的复数方法-相量法来求解交流电路。

4.1 施泰因梅茨简介及其论文概况

施泰因梅茨[19-21]（见图 5），1865 年 4 月 9 日出生于德国布雷斯劳，1923 年 10 月 26 日病逝于美国纽约州斯克内克塔迪。他是一位杰出的数学家和电学家，对交流理论的发展作出了巨大贡献，主要体现为以下三大成就：提出磁滞定律、提出计算交流电路的相量法、理论探讨电瞬变现象。

在这里插入图片描述

图 5 美国 1983 年发行的纪念施泰因梅茨 (1865-1923 年)的邮票(图片取自文献[22,23])
Fig.5 The stamp honoring the contributions of Charles Steinmetz (1865-1923) issued by U. S. in 1983 (source of image: [22,23])

施泰因梅茨的论文（见文献[3]）在芝加哥国际电气会议上宣读，随后刊登在 1894 年由美国电机工程师学会出版的《1893 年芝加哥国际电气会议论文集》上，全文共 42 页。

论文在复阻抗的基础上，将正弦电压和正弦电流用复数的代数形式表示，首次建立了复数形式的欧姆定律和交流电路的基尔霍夫定律，并给出这两个定律在交流分析和计算中的应用。文中所提出的相量法改变了计算交流电路的方式，将微分(积分)方程运算转化为代数运算，大大简化了交流电路的计算。应用该方法，电气工程师可以事先估计系统的运行情况，而无需耗资建造无把握的系统，从而降低了电力系统的建造成本。正是由于相量法的提出，电气工程学科最终从物理学中分离出来，成为一个单独的学科[24]。

4.2 成文背景

文献[3]的成文背景主要包括前人的影响以及施泰因梅茨的求学和工作经历。

由于文献[3]未标注任何参考文献，所以我们很难确切判定施泰因梅茨受哪些论著的影响才提出相量法。例如，施泰因梅茨显然是从“阻抗”一文中得知了“复阻抗”，但他在文献[3]中未引用肯涅利的这篇论文，也未提及肯涅利在复阻抗方面的研究工作。施泰因梅茨以前主要从事数学研究，他看过的数学论著应该都用 $i$ 表示 $−1\sqrt{-1}$ ，但在文献[3]中，他用 $j$ 表示 $−1\sqrt{-1}$ 。据此我们推断，他可能看过美国康奈尔大学的物理学教授贝代尔(F. Bedell, 1868-1958 年)和克雷尔(A. C. Crehore, 1868-1958 年)于 1892 年发表的论文“在外加电动势下包含电阻、自感和电容的电路中电流的一般解的推导和讨论”[25]，该文为了避免与电工学科中表示电流的 $i$ 混淆使用了 $j$ 表示虚数单位 $−1\sqrt{-1}$ 。

施泰因梅茨于 1883 年进入德国布雷斯劳大学读本科，随后选择攻读“综合几何”这一方向的博士学位[8]，其博士论文题目为“由 $n$ 阶平面的三维线性系统所确定空间的自我相互对应”[26]。1888 年，当他刚完成博士学位论文时，却得知自己因从事社会主义事业的政治活动将被捕，于是被迫逃往瑞士苏黎世，因此未获得博士学位。后来，他在苏黎世理工学院学习，并从事机械工程研究。1889 年迁居美国，在纽约州扬克斯市艾克迈尔(R. Eickemeyer, 1831-1895 年)的公司工作，1893 年通用电气公司收购了该公司，并雇用了施泰因梅茨。19 世纪 90 年代早期，通用电气公司和威斯汀豪斯电气公司共同竞标“尼亚加拉瀑布发电和配电”项目，当时通用电气公司提交了一个三相系统的设计方案，但项目委员会的首席顾问福布斯(G. Forbes, 1849-1936 年)批评该系统太复杂，他指出：“该系统不能够在三相间保持平衡，且由于没有像威斯汀豪斯电气公司提交的两相系统设计方案那样在相间进行分离，所以该三相系统难以对故障进行定位。”[27]施泰因梅茨是通用电气公司交流方面的专家，因此公司领导安排他解决这一问题。施泰因梅茨的数学和电学理论功底深厚，在读了“阻抗”一文后，从中察觉到一种计算交流电路的新方法，该方法就是相量法。他使用此方法对三相系统进行分析，撰写了文献[3]，并将其在芝加哥国际电气会议上宣读，指出可以使用复数分析计算并避免三相间的不平衡条件[27]。

4.3 论文内容

文献[3]共三部分。

4.3.1 第一部分：引言

这部分一开始就分析了相量法的特点：
(1) 相量法与以前计算交流现象的方法有本质的区别，它用一个复数表示交流电，因而从交流现象的计算中完全消除了“时间”这一独立变量。
(2) 相量法将交流计算问题简化为初等代数问题。此前必须处理关于时间的周期函数，而现在只需对复数进行加、减等运算。

施泰因梅茨接着介绍了图形法，指出因图形法计算量比较大，故可用直角坐标 $a$ 和 $b$ 表示正弦波。而为了区别其水平和垂直分量，他说可在其中一种分量前加一个符号 $j$ ，例如可用 $a + jb$ 表示正弦波，其中 $a$ 、 $b$ 分别为该波的水平和垂直分量。他强调这个 $j$ 只是一个标记，没有任何数值含义。但在计算比正弦波 $a + jb$ 滞后 90°的正弦波时，需要求 $j^2$ 的值，他又通过 $j^{2}=-1$ 定义 $j=−1j=\sqrt{-1}$ ，这样就可用复数 $a + jb$ 表示正弦波。

在此基础上，施泰因梅茨给出包含电阻、电感和电容的电路的阻抗表达式。若电阻为 $r$ ，感抗为 $\pi N L$ ，容抗为 $\pi N K)$ ，其中 $N$ （现用 $f$ ）为交流电频率， $L$ 为自感， $K$ （现用 $C$ ）为电容，则电路的阻抗为 $Z = r - j (s - k)$ （现在电路教材中阻抗为 $Z = r + j (s - k)$ ，造成符号差异的原因是施泰因梅茨定义的矢量旋转方向与现在相反）。

在“引言”的最后，施泰因梅茨介绍了复数的四则运算并给出使用复数代数形式表示同频率正弦量时相位差的计算公式。

4.3.2 第二部分：复数形式的欧姆定律

施泰因梅茨基于阻抗函数，使用复数分析交流电路，建立了复数形式的欧姆定律，并指出（见图 6）：“现在我们建立复数形式的欧姆定律 $E = I Z$ 作为交流电的基本定律。我们可以简单应用欧姆定律 (就像在直流电路中那样，但要注意 $E$ ， $I$ ， $Z$ 是复数)分析和计算任何包含电阻、电感或电容(这些元件以任意方式连接)的交流电路或电路网络。”

在这里插入图片描述

图 6 施泰因梅茨建立复数形式欧姆定律的内容(取自文献[3])
Fig.6 Ohm’s laws in complex form established by Steinmetz in [3]

4.3.3 第三部分：相量法在电力设备和电力系统中的应用

这部分举例说明了相量法在 $R L C$ 电路、变压器和多相传输线中的应用。在“多相传输线”部分，他首次给出交流电路的基尔霍夫定律：沿任一回路， $∑E=0\sum E=0$ ，即所有支路电压的代数和等于零；对任一结点， $∑I=0\sum I=0$ ，即所有流出结点的支路电流的代数和等于零。

5 相量法的提出给予人们的认识

(1) 科学发现不是某个人在某个特定时间的一个单独行为，往往是多人研究的结果。

(2) 工程技术中出现的问题可以促进理论的发展，理论反过来又可以促进工业技术的发展。

6 结论

(1) 亥维赛提出“阻抗”术语，并给出传输线阻抗的定义。

(2) 肯涅利基于阻抗三角形使用复数分析交流电路，在阻抗和复数之间建立了一种对应关系，并提出交流电路的欧姆定律。

(3) 施泰因梅茨将正弦电压和正弦电流用复数的代数形式表示，建立了复数形式的欧姆定律，给出了交流电路的基尔霍夫定律，提出了计算交流电路的相量法。

(4) 阻抗概念的提出使得可以综合考虑交流线路中电阻、电感与电容三个参数的作用；使用复数表示阻抗可以按照直流电路的规则来处理交流电路；使用复数表示正弦电压和正弦电流可将正弦交流电路的计算简化为复数运算。

参考文献

[1] Heaviside O. Electrical papers (vol.2) [M]. London: Macmillan, 1892.

[2] Kennelly A E. Impedance [J]. Transactions of the AIEE, 1893, 10: 175-232.

[3] Steinmetz C P. Complex quantities and their use in electrical engineering [C]. Proceedings of the International Electrical Congress, Chicago: 1893. New York: American Institute of Electrical Engineers, 1894: 33-74.

[4] Wikipedia. Oliver Heaviside [EB/OL]. [2010-06-11]. https://en.wikipedia.org/wiki/Heaviside.

[5] 中国大百科全书总编委会，物理学编委会. 中国大百科全书·物理学 [M]. 北京：中国大百科全书出版社，1987.

[6] Baber R L. Comparison of electrical “engineering” of Heaviside’s times and software “engineering” of our times [J]. IEEE Annals of the History of Computing, 1997, 19(4): 5-17.

[7] 祖贝 R. 英德法俄汉物理学词典：A-M [M]. 物理学词典翻译组，译. 北京：原子能出版社，1980.

[8] Kline R R. Steinmetz: engineer and socialist [M]. Baltimore, London: The Johns Hopkins University Press, 1992.

[9] Heaviside O. Electrical papers (vol.1) [M]. London: Macmillan, 1892.

[10] Heaviside O. On resistance and conductance operators, and their derivatives, inductance and permittance, especially in connexion with electric and magnetic energy [J]. Philosophical Magazine, 1887, 24(151): 479-502.

[11] Nahin P J. Oliver Heaviside: the life, work, and times of an electrical genius of the Victorian age [M]. Baltimore, MD: The Johns Hopkins University Press, 2002.

[12] IEEE Global History Network. Arthur E. Kennelly [EB/OL]. [2010-06-20]. https://ieeeghn.org/wiki/index.php/Arthur_E._Kennelly.

[13] Brittain J E. Electrical engineering hall of fame: Arthur E. Kennelly [J]. Proceedings of the IEEE, 2006, 94(9): 1772-1775.

[14] Gillispie C C. Dictionary of scientific biography (vol.7) [M]. New York: Scribner, 1981.

[15] Arthur E. Kennelly [J]. Proceedings of the Institute of Radio Engineers, 1930, 18(10): 1614.

[16] Fleming J A. The alternate current transformer in theory and practice (vol.1) [M]. 3rd ed. London: The Electrician Printing and Publishing Company, Limited, 1900.

[17] Arthur Edwin Kennelly [EB/OL]. [2010-12-01]. https://www.quotesinscience.com/K/Kennelly_Arthur/Kennelly_Arthur.htm.

[18] Wikipedia. Arthur E. Kennelly [EB/OL]. [2010-06-02]. https://en.wikipedia.org/wiki/Arthur_Edwin_Kennelly.

[19] Wikipedia. Charles Proteus Steinmetz [EB/OL]. [2010-06-21]. https://en.wikipedia.org/wiki/Charles_Proteus_Steinmetz.

[20] Anon. The magnetic force of Charles Proteus Steinmetz [J]. IEEE Power Engineering Review, 1996, 16(9): 7-12.

[21] 不列颠百科全书：国际中文版 [M]. 中国大百科全书出版社，不列颠百科全书编辑部编译. 北京：中国大百科全书出版社，2007.

[22] Philatelic Database. Stamps of the U.S.: 1983 “inventors” stamp issue [EB/OL]. [2011-01-13]. https://www.whitmanbooks.com/Default.aspx?Page=81&ProductID=2055M.

[23] Whitman Publishing. Stamp of honoring the contributions of Steinmetz issued by U.S. [EB/OL]. [2011-01-13]. https://www.whitmanbooks.com/Default.aspx?Page=81&ProductID=2055M.

[24] 高橋雄造. 百万人の電気技術史 [M]. 東京：工業調査会，2006.

[25] Bedell F, Crehore A C. Derivation and discussion of the general solution for the current flowing in a circuit containing resistance, self-induction and capacity, with any impressed electromotive force [J]. Transactions of the AIEE, 1892, 9(1): 303-374.

[26] Coleman M. Pioneers of freedom [M]. New York: The Vanguard Press, 1929.

[27] Kline R R. Charles P. Steinmetz and the development of electrical engineering science [D]. Madison, WI: University of Wisconsin-Madison.

作者简介

张亮亮女，1978 年生，博士研究生，讲师，研究方向为中国电气史。
雷银照男，1956 年生，教授，博士生导师，研究方向为电磁场理论及其应用、中国电气史。

“电路、信号与系统”中的相量和频域分析教学方法研究

林凌*，曾周末，栗大超，张宇，刘蓉，杨春梅
天津大学精密仪器与光电子工程学院，天津
Email:linling@tju.edu.cn

收稿日期:2019年10月8日；录用日期:2019年10月24日；发布日期:2019年10月31日

摘要

在“电路基础理论”和“信号与系统”两门课程中，基于相量法的电路正弦稳态分析与系统频域分析都是十分重要的内容，两者之间存在着深刻的内在联系，然而初学者不易把握。本文在剖析相量法和频域法的本质、异同和教学过程所遇到问题的基础上，提出了一个全新的授课思路，希望能改进“电路、信号与系统”课程的教学时效。

关键词

电路；信号与系统；相量法；频域分析

文章引用: 林凌, 曾周末, 栗大超, 张宇, 刘蓉, 杨春梅. “电路、信号与系统”中的相量和频域分析教学方法研究[J]. 创新教育研究, 2019, 7(5): 679-685. DOI: 10.12677/ces.2019.75115

1 引言

对于高等学校电子信息类专业来说，“电路基础理论”和“信号与系统”是两门十分重要的学科基础课程。其中，基于相量法的电路正弦稳态分析和系统频域分析都是十分重要的内容，两者之间有着深刻的内在联系。然而，多年的教学经验表明，学生不易将这两部分内容联系起来，比如，不能把“信号与系统”中电路的频域模型、频响特性与“电路基础理论”中的相量模型、网络函数联系起来。在“信号与系统”中应用频域分析方法求解分析电路稳态问题时，往往机械运用傅氏变换和逆变换方法得到输出信号，不能从本质上把握系统频响特性的物理意义，难以提高实际分析解决电路问题的能力。另一方面，将“电路基础理论”和“信号与系统”两门课程合并成“电路、信号与系统”课程时也需要深入研究教学方法。

本文在剖析传统“电路基础理论”课程中的相量法和“信号与系统”中频域分析方法的本质、异同和教学中遇到的问题的基础上，针对“电路、信号与系统”课程提出一种全新的授课思路，希望让学生在相对比较少的课时情况下，掌握电路稳态问题的分析方法，理解系统频响特性的实际意义。

2 传统电路理论课程中相量法

传统的电路基础理论课程一般首先在纯电阻电路的环境里介绍电路的基本规律、基本定理和分析方法。有的教材[1]把这部分内容称为“直流电路”。但笔者更愿意采用“电阻电路”这一提法。纯电阻电路本质上是一个“即时、无记忆”系统，描述其输入、输出关系的数学模型是代数方程(组)。在这种“零阶”系统环境下，讨论电路的基本规律、定理和分析方法都十分方便且容易被接受。事实上，不仅仅是直流激励，交流信号激励下电阻电路的分析方法都是一样的。因为，对于一个“零阶”线性系统，输入、输出或者说各处信号之间的关系是一个“比例”关系。另一方面，所谓直流电路是指激励为直流信号的电路，原则上电路中除了电阻，还可以有电容、电感等“记忆”元件。只是，在直流信号激励下，电容表现为断路(电阻无穷大)、电感表现为短路(电阻为零)，因此输入、输出或者说各处信号之间依然为“比例”关系。所以，纯电阻电路和直流电路可以归类为“静态电路”，其输入、输出信号之间的关系是一个取决电路结构和参数的“比例”关系。

含有电感、电容等“记忆”元件，在非直流信号激励下的电路便被称为“动态电路”。动态电路在数学模型上表现为一阶以上的微分方程(组)；稳定的动态电路在功率信号的激励下将产生瞬态响应和稳态响应。由于直接由电路微分方程求解其稳态响应是个繁琐的过程，于是便有了基于相量法的正弦稳态分析。一般地，电路基础理论的教材都是从正弦信号的三要素，即幅值、频率、相角开始引入正弦信号的相量表示，通过讨论电阻、电感和电容端电压与其中电流的关系引出感抗和容抗，介绍相量形式的 KCL 和 KVL，进而给出电路复阻抗以及电路的相量模型。相量法大大方便了动态电路的稳态分析，但传统相量法的教学过程琐碎、繁杂，需要消耗较多的课时资源、且难以形成更具有普遍意义的理论方法。

3 信号与系统课程中的频域分析方法

“信号与系统”对信号和系统给出了更一般化的描述，信号的时域、频域与 S 域分解，系统的时域、频域与 S 域分析，依次展开，层层推进，概念丰富、逻辑清晰、理论完整，无疑在更高的层面上提供了分析包括电路系统在内的动态系统的理论方法。然而，多年的教学实践中注意到，学生对于把握信号系统框架中时域、频域与 S 域三类不同分析方法的本质与内在关系感到困难，比较容易停留在纯粹的数学变换层面；并且对“信号与系统”和“电路基础理论”中相关联的内容，如系统稳态响应分析以及系统频响特性，与“电路基础理论”中正弦稳态分析部分的关系认识不到位，导致花费了大量的课堂资源，却没有收到应有的教学效果。例如，已知系统频率响应函数 $\omega)$ 如图 1 所示，当 $\cos (5 t)+4 \cos (10 t)$ 时，求系统响应。

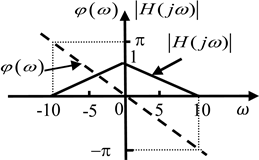
在这里插入图片描述

图 1 某系统幅频和相频特性
Figure 1. Amplitude and phase frequency characteristics of a system

有学生采用傅里叶级数法。首先写出
$\cos (5 t)+4 \cos (10 t)=\sum_{n=-2}^{2} 2 e^{j n 5 t}$
所以 $Fn={2,n=0,±1,±20,其余F_{n}= \begin{cases}2, & n=0, \pm 1, \pm 2 \\ 0, & 其余 \end{cases}$ ，再由 $Yn=H(jω)∣ω=5nFnY_{n}=H(j \omega)|_{\omega=5 n} F_{n}$ ，得
$y(t)=∑n=−22Ynejn5t=0+e−j(5t−90∘)+2+ej(5t−90∘)+0=2+2cos⁡(5t−90∘)\begin{aligned} y(t) & =\sum_{n=-2}^{2} Y_{n} e^{j n 5 t} \\ & =0+e^{-j\left(5 t-90^{\circ}\right)}+2+e^{j\left(5 t-90^{\circ}\right)}+0 \\ & =2+2 \cos \left(5 t-90^{\circ}\right) \end{aligned}$

也有学生采用傅里叶变换法。因为， $\omega)=4 \pi \sum\limits_{n=-2}^{2} \delta(\omega-5 n)$ ，通过 $\omega)=H(j \omega) F(j \omega)$ ，可得

$\omega)=4 \pi\left[0.5 e^{j 90^{\circ}} \delta(\omega+5)+\delta(\omega)+0.5 e^{-j 90^{\circ}} \delta(\omega-5)\right]$

再取傅立叶逆变换得

$y(t)=e−j(5t−90∘)+2+ej(5t−90∘)=2+2cos⁡(5t−90∘)y(t)=e^{-j\left(5 t-90^{\circ}\right)}+2+e^{j\left(5 t-90^{\circ}\right)}=2+2 \cos \left(5 t-90^{\circ}\right)$

以上两种方法都具备数学上的严谨和完美，却未能凸显系统频率响应函数 $\omega)$ 的物理意义。
事实上，从图 1 可以清楚地看到系统的关键频率特性：

直流增益为 $1\boldsymbol{1}$ （对应 $ω=0\omega=0$ 时）；
角频率 $ω=5rad/s\boldsymbol{\omega=5\ \text{rad/s}}$ 处，增益为 $0.5\boldsymbol{0.5}$ ，相移为 $−0.5πrad\boldsymbol{-0.5\pi\ \text{rad}}$ （即 $−90∘-90^\circ$ ）；
角频率 $ω=10rad/s\boldsymbol{\omega=10\ \text{rad/s}}$ 处，增益为 $0\boldsymbol{0}$ 。

因此，结合输入信号特性，可直接得到系统的输出响应为：
$y(t)=2+2cos⁡(5t−90∘)\boldsymbol{y(t) = 2 + 2\cos(5t - 90^\circ)}$

我们把这种通过直接读取幅频、相频特性求解响应的方法称为幅频相频法。相较傅里叶级数法和傅里叶变换法，幅频相频法更清晰地反映了系统频率响应特性的本质。

“信号与系统”作为一门独立的课程是在“电路基础理论”之后[2]，其中系统频域分析部分与“电路基础理论”中的相量法以及相关的阻抗、网络函数等概念之间的有着深刻的内在联系。然而教学中发现，能够把这两个方法联系起来灵活应用的学生不多。例如，如图 2 所示周期方波电压源 $u_{s}(t)$ 作用于 RL 电路，试求电流 $i (t)$ 的前五次谐波。

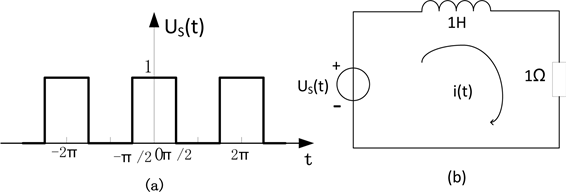
在这里插入图片描述

图 2 周期方波信号作用于 RL 电路
Figure 2. Periodic square wave signal acts on the RL circuit

部分学生的解题过程如下:

求出 $u_{s}(t)$ 的前五次谐波表达式:
$us(t)∣0,−,5=12+2πcos⁡(t)−23πcos⁡(3t)+25πcos⁡(5t)\left.u_{s}(t)\right|_{0,-, 5}=\frac{1}{2}+\frac{2}{\pi} \cos (t)-\frac{2}{3 \pi} \cos (3 t)+\frac{2}{5 \pi} \cos (5 t)$
列写微分方程 $i'(t)+i(t)=u_{s}(t)$
设 $i (t)$ 的前五次谐波为

$C_{0}+C_{1} \cos (t)+C_{2} \sin (t)+C_{3} \cos (3 t)+C_{4} \sin (3 t)+C_{5} \cos (5 t)+C_{6} \sin (5 t)$

代入微分方程求得 7 个待定系数;
最后得到 $i (t)$ 的前五次谐波为

$12+1πcos⁡(t)+1πsin⁡(t)−115πcos⁡(3t)−15πsin⁡(3t)+165πcos⁡(5t)+113πsin⁡(5t)\frac{1}{2}+\frac{1}{\pi} \cos (t)+\frac{1}{\pi} \sin (t)-\frac{1}{15 \pi} \cos (3 t)-\frac{1}{5 \pi} \sin (3 t)+\frac{1}{65 \pi} \cos (5 t)+\frac{1}{13 \pi} \sin (5 t)$

以上过程计算繁琐。若采用幅频相频法则会很简洁，即首先写出系统的频率响应函数
$\omega)=\frac{I(j \omega)}{U_{s}(j \omega)}=\frac{1}{1+j \omega}$
然后分别计算其在 $ω=0,1,3,5\omega=0,1,3,5$ 时的幅值与相角，便可方便地求出 $i (t)$ 的前五次谐波。事实上，以上方法与“电路基础理论”中的相量法在本质上是一致的，关键是如何让学生认识到。

4 电路、信号与系统课程中的系统稳态分析

以上分别分析了基于相量法和频域分析的系统稳态分析方法，以及目前教学实践中存在的问题。下面讨论在“电路、信号与系统”课程中，如何通过一个全新的授课思路，让学生在相对比较少的课时条件下，真正掌握电路稳态问题的分析方法，理解系统频响特性的实际意义。

“电路基础理论”与“信号与系统”两门课程的结合点在于动态电路的分析方法。笔者之前提出了“电路、信号与系统”课程的总体组织框架[3]，即电路篇、信号篇和系统篇。基本思想是：

在电路篇中，在电阻电路的环境下介绍电路所特有的基本规律、定理和分析方法；在动态电路部分，先介绍基本的动态元件（如电感、电容等）的伏安关系，动态电路微分方程的列写以及响应的构成，强调动态电路所具有的动态响应和稳态响应过程。电路正弦稳态分析则从电路篇中移出，合并到系统篇中的系统稳态分析部分，在频域分析方法之后引出。
在信号篇里，以线性叠加定理为切入点，系统介绍信号的时域、频域以及 $s$ 域的分解。在强调积分、傅氏和拉氏三大变换的物理意义的同时，为解决动态系统分析提供必要的数学工具。
在系统篇里，打破时域、频域以及 $s$ 域分析的传统框架，将系统篇分为系统动态分析和稳态分析两个部分，灵活应用数学工具为系统分析服务。例如，在系统动态分析部分，直接把时域和 $s$ 域方法打通，引入电路的 $s$ 域模型，强调指出，在 $s$ 域模型下，之前电路篇中的电阻电路的理论、分析方法可以完全移植过来，从而方便地解决动态电路的动态分析。在动态过程分析中，强调系统过渡过程和稳态响应的概念，为系统稳态分析做好铺垫。

系统稳态分析的重要概念是系统的频率响应特性，其次是明确所谓系统的稳态响应本质上是稳定系统在功率信号激励下的响应，也就是系统对正弦信号的响应的合成。为防止学生落入纯数学推演的陷阱，将系统在正弦信号激励下的响应与系统频率特性的关系直接以“定理”的形式给出，然后通过三种途径加以证明。

定理：频率响应特性为 $\omega)$ 的系统在 $\cos (\omega_{0} t+\varphi_{0})$ 激励下的稳态响应为
$y(t)=A∣H(jω0)∣cos⁡[ω0t+φ0+φ(ω0)]y(t)=A\left|H\left(j \omega_{0}\right)\right| \cos \left[\omega_{0} t+\varphi_{0}+\varphi\left(\omega_{0}\right)\right]$

证明一：设系统的输入为 $f1(t)=Aej(ω0t+φ0)f_{1}(t)=A e^{j(\omega_{0} t+\varphi_{0})}$ 、冲激响应为 $h (t)$ ，则系统的输出为
$y1(t)=f1(t)∗h(t)=∫−∞+∞Aej[ω0(t−τ)+φ0]h(τ)dτ=Aej(ω0t+φ0)∫−∞+∞Ae−jω0τh(τ)dτ=Aej(ω0t+φ0)H(jω0)=A∣H(jω0)∣ej(ω0t+φ0)ejφ(ω0)=A∣H(jω0)∣ej[ω0t+φ0+φ(ω0)]\begin{aligned} y_{1}(t) & =f_{1}(t) * h(t)=\int_{-\infty}^{+\infty} A e^{j\left[\omega_{0}(t-\tau)+\varphi_{0}\right]} h(\tau) d \tau \\ & =A e^{j\left(\omega_{0} t+\varphi_{0}\right)} \int_{-\infty}^{+\infty} A e^{-j \omega_{0} \tau} h(\tau) d \tau \\ & =A e^{j\left(\omega_{0} t+\varphi_{0}\right)} H\left(j \omega_{0}\right) \\ & =A\left|H\left(j \omega_{0}\right)\right| e^{j\left(\omega_{0} t+\varphi_{0}\right)} e^{j \varphi\left(\omega_{0}\right)} \\ & =A\left|H\left(j \omega_{0}\right)\right| e^{j\left[\omega_{0} t+\varphi_{0}+\varphi\left(\omega_{0}\right)\right]} \end{aligned}$
由于 $\cos (\omega_{0} t+\varphi_{0})$ 是 $f1(t)=Aej(ω0t+φ0)f_{1}(t)=A e^{j(\omega_{0} t+\varphi_{0})}$ 的实部，所以系统的输出 $y (t)$ 也是 $y_1(t)$ 的实部，即 $\omega_{0})| \cos [\omega_{0} t+\varphi_{0}+\varphi(\omega_{0})]$ 。

证明二：设系统的输入为 $f1(t)=cos⁡(ω0t)ε(t)f_{1}(t) = \cos (\omega_{0} t) \varepsilon(t)$ ，传递函数为 $H (s)$ 。则系统输出 $y_{1}(t)$ 的拉氏变换为：
$Y1(s)=ss2+ω02H(s)=Y1h(s)+121s−jω0H(jω0)+121s+jω0H(−jω0)Y_{1}(s) = \frac{s}{s^{2} + \omega_{0}^{2}} H(s) = Y_{1 h}(s) + \frac{1}{2} \frac{1}{s - j \omega_{0}} H\left(j \omega_{0}\right) + \frac{1}{2} \frac{1}{s + j \omega_{0}} H\left(-j \omega_{0}\right)$
其中， $Y_{1 h}(s)$ 对应输出中的暂态响应部分的拉氏变换，其余项对应稳态响应：
$y1ss(t)=∣H(jω0)∣cos⁡[ω0t+φ(ω0)]y_{1 s s}(t) = |H(j \omega_{0})| \cos [\omega_{0} t + \varphi(\omega_{0})]$

同理，当输入为 $f2(t)=sin⁡(ω0t)ε(t)f_{2}(t) = \sin (\omega_{0} t) \varepsilon(t)$ 时，稳态响应为：
$y2ss(t)=∣H(jω0)∣sin⁡[ω0t+φ(ω0)]y_{2 s s}(t) = |H(j \omega_{0})| \sin [\omega_{0} t + \varphi(\omega_{0})]$

因此，当输入为 $\cos (\omega_{0} t + \varphi_{0}) \varepsilon(t)$ 时，稳态响应为：
$yss(t)=A∣H(jω0)∣cos⁡[ω0t+φ0+φ(ω0)]y_{s s}(t) = A |H(j \omega_{0})| \cos [\omega_{0} t + \varphi_{0} + \varphi(\omega_{0})]$

证明三：设系统的输入为 $f1(t)=cos⁡(ω0t)f_{1}(t) = \cos (\omega_{0} t)$ ，频响特性为 $\omega)$ 。则系统输出 $y_{1}(t)$ 的傅氏变换为：
$Y1(jω)=H(jω)π[δ(ω−ω0)+δ(ω+ω0)]=π[H(jω0)δ(ω−ω0)+H(−jω0)δ(ω+ω0)]\begin{aligned} Y_{1}(j \omega) & = H(j \omega) \pi \left[ \delta(\omega - \omega_{0}) + \delta(\omega + \omega_{0}) \right] \\ & = \pi \left[ H(j \omega_{0}) \delta(\omega - \omega_{0}) + H(-j \omega_{0}) \delta(\omega + \omega_{0}) \right] \end{aligned}$
所以，时域中的输出为：
$y1(t)=∣H(jω0)∣cos⁡[ω0t+φ(ω0)]y_{1}(t) = \left| H(j \omega_{0}) \right| \cos \left[ \omega_{0} t + \varphi(\omega_{0}) \right]$

同理，当输入为 $f2(t)=sin⁡(ω0t)f_{2}(t) = \sin (\omega_{0} t)$ 时，响应为：
$y2(t)=∣H(jω0)∣sin⁡[ω0t+φ(ω0)]y_{2}(t) = \left| H(j \omega_{0}) \right| \sin \left[ \omega_{0} t + \varphi(\omega_{0}) \right]$

故，当输入为 $\cos (\omega_{0} t + \varphi_{0})$ 时，响应为：
$\left| H(j \omega_{0}) \right| \cos \left[ \omega_{0} t + \varphi_{0} + \varphi(\omega_{0}) \right]$

从以上证明过程可以看到，正是由于在信号篇中解决了所有相关的数学问题，才使得在系统篇中可以方便、灵活地加以应用。这也有助于学生体会时域、频域和 $s$ 域的本质及其相互之间的联系。

在解决了一般线性系统的稳态响应后，再回头看电路的正弦稳态分析方法。首先，在动态电路的时域模型的基础上引入电路的频域模型，强调指出，之前电路篇中的电路理论、分析方法同样可以完全移植到频域模型中来。同时，考虑到相量法在很多教材和文献中都会出现，有必要对读者和学生进行说明。而且，在讲完频域方法后，可以以一个全新的角度，更加简洁地引入电路的相量模型。

从上面的证明一可以看到，由于 $\cos (\omega_{0} t + \varphi_{0})$ 是 $e^{j(\omega_{0} t + \varphi_{0})}$ 的实部，我们可以记输入、输出的相量形式分别为：
$F˙=Aej(ω0t+φ0),Y˙=∣H(jω0)∣Aej[ω0t+φ0+φ(ω0)].\begin{aligned} \dot{F} &= A e^{j(\omega_{0} t + \varphi_{0})}, \\ \dot{Y} &= |H(j \omega_{0})| A e^{j[\omega_{0} t + \varphi_{0} + \varphi(\omega_{0})]}. \end{aligned}$
这样就可以写出正弦信号激励下系统输入、输出的相量形式的表达式：
$Y˙=F˙H(jω0).\dot{Y} = \dot{F} H(j \omega_{0}).$

回到传统电路理论中的正弦稳态分析。正弦与相量形式的电流、电压表达式为：
$i(t)=2Icos⁡(ω0t+φi0),u(t)=2Ucos⁡(ω0t+φu0),\begin{aligned} i(t) &= \sqrt{2} I \cos (\omega_{0} t + \varphi_{i 0}), \\ u(t) &= \sqrt{2} U \cos (\omega_{0} t + \varphi_{u 0}), \end{aligned}$
和
$I˙=Iejφi0=I∠φi0,U˙=Uejφu0=U∠φu0.\begin{aligned} \dot{I} &= I e^{j \varphi_{i 0}} = I \angle \varphi_{i 0}, \\ \dot{U} &= U e^{j \varphi_{u 0}} = U \angle \varphi_{u 0}. \end{aligned}$

对比两种相量记法，在电路理论中，相量的模是其有效值，相角只记初相角而略去了角频率。之前电阻电路中的电路理论、分析方法同样可以完全移植到动态电路的相量模型中来。两种相量记法在本质上是一致的，都可以方便地表达系统在正弦信号激励下的稳态响应。

基于以上对系统频域分析方法和电路理论中相量法内在关系的深入剖析，在最近的两个教学周期里，我们实施了一个全新的教学方法，即略去传统电路理论中的正弦稳态分析部分，在系统频域分析理论下讲清系统在正弦激励下的响应之后，引入一般意义的相量表达，接着介绍电路理论中的相量法。应用这种方法，只需增加一个学时便可完成相量法的讲授。相较传统讲授方法所需的 5 个学时，显著地减少了授课学时；同时我们发现这样的讲授方法让学生们进一步看清了一般系统频域分析与电路系统相量分析之间的内在联系并加以灵活应用。

5 总结

本文剖析了电路基础理论中基于相量法的正弦稳态分析和信号系统中的频域分析方法，针对“电路、信号与系统”课程，提出一个全新的授课思路。两个周期的教学实践表明，应用这个授课思路，能够大幅减少授课学时，同时又让学生认识到一般系统频域分析与电路系统相量分析之间的联系并加以灵活应用，从而改进了相关内容的教学效果、提高了教学时效。

“电路基础理论”和“信号与系统”两门课程连接点在于动态电路的分析。在多数“电路基础理论”教材中，是以分析对象、分析任务为“导向”，在需要的地方引入相应的数学知识，使学习者往往因为零散出现的数学问题而感到困惑；而“信号与系统”更偏重于理论方法的系统完整性，使得一些学习者不自觉地陷入数学推演里，从而忽视了理论的工程背景及其实际应用。因此，当把“电路基础理论”和“信号与系统”两门课程整合到一起时，应该在一个更高的层面审视两门课程的理论体系，寻求更加合理、更加高效的课程组织体系和教学方法，让学生在更少的课堂学时资源的情况下，更好地掌握电路与信号系统的核心理论并能够灵活地应用于解决实际问题。本文提出的关于频域分析和相量法的教学方法便是研究两门课程内在关系的一个实例。

参考文献

[1] (美)亚历山大. 电路基础(英文版)[M]. 第五版. 北京: 机械工业出版社, 2013.
[2] 郑君里, 谷源涛. 信号与系统课程历史变革与进展[J]. 电气电子教学学报, 2012, 34(2): 1-6.
[3] 林凌, 曾周末, 栗大超, 张宇, 刘蓉. “电路、信号与系统”课程内容组织体系[J]. 电气电子教学学报, 2018, 40(5): 52-56.

电路分析 | Phasor Analysis（篇 2）-CSDN博客
https://blog.csdn.net/u013669912/article/details/154394138

via:

相量法历史上的三篇经典文献张亮亮雷银照 - 2011
https://dgjsxb.ces-transaction.com/CN/abstract/abstract21.shtml
“电路、信号与系统”中的相量和频域分析教学方法研究 2019
https://www.hanspub.org/journal/paperinformation?paperid=32782

查看全文

http://www.dtcms.com/a/568771.html