2025年SEVC SCI2区，具有互补和集成变异策略的双阶段自适应差分进化算法用于求解全局优化问题，深度解析+性能实测

—

1.摘要

差分进化算法（DE）由于其卓越的性能，广泛应用于解决各类实际优化问题。然而，该算法存在一些挑战，如对参数的高度敏感性以及优化能力对特定应用的偏向。本文提出了DE变体——LSHADE-Code，旨在解决全局优化问题，该方法引入了一种新颖的均值计算模式，基于莱默均值，并采用线性插值技术，确保在参数调整时平稳过渡，从而有效避免了依赖加权莱默均值的自适应方案中常见的过早收敛问题。LSHADE-Code还提出了一种创新变异策略，通过对称互补机制和高斯概率分布的特性，提升了搜索效率，增强了进化阶段的探索能力。同时，结合两种其他变异策略，形成复合变异方法，使得算法能够根据个体情况动态选择最合适的策略。此外，LSHADE-Code强化了LSHADE算法的种群减少机制，促进了进化后期种群规模的快速收缩，从而提高了局部探索能力。

2.具有互补和集成变异策略的双阶段自适应差分进化算法

互补变异策略

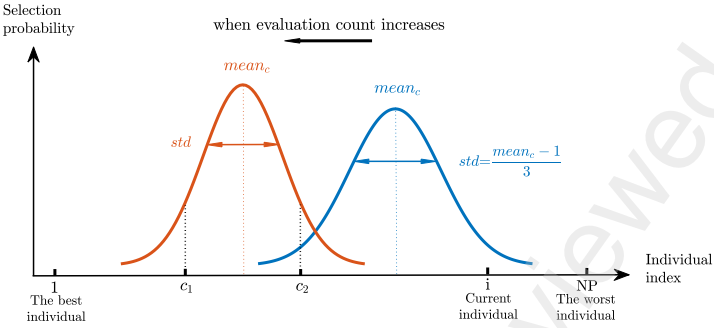
论文引入了一种新的变异策略——DE/current-to-crand/1，结合了对称互补机制和高斯概率分布，以平衡不同进化阶段的局部和全局探索。在变异开始前，个体根据适应度值升序排序。对于每个个体$X_i$，通过基于高斯分布的公式计算一个索引，使得$X_{c_1}$更可能与个体$X_i$接近，而不是最优个体，特别是在进化过程推进时，$mea{n}_c$的计算公式随评估次数的增加，确保更倾向选择最优个体，而避免选择较差个体。

个体更新：
$$V_l^g=X_l^g+F\times \left(X_{c1}^g-X_l^g\right)+F\times \left(X_{c2}^g-X_{r1}^g\right)$$

集成变异策略

为了应对不同优化问题的多样需求，LSHADE-Code采用了一种复合变异策略，结合了三种变异策略，并根据每种策略在进化过程中的表现进行动态调整。DE/current-to-pbest/1,DE/current-to-crand/1，DE/scaled best/1。

在每一代进化中，个体根据每种策略的选择概率来决定采用哪种变异策略。进化后，通过分析成功个体的目标函数值减少情况，评估各策略的有效性，并根据表现调整选择概率，将更有效的策略赋予更高的选择概率。

$$p{b}_j^{g+1}=\frac{su{s}_j^g}{{\sum }_{j=1}^{3}su{s}_j^g}$$

susjg=∑i=1NPmax[0,(f(Xig,j)−f(Uig,j))/f(Xig,j)]j={1,2,3}sus_j^g=\sum_{i=1}^{NP}max[0,(f(X_i^{g,j})-f(U_i^{g,j}))/f(X_i^{g,j})]\quad j=\{1,2,3\} susjg​=i=1∑NP​max[0,(f(Xig,j​)−f(Uig,j​))/f(Xig,j​)]j={1,2,3}

种群缩减方法

论文改进了种群缩减方法以便根据进化进程逐步减少个体数量：
$$N{P}^{g+1}=round\left[N{P}_{min}+\epsilon \times \frac{nfe{s}^g}{ma{x}_{n}fes}\times (N{P}_{ini}-N{P}_{min})\right]$$

3.结果展示

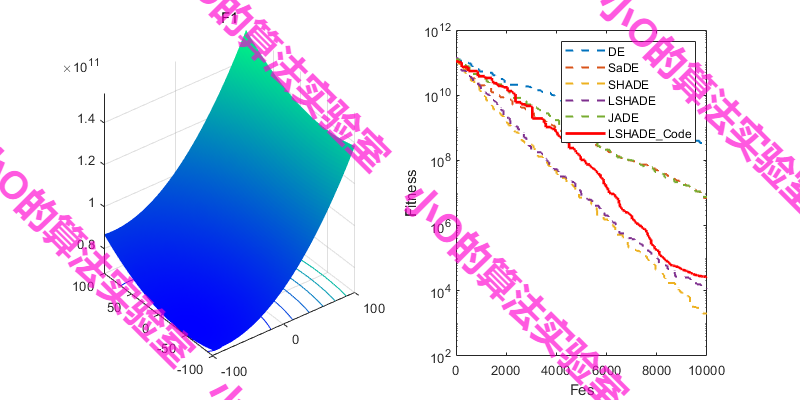
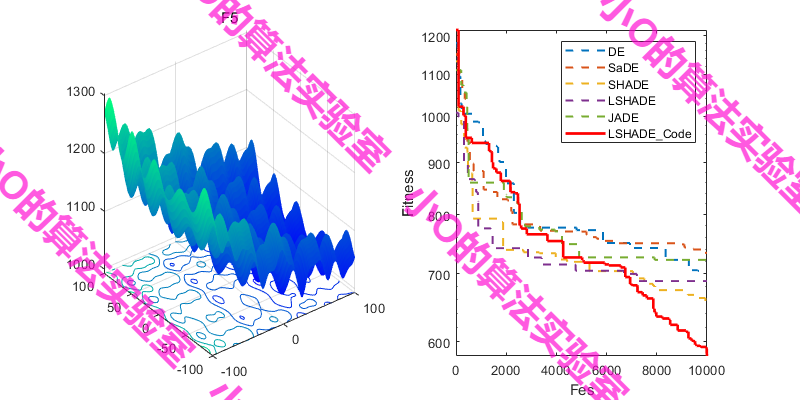
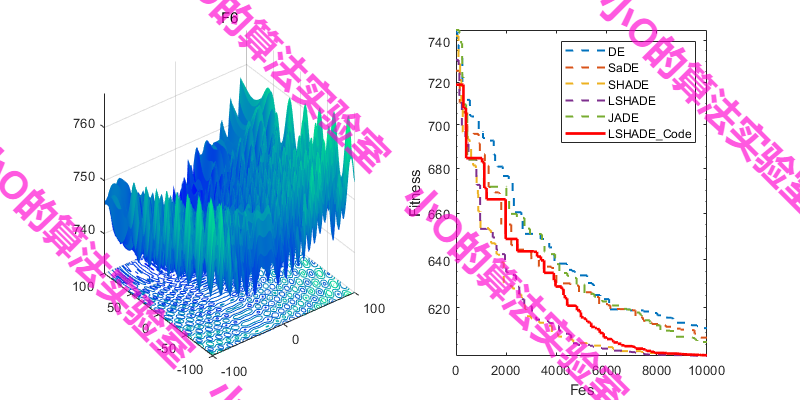
4.参考文献

[1] Chen B, Ouyang H, Li S, et al. Dual-stage self-adaptive differential evolution with complementary and ensemble mutation strategies[J]. Swarm and Evolutionary Computation, 2025, 93: 101855.

5.代码获取

xx

6.算法辅导·应用定制·读者交流

xx