【动态规划：01背包】01背包详解 模板题 优化

背包问题概述

​ 终于到了动态规划的一类很有名的问题，背包问题了！为什么背包问题让人听起来就怕呢，因为它是基于动态规划的，本身动态规划就是千变万化，再加上背包问题的一些限定条件，使得背包问题也是分为很多类不同的问题，如 01背包、完全背包等等。

​ 背包问题 (Knapsack problem) 其实也是⼀种组合优化的 NP完全问题。其问题可以描述为：给定⼀组物品，每种物品都有⾃⼰的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最⾼。

​ 根据物品的个数，分为如下几类：

• 01 背包问题：每个物品只有一个
• 完全背包问题：每个物品有无限多个
• 多重背包问题：每件物品有 $s_i$ 个，即为有限个，介于前两者之间
• 混合背包问题：每个物品会有上面三种情况
• 分组背包问题：物品有 n 组，每组物品里有若干个，每组里最多选一个物品

​ 其中上述分类里面，根据背包是否装满，又分为两类：

• 不一定装满背包
• 背包一定装满

​ 根据限定条件的个数，又分为两类：

• 限定条件只有一个：比如体积 -> 普通的背包问题
• 限定条件有两个：比如体积 + 重量 -> 二维费用背包问题

​ 根据不同的问法，又分为很多类：

• 输出方案
• 求方案总数
• 最优方案
• 方案可行性

​ 其实还有很多分类，但是我们仅需了解即可。

​ 因此，背包问题种类非常繁多，题型非常丰富，难度也是非常难以捉摸。但是，尽管种类非常多，都是从 01 背包问题演化过来的。所以，⼀定要把 01 背包问题学好。

​ 并且在背包问题中，优化是很有必要的，前面的动态规划题目中其实我们没怎么提到优化，那是因为优化的效果不显著，并且前面的题目也是为了让我们能快速的入门动态规划！

​ 而 背包问题就不一样了，其优化的意义很大，不仅仅对时间复杂度有提升，空间复杂度也会有提升，常见的优化方案如下：

• 空间优化：滚动数组
• 单调队列优化
• 贪心优化

​ 下面我们就从最经典的 01 背包问题开始旅程！

01 背包（medium）

DP41 【模板】01背包

你有一个背包，最多能容纳的体积是 V。

现在有 n 个物品，第 i 个物品的体积为 vi，价值为 wi

（1）求这个背包至多能装多大价值的物品？

（2）若背包 恰好装满，求至多能装多大价值的物品？

输入描述：

​ 第一行两个整数 n 和 V，表示物品个数和背包体积。

​ 接下来 n 行，每行两个数 vi 和 wi，表示第 i 个物品的体积和价值。

​ 其中 1 ≤ n, V, vi, wi ≤ 1000

输出描述：

​ 输出有两行，第一行输出第一问的答案，第二行输出第二问的答案，如果无解请输出0。

示例1

输入：3 52 104 51 4
输出：14 9
说明：装第一个和第三个物品时总价值最大，但是装第二个和第三个物品可以使得背包恰好装满且总价值最大。 

示例2

输入：3 812 611 86 8
输出：8 0
说明：装第三个物品时总价值最大但是不满，装满背包无解。

备注：

​ 要求 O(nV) 的时间复杂度，O(V) 空间复杂度

---

1、第一问解题思路

​ 在做背包问题的时候，题目给的实例中的参数对应是什么要搞清楚，并且在背包问题中有几个常见的字符：V 常表示 背包的容量、n 常表示 物品的个数、v 常表示 物品的体积、w 常表示 物品的价值 等等。

​ 背包问题的本质还是动态规划，我们还是能够按照之前的五部曲来一一解析每一步，下面一起来！

状态表示

​ 根据 ”经验 + 题目要求“，我们通过都会以某个位置为结尾然后……的情况来分析，这道题也是如此，题目问这个背包至多能装多大价值的物品，那我们就可以先定义一个状态为 dp[i] 表示从前 i 个物品中选择，在这些选法中能装入背包的最大物品价值。

​ 看似这种状态表示没问题，但是其实这个状态表示不足以推出状态转移方程，因为当我们在推导 dp[i] 的时候，我们 不仅仅要知道当前物品的价值，还要知道背包还能装下多大的物品，显然上面的状态表示并不能体现出来，所以我们可以多加一个维度，提供一个背包体积的状态。

​ 所以最终状态表示为：dp[i][j] 表示从前 i 个物品中选择，并且物品总体积不超过 j 即不超过背包剩余空间 j，此时这些选法中能装入背包的最大物品价值！

状态转移方程

​ 其实这个状态转移方程并不难，我们根据之前的经验，就是根据最后一步的状态来分情况，这里很明显，就是 i 处的物品选还是不选的情况：

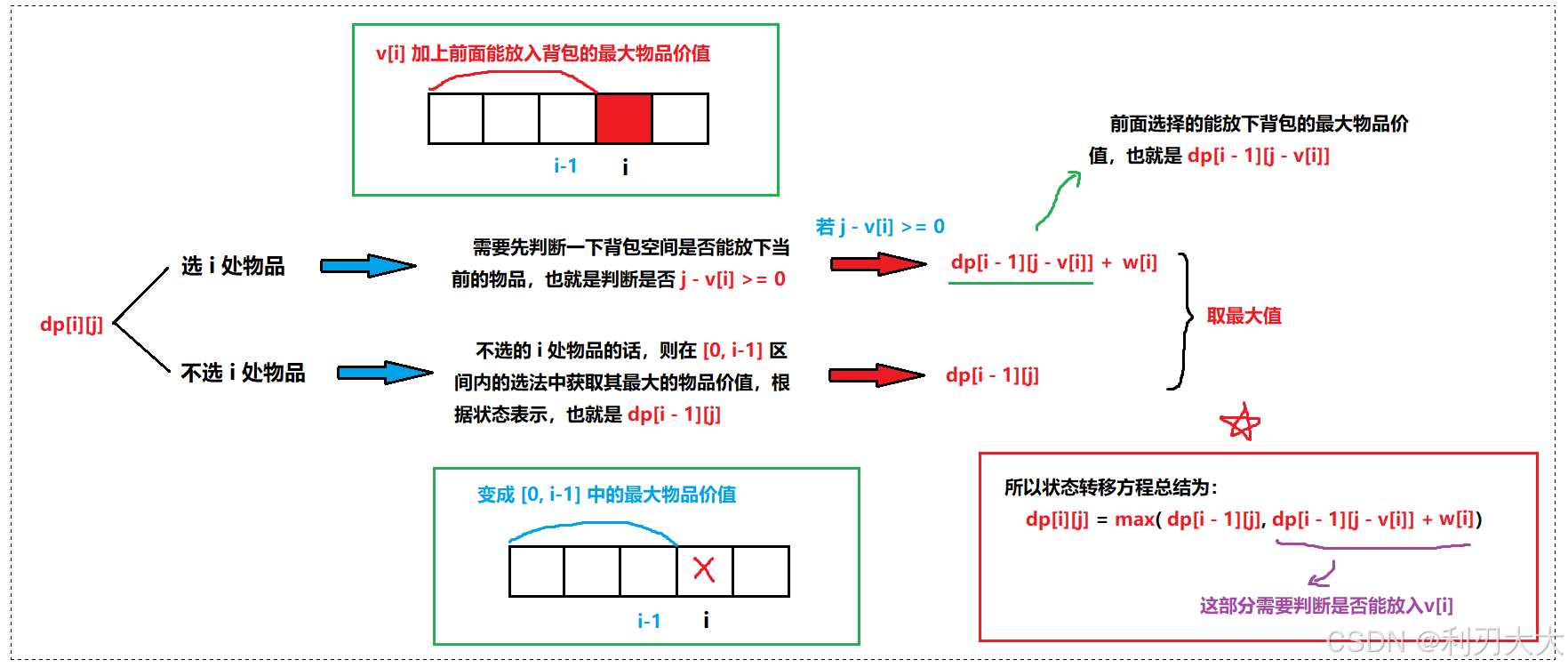
初始化

​ 因为我们会开辟虚拟行列，所以我们要初始化一下虚拟行列，保证对后面填表的正确性！其实只需要 都初始化为 0 即可，因为第一行也就是 dp[0][j] 就表示没有物品可以放，肯定就是 0；而 dp[i][0] 表示的是背包空间只有 0 了，放不下了，所以只能为 0 啦！

遍历顺序

​ 因为用到了上方和可能左上方的区域，所以 从上往下，从左往右遍历 即可！

返回值

​ 由状态表示可知我们就是要返回 dp[n][V]。

2、第二问解题思路

​ 我们顺便解决了第二问再一起给出题解，因为这道题在牛客网中找的，两道题连在了一起！

​ 第二问其实就是在第一问的基础之上修改一些细节，大体的思路还是一样的！修改的点主要体现在状态表示、状态转移方程细节和初始化，其它都是一样的，下面我们来细讲一下！

状态表示修改

​ 因为题目要求变了，所以我们得修改一下状态表示，其实就是改一下对于背包容量的要求即可！

​ 所以状态表示为：dp[i][j] 表示从前 i 个物品中选择，并且物品总体积正好等于背包空间 j，此时这些选法中能装入背包的最大物品价值！

状态转移方程细节修改

​ 大体的状态转移方程和第一问是一样的，只不过根据现在的状态表示，我们必须要判断一下 当我们选择 v[i] 也就是当前物品加入背包的时候，原状态转移方程需要用到 dp[i - 1][j - v[i]]，此时我们就需要知道 dp[i - 1][j - v[i]] 是否是能构成 j - v[i] 的背包空间大小，如果连 dp[i - 1][j - v[i]] 的体积都无法达到其背包空间的话，我们就 认为当前选中 v[i] 之后，总体积是无法等于 j 的，就不做处理！

​ 为了方便判断某个 dp 值是否能构成其对应的背包空间，我们 设定 dp[i][j] == -1 表示选择 i 物品之后，其总体积无法等于背包空间 j，而非 -1 的情况就代表其最大物品价值！

​ 所以修改完的状态转移方程如下所示：

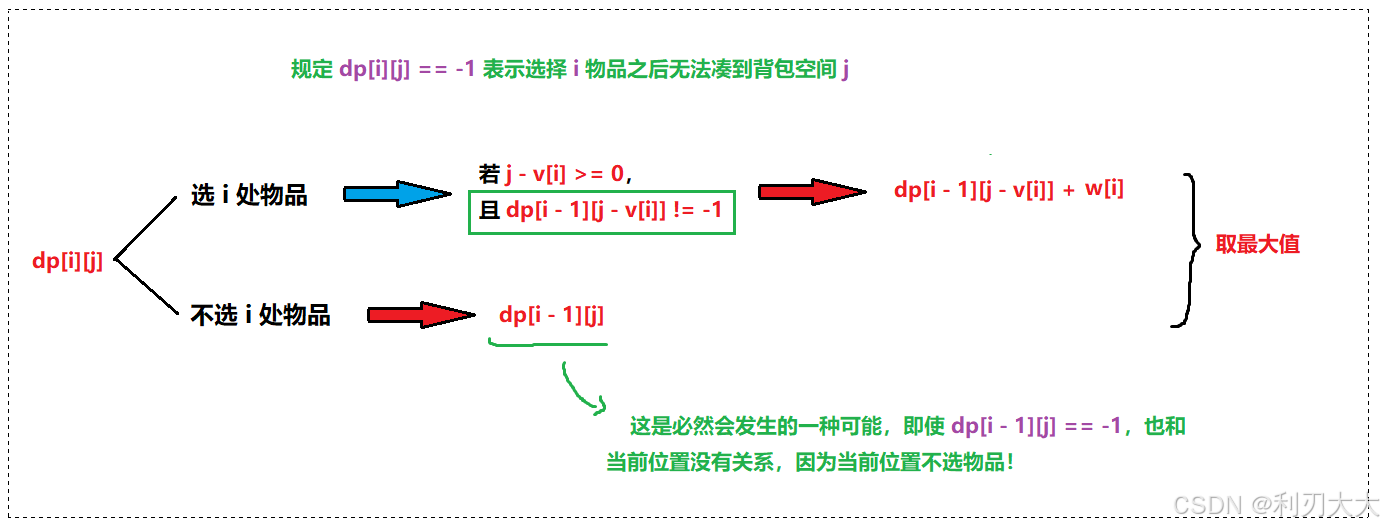
​ 上图还解析了为什么不选 i 处物品的情况是必定要考虑的！

​ 但是可能还会有人问，为什么不规定 dp[i][j] == 0 的时候表示选择 i 物品之后无法凑到背包空间 j 呢❓❓❓

​ 这是因为我们 dp[i][j] == 0 已经表示此时最大物品价值为 0，它不能够去充当两个状态使用，所以我们规定其为 -1。

初始化修改

​ 初始化就不像我们之前题目那样子直接初始化为 0 了，因为我们还多了个状态 -1，并且状态表示也变了，初始化的解析如下图所示：

代码

#include <iostream>
#include <cstring>
using namespace std;// 算法题定义为全局变量，默认初始化为0 -- 但是工程代码不建议这样子写！
const int N = 1010;
int n, V, v[N], w[N];
int dp[N][N];int main()
{int n, V;cin >> n >> V;// 填入题目给出的物品体积和价值的数组 -- 从下标为1开始for(int i = 1; i <= n; ++i)cin >> v[i] >> w[i];// 解决第一问：求这个背包至多能装多大价值的物品// 不需要初始化for(int i = 1;  i <= n; ++i){for(int j = 1; j <= V; ++j){dp[i][j] = dp[i - 1][j]; // 单独写在外面是防止j<v[i]时没更新到if(j >= v[i])dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);}}cout << dp[n][V] << endl;// 解决第二问：若背包恰好装满，求至多能装多大价值的物品memset(dp, 0, sizeof(dp)); // 先清空dp表// 第一行除了第一个元素之外其它元素初始化为-1for(int i = 1; i <= V; ++i)dp[0][i] = -1;for(int i = 1; i <= n; ++i){for(int j = 1; j <= V; ++j){dp[i][j] = dp[i - 1][j];if(j >= v[i] && dp[i - 1][j - v[i]] != -1)dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);}}cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl; // 最后打印的时候注意不能输出-1，因为这是我们自己规定的return 0;
}

💥优化

​ 背包问题基本上都是利用「滚动数组」来做空间上的优化，我们只需要在原来的代码上稍加修改就行了！

​ 那可能就有同学会问了，滚动数组是个啥❓❓❓

​ 下面我们来讲一个最原始的滚动数组模型：原来我们需要开辟一个 n*V 大小的二维数组，但是我们发现，每次遍历的时候我们只用到了 dp[i - 1][j] 和 dp[i - 1][j - v[i]]，那么此时 i-2、i-3 行岂不是浪费了吗，对不对，那我们就仔细一想，能不能只用两个一维数组来完成状态转移操作！

​ 没错，这就引出了最原始的滚动数组模型，如下所示：

​ 那么只靠这两个一维数组要如何达到一直能利用起来的效果呢，这就是滚动数组的功劳了！因为我们填完第 i 行之后，那么第 i-1 行其实就没用了，而第 i 行就要作为下一次的 i-1 行，而原来的第 i-1 行则变成了新的第 i 行！听着是不是有点绕，下面举个例子，假设我们从第 0 行开始：

​ 这就有了一种滚动的感觉，所以称之为滚动数组！但其实这是比较原始的滚动数组，我们其实 不需要两个一维数组，只需要一个一维数组就够了！

​ 这是怎么做到的呢，其实我们 只需要删除掉原来 dp[i][j] 中的 i 选项即可，如下图所示：

​ 对于这两问来说都是同样如此！

​ 但是这里有一个问题，就是如果我们是从左往右遍历这个数组的话，假设我们最外层的 for 循环中 i 的大小是 1，然后将数组进行了填表，此时 i 循环到了 2，那么就要重新去填表，填表的时候要用到 dp[j - v[i]]，但是此时假设 dp[2] 先被重新更新了，那它后面的 dp[3]、dp[4] 等状态值就无法获取到原来的 dp[2] 了，因为 dp[j - v[i]] 肯定是在前面的，那么此时该咋办呢❓❓❓

​ 很简单，我们 只需要修改一下遍历顺序，变成从右往左遍历，此时就是先遍历后面那些需要用到 j - v[i] 处元素的状态值，这样子一来就不会有前面被更新了的情况！

​ 总结一下，在 01 背包问题中，进行优化的操作其实就是：

• 删掉所有的横坐标
• 修改一下 j 的遍历顺序

​ 那么这些优化体现在哪里呢❓❓❓

• 首先是 空间优化，原来需要 n*V 大小的二维数组，现在我们只需要一个 V 大小的一维数组！
• 其次是 时间优化，这体现在 for 循环中，我们直接用 j >= v[i] 来作为判断条件，那么就不需要 j 每次都遍历到了 j >= 1才停下来！

优化后的代码

#include <iostream>
#include <cstring>
using namespace std;// 算法题定义为全局变量，默认初始化为0 -- 但是工程代码不建议这样子写！
const int N = 1010;
int n, V, v[N], w[N];
int dp[N]; // 只需要一维dp数组int main()
{int n, V;cin >> n >> V;// 填入题目给出的物品体积和价值的数组 -- 从下标为1开始for(int i = 1; i <= n; ++i)cin >> v[i] >> w[i];////////////////////////////////////  将i下标的选项都删除，改变j的遍历顺序  ///////////////////////////////// 解决第一问：求这个背包至多能装多大价值的物品// 不需要初始化for(int i = 1;  i <= n; ++i){for(int j = V; j >= v[i]; --j) // 改变遍历顺序，只需要遍历到v[i]即可{dp[j] = max(dp[j], dp[j - v[i]] + w[i]);}}cout << dp[V] << endl;// 解决第二问：若背包恰好装满，求至多能装多大价值的物品memset(dp, 0, sizeof(dp)); // 先清空dp表// 第一行除了第一个元素之外其它元素初始化为-1for(int j = 1; j <= V; ++j)dp[j] = -1;for(int i = 1; i <= n; ++i){for(int j = V; j >= v[i]; --j) // 改变遍历顺序，只需要遍历到v[i]即可{if(dp[j - v[i]] != -1)dp[j] = max(dp[j], dp[j - v[i]] + w[i]);}}cout << (dp[V] == -1 ? 0 : dp[V]) << endl; // 最后打印的时候注意不能输出-1，因为这是我们自己规定的return 0;
}