当前位置：首页 > news >正文

【一文了解】八大排序-计数排序

news 2025/11/4 15:00:04

1.计数排序

1.1.核心逻辑

1.2.适用场景

1.3.复杂度

1.4.稳定性

1.5.举例（升序为例）

1）核心动作拆解

2）实例分析（[2,0,2,1,1,0]）

1.6.代码实现

2.基数排序

2.1.核心逻辑

2.2.适用场景

2.3.复杂度

2.4.稳定性

2.5.举例（升序为例）

1）核心动作拆解

2）实例分析（[170,45,75,90,802,24,2,66]）

2.6.代码实现

3.桶排序

3.1.核心逻辑

3.2.适用场景

3.3.复杂度

3.4.稳定性

3.5.举例（升序为例）

1）核心动作拆解

2）实例分析（[0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434]）

3.6.代码实现

4.测试

4.1.完整代码

4.2.测试结果

5.总结

本篇文章来分享一下八大排序中的计数排序。同时也一起理解基数排序和桶排序。计数排序、基数排序、桶排序均属于属于非比较型排序算法（不通过元素间的比较实现排序），核心思想是利用“数据的分布特性”直接确定元素的位置，因此在特定场景下可突破比较排序的O(nlogn)时间下限，达到线性时间复杂度。

1.计数排序

1.1.核心逻辑

①统计每个元素出现次数；②计算元素在有序数组中的位置；③按位置填充元素，生成有序数组

1.2.适用场景

数据范围小且为整数的场景（如成绩排序：0~100、年龄排序：0~150、ID排序：固定范围）

1.3.复杂度

1）时间复杂度：O(n+k)（n=数组长度，k=数据范围，统计和填充均为线性时间）

2）空间复杂度：O(n+k)（n=数组长度，k=数据范围，需计数数组和输出数组）

1.4.稳定性

稳定（倒序遍历填充元素，相同元素按原数组顺序保留）

1.5.举例（升序为例）

1）核心动作拆解

●统计次数：创建“计数数组”，用索引对应“待排序元素的值”，用数组元素对应“该值的出现次数”（若元素值有负数，需通过“偏移量”将值映射为非负索引）。

●计算位置：将计数数组转换为“前缀和数组”，前缀和表示“小于等于当前值的元素总数”，由此确定每个元素在有序数组中的最后一个位置（保证稳定性）。

●填充结果：倒序遍历原数组，根据前缀和数组找到每个元素的最终位置，填充到输出数组，同时更新前缀和（确保下一个相同元素的位置正确）。

2）实例分析（[2,0,2,1,1,0]）

步骤 1：确定基础参数

    待排序数组 arr = [2, 0, 2, 1, 1, 0]（长度 n=6）。

    元素最小值 minValue=0，最大值 maxValue=2 → 数据范围 range = 2-0+1=3（计数数组长度为 3）。

步骤 2：统计每个元素的出现次数（计数数组）

    创建计数数组 countArr（索引 0→值 0，索引 1→值 1，索引 2→值 2），遍历原数组统计次数：

    元素 0 出现 2 次 → countArr[0] = 2。

    元素 1 出现 2 次 → countArr[1] = 2。

    元素 2 出现 2 次 → countArr[2] = 2。

    此时 countArr = [2, 2, 2]。

步骤 3：计算前缀和（确定元素最终位置）

    升序排序时，前缀和从左到右计算，含义是“小于等于当前值的元素总数”：

    countArr[0] 不变 → 2（≤0 的元素有 2 个）。

    countArr[1] = countArr[1] + countArr[0] = 2+2=4（≤1 的元素有 4 个）。

    countArr[2] = countArr[2] + countArr[1] = 2+4=6（≤2 的元素有 6 个）。

    此时前缀和数组 countArr = [2, 4, 6]，每个索引的前缀和即“该值在有序数组中的最后一个位置 + 1”（因数组索引从 0 开始）。

步骤 4：倒序遍历原数组，填充输出数组（保证稳定性）

    创建输出数组 outputArr（长度 6），从原数组末尾（索引 5）开始遍历，逐个确定元素位置：

    ●原数组索引 5：元素 0

        计数索引 = 0 - 0 = 0 → 前缀和 countArr[0] = 2。

        最终位置 = 2 - 1 = 1 → outputArr[1] = 0。

        更新前缀和：countArr[0] = 2-1=1（下一个 0 的位置为 0）。

    ●原数组索引 4：元素 1

        计数索引 = 1 - 0 = 1 → 前缀和 countArr[1] = 4。

        最终位置 = 4 - 1 = 3 → outputArr[3] = 1。

        更新前缀和：countArr[1] = 4-1=3（下一个 1 的位置为 2）。

    ●原数组索引 3：元素 1

        计数索引 = 1 - 0 = → 前缀和 countArr[1] = 3。

        最终位置 = 3 - 1 = 2 → outputArr[2] = 1。

        更新前缀和：countArr[1] = 3-1=2。

    ●原数组索引 2：元素 2

        计数索引 = 2 - 0 = → 前缀和 countArr[2] = 6。

        最终位置 = 6 - 1 = 5 → outputArr[5] = 2。

        更新前缀和：countArr[2] = 6-1=5（下一个 2 的位置为 4）。

    ●原数组索引 1：元素 0

        计数索引 = 0 - 0 = → 前缀和 countArr[0] = 1。

        最终位置 = 1 - 1 = 0 → outputArr[0] = 0。

        更新前缀和：countArr[0] = 1-1=0。

    ●原数组索引 0：元素 2

        计数索引 = 2 - 0 = → 前缀和 countArr[2] = 5。

        最终位置 = 5 - 1 = 4 → outputArr[4] = 2。

        更新前缀和：countArr[2] = 5-1=4。

步骤 5：输出最终结果

    输出数组 outputArr = [0, 0, 1, 1, 2, 2]，将其复制回原数组，排序完成。

1.6.代码实现

/// <summary>
/// 计数排序（非比较排序，基于"统计元素出现次数"实现）
/// </summary>
/// <param name="arr">待排序数组（会直接修改原数组）</param>
/// <param name="minValue">数组中元素的最小值（需提前确定，非比较排序依赖数据范围）</param>
/// <param name="maxValue">数组中元素的最大值（需提前确定）</param>
/// <param name="isAscending">排序方向：true=升序，false=降序</param>
public static void CountingSort<T>(T[] arr, T minValue, T maxValue, bool isAscending = true) where T : IComparable<T>
{//校验输入：空数组或长度为1，无需排序if (arr == null || arr.Length <= 1) return;//校验类型：确保T是数值类型（因需转换为int计算范围）if (!typeof(T).IsValueType || typeof(T) == typeof(bool)){throw new ArgumentException("计数排序仅支持数值类型（如int、long），不支持引用类型或bool");}//1.将泛型数值转换为int，计算数据范围（k = max - min + 1）int min = Convert.ToInt32(minValue);int max = Convert.ToInt32(maxValue);int range = max - min + 1;//2.创建计数数组，统计每个元素出现次数（索引=元素-min，避免负索引）int[] countArr = new int[range];foreach (T item in arr){int itemInt = Convert.ToInt32(item);int countIndex = itemInt - min;countArr[countIndex]++;}//3.计算"前缀和"，确定每个元素在有序数组中的结束位置（用于稳定排序）//前缀和的本质是“元素的累计出现次数”，其值 = 元素最后一个位置 + 1。if (isAscending){//升序：前缀和从左到右计算（元素位置递增）for (int i = 1; i < range; i++){countArr[i] += countArr[i - 1];}}else{//降序：前缀和从右到左计算（元素位置递减）for (int i = range - 2; i >= 0; i--){countArr[i] += countArr[i + 1];}}//4.创建输出数组，倒序遍历原数组填充（保证稳定性：相同元素按原顺序保留）T[] outputArr = new T[arr.Length];for (int i = arr.Length - 1; i >= 0; i--){int itemInt = Convert.ToInt32(arr[i]);int countIndex = itemInt - min;//计算当前元素在输出数组中的位置（countArr[countIndex]-1：因countArr存储的是"元素个数"，索引从0开始）int outputIndex = countArr[countIndex] - 1;outputArr[outputIndex] = arr[i];//减少计数（下一个相同元素的位置向前/向后移1）countArr[countIndex]--;}//5.将有序的输出数组复制回原数组Array.Copy(outputArr, 0, arr, 0, outputArr.Length);
}
/// <summary>
/// 自动获取数组的最小值和最大值（简化调用）
/// </summary>
public static void CountingSortAutoRange<T>(T[] arr, bool isAscending = true) where T : IComparable<T>
{if (arr == null || arr.Length <= 1) return;//遍历数组，找到最小值和最大值T min = arr[0];T max = arr[0];foreach (T item in arr){if (item.CompareTo(min) < 0) min = item;if (item.CompareTo(max) > 0) max = item;}//调用核心计数排序方法CountingSort(arr, min, max, isAscending);
}

2.基数排序

2.1.核心逻辑

①确定排序层级：找到数组中最大数，确定最大位数；②按位排序：按"个位→十位→百位..."依次排序；③传递有序性：逐步放大排序粒度，最终有序

2.2.适用场景

多位数/大范围整数（如身份证号、手机号、1~100000的整数），避免计数排序"范围过大导致空间浪费"问题

2.3.复杂度

1）时间复杂度：O(d*(n+k))（d=最大位数，n=数组长度，k=单一位数范围(0~9)，实际近似O(n)）

2）空间复杂度：O(n+k)（计数排序所需空间）

2.4.稳定性

稳定（依赖计数排序的稳定性，相同位数的元素保留原顺序）

2.5.举例（升序为例）

1）核心动作拆解

●确定排序层级：找到数组中最大数的“位数”（如最大数是123，则有3位），决定需要排序的总层级（个位→十位→百位）。

●按位排序：从最低位（个位）到最高位，对每一位单独执行“计数排序”（因单一位数范围固定为0~9，计数排序效率极高）。

●传递有序性：每完成一位排序，数组在该位上已有序；当最高位排序完成后，整个数组因“高位优先”的特性自然整体有序。

2）实例分析（[170,45,75,90,802,24,2,66]）

步骤 1：确定最大数和总位数

    数组中最大数是 802，其位数为 3 位（个位、十位、百位），因此需要排序 3 轮（个位→十位→百位）。

步骤 2：第 1 轮排序（按个位）让数组按“个位数字”升序排列。

    ●提取个位数字：170→0，45→5，75→5，90→0，802→2，24→4，2→2，66→6。

    ●计数排序（按个位）：

        计数数组 countArr[10] ，表示0~9，统计个位数字出现次数：countArr = [2,0,2,0,1,2,1,0,0,0]（0 出现 2 次，2 出现 2 次，4 出现 1 次，5 出现 2 次，6 出现 1 次）。

        计算前缀和：countArr = [2,2,4,4,5,7,8,8,8,8]（用于确定每个个位数字的最终位置）。

        倒序填充输出数组（保证稳定性）：输出数组按个位升序为 [170, 90, 802, 2, 24, 45, 75, 66]。

步骤 3：第 2 轮排序（按十位）在“个位有序”的基础上，让数组按“十位数字”升序排列。

    ●提取十位数字：170→7，90→9，802→0，2→0，24→2，45→4，75→7，66→6。

    ●计数排序（按十位）：

        计数数组统计十位数字出现次数：countArr = [2,0,1,0,1,0,1,2,0,1]（0 出现 2 次，2 出现 1 次，4 出现 1 次，6 出现 1 次，7 出现 2 次，9 出现 1 次）。

        计算前缀和：countArr = [2,2,3,3,4,4,5,7,7,8]。

        倒序填充输出数组（基于上一轮结果，保证稳定性）：输出数组按十位升序为 [802, 2, 24, 45, 66, 170, 75, 90]。

步骤 4：第 3 轮排序（按百位）在“十位有序”的基础上，让数组按“百位数字”升序排列。

    ●提取百位数字：802→8，2→0，24→0，45→0，66→0，170→1，75→0，90→0。

    ●计数排序（按百位）：

        计数数组统计百位数字出现次数：countArr = [5,1,0,0,0,0,0,0,1,0]（0 出现 5 次，1 出现 1 次，8 出现 1 次）。

        计算前缀和：countArr = [5,6,6,6,6,6,6,6,7,7]。

        倒序填充输出数组：输出数组按百位升序为 [2, 24, 45, 66, 75, 90, 170, 802]。

最终结果

经过 3 轮按位排序后，数组完全有序：[2, 24, 45, 66, 75, 90, 170, 802]。

2.6.代码实现

    /// <summary>/// 基数排序（非比较排序，基于"按位排序+计数排序"实现）/// </summary>/// <param name="arr">待排序数组（非负整数，直接修改原数组）</param>/// <param name="isAscending">排序方向：true=升序，false=降序</param>public static void RadixSort(int[] arr, bool isAscending = true){//1.校验输入：空数组或长度为1，无需排序if (arr == null || arr.Length <= 1) return;//2.找到数组中最大数，确定"最大位数"（如123的最大位数是3）int maxNum = arr[0];foreach (int num in arr){if (num < 0)throw new ArgumentException("基数排序默认支持非负整数，负数需先处理（如加偏移量）");if (num > maxNum)maxNum = num;}//3.按"位"排序：从个位（d=1）到最大位（d=10^(maxDigit-1)）for (int d = 1; maxNum / d > 0; d *= 10){//对当前位（d位）执行计数排序（核心：提取当前位的数值作为排序依据）CountSortByDigit(arr, d, isAscending);}}/// <summary>/// 按"指定位"（d）排序（基于计数排序实现）/// </summary>/// <param name="arr">待排序数组</param>/// <param name="d">当前排序的"位"（如d=1→个位，d=10→十位，d=100→百位）</param>/// <param name="isAscending">排序方向</param>private static void CountSortByDigit(int[] arr, int d, bool isAscending){int n = arr.Length;int[] outputArr = new int[n];//输出数组（存储当前位排序后的结果）int[] countArr = new int[10];//计数数组（单一位数范围0~9，固定长度10）//1.统计当前位（d位）的数值出现次数foreach (int num in arr){//提取当前位的数值：(num / d) % 10（如num=123，d=10→(123/10)=12→12%10=2→十位是2）int digit = (num / d) % 10;countArr[digit]++;}//2.计算前缀和，确定当前位数值在输出数组中的位置（保证稳定性）if (isAscending){//升序：前缀和从左到右（0→9）for (int i = 1; i < 10; i++){countArr[i] += countArr[i - 1];}}else{//降序：前缀和从右到左（9→0）for (int i = 8; i >= 0; i--){countArr[i] += countArr[i + 1];}}//3.倒序遍历原数组，按当前位数值填充输出数组（保证稳定性）for (int i = n - 1; i >= 0; i--){int digit = (arr[i] / d) % 10;int outputIndex = countArr[digit] - 1;//计数数组存"元素个数"，索引从0开始需减1outputArr[outputIndex] = arr[i];countArr[digit]--;//下一个相同位数值的位置前移}//4.将当前位排序后的结果复制回原数组，为下一位排序做准备Array.Copy(outputArr, 0, arr, 0, n);}/// <summary>/// 支持负数的基数排序（通过"加偏移量"将负数转为非负）/// </summary>public static void RadixSortWithNegative(int[] arr, bool isAscending = true){if (arr == null || arr.Length <= 1) return;//找到最小负数，计算偏移量（让所有数转为非负：num + offset ≥ 0）int minNum = arr[0];foreach (int num in arr){if (num < minNum)minNum = num;}int offset = minNum < 0 ? -minNum : 0;//若有负数，偏移量为"最小负数的绝对值"//1.所有数加偏移量，转为非负for (int i = 0; i < arr.Length; i++){arr[i] += offset;}//2.执行普通基数排序RadixSort(arr, isAscending);//3.减去偏移量，恢复原数值for (int i = 0; i < arr.Length; i++){arr[i] -= offset;}}

3.桶排序

3.1.核心逻辑

①分桶，确定数据范围，创建桶；根据数据值计算“桶索引”，将每个元素放入对应的桶中；②桶内排序：对每个非空桶单独排序；③合并桶

3.2.适用场景

数据分布均匀的浮点数或整数

3.3.复杂度

1）时间复杂度：O(n)（平均/理想情况：数据均匀分布，桶数量合理），O(n²)（最坏情况：数据集中在一个桶，且桶内用低效排序）

时间复杂度=分桶时间+所有桶内排序的总时间+合并桶时间=O(n)+O(Σ(n_ilogn_i))+O(n)

●分桶时间：O(n)

遍历所有数据，计算每个元素的桶索引并放入对应桶中，每个元素的处理时间为O(1)（索引计算是常数级操作），因此分桶时间为O(n)。

●所有桶内排序的总时间：O(Σ(n_ilogn_i))

每个桶内的数据需要单独排序（通常用快速排序、插入排序等）。假设每个桶用O(mlogm)时间的排序算法（m为桶内数据量），则第i个桶的排序时间为O(n_ilogn_i)，所有桶的总时间为各桶之和：O(n_1logn_1+n_2logn_2+...+n_klogn_k)。

1）理想情况（数据均匀分布）：O(n)

若数据在桶中均匀分布，每个桶的数量n_i≈n/k（约等于n除以k）。此时：Σ(n_ilogn_i)≈k×(n/k)×log(n/k)=n×log(n/k)

若k为常数（如k=10）：log(n/k)≈logn，总时间为O(nlogn)；

若k与n成正比（如k=n，每个桶1个元素）：log(n/k)=log1=0，此时Σ(n_ilogn_i)=0，总时间为O(n)；

工程中常取k≈√n（平衡时间和空间），此时log(n/k)≈log√n=(1/2)logn，总时间近似O(nlogn)，但系数远小于直接排序（因每个桶的排序规模小）。

2）极端情况（数据集中在一个桶）：O(n²)

若数据分布极不均匀（如所有元素都落入同一个桶），则k=1，n_1=n，其他桶为空。此时：Σ(n_ilogn_i)=nlogn（若用快速排序）或n²（若用冒泡排序）。

●合并桶时间：O(n)

按桶索引顺序遍历所有桶，将元素依次取出拼接成结果数组，本质是遍历所有n个元素，合并桶时间为O(n)。

2）空间复杂度：O(n+k)

3.4.稳定性

桶内用稳定排序时稳定，最常用插入排序（小规模）和归并排序（中规模）

3.5.举例（升序为例）

1）核心动作拆解

●分桶（分配数据）：确定数据范围（最大值max和最小值min），创建k个空桶（k为自定义桶数量）；根据数据值计算“桶索引”，将每个元素放入对应的桶中（确保桶之间的元素范围不重叠，且按桶索引递增/递减）。

●桶内排序：对每个非空桶单独排序（可复用插入排序、快速排序等，因单桶数据量小，排序效率高）。

●合并桶：按桶索引顺序依次取出所有桶中的元素，拼接成最终的有序数组。

根据数据值计算“桶索引”需要用到“线性比例映射”方法。

“线性比例映射”方法是通用的数值映射思路，常用于“一个数值范围映射到另一个固定范围”的场景。核心是“保持数值的相对位置不变”，通过线性计算实现范围转换。

映射本质是“线性缩放”，其通用公式可抽象为：假设需要将原范围[A_min,A_max]的数值x，映射到目标范围[B_min,B_max]的数值y，则映射公式为：

y=B_min+(x-A_min)×(B_max-B_min)/(A_max-A_min)

当x=A_min时，y=B_min（原范围最小值对应目标范围最小值）；

当x=A_max时，y=B_max（原范围最大值对应目标范围最大值）；

中间值按比例缩放，保持相对位置不变。

桶排序的索引映射是这个通用公式的简化版（目标范围固定为[0,k-1]，即B_min=0，B_max=k-1），代入后就是之前的桶索引公式：桶索引=0+(x-min)×(k-1-0)/(max-min)=(x-min)×(k-1)/(max-min)

2）实例分析（[0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434]）

假设桶数量 k=4。

步骤 1：确定数据范围并创建桶

    计算 min=0.1234，max=0.897；

    创建 4 个空桶：bucket[0]、bucket[1]、bucket[2]、bucket[3]。

步骤 2：分桶（计算每个元素的桶索引）

    桶索引计算公式（将 [min, max] 均匀映射到 [0, k-1]）：桶索引 = (元素值 - min) × (k-1) ÷ (max - min)

        0.897：(0.897-0.1234)×3÷(0.897-0.1234) = 3 → 放入 bucket[3]

        0.565：(0.565-0.1234)×3÷0.7736 ≈ 1.7 → 取整数 1 → 放入 bucket[1]

        0.656：(0.656-0.1234)×3÷0.7736 ≈ 2.1 → 取整数 2 → 放入 bucket[2]

        0.1234：(0.1234-0.1234)×3÷0.7736 = 0 → 放入 bucket[0]

        0.665：(0.665-0.1234)×3÷0.7736 ≈ 2.1 → 取整数 2 → 放入 bucket[2]

        0.3434：(0.3434-0.1234)×3÷0.7736 ≈ 0.85 → 取整数 0 → 放入 bucket[0]

    分桶后结果：

        bucket[0] = [0.1234, 0.3434]

        bucket[1] = [0.565]

        bucket[2] = [0.656, 0.665]

        bucket[3] = [0.897]

步骤 3：桶内排序

    对每个桶单独升序排序（此处用简单插入排序）：

    bucket[0] 排序后：[0.1234, 0.3434]（已有序）

    bucket[1] 排序后：[0.565]（单元素无需排序）

    bucket[2] 排序后：[0.656, 0.665]（已有序）

    bucket[3] 排序后：[0.897]（单元素无需排序）

步骤 4：合并桶

    按桶索引顺序（0→1→2→3）拼接所有桶的元素：

3.6.代码实现

/// <summary>
/// 插入排序
/// </summary>
/// <param name="arr">待排序数组（会直接修改原数组）</param>
/// <param name="isAscending">排序方向：true=升序，false=降序</param>
public static void InsertionSort<T>(T[] arr, bool isAscending = true) where T : IComparable<T>
{if (arr == null || arr.Length <= 1) return;int n = arr.Length;//外层循环：从第2个元素开始（第1个元素默认已序）for (int i = 1; i < n; i++){T current = arr[i];//待插入的"当前元素"（暂存，避免后续移位覆盖）int j = i - 1;     //已排序部分的末尾索引//内层循环：将"已排序部分"中比current大/小的元素后移，腾出插入位置while (j >= 0){int compareResult = arr[j].CompareTo(current);bool needSwap = isAscending ? (compareResult > 0) : (compareResult < 0);if (needSwap){arr[j + 1] = arr[j];//元素后移j--;}else{break;//找到插入位置，退出循环}}//将current插入到正确位置（j+1：因循环结束时j已多减1）arr[j + 1] = current;}
}
/// <summary>
/// 桶排序
/// </summary>
/// <param name="arr">待排序数组（支持int、long、float、double）</param>
/// <param name="bucketCount">桶数量（默认10，可根据数据分布调整）</param>
/// <param name="isAscending">排序方向：true=升序，false=降序</param>
public static void BucketSort<T>(T[] arr, int bucketCount = 10, bool isAscending = true) where T : IComparable<T>
{//输入校验if (arr == null || arr.Length <= 1 || bucketCount <= 0) return;//1.确定数据范围（最大值和最小值）T min = arr[0];T max = arr[0];foreach (var item in arr){if (item.CompareTo(min) < 0) min = item;if (item.CompareTo(max) > 0) max = item;}//2.创建桶（用链表或列表存储，此处用List<T>）List<T>[] buckets = new List<T>[bucketCount];for (int i = 0; i < bucketCount; i++){buckets[i] = new List<T>();}//3.将元素分配到对应桶中（根据值的范围计算桶索引）foreach (var item in arr){//计算桶索引：将[min, max]映射到[0, bucketCount-1]int bucketIndex = CalculateBucketIndex(item, min, max, bucketCount);buckets[bucketIndex].Add(item);}//4.对每个桶单独排序（此处复用系统排序，也可替换为其他排序如插入排序）foreach (var bucket in buckets){//bucket.Sort();//系统排序默认升序，为非稳定排序//if (!isAscending)//{//    bucket.Reverse();//降序时反转桶内元素//}//最常用插入排序T[] arrTest = bucket.ToArray();if (isAscending)InsertionSort(arrTest);elseInsertionSort(arrTest, false);bucket.Clear();bucket.AddRange(arrTest);}//5.合并所有桶的元素到原数组int arrIndex = 0;foreach (var bucket in buckets){foreach (var item in bucket){arr[arrIndex++] = item;}}
}
/// <summary>
/// 计算元素应放入的桶索引
/// </summary>
private static int CalculateBucketIndex<T>(T item, T min, T max, int bucketCount) where T : IComparable<T>
{//处理数值类型（int/long/float/double）if (typeof(T) == typeof(int)){int itemInt = Convert.ToInt32(item);int minInt = Convert.ToInt32(min);int maxInt = Convert.ToInt32(max);if (maxInt == minInt) return 0;//所有元素相等时放入第0桶return (int)((itemInt - minInt) * (bucketCount - 1) / (double)(maxInt - minInt));}else if (typeof(T) == typeof(long)){long itemLong = Convert.ToInt64(item);long minLong = Convert.ToInt64(min);long maxLong = Convert.ToInt64(max);if (maxLong == minLong) return 0;return (int)((itemLong - minLong) * (bucketCount - 1) / (double)(maxLong - minLong));}else if (typeof(T) == typeof(float) || typeof(T) == typeof(double)){double itemDouble = Convert.ToDouble(item);double minDouble = Convert.ToDouble(min);double maxDouble = Convert.ToDouble(max);if (maxDouble == minDouble) return 0;return (int)((itemDouble - minDouble) * (bucketCount - 1) / (maxDouble - minDouble));}else{throw new ArgumentException("桶排序仅支持数值类型（int/long/float/double）");}
}

4.测试

4.1.完整代码

using System;
using System.Collections.Generic;
using UnityEngine;public class SortTest : MonoBehaviour
{private void Start(){int[] arr8 = GenerateArray(10);PrintArray(arr8);CountingSortAutoRange(arr8);PrintArray(arr8, "计数排序后，数组内容：");arr8 = GenerateArray(10,0,12);PrintArray(arr8);CountingSort(arr8, 0, 12);PrintArray(arr8, "计数排序后，数组内容：");int[] arr9 = GenerateArray(10);PrintArray(arr9);RadixSort(arr9);PrintArray(arr9, "基数排序后，数组内容：");arr9 = GenerateArray(10, -100, 100);PrintArray(arr9);RadixSortWithNegative(arr9);PrintArray(arr9, "基数排序后，数组内容：");int[] arr10 = GenerateArray(16);PrintArray(arr10);BucketSort(arr10, 4);PrintArray(arr10, "桶排序后，数组内容：");double[] arr11 = new double[] { 0.1, 0.9, 0.41, 0.21 };PrintArray(arr11);BucketSort(arr11, 2);PrintArray(arr11, "桶排序后，数组内容：");}/// <summary>/// 生成数组/// </summary>/// <param name="count"></param>/// <param name="minValue"></param>/// <param name="maxValue"></param>/// <returns></returns>private int[] GenerateArray(int count, int minValue = 0, int maxValue = 100){List<int> arr = new List<int>();for (int i = 0; i < count; i++){int value = UnityEngine.Random.Range(minValue, maxValue);arr.Add(value);}return arr.ToArray();}/// <summary>/// 插入排序/// </summary>/// <param name="arr">待排序数组（会直接修改原数组）</param>/// <param name="isAscending">排序方向：true=升序，false=降序</param>public static void InsertionSort<T>(T[] arr, bool isAscending = true) where T : IComparable<T>{if (arr == null || arr.Length <= 1) return;int n = arr.Length;//外层循环：从第2个元素开始（第1个元素默认已序）for (int i = 1; i < n; i++){T current = arr[i];//待插入的"当前元素"（暂存，避免后续移位覆盖）int j = i - 1;     //已排序部分的末尾索引//内层循环：将"已排序部分"中比current大/小的元素后移，腾出插入位置while (j >= 0){int compareResult = arr[j].CompareTo(current);bool needSwap = isAscending ? (compareResult > 0) : (compareResult < 0);if (needSwap){arr[j + 1] = arr[j];//元素后移j--;}else{break;//找到插入位置，退出循环}}//将current插入到正确位置（j+1：因循环结束时j已多减1）arr[j + 1] = current;}}/// <summary>/// 计数排序（非比较排序，基于"统计元素出现次数"实现）/// </summary>/// <param name="arr">待排序数组（会直接修改原数组）</param>/// <param name="minValue">数组中元素的最小值（需提前确定，非比较排序依赖数据范围）</param>/// <param name="maxValue">数组中元素的最大值（需提前确定）</param>/// <param name="isAscending">排序方向：true=升序，false=降序</param>public static void CountingSort<T>(T[] arr, T minValue, T maxValue, bool isAscending = true) where T : IComparable<T>{//校验输入：空数组或长度为1，无需排序if (arr == null || arr.Length <= 1) return;//校验类型：确保T是数值类型（因需转换为int计算范围）if (!typeof(T).IsValueType || typeof(T) == typeof(bool)){throw new ArgumentException("计数排序仅支持数值类型（如int、long），不支持引用类型或bool");}//1.将泛型数值转换为int，计算数据范围（k = max - min + 1）int min = Convert.ToInt32(minValue);int max = Convert.ToInt32(maxValue);int range = max - min + 1;//2.创建计数数组，统计每个元素出现次数（索引=元素-min，避免负索引）int[] countArr = new int[range];foreach (T item in arr){int itemInt = Convert.ToInt32(item);int countIndex = itemInt - min;countArr[countIndex]++;}//3.计算"前缀和"，确定每个元素在有序数组中的结束位置（用于稳定排序）//前缀和的本质是“元素的累计出现次数”，其值 = 元素最后一个位置 + 1。if (isAscending){//升序：前缀和从左到右计算（元素位置递增）for (int i = 1; i < range; i++){countArr[i] += countArr[i - 1];}}else{//降序：前缀和从右到左计算（元素位置递减）for (int i = range - 2; i >= 0; i--){countArr[i] += countArr[i + 1];}}//4.创建输出数组，倒序遍历原数组填充（保证稳定性：相同元素按原顺序保留）T[] outputArr = new T[arr.Length];for (int i = arr.Length - 1; i >= 0; i--){int itemInt = Convert.ToInt32(arr[i]);int countIndex = itemInt - min;//计算当前元素在输出数组中的位置（countArr[countIndex]-1：因countArr存储的是"元素个数"，索引从0开始）int outputIndex = countArr[countIndex] - 1;outputArr[outputIndex] = arr[i];//减少计数（下一个相同元素的位置向前/向后移1）countArr[countIndex]--;}//5.将有序的输出数组复制回原数组Array.Copy(outputArr, 0, arr, 0, outputArr.Length);}/// <summary>/// 自动获取数组的最小值和最大值/// </summary>public static void CountingSortAutoRange<T>(T[] arr, bool isAscending = true) where T : IComparable<T>{if (arr == null || arr.Length <= 1) return;//遍历数组，找到最小值和最大值T min = arr[0];T max = arr[0];foreach (T item in arr){if (item.CompareTo(min) < 0) min = item;if (item.CompareTo(max) > 0) max = item;}//调用核心计数排序方法CountingSort(arr, min, max, isAscending);}/// <summary>/// 基数排序（非比较排序，基于"按位排序+计数排序"实现）/// </summary>/// <param name="arr">待排序数组（非负整数，直接修改原数组）</param>/// <param name="isAscending">排序方向：true=升序，false=降序</param>public static void RadixSort(int[] arr, bool isAscending = true){//1.校验输入：空数组或长度为1，无需排序if (arr == null || arr.Length <= 1) return;//2.找到数组中最大数，确定"最大位数"（如123的最大位数是3）int maxNum = arr[0];foreach (int num in arr){if (num < 0)throw new ArgumentException("基数排序默认支持非负整数，负数需先处理（如加偏移量）");if (num > maxNum)maxNum = num;}//3.按"位"排序：从个位（d=1）到最大位（d=10^(maxDigit-1)）for (int d = 1; maxNum / d > 0; d *= 10){//对当前位（d位）执行计数排序（核心：提取当前位的数值作为排序依据）CountSortByDigit(arr, d, isAscending);}}/// <summary>/// 按"指定位"（d）排序（基于计数排序实现）/// </summary>/// <param name="arr">待排序数组</param>/// <param name="d">当前排序的"位"（如d=1→个位，d=10→十位，d=100→百位）</param>/// <param name="isAscending">排序方向</param>private static void CountSortByDigit(int[] arr, int d, bool isAscending){int n = arr.Length;int[] outputArr = new int[n];//输出数组（存储当前位排序后的结果）int[] countArr = new int[10];//计数数组（单一位数范围0~9，固定长度10）//1.统计当前位（d位）的数值出现次数foreach (int num in arr){//提取当前位的数值：(num / d) % 10（如num=123，d=10→(123/10)=12→12%10=2→十位是2）int digit = (num / d) % 10;countArr[digit]++;}//2.计算前缀和，确定当前位数值在输出数组中的位置（保证稳定性）if (isAscending){//升序：前缀和从左到右（0→9）for (int i = 1; i < 10; i++){countArr[i] += countArr[i - 1];}}else{//降序：前缀和从右到左（9→0）for (int i = 8; i >= 0; i--){countArr[i] += countArr[i + 1];}}//3.倒序遍历原数组，按当前位数值填充输出数组（保证稳定性）for (int i = n - 1; i >= 0; i--){int digit = (arr[i] / d) % 10;int outputIndex = countArr[digit] - 1;//计数数组存"元素个数"，索引从0开始需减1outputArr[outputIndex] = arr[i];countArr[digit]--;//下一个相同位数值的位置前移}//4.将当前位排序后的结果复制回原数组，为下一位排序做准备Array.Copy(outputArr, 0, arr, 0, n);}/// <summary>/// 支持负数的基数排序（通过"加偏移量"将负数转为非负）/// </summary>public static void RadixSortWithNegative(int[] arr, bool isAscending = true){if (arr == null || arr.Length <= 1) return;//找到最小负数，计算偏移量（让所有数转为非负：num + offset ≥ 0）int minNum = arr[0];foreach (int num in arr){if (num < minNum)minNum = num;}int offset = minNum < 0 ? -minNum : 0;//若有负数，偏移量为"最小负数的绝对值"//1.所有数加偏移量，转为非负for (int i = 0; i < arr.Length; i++){arr[i] += offset;}//2.执行普通基数排序RadixSort(arr, isAscending);//3.减去偏移量，恢复原数值for (int i = 0; i < arr.Length; i++){arr[i] -= offset;}}/// <summary>/// 桶排序/// </summary>/// <param name="arr">待排序数组（支持int、long、float、double）</param>/// <param name="bucketCount">桶数量（默认10，可根据数据分布调整）</param>/// <param name="isAscending">排序方向：true=升序，false=降序</param>public static void BucketSort<T>(T[] arr, int bucketCount = 10, bool isAscending = true) where T : IComparable<T>{//输入校验if (arr == null || arr.Length <= 1 || bucketCount <= 0) return;//1.确定数据范围（最大值和最小值）T min = arr[0];T max = arr[0];foreach (var item in arr){if (item.CompareTo(min) < 0) min = item;if (item.CompareTo(max) > 0) max = item;}//2.创建桶（用链表或列表存储，此处用List<T>）List<T>[] buckets = new List<T>[bucketCount];for (int i = 0; i < bucketCount; i++){buckets[i] = new List<T>();}//3.将元素分配到对应桶中（根据值的范围计算桶索引）foreach (var item in arr){//计算桶索引：将[min, max]映射到[0, bucketCount-1]int bucketIndex = CalculateBucketIndex(item, min, max, bucketCount);buckets[bucketIndex].Add(item);}//4.对每个桶单独排序（此处复用系统排序，也可替换为其他排序如插入排序）foreach (var bucket in buckets){//bucket.Sort();//系统排序默认升序，为非稳定排序//if (!isAscending)//{//    bucket.Reverse();//降序时反转桶内元素//}//最常用插入排序T[] arrTest = bucket.ToArray();if (isAscending)InsertionSort(arrTest);elseInsertionSort(arrTest, false);bucket.Clear();bucket.AddRange(arrTest);}//5.合并所有桶的元素到原数组int arrIndex = 0;foreach (var bucket in buckets){foreach (var item in bucket){arr[arrIndex++] = item;}}}/// <summary>/// 计算元素应放入的桶索引/// </summary>private static int CalculateBucketIndex<T>(T item, T min, T max, int bucketCount) where T : IComparable<T>{//处理数值类型（int/long/float/double）if (typeof(T) == typeof(int)){int itemInt = Convert.ToInt32(item);int minInt = Convert.ToInt32(min);int maxInt = Convert.ToInt32(max);if (maxInt == minInt) return 0;//所有元素相等时放入第0桶return (int)((itemInt - minInt) * (bucketCount - 1) / (double)(maxInt - minInt));}else if (typeof(T) == typeof(long)){long itemLong = Convert.ToInt64(item);long minLong = Convert.ToInt64(min);long maxLong = Convert.ToInt64(max);if (maxLong == minLong) return 0;return (int)((itemLong - minLong) * (bucketCount - 1) / (double)(maxLong - minLong));}else if (typeof(T) == typeof(float) || typeof(T) == typeof(double)){double itemDouble = Convert.ToDouble(item);double minDouble = Convert.ToDouble(min);double maxDouble = Convert.ToDouble(max);if (maxDouble == minDouble) return 0;return (int)((itemDouble - minDouble) * (bucketCount - 1) / (maxDouble - minDouble));}else{throw new ArgumentException("桶排序仅支持数值类型（int/long/float/double）");}}/// <summary>/// 打印数组内容/// </summary>/// <param name="arr">需打印的数组</param>/// <param name="prefix">前缀说明</param>public static void PrintArray<T>(T[] arr, string prefix = "数组内容：") where T : IComparable<T>{if (arr == null){Debug.Log($"{prefix} null");return;}Debug.Log($"{prefix} [{string.Join(", ", arr)}]");}
}

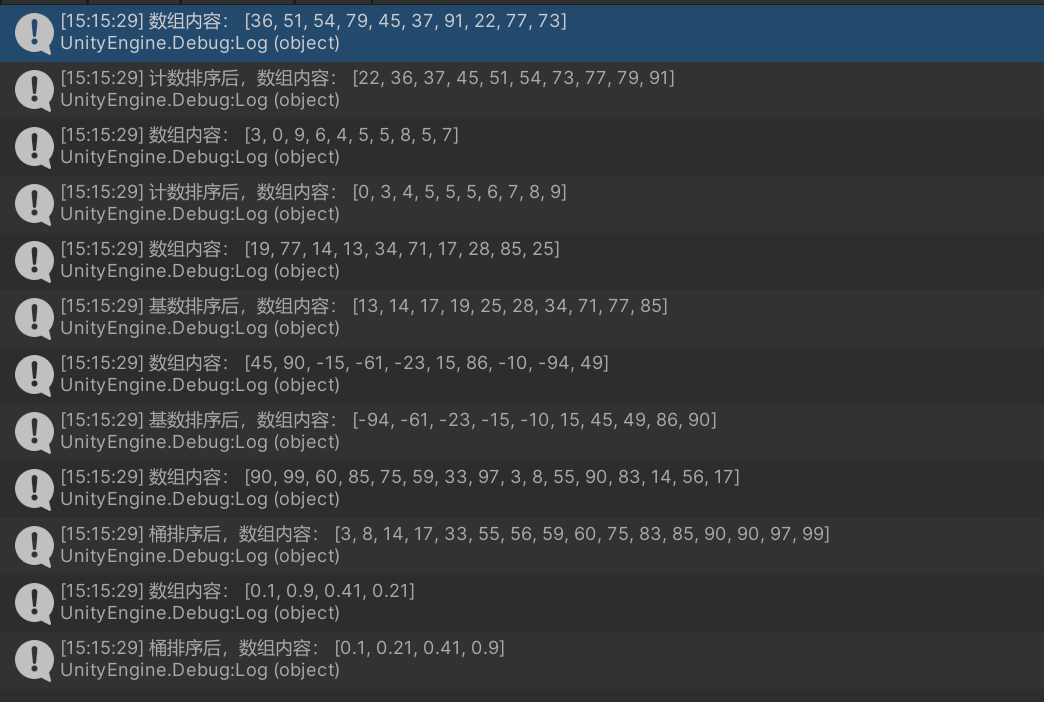
4.2.测试结果

5.总结

对比维度	计数排序（CountingSort）	基数排序（RadixSort）	桶排序（BucketSort）
核心逻辑	①统计每个元素出现次数；②计算元素在有序数组中的位置；③按位置填充元素，生成有序数组	①确定排序层级：找到数组中最大数，确定最大位数；②按位排序：按"个位→十位→百位..."依次排序；③传递有序性：逐步放大排序粒度，最终有序	①分桶，确定数据范围，创建桶；根据数据值计算“桶索引”，将每个元素放入对应的桶中；②桶内排序：对每个非空桶单独排序；③合并桶
时间复杂度	平均/最好/最坏：O(n+k)（n=数组长度，k=数据范围，与数据范围 k 强相关，k 越小效率越高）	平均/最好/最坏：O(d*(n+k))（d=最大位数，n=数组长度，k=单一位数范围(0~9)，实际近似O(n)，d 越小效率越高）	平均/理想情况：O(n)（数据均匀分布时）最坏：O(n²)（数据集中在一个桶，且桶内用低效排序）（依赖数据分布和桶数量）
空间复杂度	O(n+k)（n=数组长度，k=数据范围，需计数数组和输出数组）	O(n+k)（需存储计数数组和临时结果数组）	O(n+k)（k 为桶数量，需存储桶和结果数组）
稳定性	稳定（倒序遍历填充元素，相同元素按原数组顺序保留）	稳定（依赖计数排序的稳定性，相同位数的元素保留原顺序）	稳定：若桶内用稳定排序，插入排序（小规模）和归并排序（中规模）不稳定：若桶内用不稳定排序，如快速排序
适用场景	1.数据为小范围整数（如成绩 0~100、年龄 0~150）； 2.需稳定排序且空间充足。	1. 多位数整数（如手机号、身份证号）； 2.固定长度的字符串（如银行卡号）； 3.数据范围大但位数少的场景。	1. 分布均匀的数值（如 [0,1) 随机浮点数、身高 150~200cm）； 2.外部排序（数据太大无法载入内存）； 3.浮点数或大范围整数（分布均匀时）。

核心差异总结

1）数据类型依赖

计数排序仅限小范围整数；

基数排序仅限多位数整数或固定长度字符串；

桶排序支持均匀分布的数值（整数/浮点数）。

3）性能关键因素

计数排序看数据范围k（k越小越好）；

基数排序看最大位数d（d越小越好）；

桶排序看数据分布均匀性（越均匀越好）。

3）适用优先级

小范围整数→计数排序（最简单高效）；

多位数/固定长度字符串→基数排序（稳定且接近线性）；

均匀分布数值→桶排序（灵活且理论最优）。