分治思想之快排优化：三分区防退化与剪枝降复杂度

摘要

对于分治，相信大家都不陌生，在数据结构精讲中的排序算法----快排和归并都运用到了这个思想，就是把一个大问题划分为相同或者相似的小问题，通过快速解决小问题从而达到解决大问题

分治策略通常分为三个阶段：

1. 分解（Divide）：将原问题拆分成若干个规模较小、结构与原问题相似的子问题；
2. 解决（Conquer）：递归求解子问题（若子问题规模足够小，则直接求解）；
3. 合并（Combine）：将子问题的解合并为原问题的解。

这里由于leetcode的传统快排解决的时候数据可能会超时，此篇先复习快排，然后优化快排

对于优选算法第一篇中有个移动0其实就是运用了快排的思想，但是如果是移动0来完成快排的话可能会超时，因为数组仅仅被你划分成两部分（快排的时间复杂度为O(nlogn)，但是如果有重复元素的话使用移动0的思想来划分数组时间复杂度会退化，因为你如果是重复元素的话，选择key的时候，划分完，所有的元素都相等，所以会跑到key的左边，然后数据全都在左边，又在数组中选key，所以依次循环下来时间复杂度为O(N^2)，所以在leetcode一些特例当中是跑不过的，所以要有别的算法来优化一下）

声明：如果对快排不了解的可以去我的数据结构精讲当中了解一下排序算法

例题讲解

leetcode75颜色分类

通过这道题预先了解数组划分的思想，方便后续实现快排，这里的数组划分是分成了三块

算法原理讲解：

借用移动0的思想，可以采用三指针，即left right i指针，left标记左边区间  【0，left】的区域全是0

right标记右区间【right，n-1】全是2，自然中间【left+1，right-1】都是1，i指针就是遍历数组

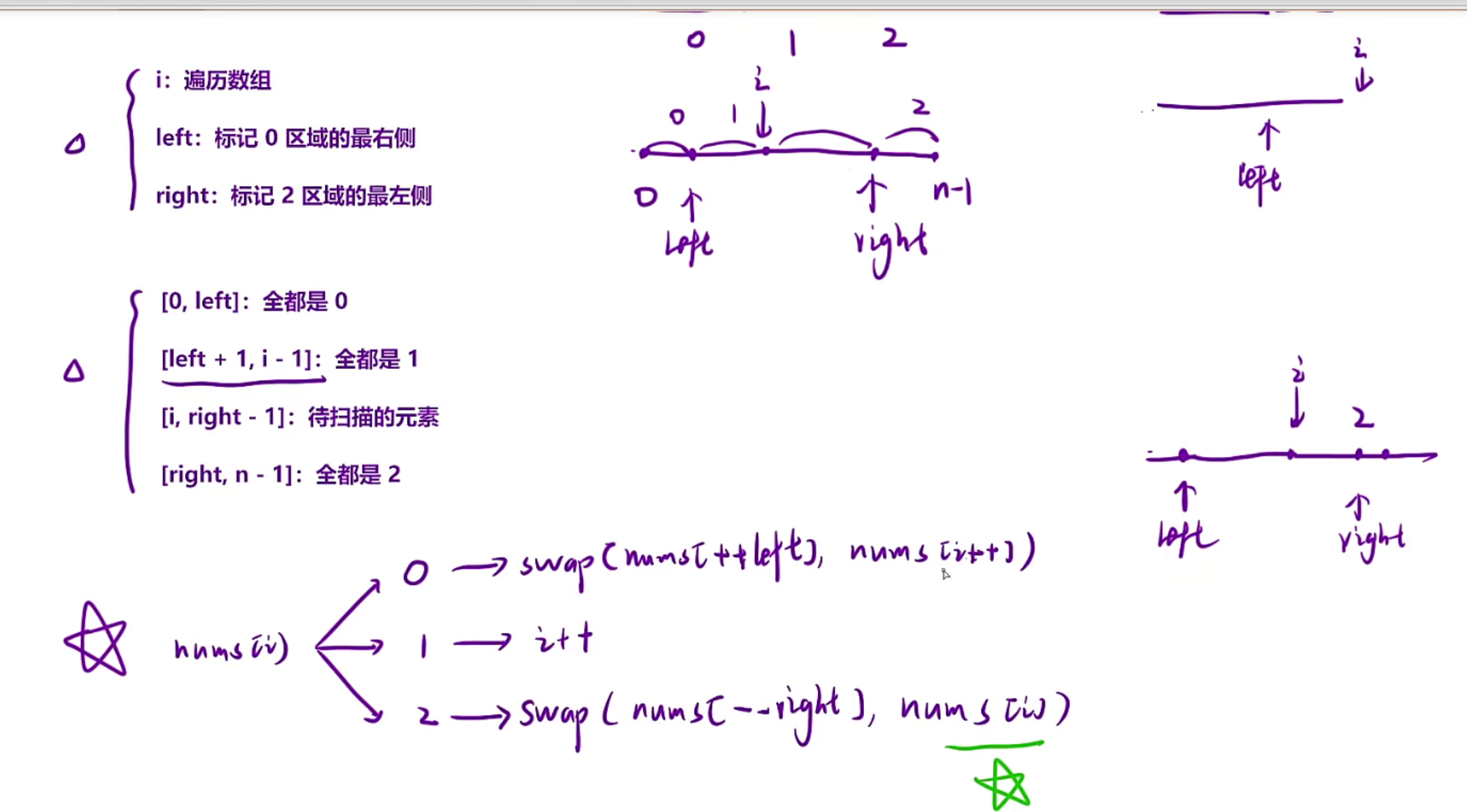
细节问题

如果nums[i]==2，那此时是和--right进行交换，此时i不需要++，因为交换完之后，i位置的元素没有进行检查过

代码

class Solution {
public:void sortColors(vector<int>& nums) {int n=nums.size();int i=0,left=-1,right=n;while(i<right){if(nums[i]==0){swap(nums[++left],nums[i++]);}else if(nums[i]==1){i++;}else{swap(nums[--right],nums[i]);}}}
};

leetcode912排序数组

通过75例题的数组划分的思想来实现快排

算法原理讲解

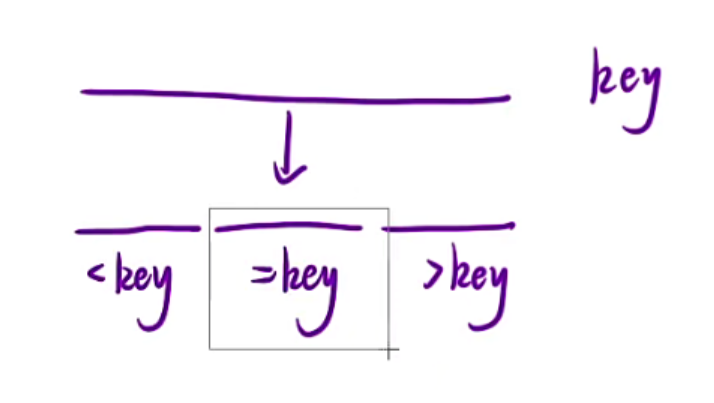
这里是使用三指针划分成三块，如果你是移动0那里就是划分成两快，左边<=key，右边>key，所以会导致如果是相同元素的话时间复杂度会退化，为什么使用三指针不会退化，原因就在于我们中间相等的区域是不会进行递归的，只递归左边和右边而已，所以如果你全都是相等元素，我左右两边区间递归进去直接就return了，此时时间复杂度仅仅为O(n)

选择一个key，然后划分成三部分区间，然后再依次递归左区间右区间即可

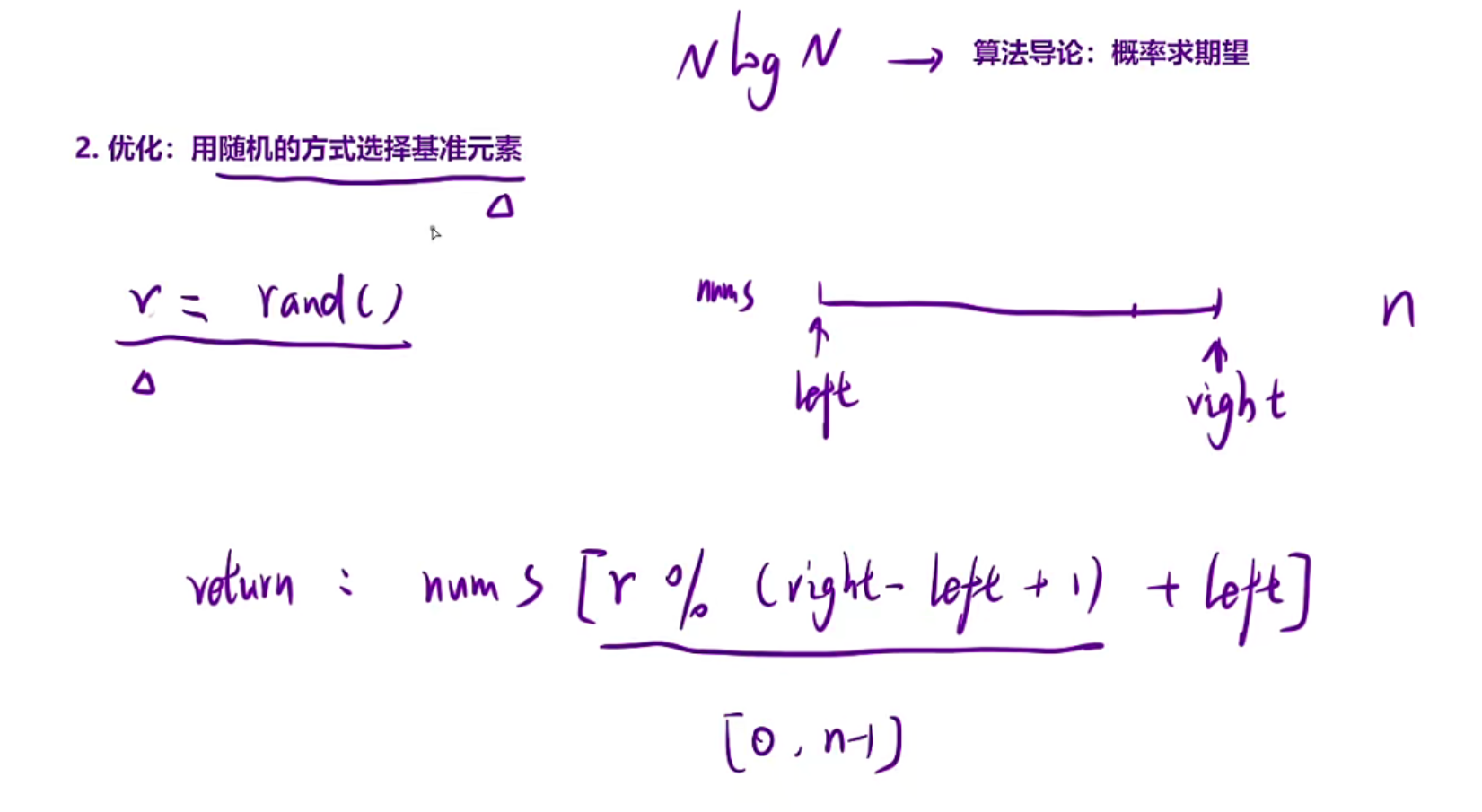
代码实现

class Solution {
public:// 生成 [l, r] 范围内的随机索引int randnumber(int l, int r) {return rand() % (r - l + 1) + l; // 正确生成 [l, r] 区间的随机索引}void sort(vector<int>& tmp, int l, int r) {if (l >= r)return;int key = tmp[randnumber(l, r)];int left = l - 1,i=l, right = r + 1;while (i < right) {if (tmp[i] < key) {swap(tmp[++left], tmp[i++]);} else if (tmp[i] == key) {i++;} else {swap(tmp[--right], tmp[i]);}}sort(tmp, l, left);sort(tmp, right, r);}vector<int> sortArray(vector<int>& nums) {// 先选择一个基准值，然后小于基准值的在区间左边，大于在右边// 随机选择基准值法srand(time(0));int n = nums.size();sort(nums, 0, n - 1);return nums;}
};

leetcode215数组中的第K个最大元素

很明显topK问题再堆排序那里我们是学过的，但是这道题要求时间复杂度为O(N)，对于我们熟知的算法，基本上是没有O(n)时间复杂度的算法，那此时就需要对排序算法进行优化

算法原理讲解

这里我们选择优化快排，对于快排前面几道题我们学过划分数组，采用划分数组+随机选择基准值的方法，这里的优化方案就是：在传统的快排当中我们需要递归左右两部分区间，这里仅仅需要判断一下第k大的元素可能在哪个区间，然后递归某一部分即可

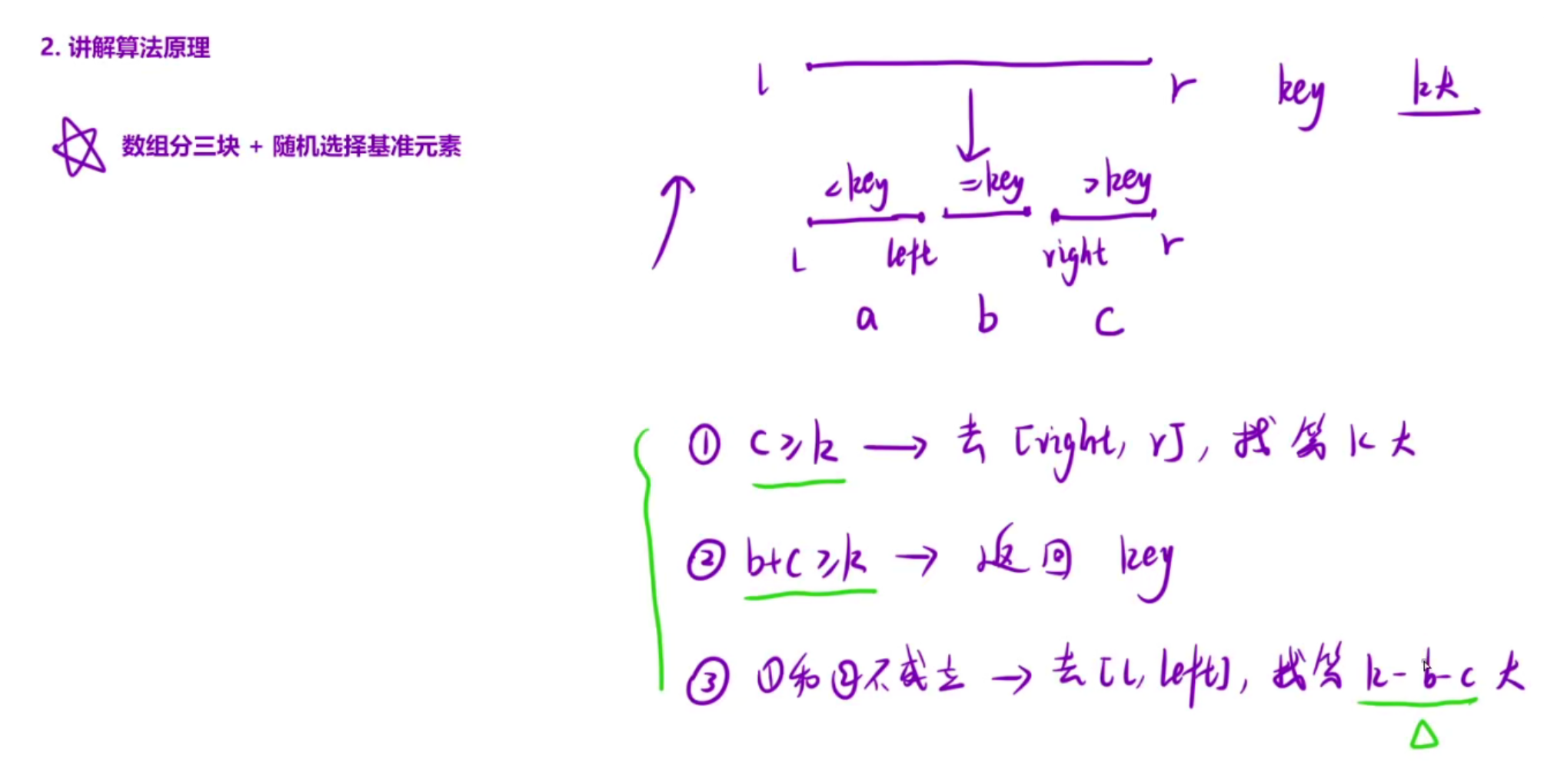
代码

class Solution {
public:// 生成 [l, r] 范围内的随机索引int randnumber(int l, int r) {return rand() % (r - l + 1) + l; // 正确生成 [l, r] 区间的随机索引}int sort(vector<int>& tmp, int l, int r, int k) {if (l >= r)return tmp[l];int key = tmp[randnumber(l, r)];int left = l - 1, i = l, right = r + 1;while (i < right) {if (tmp[i] < key) {swap(tmp[++left], tmp[i++]);} else if (tmp[i] == key) {i++;} else {swap(tmp[--right], tmp[i]);}}// 此时已经划分好数组了if (r - right+1>= k) {return sort(tmp, right, r, k);} else if (r-left>= k) {return key;} else {return sort(tmp, l, left, k-r+left);}}int findKthLargest(vector<int>& nums, int k) {srand(time(NULL));int n = nums.size();return sort(nums, 0, n - 1, k);}
};

leetcode面试题17.14.最小的k个数

算法原理讲解：

1.直接排序+选数即可 时间复杂度O(nlogn)

2.堆 构建一个k个数的大堆  时间复杂度O(nlogK)

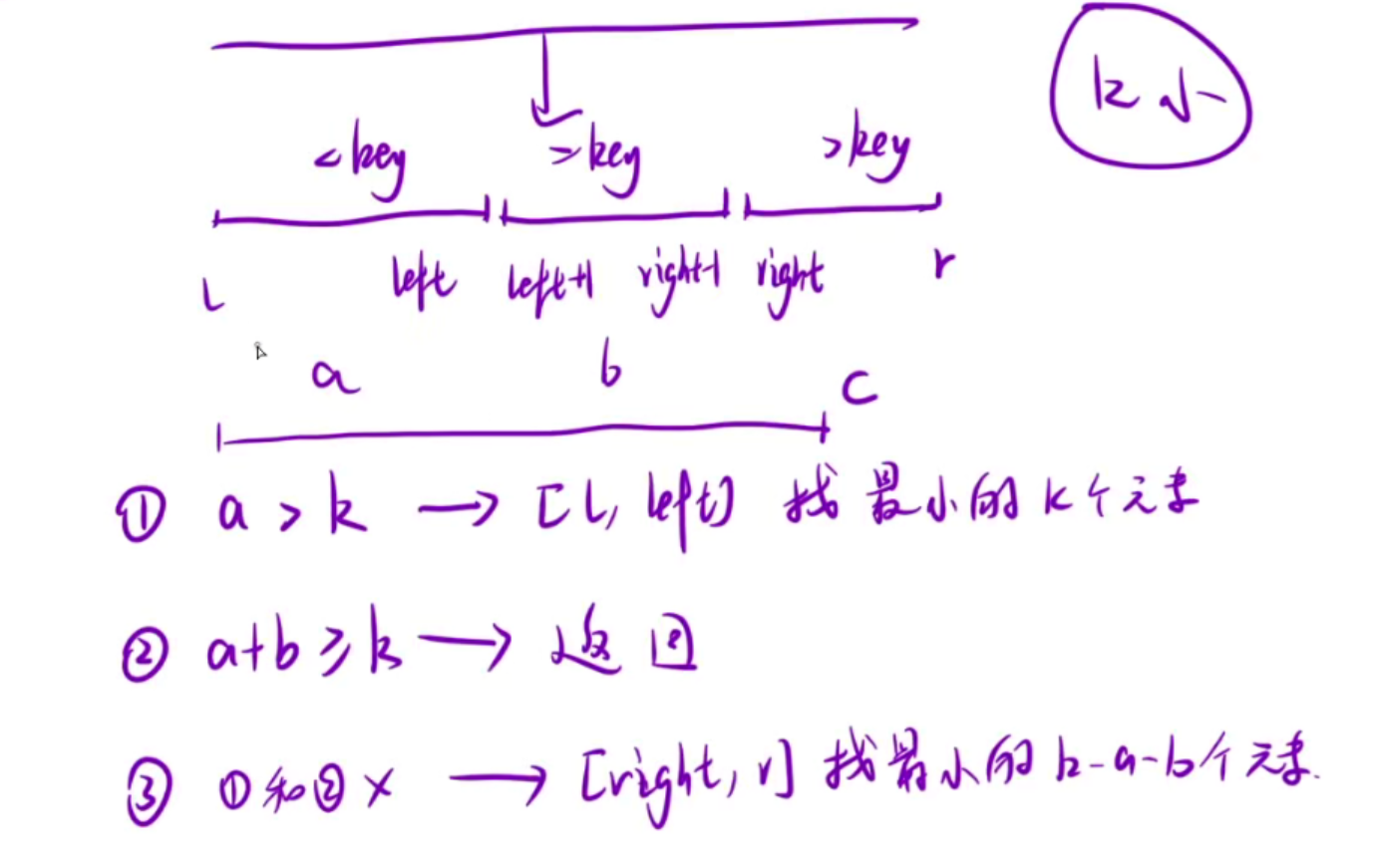
3.优化版-剪枝版快排   时间复杂度O(n)

代码

class Solution {
public:// 生成 [l, r] 范围内的随机索引int randnumber(int l, int r) {return rand() % (r - l + 1) + l; // 正确生成 [l, r] 区间的随机索引}void sort(vector<int>& tmp, int l, int r, int k) {if (l >= r)return ;int key = tmp[randnumber(l, r)];int left = l - 1, i = l, right = r + 1;while (i < right) {if (tmp[i] < key) {swap(tmp[++left], tmp[i++]);} else if (tmp[i] == key) {i++;} else {swap(tmp[--right], tmp[i]);}}// 此时已经划分好数组了,升序int a=left-l+1;int b=right-1-left;if (a>= k) {sort(tmp,l,left,k);} else if (a+b >= k) {return ;} else {sort(tmp, right, r, k - a - b);}}vector<int> smallestK(vector<int>& arr, int k) {srand(time(NULL));int n=arr.size();sort(arr,0,n-1,k);return {arr.begin(),arr.begin()+k};}
};

总结

本篇主要是讲解分治的思想，通过快排来理解，快排的时间复杂度是O(nlogn)，主要区分是分为三部分还是两部分（两部分时间复杂度可能会退化），在利用剪枝的思想去优化快排，不是递归左右区间，而是选择某一区间进行递归，时间复杂度变为O(N)，具体的推导过程需要查看算法导论

1. 三分区是快排防退化的关键：无论排序还是 TopK 问题，三分区能高效处理重复元素，是 leetcode 避免超时的核心。
2. 剪枝递归实现 O (n) 时间复杂度：TopK 类问题（第 K 大 / 最小 k 个）无需完整排序，通过判断目标元素所在区间，仅递归单个子问题，总时间复杂度从 O (nlogn) 优化至 O (n)。
3. 通用工具函数：随机生成 [l, r] 区间索引（rand()%(r-l+1)+l），需在入口函数中初始化一次种子（srand(time(0))），避免重复初始化导致随机数失效。