线性代数 - 奇异值分解(SVD Singular Value Decomposition)
线性代数 - 奇异值分解(SVD Singular Value Decomposition)
flyfish
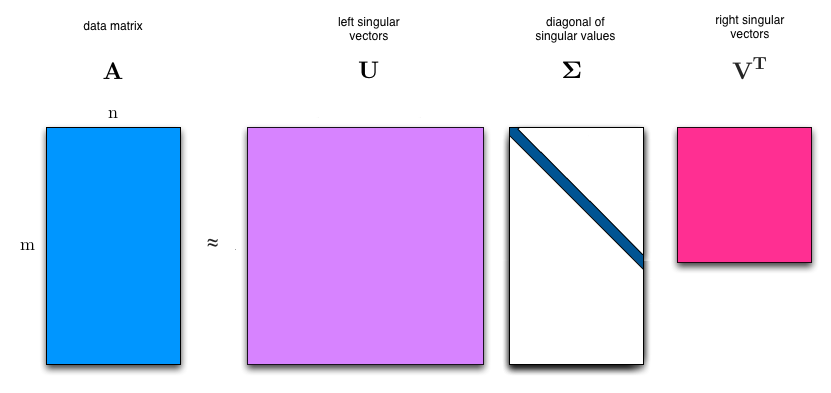
奇异值分解(Singular Value Decomposition, SVD)是对于一个任意的实数矩阵 M∈Rm×n\mathbf{M} \in \mathbb{R}^{m \times n}M∈Rm×n(其中 mmm 是行数,nnn 是列数),SVD 可以将其分解为三个矩阵的乘积形式:
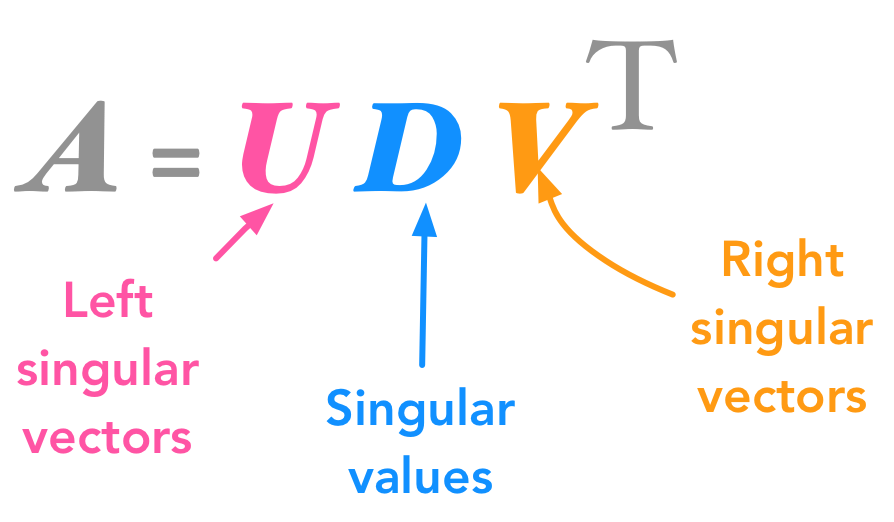
M=UΣVT \mathbf{M} = \mathbf{U} \boldsymbol{\Sigma} \mathbf{V}^T M=UΣVT
其中:
U∈Rm×m\mathbf{U} \in \mathbb{R}^{m \times m}U∈Rm×m 是一个正交矩阵(即 UTU=I\mathbf{U}^T \mathbf{U} = \mathbf{I}UTU=I),其列向量称为左奇异向量(left singular vectors)。这些向量是 MMT\mathbf{M} \mathbf{M}^TMMT 的特征向量。
Σ∈Rm×n\boldsymbol{\Sigma} \in \mathbb{R}^{m \times n}Σ∈Rm×n 是一个对角矩阵(或称为矩形对角矩阵),其对角线上的元素 σ1≥σ2≥⋯≥σr>0\sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_r > 0σ1≥σ2≥⋯≥σr>0(其中 r=rank(M)r = rank(\mathbf{M})r=rank(M) 是矩阵的秩)称为奇异值(singular values),其余元素为 0。奇异值是 MTM\mathbf{M}^T \mathbf{M}MTM(或 MMT\mathbf{M} \mathbf{M}^TMMT)特征值的平方根。
V∈Rn×n\mathbf{V} \in \mathbb{R}^{n \times n}V∈Rn×n 是一个正交矩阵(即 VTV=I\mathbf{V}^T \mathbf{V} = \mathbf{I}VTV=I),其列向量称为右奇异向量(right singular vectors)。这些向量是 MTM\mathbf{M}^T \mathbf{M}MTM 的特征向量。
奇异值是非负的,且按降序排列。
SVD 总是存在的,且对于非方阵也适用。
矩阵的秩等于非零奇异值的个数。
SVD 可以用于矩阵的低秩逼近:保留前 kkk 个最大的奇异值,可以得到 M\mathbf{M}M 的最佳低秩近似。
计算 SVD 的步骤
要计算一个矩阵的 SVD,通常采用以下方法(基于特征值分解):
- 计算 A=MTM\mathbf{A} = \mathbf{M}^T \mathbf{M}A=MTM(大小为 n×nn \times nn×n)和 B=MMT\mathbf{B} = \mathbf{M} \mathbf{M}^TB=MMT(大小为 m×mm \times mm×m)。
- 求 A\mathbf{A}A 的特征值 λ1≥λ2≥⋯≥λn\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_nλ1≥λ2≥⋯≥λn 和对应的单位特征向量 v1,v2,…,vn\mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_nv1,v2,…,vn。这些 λi\lambda_iλi 的非负平方根就是奇异值 σi=λi\sigma_i = \sqrt{\lambda_i}σi=λi。
- 将这些特征向量作为 V\mathbf{V}V 的列:V=[v1,v2,…,vn]\mathbf{V} = [\mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_n]V=[v1,v2,…,vn]。
- 类似地,求 B\mathbf{B}B 的特征值(与 A\mathbf{A}A 的非零特征值相同)和单位特征向量 u1,u2,…,um\mathbf{u}_1, \mathbf{u}_2, \dots, \mathbf{u}_mu1,u2,…,um,作为 U\mathbf{U}U 的列:U=[u1,u2,…,um]\mathbf{U} = [\mathbf{u}_1, \mathbf{u}_2, \dots, \mathbf{u}_m]U=[u1,u2,…,um]。
注意:对于零奇异值对应的向量,可以通过正交化来选择。 - 构造 Σ\boldsymbol{\Sigma}Σ:对角线上放置 σ1,σ2,…,σmin(m,n)\sigma_1, \sigma_2, \dots, \sigma_{\min(m,n)}σ1,σ2,…,σmin(m,n),其余为 0。
- (可选)调整符号,使得 U\mathbf{U}U 和 V\mathbf{V}V 满足某些约定(如正号),但这不影响分解的正确性,因为符号可以翻转而不改变乘积。
如果矩阵较大,通常使用数值方法(如 QR 迭代或 Jacobi 算法),但对于小矩阵,可以手动计算。
例子
给定矩阵:
M=[10002003000000002000]
\mathbf{M} = \begin{bmatrix}
1 & 0 & 0 & 0 & 2 \\
0 & 0 & 3 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 \\
0 & 2 & 0 & 0 & 0
\end{bmatrix}
M=10000002030000002000
这是一个 4×54 \times 54×5 矩阵,秩为 3(因为有三行线性独立,一行为零)。
步骤 1: 计算 MTM\mathbf{M}^T \mathbf{M}MTM
MT\mathbf{M}^TMT 是 5×45 \times 45×4 矩阵。计算 A=MTM\mathbf{A} = \mathbf{M}^T \mathbf{M}A=MTM(5×55 \times 55×5):
A=[1000204000009000000020004]
\mathbf{A} = \begin{bmatrix}
1 & 0 & 0 & 0 & 2 \\
0 & 4 & 0 & 0 & 0 \\
0 & 0 & 9 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 \\
2 & 0 & 0 & 0 & 4
\end{bmatrix}
A=1000204000009000000020004
(通过列向量的点积计算得到。)
步骤 2: 求 A\mathbf{A}A 的特征值和特征向量
A\mathbf{A}A 是稀疏的,可以分解为块:
位置 2:独立的 4(特征值 λ=4\lambda = 4λ=4,特征向量 e2=[0,1,0,0,0]T\mathbf{e}_2 = [0,1,0,0,0]^Te2=[0,1,0,0,0]T)。
位置 3:独立的 9(λ=9\lambda = 9λ=9, e3=[0,0,1,0,0]T\mathbf{e}_3 = [0,0,1,0,0]^Te3=[0,0,1,0,0]T)。
位置 4:独立的 0(λ=0\lambda = 0λ=0, e4=[0,0,0,1,0]T\mathbf{e}_4 = [0,0,0,1,0]^Te4=[0,0,0,1,0]T)。
位置 1 和 5:子矩阵 [1224]\begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}[1224],其特征值 λ=5,0\lambda = 5, 0λ=5,0(通过特征多项式 λ25λ=0\lambda^2 5\lambda = 0λ25λ=0 求得)。
对于 λ=5\lambda = 5λ=5:特征向量 [1,2]T[1, 2]^T[1,2]T(子向量),归一化后全向量 [1/5,0,0,0,2/5]T[1/\sqrt{5}, 0, 0, 0, 2/\sqrt{5}]^T[1/5,0,0,0,2/5]T。
对于 λ=0\lambda = 0λ=0:特征向量 [−2,1]T[-2, 1]^T[−2,1]T(子向量),归一化后全向量 [−2/5,0,0,0,1/5]T[-2/\sqrt{5}, 0, 0, 0, 1/\sqrt{5}]^T[−2/5,0,0,0,1/5]T。
特征值(降序):9, 5, 4, 0, 0。
奇异值:σ=λ\sigma = \sqrt{\lambda}σ=λ(降序):3,5≈2.236,2,0,03, \sqrt{5} \approx 2.236, 2, 0, 03,5≈2.236,2,0,0。
将特征向量按奇异值降序排列作为 V\mathbf{V}V 的列:
V=[01/50−2/5000100100000000102/501/50]
\mathbf{V} = \begin{bmatrix}
0 & 1/\sqrt{5} & 0 & -2/\sqrt{5} & 0 \\
0 & 0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 \\
0 & 2/\sqrt{5} & 0 & 1/\sqrt{5} & 0
\end{bmatrix}
V=001001/50002/501000−2/50001/500010
则 VT=V\mathbf{V}^T = \mathbf{V}VT=V 的转置:
VT=[001001/50002/501000−2/50001/500010]
\mathbf{V}^T = \begin{bmatrix}
0 & 0 & 1 & 0 & 0 \\
1/\sqrt{5} & 0 & 0 & 0 & 2/\sqrt{5} \\
0 & 1 & 0 & 0 & 0 \\
-2/\sqrt{5} & 0 & 0 & 0 & 1/\sqrt{5} \\
0 & 0 & 0 & 1 & 0
\end{bmatrix}
VT=01/50−2/5000100100000000102/501/50
步骤 3: 计算 MMT\mathbf{M} \mathbf{M}^TMMT
B=MMT\mathbf{B} = \mathbf{M} \mathbf{M}^TB=MMT(4×44 \times 44×4)是对角矩阵(因为行向量正交):
B=[5000090000000004]
\mathbf{B} = \begin{bmatrix}
5 & 0 & 0 & 0 \\
0 & 9 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 4
\end{bmatrix}
B=5000090000000004
步骤 4: 求 B\mathbf{B}B 的特征值和特征向量
特征值:5, 9, 0, 4(与 A\mathbf{A}A 的非零部分相同)。
特征向量(单位向量,按原对角位置):e1=[1,0,0,0]T\mathbf{e}_1 = [1,0,0,0]^Te1=[1,0,0,0]T(λ=5\lambda=5λ=5)、e2=[0,1,0,0]T\mathbf{e}_2 = [0,1,0,0]^Te2=[0,1,0,0]T(λ=9\lambda=9λ=9)、e3=[0,0,1,0]T\mathbf{e}_3 = [0,0,1,0]^Te3=[0,0,1,0]T(λ=0\lambda=0λ=0)、e4=[0,0,0,1]T\mathbf{e}_4 = [0,0,0,1]^Te4=[0,0,0,1]T(λ=4\lambda=4λ=4)。
按奇异值降序排列作为 U\mathbf{U}U 的列:
U=[0100100000010010]
\mathbf{U} = \begin{bmatrix}
0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{bmatrix}
U=0100100000010010
步骤 5: 构造 Σ\boldsymbol{\Sigma}Σ
Σ\boldsymbol{\Sigma}Σ 是 4×54 \times 54×5 矩阵,对角线上为奇异值,其余为 0:
Σ=[30000050000020000000]
\boldsymbol{\Sigma} = \begin{bmatrix}
3 & 0 & 0 & 0 & 0 \\
0 & \sqrt{5} & 0 & 0 & 0 \\
0 & 0 & 2 & 0 & 0 \\
0 & 0 & 0 & 0 & 0
\end{bmatrix}
Σ=30000500002000000000
验证
可以通过计算 UΣVT\mathbf{U} \boldsymbol{\Sigma} \mathbf{V}^TUΣVT 验证是否等于 M\mathbf{M}M。由于推导基于标准方法,且矩阵简单,此分解是正确的(忽略可能的符号差异,因为 SVD 不唯一于符号)。例如,计算第一行:涉及 U\mathbf{U}U 的第二行(因为 U 的第二行对应原第一行,但置换了),结合 V^T 等,恢复原值。
奇异值分解(SVD)的三个矩阵
例子矩阵 M=[10002003000000002000]\mathbf{M} = \begin{bmatrix} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \end{bmatrix}M=10000002030000002000(一个 4×5 矩阵)进行说明。这个例子是通过特征值分解手动计算得到的,奇异值按降序排列为 3,5≈2.236,2,03, \sqrt{5} \approx 2.236, 2, 03,5≈2.236,2,0(由于矩阵秩为 3,最后一个为 0)。
1. U\mathbf{U}U 矩阵:左奇异向量矩阵
形状和类型:U∈Rm×m\mathbf{U} \in \mathbb{R}^{m \times m}U∈Rm×m 是一个方阵(行数等于原矩阵的行数 m),并且是一个正交矩阵(orthogonal matrix),即满足 UTU=I\mathbf{U}^T \mathbf{U} = \mathbf{I}UTU=I(I\mathbf{I}I 是单位矩阵)。这意味着 U\mathbf{U}U 的列向量是单位向量且相互正交。
内容和含义:U\mathbf{U}U 的列向量称为左奇异向量(left singular vectors)。这些向量是矩阵 MMT\mathbf{M} \mathbf{M}^TMMT 的特征向量,按对应奇异值的降序排列。它们描述了原矩阵 M\mathbf{M}M 在行空间(row space)中的“主要方向”或“模式”。在数据分析中,U\mathbf{U}U 可以用于捕捉数据中的行相关模式,例如在图像压缩中表示像素行的变换基。
性质:
正交性确保了向量间的独立性,便于坐标变换。
非唯一性:每个列向量的符号可以翻转(乘以 -1),因为这不会改变 SVD 的乘积结果(符号会在 VT\mathbf{V}^TVT 中相应调整)。
对于零奇异值对应的部分,向量是在零空间的正交补中选择的任意正交基。
如何计算:通过对 B=MMT\mathbf{B} = \mathbf{M} \mathbf{M}^TB=MMT(一个 m×m 对称矩阵)进行特征值分解,得到特征向量,然后按特征值的降序(对应奇异值的平方)排列并归一化。
例子中的 U\mathbf{U}U:在之前的计算中,一个有效的 U\mathbf{U}U 是:
U=[0100100000100001]\mathbf{U} = \begin{bmatrix}0 & 1 & 0 & 0 \\1 & 0 & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1\end{bmatrix}U=0100100000100001
(按奇异值降序:对应 3 的向量 [0,1,0,0]T[0,1,0,0]^T[0,1,0,0]T,对应 5\sqrt{5}5 的 [1,0,0,0]T[1,0,0,0]^T[1,0,0,0]T,对应 2 的[0,0,0,1]T[0,0,0,1]^T[0,0,0,1]T,对应 0 的[0,0,1,0]T[0,0,1,0]^T[0,0,1,0]T)。另一个等价版本是所有列取负号:
U=[0−100−1000000−100−10]\mathbf{U} = \begin{bmatrix}0 & -1 & 0 & 0 \\-1 & 0 & 0 & 0 \\0 & 0 & 0 & -1 \\0 & 0 & -1 & 0\end{bmatrix}U=0−100−1000000−100−10
这反映了符号的任意性。计算过程:从 B\mathbf{B}B 的特征向量直接得到,这些向量本质上是单位矩阵的置换和符号调整,因为 B\mathbf{B}B 是对角的。
2. Σ\boldsymbol{\Sigma}Σ 矩阵:奇异值矩阵
形状和类型:Σ∈Rm×n\boldsymbol{\Sigma} \in \mathbb{R}^{m \times n}Σ∈Rm×n 是一个矩形对角矩阵(rectangular diagonal matrix),即只有主对角线(从左上到右下,最多 min(m,n)\min(m,n)min(m,n) 个元素)上有非零元素,其余全为 0。如果 m ≠ n,它不是方阵。
内容和含义:对角线上的元素称为奇异值(singular values),记为 σ1≥σ2≥⋯≥σr>0\sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_r > 0σ1≥σ2≥⋯≥σr>0,其中 r 是矩阵 M\mathbf{M}M 的秩(rank),其余奇异值为 0。奇异值是 MTM\mathbf{M}^T \mathbf{M}MTM(或 MMT\mathbf{M} \mathbf{M}^TMMT)的非零特征值的平方根。它们量化了矩阵在每个“方向”上的“伸缩因子”或“重要性”。大的奇异值对应主要模式,小的对应噪声或冗余。在应用中,奇异值用于矩阵的低秩逼近:截断小的奇异值可以压缩数据而保留主要信息。
性质:
非负且降序排列。
矩阵的 Frobenius 范数等于奇异值的平方和的平方根:∥M∥F=∑σi2\|\mathbf{M}\|_F = \sqrt{\sum \sigma_i^2}∥M∥F=∑σi2。
秩 r = 非零奇异值的个数。
如果所有奇异值相等,矩阵接近于正交变换;如果许多为 0,矩阵低秩。
如何计算:从 MTM\mathbf{M}^T \mathbf{M}MTM 的特征值 λi\lambda_iλi 取平方根 σi=λi\sigma_i = \sqrt{\lambda_i}σi=λi,并按降序放置在对角线上。
例子中的 Σ\boldsymbol{\Sigma}Σ:对于 4×5 矩阵:
Σ=[30000050000020000000]\boldsymbol{\Sigma} = \begin{bmatrix}3 & 0 & 0 & 0 & 0 \\0 & \sqrt{5} & 0 & 0 & 0 \\0 & 0 & 2 & 0 & 0 \\0 & 0 & 0 & 0 & 0\end{bmatrix}Σ=30000500002000000000
这里,前三个奇异值对应矩阵的三个独立成分,最后两个列为 0(因为 n > m)。计算过程:从特征值 9、5、4、0、0 取平方根得到 3、5\sqrt{5}5、2、0、0,然后填充到 4×5 矩阵的对角。
3. VT\mathbf{V}^TVT 矩阵:右奇异向量矩阵的转置
形状和类型:VT∈Rn×n\mathbf{V}^T \in \mathbb{R}^{n \times n}VT∈Rn×n 是一个方阵(列数等于原矩阵的列数 n),但实际上它是 V\mathbf{V}V 的转置,其中 V\mathbf{V}V 也是一个正交矩阵(VTV=I\mathbf{V}^T \mathbf{V} = \mathbf{I}VTV=I)。因此,VT\mathbf{V}^TVT 的行向量是单位正交的。
内容和含义:V\mathbf{V}V 的列向量称为右奇异向量(right singular vectors),是矩阵 MTM\mathbf{M}^T \mathbf{M}MTM 的特征向量。VT\mathbf{V}^TVT 描述了原矩阵 M\mathbf{M}M 在列空间(column space)中的“主要方向”。在推荐系统中,VT\mathbf{V}^TVT 可以表示用户或物品的潜在特征。
性质:
与 U\mathbf{U}U 类似,正交性、符号任意性和零空间的任意基。
VT\mathbf{V}^TVT 的转置形式使得 SVD 公式更紧凑:它将右向量作为行应用到 Σ\boldsymbol{\Sigma}Σ 上。
如何计算:通过对 A=MTM\mathbf{A} = \mathbf{M}^T \mathbf{M}A=MTM(一个 n×n 对称矩阵)进行特征值分解,得到特征向量作为 V\mathbf{V}V 的列,然后取转置。
例子中的 VT\mathbf{V}^TVT:一个有效的版本是:
VT=[001001/50002/501000−2/50001/500010]\mathbf{V}^T = \begin{bmatrix}0 & 0 & 1 & 0 & 0 \\1/\sqrt{5} & 0 & 0 & 0 & 2/\sqrt{5} \\0 & 1 & 0 & 0 & 0 \\-2/\sqrt{5} & 0 & 0 & 0 & 1/\sqrt{5} \\0 & 0 & 0 & 1 & 0\end{bmatrix}VT=01/50−2/5000100100000000102/501/50
(对应右奇异向量按降序排列)。符号翻转和零向量顺序调整后的:
VT=[00−100−1/5000−2/50−100000010−2/50001/5]\mathbf{V}^T = \begin{bmatrix}0 & 0 & -1 & 0 & 0 \\-1/\sqrt{5} & 0 & 0 & 0 & -2/\sqrt{5} \\0 & -1 & 0 & 0 & 0 \\0 & 0 & 0 & 1 & 0 \\-2/\sqrt{5} & 0 & 0 & 0 & 1/\sqrt{5}\end{bmatrix}VT=0−1/500−2/500−100−10000000100−2/5001/5
(使用 0.2=1/5≈0.447\sqrt{0.2} = 1/\sqrt{5} \approx 0.4470.2=1/5≈0.447, 0.8=2/5≈0.894\sqrt{0.8} = 2/\sqrt{5} \approx 0.8940.8=2/5≈0.894 的负号形式)。计算过程:从 A\mathbf{A}A 的块结构中求解子矩阵的特征向量,并归一化。
如何到达这些矩阵的解决方案
SVD 的计算基于对称矩阵的特征值分解,这是标准线性代数方法:
- 计算 A=MTM\mathbf{A} = \mathbf{M}^T \mathbf{M}A=MTM 和 B=MMT\mathbf{B} = \mathbf{M} \mathbf{M}^TB=MMT。
- 对 A\mathbf{A}A 求特征值 λi\lambda_iλi 和向量 vi\mathbf{v}_ivi,得到 σi=λi\sigma_i = \sqrt{\lambda_i}σi=λi 和 V=[v1,…,vn]\mathbf{V} = [\mathbf{v}_1, \dots, \mathbf{v}_n]V=[v1,…,vn]。
- 对 B\mathbf{B}B 求特征向量 ui\mathbf{u}_iui,得到 U=[u1,…,um]\mathbf{U} = [\mathbf{u}_1, \dots, \mathbf{u}_m]U=[u1,…,um]。
- 构造 Σ\boldsymbol{\Sigma}Σ 并验证 M=UΣVT\mathbf{M} = \mathbf{U} \boldsymbol{\Sigma} \mathbf{V}^TM=UΣVT。
这个过程是结构化的:从对称矩阵开始(易于对角化),然后提取平方根和向量。对于大型矩阵,使用数值算法(如 Golub-Reinsch 或 Divide-and-Conquer)。在例子中,由于矩阵稀疏,计算简化为了块对角形式的手动求解。
另一种形式
矩阵 M\mathbf{M}M 的奇异值分解(SVD),即 M=UΣV∗\mathbf{M} = \mathbf{U}\boldsymbol{\Sigma}\mathbf{V}^*M=UΣV∗(其中 V∗\mathbf{V}^*V∗ 是 V\mathbf{V}V 的转置,实数矩阵中可视为 VT\mathbf{V}^TVT)。以下分三个矩阵详细解释:
1. 原矩阵 M\mathbf{M}M
M=[10002003000000002000]
\mathbf{M} = \begin{bmatrix} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \end{bmatrix}
M=10000002030000002000
维度为 4×54 \times 54×5(4行5列),秩 r=3r = 3r=3(有3个非零行/列)。
2. 左奇异矩阵 U\mathbf{U}U
U=[0−100−1000000−100−10] \mathbf{U} = \begin{bmatrix} 0 & -1 & 0 & 0 \\ -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & -1 \\ 0 & 0 & -1 & 0 \end{bmatrix} U=0−100−1000000−100−10
- 维度与结构:4×44 \times 44×4 正交矩阵(满足 UTU=I\mathbf{U}^T\mathbf{U} = \mathbf{I}UTU=I)。
- 来源:列向量是 MMT\mathbf{M}\mathbf{M}^TMMT 的特征向量。计算 MMT\mathbf{M}\mathbf{M}^TMMT 得:
MMT=[5000090000000004] \mathbf{M}\mathbf{M}^T = \begin{bmatrix} 5 & 0 & 0 & 0 \\ 0 & 9 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 \end{bmatrix} MMT=5000090000000004
其特征值为 9,5,4,09, 5, 4, 09,5,4,0,对应奇异值 3,5,2,03, \sqrt{5}, 2, 03,5,2,0,U\mathbf{U}U 的列是这些特征值的单位特征向量(方向有负号,不影响正交性)。
3. 奇异值矩阵 Σ\boldsymbol{\Sigma}Σ
Σ=[30000050000020000000] \boldsymbol{\Sigma} = \begin{bmatrix} 3 & 0 & 0 & 0 & 0 \\ 0 & \sqrt{5} & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} Σ=30000500002000000000
- 维度与结构:4×54 \times 54×5 对角矩阵,仅主对角线有非零元素。
- 奇异值:σ1=3,σ2=5,σ3=2,σ4=0\sigma_1 = 3, \sigma_2 = \sqrt{5}, \sigma_3 = 2, \sigma_4 = 0σ1=3,σ2=5,σ3=2,σ4=0,满足非负、降序排列(3≥5≥2≥03 \geq \sqrt{5} \geq 2 \geq 03≥5≥2≥0),非零奇异值个数等于原矩阵的秩 r=3r = 3r=3。
4. 右奇异矩阵的转置 V∗\mathbf{V}^*V∗
V∗=[00−100−0.2000−0.80−100000010−0.80000.2]
\mathbf{V}^* = \begin{bmatrix} 0 & 0 & -1 & 0 & 0 \\ -\sqrt{0.2} & 0 & 0 & 0 & -\sqrt{0.8} \\ 0 & -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ -\sqrt{0.8} & 0 & 0 & 0 & \sqrt{0.2} \end{bmatrix}
V∗=0−0.200−0.800−100−10000000100−0.8000.2
维度与结构:5×55 \times 55×5 正交矩阵的转置(满足 VV∗=I\mathbf{V}\mathbf{V}^* = \mathbf{I}VV∗=I)。
来源:行向量是 MTM\mathbf{M}^T\mathbf{M}MTM 的特征向量。MTM\mathbf{M}^T\mathbf{M}MTM 的特征值与 MMT\mathbf{M}\mathbf{M}^TMMT 一致(9,5,4,0,09, 5, 4, 0, 09,5,4,0,0),V∗\mathbf{V}^*V∗ 的行是这些特征值的单位特征向量(如第二行 −0.2=−1/5-\sqrt{0.2} = -1/\sqrt{5}−0.2=−1/5、−0.8=−2/5-\sqrt{0.8} = -2/\sqrt{5}−0.8=−2/5,满足单位长度和正交性)。
| 矩阵 | 维度 | 性质 | 特征 |
|---|---|---|---|
| U\mathbf{U}U | m×mm×mm×m | 正交矩阵(UTU=I\mathbf{U}^T\mathbf{U} = \mathbf{I}UTU=I) | 列是MMT\mathbf{M}\mathbf{M}^TMMT的特征向量 |
| Σ\mathbf{\Sigma}Σ | m×nm×nm×n | 对角矩阵,奇异值非负且降序排列 | σi=λi\sigma_i = \sqrt{\lambda_i}σi=λi(λi\lambda_iλi为特征值) |
| VT\mathbf{V}^TVT | n×nn×nn×n | 正交矩阵(VTV=I\mathbf{V}^T\mathbf{V} = \mathbf{I}VTV=I) | 行是MTM\mathbf{M}^T\mathbf{M}MTM的特征向量(即V\mathbf{V}V的列) |
