LC110 平衡二叉树

一.任务描述：

给定一个二叉树，判断它是否是 平衡二叉树  

示例 1：

 

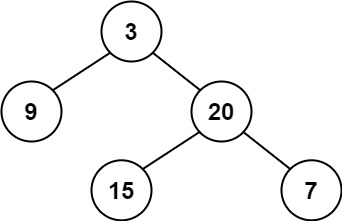
输入：root = [3,9,20,null,null,15,7]

输出：true

示例 2：

 

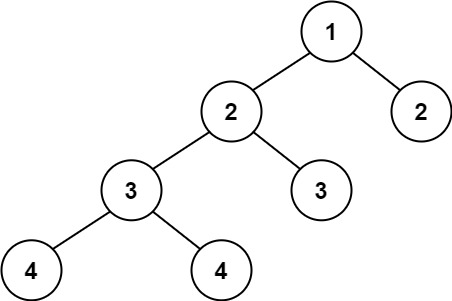
输入：root = [1,2,2,3,3,null,null,4,4]

输出：false

示例 3：

输入：root = []

输出：true

 

二.解题思路:

自底向上的递归

1. 从叶子节点开始计算高度

2. 如果子树不平衡，立即返回-1标记不平衡

3. 否则返回实际高度供父节点使用

4. 最终检查根节点是否返回-1

三.代码实现:

C

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
int checkHeight(struct TreeNode* root) {if (root == NULL) {return 0;}// 递归检查左子树高度int leftHeight = checkHeight(root->left);if (leftHeight == -1) {return -1; // 左子树不平衡，直接返回}// 递归检查右子树高度int rightHeight = checkHeight(root->right);if (rightHeight == -1) {return -1; // 右子树不平衡，直接返回}// 检查当前节点是否平衡if (abs(leftHeight - rightHeight) > 1) {return -1; // 当前节点不平衡}// 返回当前子树的高度return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
}bool isBalanced(struct TreeNode* root) {// 如果checkHeight返回-1表示不平衡，否则平衡return checkHeight(root) != -1;
}

四.总结:

核心技巧：

1. checkHeight函数：

   • 计算子树高度同时检查平衡性

   • 返回-1表示子树不平衡

   • 返回正整数表示子树高度

2. isBalanced函数：

   • 调用辅助函数检查整棵树

   • 如果返回-1则不平衡，否则平衡

3. 算法特点：

   • 时间复杂度：O(n) - 每个节点访问一次

   • 空间复杂度：O(h) - 递归栈深度，h为树高

   • 自底向上检查，避免重复计算